2.3: Граничні закони
- Page ID
- 62326
- Визнати основні граничні закони.
- Використовуйте граничні закони для оцінки межі функції.
- Оцініть ліміт функції шляхом факторингу.
- Використовуйте граничні закони для оцінки межі полінома або раціональної функції.
- Оцінити межу функції шляхом факторингу або за допомогою кон'югатів.
- Оцінити межу функції за допомогою теореми стискання.
У попередньому розділі ми оцінювали межі, подивившись на графіки або побудувавши таблицю значень. У цьому розділі ми встановлюємо закони розрахунку лімітів і дізнаємося, як застосовувати ці закони. У студентському проекті в кінці цього розділу у вас є можливість застосувати ці граничні закони, щоб вивести формулу для площі кола шляхом адаптації методу, розробленого грецьким математиком Архімедом. Ми починаємо з відновлення двох корисних результатів ліміту з попереднього розділу. Ці два результати разом з граничними законами служать основою для обчислення багатьох лімітів.
Оцінка лімітів за допомогою граничних законів
Перші два граничні закони були викладені раніше, і ми повторюємо їх тут. Ці основні результати разом з іншими граничними законами дозволяють оцінити межі багатьох алгебраїчних функцій.
Для будь-якого дійсного числа\(a\) і будь-якої константи\(c\),
- \(\displaystyle \lim_{x→a}x=a\)
- \(\displaystyle \lim_{x→a}c=c\)
Оцініть кожне з наведених нижче обмежень, використовуючи «Основні результати ліміту».
- \(\displaystyle \lim_{x→2}x\)
- \(\displaystyle \lim_{x→2}5\)
Рішення
- Межа\(x\) як\(x\)\(a\) підходів\(a\):\(\displaystyle \lim_{x→2}x=2\).
- Межа константи - це те, що константа:\(\displaystyle \lim_{x→2}5=5\).
Тепер ми розглянемо граничні закони, окремі властивості лімітів. Докази, які дотримуються ці закони, тут опущені.
\(g(x)\)Дозволяти\(f(x)\) і бути визначено для всього\(x≠a\) деякого відкритого інтервалу, що містить\(a\). Припустимо, що\(L\) і\(M\) є дійсними числами такі, що\(\displaystyle \lim_{x→a}f(x)=L\) і\(\displaystyle \lim_{x→a}g(x)=M\). Нехай\(c\) буде постійною. Потім кожне з наступних тверджень тримає:
- Закон суми для лімітів:
\[\displaystyle \lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M \nonumber \]
- Закон різниці для лімітів:
\[\displaystyle \lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M \nonumber \]
- Постійний множинний закон для лімітів:
\[\displaystyle \lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber \]
- Закон про продукт для лімітів:
\[\displaystyle \lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M \nonumber \]
- Коефіцієнтний закон для лімітів:
\[\displaystyle \lim_{x→a}\frac{f(x)}{g(x)}=\frac{\displaystyle \lim_{x→a}f(x)}{\displaystyle \lim_{x→a}g(x)}=\frac{L}{M} \nonumber \]
для\(M≠0\).
- Закон влади для лімітів:
\[\displaystyle \lim_{x→a}\big(f(x)\big)^n=\big(\lim_{x→a}f(x)\big)^n=L^n \nonumber \]
за кожне натуральне число\(n\).
- Кореневий закон для лімітів:
\[\displaystyle \lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a} f(x)}=\sqrt[n]{L} \nonumber \]
для всіх\(L\) якщо\(n\) непарний і для\(L≥0\) якщо\(n\) парний.
Зараз ми практикуємо застосування цих граничних законів для оцінки ліміту.
Використовуйте граничні закони для оцінки\[\lim_{x→−3}(4x+2). \nonumber \]
Рішення
Давайте застосовуємо граничні закони один крок за кроком, щоб бути впевненими, що ми розуміємо, як вони працюють. Ми повинні мати на увазі вимогу про те, що при кожному застосуванні граничного закону повинні існувати нові межі для застосування граничного закону.
\[\begin{align*} \lim_{x→−3}(4x+2) &= \lim_{x→−3} 4x + \lim_{x→−3} 2 & & \text{Apply the sum law.}\\[4pt] &= 4⋅\lim_{x→−3} x + \lim_{x→−3} 2 & & \text{Apply the constant multiple law.}\\[4pt] &= 4⋅(−3)+2=−10. & & \text{Apply the basic limit results and simplify.} \end{align*}\]
Використовуйте граничні закони для оцінки\[\lim_{x→2}\frac{2x^2−3x+1}{x^3+4}. \nonumber \]
Рішення
Щоб знайти цю межу, нам потрібно кілька разів застосувати граничні закони. Знову ж таки, ми повинні мати на увазі, що, коли ми переписуємо ліміт з точки зору інших обмежень, кожна нова межа повинна існувати для застосування граничного закону.
\ [\ begin {align*}\ lim_ {x→2}\ розрив {2x^2−3x+1} {x^3+4} &=\ frac {\ displaystyle\ lim_ {x→2} (2x^2−3x+1)} {\ displaystyle\ lim_ {x→2} (x^3+4)}} &\ text {Застосувати частковий закон, переконайтеся, що} (2) ^3+40.\\ [4pt]
&=\ frac {\ стиль відображення 2⋅\ lim_ {x → 2} x^2−3⋅\ lim_ {x → 2} x+\ lim_ {x → 2} 1} {\ стиль відображення\ lim_ {x → 2} x^3+\ lim_ {x→2} 4} &\ text {Застосувати закон суми та постійний кратний закон.}\\ [4pt]
&=\ frac {\ displaystyle 2⋅\ left (\ lim_ {x→2} x\ праворуч) ^2−3⋅\ lim_ {x → 2} x+\ lim_ {x → 2} {x→2} (\ lim_ {x→2} x\ праворуч) ^3+\ lim_ {x→2} 4} &\ text {Застосувати закон влади.}\\ [4pt]
&=\ гідророзрив {2 (4) −3 (2) +1} {(2) ^3+4} =\ гідророзрив {1} {4}. &\ text {Застосовуйте основні закони обмеження та спростіть.} \ end {вирівнювати*}\]
Використовуйте граничні закони для оцінки\(\displaystyle \lim_{x→6}(2x−1)\sqrt{x+4}\). На кожному кроці вказуйте застосовуваний граничний закон.
- Підказка
-
Почніть із застосування закону про продукт.
- Відповідь
-
\(11\sqrt{10}\)
Додаткові методи оцінки лімітів
Як ми бачили, ми можемо легко оцінити межі поліномів і межі деяких (але не всіх) раціональних функцій шляхом прямого підстановки. Однак, як ми бачили у вступному розділі про обмеження, це, безумовно, можливо\(\displaystyle \lim_{x→a}f(x)\) існувати, коли\(f(a)\) не визначено. Наступне спостереження дозволяє оцінити багато меж цього типу:
Якщо на\(x≠a,\;f(x)=g(x)\) всьому протязі якогось відкритого інтервалу\(a\), що містить, то
\[\displaystyle\lim_{x→a}f(x)=\lim_{x→a}g(x). \nonumber \]
Щоб краще зрозуміти цю ідею, розглянемо межу\(\displaystyle \lim_{x→1}\dfrac{x^2−1}{x−1}\).
Функція
\[f(x)=\dfrac{x^2−1}{x−1}=\dfrac{(x−1)(x+1)}{x−1}\nonumber \]
і функції\(g(x)=x+1\) ідентичні для всіх значень\(x≠1\). Графіки цих двох функцій наведені на рис\(\PageIndex{1}\).
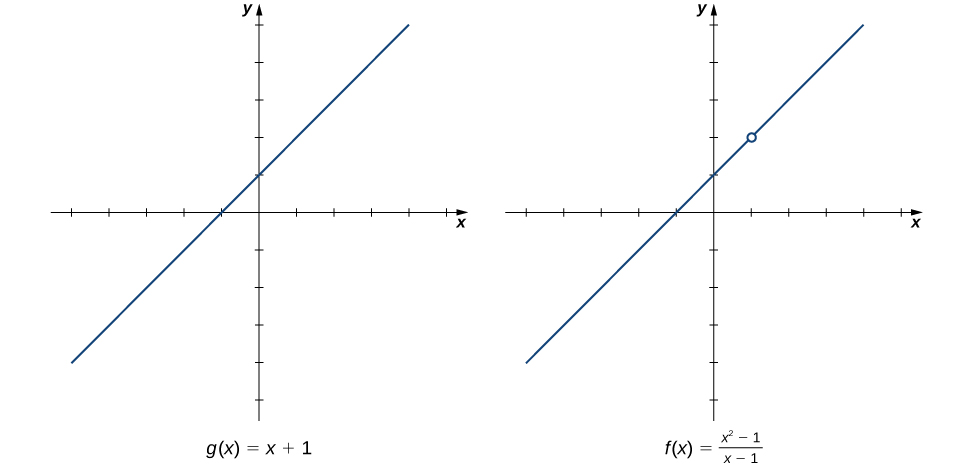
Ми бачимо, що
\[\lim_{x→1}\dfrac{x^2−1}{x−1}=\lim_{x→1}\dfrac{(x−1)(x+1)}{x−1}=\lim_{x→1}\,(x+1)=2.\nonumber \]
Ліміт має вигляд\(\displaystyle \lim_{x→a}f(x)/g(x)\), де\(\displaystyle\lim_{x→a}f(x)=0\) і\(\displaystyle\lim_{x→a}g(x)=0\). (В даному випадку ми говоримо, що\(f(x)/g(x)\) має невизначену форму\(0/0\).) Наступна стратегія вирішення проблем надає загальний план оцінки меж цього типу.
- По-перше, ми повинні переконатися, що наша функція має відповідну форму і не може бути оцінена відразу, використовуючи граничні закони.
- Потім нам потрібно знайти функцію, яка дорівнює\(h(x)=f(x)/g(x)\) для всього\(x≠a\) деякого інтервалу, що містить a. Для цього нам може знадобитися спробувати один або кілька з наступних кроків:
- Якщо\(f(x)\) і\(g(x)\) є поліномами, ми повинні враховувати кожну функцію і скасувати будь-які загальні фактори.
- Якщо чисельник або знаменник містить різницю за участю квадратного кореня, слід спробувати помножити чисельник і знаменник на сполучений виразу, що включає квадратний корінь.
- Якщо\(f(x)/g(x)\) це складний дріб, починаємо з її спрощення.
- І останнє, застосовуємо граничні закони.
Наступні приклади демонструють використання цієї Стратегії вирішення проблем. Приклад\(\PageIndex{4}\) ілюструє метод фактор-і-скасування; Приклад\(\PageIndex{5}\) показує множення на кон'югат. У\(\PageIndex{6}\) прикладі ми розглянемо спрощення складного дробу.
Оцінити\(\displaystyle\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}\).
Рішення
Крок 1. Функція\(f(x)=\dfrac{x^2−3x}{2x^2−5x−3}\) не визначена для\(x=3\). Насправді, якщо ми підставимо 3 в функцію ми отримуємо\(0/0\), яка не визначена. Факторинг і скасування - хороша стратегія:
\[\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}=\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}\nonumber \]
Крок 2. Для всіх\(x≠3,\dfrac{x^2−3x}{2x^2−5x−3}=\dfrac{x}{2x+1}\). Тому
\[\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}=\lim_{x→3}\dfrac{x}{2x+1}.\nonumber \]
Крок 3. Оцініть за допомогою граничних законів:
\[\lim_{x→3}\dfrac{x}{2x+1}=\dfrac{3}{7}.\nonumber \]
Оцінити\(\displaystyle \lim_{x→−3}\dfrac{x^2+4x+3}{x^2−9}\).
- Підказка
-
Дотримуйтесь кроків Стратегії вирішення проблем
- Відповідь
-
\(\dfrac{1}{3}\)
Оцінити\( \displaystyle \lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}\).
Рішення
Крок 1. \( \displaystyle \dfrac{\sqrt{x+2}−1}{x+1}\)має вигляд\(0/0\) −1. Почнемо з множення на\(\sqrt{x+2}+1\), сполучений з\(\sqrt{x+2}−1\), на чисельник і знаменник:
\[\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}=\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}⋅\dfrac{\sqrt{x+2}+1}{\sqrt{x+2}+1}.\nonumber \]
Крок 2. Потім множимо чисельник. Ми не множимо знаменник, тому що ми сподіваємося, що\((x+1)\) в знаменнику скасовується врешті-решт:
\[=\lim_{x→−1}\dfrac{x+1}{(x+1)(\sqrt{x+2}+1)}.\nonumber \]
Крок 3. Потім скасовуємо:
\[= \lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}.\nonumber \]
Крок 4. Нарешті, ми застосовуємо лімітні закони:
\[\lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}=\dfrac{1}{2}.\nonumber \]
Оцінити\( \displaystyle \lim_{x→5}\dfrac{\sqrt{x−1}−2}{x−5}\).
- Підказка
-
Дотримуйтесь кроків Стратегії вирішення проблем
- Відповідь
-
\(\dfrac{1}{4}\)
Оцінити\( \displaystyle \lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}\).
Рішення
Крок 1. \(\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}\)має вигляд\(0/0\) на 1. Спростимо алгебраїчний дріб множенням на\(2(x+1)/2(x+1)\):
\[\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}=\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}⋅\dfrac{2(x+1)}{2(x+1)}.\nonumber \]
Крок 2. Далі множимо через чисельники. Не множте знаменники, тому що ми хочемо мати можливість скасувати коефіцієнт\((x−1)\):
\[=\lim_{x→1}\dfrac{2−(x+1)}{2(x−1)(x+1)}.\nonumber \]
Крок 3. Потім, спрощуємо чисельник:
\[=\lim_{x→1}\dfrac{−x+1}{2(x−1)(x+1)}.\nonumber \]
Крок 4. Тепер ми обчислюємо −1 з чисельника:
\[=\lim_{x→1}\dfrac{−(x−1)}{2(x−1)(x+1)}.\nonumber \]
Крок 5. Потім скасовуємо загальні фактори\((x−1)\):
\[=\lim_{x→1}\dfrac{−1}{2(x+1)}.\nonumber \]
Крок 6. Останній, оцінюємо, використовуючи граничні закони:
\[\lim_{x→1}\dfrac{−1}{2(x+1)}=−\dfrac{1}{4}.\nonumber \]
Оцінити\( \displaystyle \lim_{x→−3}\dfrac{\dfrac{1}{x+2}+1}{x+3}\).
- Підказка
-
Дотримуйтесь кроків Стратегії вирішення проблем
- Відповідь
-
−1
Приклад\(\PageIndex{7}\) не потрапляє акуратно ні в один з шаблонів, встановлених в попередніх прикладах. Однак, маючи трохи творчості, ми все ще можемо використовувати ці самі прийоми.
Оцінити\( \displaystyle \lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)\).
Рішення:
Обидва\(1/x\)\(5/x(x−5)\) і не мають обмеження на нулі. Оскільки жодна з двох функцій не має межі на нулі, ми не можемо застосувати закон суми для лімітів; ми повинні використовувати іншу стратегію. У цьому випадку ми знаходимо межу, виконуючи додавання, а потім застосовуючи одну з наших попередніх стратегій. Зауважте, що
\[\dfrac{1}{x}+\dfrac{5}{x(x−5)}=\dfrac{x−5+5}{x(x−5)}=\dfrac{x}{x(x−5)}.\nonumber \]
Таким чином,
\[\lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)=\lim_{x→0}\dfrac{x}{x(x−5)}=\lim_{x→0}\dfrac{1}{x−5}=−\dfrac{1}{5}.\nonumber \]
Оцінити\( \displaystyle \lim_{x→3}\left(\dfrac{1}{x−3}−\dfrac{4}{x^2−2x−3}\right)\).
- Підказка
-
Використовуйте ту ж техніку, що і приклад\(\PageIndex{7}\). Не забудьте фактор,\(x^2−2x−3\) перш ніж отримати спільний знаменник.
- Відповідь
-
\(\dfrac{1}{4}\)
Давайте тепер переглянемо односторонні межі. Прості модифікації граничних законів дозволяють застосовувати їх до односторонніх меж. Наприклад, щоб застосувати граничні закони до межі форми\(\displaystyle \lim_{x→a^−}h(x)\), ми вимагаємо,\(h(x)\) щоб функція була визначена через відкритий інтервал форми\((b,a)\); для обмеження форми ми вимагаємо\(\displaystyle \lim_{x→a^+}h(x)\),\(h(x)\) щоб функція була визначена через відкритий інтервал форми\((a,c)\). Приклад\(\PageIndex{8A}\) ілюструє цей момент.
Оцініть кожен з наступних обмежень, якщо це можливо.
- \(\displaystyle \lim_{x→3^−}\sqrt{x−3}\)
- \( \displaystyle \lim_{x→3^+}\sqrt{x−3}\)
Рішення
Малюнок\(\PageIndex{2}\) ілюструє функцію\(f(x)=\sqrt{x−3}\) та допомагає в нашому розумінні цих меж.
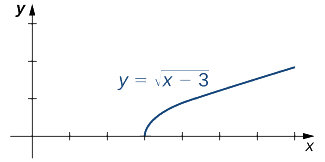
a Функція\(f(x)=\sqrt{x−3}\) визначається протягом інтервалу\([3,+∞)\). Оскільки ця функція не визначена зліва від 3, ми не можемо застосувати граничні закони для обчислення\(\displaystyle\lim_{x→3^−}\sqrt{x−3}\). Насправді, оскільки\(f(x)=\sqrt{x−3}\) не визначено зліва від 3,\(\displaystyle\lim_{x→3^−}\sqrt{x−3}\) не існує.
б Оскільки\(f(x)=\sqrt{x−3}\) визначено праворуч від 3, граничні закони застосовуються до\(\displaystyle\lim_{x→3^+}\sqrt{x−3}\). Застосовуючи ці граничні закони, ми отримуємо\(\displaystyle\lim_{x→3^+}\sqrt{x−3}=0\).
У прикладі\(\PageIndex{8B}\) ми розглянемо односторонні межі кусково визначеної функції і використовуємо ці межі, щоб зробити висновок про двосторонню межу тієї ж функції.
Для\(f(x)=\begin{cases}4x−3, & \mathrm{if} \; x<2 \\ (x−3)^2, & \mathrm{if} \; x≥2\end{cases}\), оцініть кожен з наступних меж:
- \(\displaystyle \lim_{x→2^−}f(x)\)
- \(\displaystyle \lim_{x→2^+}f(x)\)
- \(\displaystyle \lim_{x→2}f(x)\)
Рішення
Малюнок\(\PageIndex{3}\) ілюструє функцію\(f(x)\) та допомагає в нашому розумінні цих меж.
а Оскільки\(f(x)=4x−3\) для всіх\(x\) в\((−∞,2)\), замінити\(f(x)\) в ліміті на\(4x−3\) і застосовувати граничні закони:
\[\lim_{x→2^−}f(x)=\lim_{x→2^−}(4x−3)=5\nonumber \]
б. оскільки\(f(x)=(x−3)^2\) для всіх\(x\) в\((2,+∞)\), замінити\(f(x)\) в ліміті на\((x−3)^2\) і застосовувати граничні закони:
\[\lim_{x→2^+}f(x)=\lim_{x→2^−}(x−3)^2=1. \nonumber \]
c Оскільки\(\displaystyle \lim_{x→2^−}f(x)=5\) і\(\displaystyle \lim_{x→2^+}f(x)=1\), робимо висновок, що\(\displaystyle \lim_{x→2}f(x)\) не існує.
Графік\(f(x)=\begin{cases}−x−2, & \mathrm{if} \; x<−1\\ 2, & \mathrm{if} \; x=−1 \\ x^3, & \mathrm{if} \; x>−1\end{cases}\) і оцінка\(\displaystyle \lim_{x→−1^−}f(x)\).
- Підказка
-
Використовуйте метод у прикладі\(\PageIndex{8B}\) для оцінки ліміту.
- Відповідь
-
-1, яка перетинала вісь x та вісь y у початку." src="https://math.libretexts.org/@api/dek...02_03_004.jpeg">
\[\lim_{x→−1^−}f(x)=−1\nonumber \]
Тепер звернемо увагу на оцінку межі форми\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}\), де\(\displaystyle \lim_{x→a}f(x)=K\), де\(K≠0\) і\(\displaystyle \lim_{x→a}g(x)=0\). Тобто\(f(x)/g(x)\) має вигляд\(K/0,K≠0\) при\(a\).
Оцінити\(\displaystyle \lim_{x→2^−}\dfrac{x−3}{x^2−2x}\).
Рішення
Крок 1. Після підстановки в\(x=2\), ми бачимо, що цей ліміт має вигляд\(−1/0\). Тобто у міру\(x\) підходу\(2\) зліва наближається чисельник\(−1\); і наближається знаменник\(0\). Отже, величина\(\dfrac{x−3}{x(x−2)} \) стає нескінченною. Щоб отримати більш повне уявлення про те, що таке межа, нам потрібно перерахувати знаменник:
\[\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=\lim_{x→2^−}\dfrac{x−3}{x(x−2)} \nonumber \]
Крок 2. Оскільки\(x−2\) це єдина частина знаменника, яка дорівнює нулю, коли 2 підставляється, то ми відокремлюємо\(1/(x−2)\) від решти функції:
\[=\lim_{x→2^−}\dfrac{x−3}{x}⋅\dfrac{1}{x−2} \nonumber \]
Крок 3. Використовуючи граничні закони, ми можемо написати:
\[=\left(\lim_{x→2^−}\dfrac{x−3}{x}\right)\cdot\left(\lim_{x→2^−}\dfrac{1}{x−2}\right). \nonumber \]
Крок 4. \(\displaystyle \lim_{x→2^−}\dfrac{x−3}{x}=−\dfrac{1}{2}\)і\(\displaystyle \lim_{x→2^−}\dfrac{1}{x−2}=−∞\). Тому продукт\((x−3)/x\) і\(1/(x−2)\) має ліміт\(+∞\):
\[\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=+∞. \nonumber \]
Оцінити\(\displaystyle \lim_{x→1}\dfrac{x+2}{(x−1)^2}\).
- Рішення
-
Скористайтеся методами з Example\(\PageIndex{9}\).
- Відповідь
-
\(+∞\)
Теорема про стискання
Методи, які ми розробили до цього часу, дуже добре працюють для алгебраїчних функцій, але ми все ще не можемо оцінити межі дуже основних тригонометричних функцій. Наступна теорема, яка називається теоремою стискання, виявляється дуже корисною для встановлення основних тригонометричних меж. Ця теорема дозволяє обчислити межі, «стискаючи» функцію, з межею в невідомій точці між двома функціями,\(a\) що мають загальну відому межу в\(a\). Малюнок\(\PageIndex{4}\) ілюструє цю ідею.
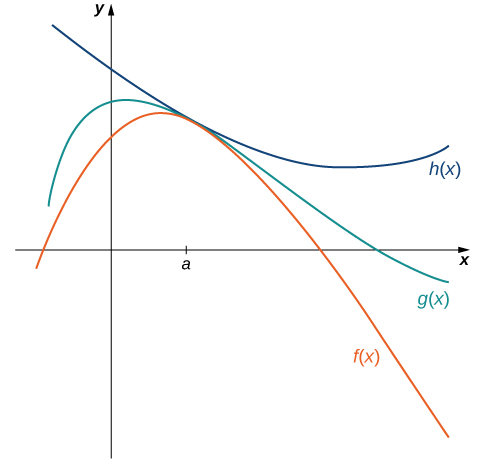
Дозволяти\(f(x),g(x)\), і\(h(x)\) бути визначені для всього\(x≠a\) відкритого інтервалу, що містить\(a\). Якщо
\[f(x)≤g(x)≤h(x) \nonumber \]
для всіх\(x≠a\) у відкритому інтервалі, що містить\(a\) і
\[\lim_{x→a}f(x)=L=\lim_{x→a}h(x) \nonumber \]
де\(L\) дійсне число, то\(\displaystyle \lim_{x→a}g(x)=L.\)
Застосуйте теорему стискання для оцінки\(\displaystyle \lim_{x→0} x \cos x\).
Рішення
Тому що\(−1≤\cos x≤1\) для всіх\(x\) ми маємо\(−x≤x \cos x≤x\) for\(x≥0\) і\(−x≥x \cos x ≥ x\) for\(x≤0\) (якщо\(x\) негативний напрямок нерівностей змінюється, коли ми множимо). Так як\(\displaystyle \lim_{x→0}(−x)=0=\lim_{x→0}x\), з теореми стискання, отримаємо\(\displaystyle \lim_{x→0}x \cos x=0\). Графіки\(f(x)=−x,\;g(x)=x\cos x\), і\(h(x)=x\) наведені на рис\(\PageIndex{5}\).
Використовуйте теорему стискання для оцінки\(\displaystyle \lim_{x→0}x^2 \sin\dfrac{1}{x}\).
- Підказка
-
Використовуйте той факт, що\(−x^2≤x^2\sin (1/x) ≤ x^2\) допоможе вам знайти дві функції такі,\(x^2\sin (1/x)\) що затиснута між ними.
- Відповідь
-
0
Тепер ми використовуємо теорему стискання для вирішення декількох дуже важливих меж. Хоча ця дискусія є дещо тривалою, ці межі виявляються неоціненними для розвитку матеріалу як у наступному розділі, так і в наступному розділі. Першим з цих меж є\(\displaystyle \lim_{θ→0}\sin θ\). Розглянемо одиничний коло, показаний на малюнку\(\PageIndex{6}\). На малюнку ми бачимо, що\(\sin θ\) це\(y\) -координата на одиничному колі, і вона відповідає відрізку лінії, показаному синім кольором. Радіан міра кута\(θ\) - це довжина дуги, яку вона підлягає на одиничному колі. Тому ми бачимо, що для\(0<θ<\dfrac{π}{2},\) нас є\(0<\sin θ<θ.\)
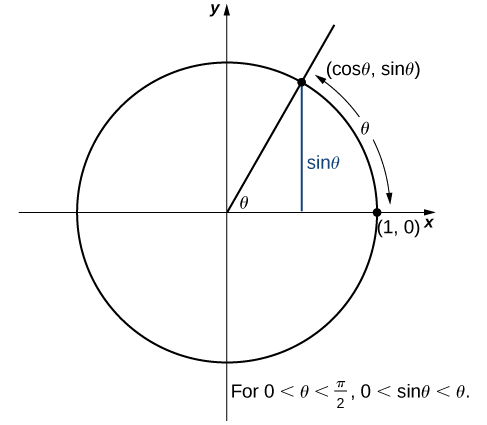
Тому що\(\displaystyle \lim_{θ→0^+}0=0\) і\(\displaystyle \lim_{x→0^+}θ=0\), використовуючи теорему стискання, ми робимо висновок, що
\[\lim_{θ→0^+}\sin θ=0.\nonumber \]
Щоб побачити це\(\displaystyle \lim_{θ→0^−}\sin θ=0\) також, спостерігайте, що для\(−\dfrac{π}{2}<θ<0,0<−θ<\dfrac{π}{2}\) і, отже,\(0<\sin(−θ)<−θ\). Отже,\(0<−\sin θ<−θ\). Звідси випливає, що\(0>\sin θ>θ\). Застосування теореми стискання виробляє бажану межу. Таким чином, так як\(\displaystyle \lim_{θ→0^+}\sin θ=0\) і\(\displaystyle \lim_{θ→0^−}\sin θ=0\),
\[\lim_{θ→0}\sin θ=0\nonumber \]
Далі, використовуючи ідентифікацію\(\cos θ=\sqrt{1−\sin^2θ}\) для\(−\dfrac{π}{2}<θ<\dfrac{π}{2}\), ми бачимо, що
\[\lim_{θ→0}\cos θ=\lim_{θ→0}\sqrt{1−\sin^2θ}=1.\nonumber \]
Зараз ми розглянемо межу, яка відіграє важливу роль у наступних розділах, а саме,\(\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}\). Щоб оцінити цю межу, скористаємося одиничним кругом на рис\(\PageIndex{7}\). Зверніть увагу, що ця цифра додає один додатковий трикутник до малюнка\(\PageIndex{6}\). Ми бачимо, що довжина сторони протилежного кута\(θ\) в цьому новому трикутнику є\(\tan θ\). Таким чином, ми бачимо, що для\(0<θ<\dfrac{π}{2}\), у нас є\(\sin θ<θ<\tanθ\).
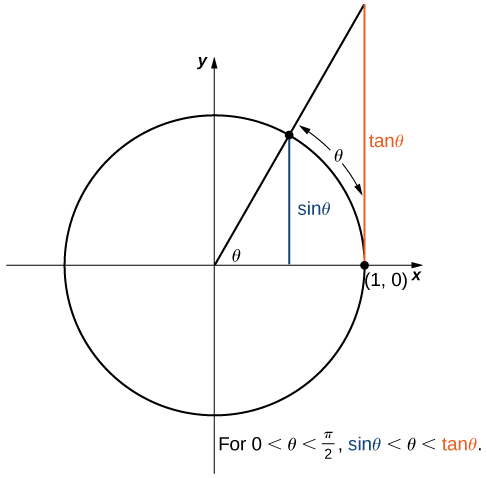
Діливши\(\sin θ\) на по всіх частинам нерівності, отримаємо
\[1<\dfrac{θ}{\sin θ}<\dfrac{1}{\cos θ}.\nonumber \]
Рівнозначно, у нас є
\[1>\dfrac{\sin θ}{θ}>\cos θ.\nonumber \]
Оскільки\(\displaystyle \lim_{θ→0^+}1=1=\lim_{θ→0^+}\cos θ\), зробимо висновок\(\displaystyle \lim_{θ→0^+}\dfrac{\sin θ}{θ}=1\), що, за теоремою стискання. Застосовуючи маніпуляцію, подібну до тієї\(\displaystyle \lim_{θ→0^−}\sin θ=0\), що використовується для демонстрації цього, ми можемо це показати\(\displaystyle \lim_{θ→0^−}\dfrac{\sin θ}{θ}=1\). Таким чином,
\[\lim_{θ→0}\dfrac{\sin θ}{θ}=1. \nonumber \]
У\(\PageIndex{11}\) прикладі ми використовуємо цей ліміт для встановлення\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0\). Ця межа також виявляється корисною в наступних розділах.
Оцінити\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}\).
Рішення
На першому кроці ми множимо на сполучений, щоб ми могли використовувати тригонометричну ідентичність для перетворення косинуса в чисельнику в синус:
\ [\ почати {вирівнювати*}\ lim_ {θ → 0}\ dfrac {1−\ cos θ} {θ} &=\ стиль відображення\ lim_ {θ → 0}\ dfrac {1−\ cos θ} {θ}\ dfrac {1+\ cos θ} {1+\ cos θ}\\ [4pt]
&=\ lim_ {θ}\ фрак {1−\ cos^2θ} {θ (1+\ cos θ)}\\ [4пт]
&=\ lim_ {θ → 0}\ dfrac {\ sin^2θ} {θ (1+\ cos θ)}\\ [4pt]
&=\ lim_ {θ → 0}\ dfrac {\ sin θ } {θ} ⋅\ dfrac {\ sin θ} {1+\ cos θ}\\ [4pt]
&=\ ліворуч (\ lim_ {θ → 0}\ dfrac {\ sin θ} {θ}\ праворуч)\ cdot\ ліворуч (\ lim_ {θ → 0}\ dfrac {\ sin θ} {1+\ cos θ}\ праворуч)\\ [4pt]
&= 1⋅\ фрак {0} {2} =0. \ end {вирівнювати*}\]
Тому
\[\lim_{θ→0}\dfrac{1−\cos θ}{θ}=0. \nonumber \]
Оцінити\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{\sin θ}\).
- Підказка
-
Помножте чисельник і знаменник на\(1+\cos θ\).
- Відповідь
-
0
Деякі геометричні формули, які ми сьогодні сприймаємо як належне, були вперше отримані методами, які передбачають деякі методи обчислення. Грецький математик Архімед (бл. 287−212; до н.е.) був особливо винахідливим, використовуючи багатокутники, вписані в кола, для наближення площі кола у міру збільшення кількості сторін багатокутника. Він ніколи не придумав ідеї обмеження, але ми можемо використовувати цю ідею, щоб побачити, що його геометричні конструкції могли передбачити про межу.
Ми можемо оцінити площу кола, обчисливши площу вписаного правильного багатокутника. Подумайте про правильний багатокутник як про те, що складається з\(n\) трикутників. Прийнявши межу, оскільки кут вершини цих трикутників йде до нуля, можна отримати площу кола. Щоб переконатися в цьому, виконайте наступні дії:
1.Висловіть висоту\(h\) і\(b\) підставу рівнобедреного трикутника на малюнку\(\PageIndex{8}\) в терміні\(θ\) і\(r\).
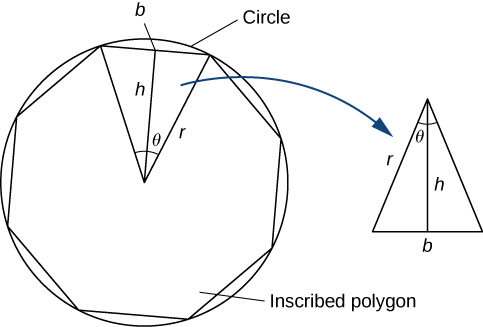
2. Використовуючи вирази, які ви отримали на кроці 1, висловіть площу рівнобедреного трикутника через\(θ\) і\(r\).
(\(\frac{1}{2}\sin θ\)Замініть\(\sin\left(\frac{θ}{2}\right)\cos\left(\frac{θ}{2}\right)\) у вашому вираженні.)
3. Якщо\(n\) -односторонній правильний багатокутник вписаний в коло радіуса\(r\), знайдіть співвідношення між\(θ\) і\(n\). Вирішити це для\(n\). Майте на увазі, що в колі є\(2π\) радіани. (Використовуйте радіани, а не градуси.)
4. Знайти вираз для площі\(n\) -одностороннього багатокутника через\(r\) і\(θ\).
5. Щоб знайти формулу для площі кола, знайдіть межу виразу в кроці 4, як\(θ\) йде до нуля. (Підказка:\(\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}=1)\).
Методику оцінки площ регіонів за допомогою полігонів переглянуто у Вступі до інтеграції.
Ключові поняття
- Граничні закони дозволяють оцінювати межі функцій без необхідності кожного разу проходити покрокові процеси.
- Для поліномів і раціональних функцій,\[\lim_{x→a}f(x)=f(a). \nonumber \]
- Оцінити межу функції можна шляхом факторингу та скасування, множення на сполучений, або спрощення складного дробу.
- Теорема стискання дозволяє знайти межу функції, якщо функція завжди більша за одну функцію і менше іншої функції з відомими межами.
Ключові рівняння
- Основні лімітні результати
\[\lim_{x→a}x=a \quad \quad \lim_{x→a}c=c \nonumber \]
- Важливі межі
\[ \lim_{θ→0}\sin θ=0 \nonumber \]
\[ \lim_{θ→0}\cos θ=1 \nonumber \]
\[ \lim_{θ→0}\dfrac{\sin θ}{θ}=1 \nonumber \]
\[ \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0 \nonumber \]
Глосарій
- постійний множинний закон для обмежень
- граничний закон\[\lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber \]
- закон різниці для лімітів
- граничний закон\[\lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M\nonumber \]
- граничні закони
- індивідуальні властивості меж; для кожного з окремих законів, нехай\(f(x)\) і\(g(x)\) бути визначені для всього\(x≠a\) деякого відкритого інтервалу, що містить a; припустимо, що L і M є дійсними числами, так що\(\lim_{x→a}f(x)=L\) і\(\lim_{x→a}g(x)=M\); нехай c бути постійною
- закон влади для лімітів
- граничний закон\[\lim_{x→a}(f(x))^n=(\lim_{x→a}f(x))^n=L^n\nonumber \] для кожного натурального числа n
- закон про продукт для лімітів
- граничний закон\[\lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M\nonumber \]
- часткове право для лімітів
- граничний закон\(\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{\lim_{x→a}f(x)}{\lim_{x→a}g(x)}=\dfrac{L}{M}\) для M0
- кореневий закон для лімітів
- граничний закон\(\lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a}f(x)}=\sqrt[n]{L}\) для всіх L, якщо n непарний, а для\(L≥0\) якщо n парний
- теорема стискання
- стверджує, що якщо\(f(x)≤g(x)≤h(x)\) для\(x≠a\) всього відкритого інтервалу, що містить a і\(\lim_{x→a}f(x)=L=\lim_ {x→a}h(x)\) де L - дійсне число, то\(\lim_{x→a}g(x)=L\)
- закон суми для лімітів
- Граничний закон\(\lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M\)

Межі поліноміальних і раціональних функцій
На даний момент ви, напевно, помітили, що в кожному з попередніх прикладів це було так\(\displaystyle \lim_{x→a}f(x)=f(a)\). Це не завжди вірно, але воно стосується всіх поліномів для будь-якого вибору\(a\) та для всіх раціональних функцій при всіх значеннях,\(a\) для яких визначена раціональна функція.
Межі поліноміальних і раціональних функцій
\(q(x)\)Дозволяти\(p(x)\) і бути поліноміальними функціями. \(a\)Дозволяти бути дійсним числом. Потім,
\[\lim_{x→a}p(x)=p(a) \nonumber \]
\[\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)} \nonumber \]
коли\(q(a)≠0\).
Щоб побачити, що ця теорема тримає, розглянемо многочлен
\[p(x)=c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0. \nonumber \]
Застосовуючи закони суми, постійні кратні та владні закони, ми закінчуємо
\[ \begin{align*} \lim_{x→a}p(x) &= \lim_{x→a}(c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0) \\[4pt] &= c_n\left(\lim_{x→a}x\right)^n+c_{n−1}\left(\lim_{x→a}x\right)^{n−1}+⋯+c_1\left(\lim_{x→a}x\right)+\lim_{x→a}c_0 \\[4pt] &= c_na^n+c_{n−1}a^{n−1}+⋯+c_1a+c_0 \\[4pt] &= p(a) \end{align*}\]
Тепер з часткового закону випливає, що якщо\(p(x)\) і\(q(x)\) є поліномами, для яких\(q(a)≠0\),
потім
\[\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}. \nonumber \]
Приклад\(\PageIndex{3}\): Evaluating a Limit of a Rational Function
Оцініть\(\displaystyle \lim_{x→3}\frac{2x^2−3x+1}{5x+4}\).
Рішення
Оскільки 3 знаходиться в області раціональної функції\(f(x)=\displaystyle \frac{2x^2−3x+1}{5x+4}\), ми можемо обчислити межу, підставивши 3 for\(x\) у функцію. Таким чином,
\[\lim_{x→3}\frac{2x^2−3x+1}{5x+4}=\frac{10}{19}. \nonumber \]
Вправа\(\PageIndex{3}\)
Оцінити\(\displaystyle \lim_{x→−2}(3x^3−2x+7)\).
Використання меж поліноміальних та раціональних функцій як посилання
−13