2.4: Безперервність

Last updated
Save as PDF

Page ID: 62351

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Поясніть три умови безперервності в точці.
Опишіть три види розривів.
Визначте безперервність на інтервалі.
Створіть теорему для меж композиційних функцій.
Наведіть приклад теореми про проміжні значення.

Багато функцій мають властивість, що їх графіки можна простежити олівцем, не відриваючи олівець зі сторінки. Такі функції називаються безперервними. Інші функції мають точки, в яких відбувається розрив графіка, але задовольняють цю властивість протягом інтервалів, що містяться в їх областях. Вони безперервні на цих інтервалах і, як кажуть, мають розрив у точці, де відбувається розрив.

Ми починаємо наше дослідження безперервності з вивчення того, що означає функція мати безперервність у точці. Інтуїтивно функція є безперервною в певній точці, якщо немає розриву в її графіку в цій точці.

Безперервність у точці

Перш ніж ми розглянемо формальне визначення того, що це означає для функції, щоб бути безперервною в точці, давайте розглянемо різні функції, які не відповідають нашому інтуїтивному уявленню про те, що означає бути безперервним в точці. Потім ми створюємо список умов, які запобігають подібним збоям.

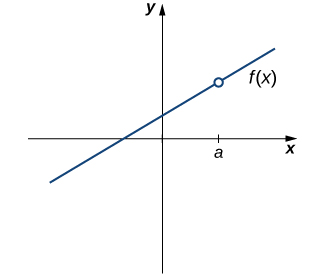
Наша перша цікава функція показана на малюнку\(\PageIndex{1}\). Ми бачимо, що графік\(f(x)\) має дірку в\(a\). Насправді,\(f(a)\) не визначено. По крайней мере, для\(f(x)\) того, щоб бути безперервним в\(a\), нам потрібна наступна умова:

i.\(f(a)\) Визначено

Графік зростаючої лінійної функції f (x), яка перетинає вісь x від третього квадранта до другого квадранта та який перетинає вісь y від квадранта два до квадранта. На осі x відзначена точка більша за нуль. Точка на функції f (x) над a - це відкрите коло; функція не визначена при a. — Рисунок\(\PageIndex{1}\): Функція не\(f(x)\) є\(f(a)\) безперервною,\(a\) оскільки не визначена.

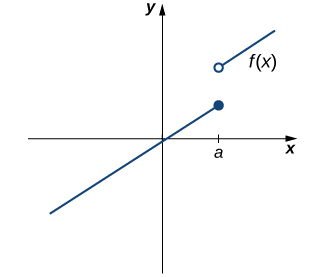
Однак, як ми бачимо на малюнку\(\PageIndex{2}\), лише ця умова недостатня, щоб гарантувати безперервність у точці\(a\). Хоча\(f(a)\) визначено, функція має розрив при\(a\). У цьому прикладі розрив існує, оскільки\(\displaystyle \lim_{x→a}f(x)\) не існує. Ми повинні додати ще одну умову для безперервності в\(a\) —а саме:

II. \(\displaystyle \lim_{x→a}f(x)\)існує

Графік кускової функції f (x) з двома частинами. Перша частина - це зростаюча лінійна функція, яка перетинає від третього квадранта до одного квадранта біля початку. На осі x відзначена точка більша за нуль. При fa. на цьому відрізку є суцільне коло. Інший сегмент також є зростаючою лінійною функцією. Він існує в одному квадранті для значень x більше, ніж a. У x = a цей відрізок має відкрите коло. — Малюнок\(\PageIndex{2}\): Функція не\(f(x)\) є безперервною,\(a\) оскільки\(\displaystyle \lim_{x→a}f(x)\) не існує.

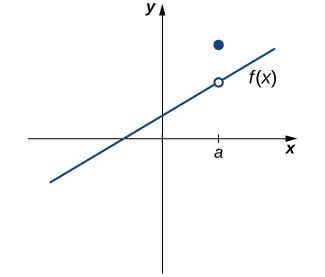
Однак, як ми бачимо на малюнку\(\PageIndex{3}\), ці дві умови самі по собі не гарантують безперервності в точці. Функція на цьому малюнку задовольняє обом нашим першим двом умовам, але все ще не є безперервною при\(a\). Ми повинні додати третю умову до нашого списку:

ііі. \(\displaystyle \lim_{x→a}f(x)=f(a)\)

Графік кускової функції з двома частинами. Перша частина - це зростаюча лінійна функція, яка перетинає вісь x від третього квадранта до квадранта два і яка перетинає вісь y від квадранта два до квадранта. На осі x відзначена точка більша за нуль. У цей момент на лінійній функції є розімкнуте коло. Друга частина - це точка на x = a над лінією. — Малюнок\(\PageIndex{3}\): Функція не\(f(x)\) є безперервною\(a\), оскільки\(\displaystyle \lim_{x→a}f(x)≠f(a)\).

Тепер ми складаємо наш список умов разом і формуємо визначення безперервності в точці.

Визначення: Безперервна в точці

Функція\(f(x)\) є неперервною в точці \(a\)тоді і лише тоді, коли виконуються наступні три умови:

\(f(a)\)визначено
\(\displaystyle \lim_{x→a}f(x)\)існує
\(\displaystyle \lim_{x→a}f(x)=f(a)\)

Функція переривається в точці,\(a\) якщо вона не може бути безперервною в\(a\).

Наступна процедура може бути використана для аналізу неперервності функції в точці, використовуючи це визначення.

Стратегія вирішення проблем: визначення безперервності в точці

Перевірте, чи\(f(a)\) визначено. Якщо\(f(a)\) не визначено, нам не потрібно йти далі. Функція не є безперервною,\(a.\) якщо\(f(a)\) визначено, перейдіть до кроку 2.
Обчислити\(\displaystyle \lim_{x→a}f(x)\). У деяких випадках нам може знадобитися зробити це за допомогою перших обчислень\(\displaystyle \lim_{x→a^−}f(x)\) і\(\displaystyle \lim_{x→a^+}f(x)\). Якщо\(\displaystyle \lim_{x→a}f(x)\) не існує (тобто це не дійсне число), значить функція не є безперервною at\(a\) і проблема вирішена. Якщо\(\displaystyle \lim_{x→a}f(x)\) існує, то перейдіть до кроку 3.
Порівняйте\(f(a)\) і\(\displaystyle \lim_{x→a}f(x)\). Якщо\(\displaystyle \lim_{x→a}f(x)≠f(a)\), то функція не є безперервною в\(a.\) If\(\displaystyle \lim_{x→a}f(x)=f(a)\), то функція безперервна при\(a.\)

Наступні три приклади демонструють, як застосувати це визначення, щоб визначити, чи є функція безперервною в заданій точці. Ці приклади ілюструють ситуації, в яких кожна з умов безперервності у визначенні досягає успіху або невдачі.

Приклад\(\PageIndex{1A}\): Determining Continuity at a Point, Condition 1

Використовуючи визначення, визначте, чи\(f(x)=\dfrac{x^2−4}{x−2}\) є функція безперервною в\(x=2\). Обгрунтуйте висновок.

Рішення

Почнемо з того, що спробуємо обчислити\(f(2)\). Ми бачимо\(f(2)=0/0\), що, що не визначено. Тому\(f(x)=\dfrac{x^2−4}{x−2}\) є переривчастим в\(2\) тому\(f(2)\), що не визначено. Графік\(f(x)\) показаний на рис\(\PageIndex{4}\).

Графік заданої функції. Існує лінія, яка перетинає вісь x від квадранта три до квадранта два і яка перетинає вісь y від квадранта два до квадранта. У точці в квадранті є відкрите коло, де функція не визначена. — Малюнок\(\PageIndex{4}\): Функція\(f(x)\) є переривчастою в\(2\)\(f(2)\) тому, що не визначена.

Приклад\(\PageIndex{1B}\): Determining Continuity at a Point, Condition 2

Використовуючи визначення, визначте, чи\(f(x)=\begin{cases}−x^2+4, & \mathrm{if} \; x≤3 \\ 4x−8, & \mathrm{if} \; x>3\end{cases}\) є функція безперервною в\(x=3\). Обгрунтуйте висновок.

Рішення

Почнемо з того, що спробуємо обчислити\(f(3)\).

\(f(3)=−(3^2)+4=−5\).

Таким чином,\(f(3)\) визначається. Далі проводимо розрахунок\(\displaystyle \lim_{x→3}f(x)\). Для цього ми повинні обчислити\(\displaystyle \lim_{x→3^−}f(x)\) і\( \displaystyle \lim_{x→3^+}f(x)\):

\(\displaystyle \lim_{x→3^−}f(x)=−(3^2)+4=−5\)

\(\displaystyle \lim_{x→3^+}f(x)=4(3)−8=4\).

Тому\(\displaystyle \lim_{x→3}f(x)\) не існує. Таким чином, не\(f(x)\) є безперервним при 3. Графік\(f(x)\) показаний на рис\(\PageIndex{5}\).

Графік заданої кускової функції, яка має дві частини. Перший - це парабола, що відкривається вниз, яка симетрична щодо осі y. Його вершина знаходиться на осі y, більша за нуль. На параболі є замкнуте коло для x=3. Друга частина - це зростаюча лінійна функція в першому квадранті, яка існує для значень x — Малюнок\(\PageIndex{5}\): Функція не\(f(x)\) є безперервною на 3, оскільки\(\displaystyle \lim_{x→3}f(x)\) не існує.

Приклад\(\PageIndex{1C}\): Determining Continuity at a Point, Condition 3

Використовуючи визначення, визначте, чи\(f(x)=\begin{cases}\frac{\sin x}{x}, & \text{if } x≠0\\1, & \text{if } x=0\end{cases}\) є функція безперервною в\(x=0\).

Рішення

По-перше, зауважте, що

\(f(0)=1\)

Наступний,

\(\displaystyle \lim_{x→0}f(x)=\lim_{x→0}\frac{\sin x}{x}=1\).

Останній,\(f(0)\) порівняємо і\(\displaystyle \lim_{x→0}f(x)\). Ми бачимо, що

\(\displaystyle f(0)=1=\lim_{x→0}f(x)\).

Так як всі три умови при визначенні безперервності задовольняються,\(f(x)\) є безперервним при\(x=0\).

Вправа\(\PageIndex{1}\)

Використовуючи визначення, визначте, чи\(f(x)=\begin{cases}2x+1, & \text{if }x<1\\2, & \text{if }x=1\\ −x+4, & \text{if }x>1\end{cases}\) є функція безперервною в\(x=1\). Якщо функція не є безперервною в 1, вкажіть умову безперервності в точці, яка не вдається утримувати.

Підказка: Перевірте кожну умову визначення.

Відповідь: \(f\)не є безперервним,\(1\) тому що\(\displaystyle f(1)=2≠3=\lim_{x→1}f(x)\).

Застосовуючи визначення неперервності і раніше встановлені теореми, що стосуються оцінки меж, можна констатувати наступну теорему.

Теорема\(\PageIndex{1}\): Continuity of Polynomials and Rational Functions

Поліноми та раціональні функції є неперервними в кожній точці своїх областей.

Доказ

Раніше ми показали, що якщо\(p(x)\) і\(q(x)\) є поліномами,\(\displaystyle \lim_{x→a}p(x)=p(a)\) для кожного многочлена\(p(x)\) і до тих\(\displaystyle \lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}\) пір, поки\(q(a)≠0\). Тому поліноми і раціональні функції є неперервними за своїми областями.

□

Тепер ми застосуємо теорему\(\PageIndex{1}\) для визначення точок, в яких задана раціональна функція є безперервною.

Приклад\(\PageIndex{2}\):Continuity of a Rational Function

Для яких значень х є\(f(x)=\dfrac{x+1}{x−5}\) безперервним?

Рішення

Раціональна функція\(f(x)=\dfrac{x+1}{x−5}\) є безперервною для кожного значення\(x\) except\(x=5\).

Вправа\(\PageIndex{2}\)

Для яких значень\(x\) є\(f(x)=3x^4−4x^2\) безперервним?

Підказка: Використовуйте неперервність поліномів і раціональних функцій, зазначених вище.

Відповідь: \(f(x)\)є безперервним при кожному дійсному числі.

види розривів

Як ми бачили в\(\PageIndex{1A}\) прикладі та прикладі\(\PageIndex{1B}\), розриви набувають кілька різних виступів. Ми класифікуємо типи розривів, які ми бачили до цього часу, як знімні розриви, нескінченні розриви або розриви стрибків. Інтуїтивно знімний розрив - це розрив, для якого в графіку є дірка, стрибок розриву - це ненескінченний розрив, для якого ділянки функції не зустрічаються, а нескінченний розрив - це розрив, розташований на вертикальна асимптота. Малюнок\(\PageIndex{6}\) ілюструє відмінності в цих типах розривів. Хоча ці терміни забезпечують зручний спосіб опису трьох поширених типів розривів, майте на увазі, що не всі розриви чітко вписуються в ці категорії.

Три графіки, кожен з яких показує різний розрив. Перший - це знімний розрив. Тут задана функція є лінією з позитивним нахилом. У точці x = a, де a — Малюнок\(\PageIndex{6}\): Розриви класифікуються як (а) знімний, (б) стрибок або (в) нескінченний.

Ці три розриви формально визначаються наступним чином:

Визначення

Якщо\(f(x)\) переривчастий в\(a,\) то

1. \(f\)має знімний розрив\(a\) при\(\displaystyle \lim_{x→a}f(x)\) наявності. (Примітка: Коли ми стверджуємо, що\(\displaystyle \lim_{x→a}f(x)\) існує, ми маємо на увазі\(\displaystyle \lim_{x→a}f(x)=L\), що, де\(L\) є дійсне число.)

2. \(f\)має стрибок розриву при\(a\) якщо\(\displaystyle \lim_{x→a^−}f(x)\) і\(\displaystyle \lim_{x→a^+}f(x)\) обидва існують, але\(\displaystyle \lim_{x→a^−}f(x)≠lim_{x→a^+}f(x)\). (Примітка: Коли ми заявляємо, що\(\displaystyle \lim_{x→a^−}f(x)\) і\(\displaystyle \lim_{x→a^+}f(x)\) обидва існують, ми маємо на увазі, що обидва є реальними і що ні приймають значення\(±∞\).)

3. \(f\)має нескінченний розрив при\(a\) if\(\displaystyle \lim_{x→a^−}f(x)=±∞\) або\(\displaystyle \lim_{x→a^+}f(x)=±∞\).

Приклад\(\PageIndex{3}\): Classifying a Discontinuity

У прикладі\(\PageIndex{1A},\) ми показали, що\(f(x)=\dfrac{x^2−4}{x−2}\) є переривчастим в\(x=2\). Класифікуйте цей розрив як знімний, стрибок або нескінченний.

Рішення

Для класифікації розриву на\(2\) ми повинні оцінити\(\displaystyle \lim_{x→2}f(x)\):

\ (\ стиль відображення\ почати {вирівнювати*}\ lim_ {x → 2} f (x) &=\ lim_ {x→2}\ розрив {x^2−4} {x−2}\ [4pt]
&=\ lim_ {x → 2}\ frac {(x−2) (x+2)} {x−2}\\ [4pt]
&=\ lim_ {x→2} (x+2)\\ [4пт]
&=4. \ end {вирівнювати*}\)

Так як\(f\) є переривчастим при\(2\) і\(\displaystyle \lim_{x→2}f(x)\) існує,\(f\) має знімний розрив при\(x=2\).

Приклад\(\PageIndex{4}\): Classifying a Discontinuity

У прикладі ми показали\(\PageIndex{1B}\), що\(f(x)=\begin{cases}−x^2+4, &\text{if }x≤3\\4x−8, &\text{if }x>3\end{cases}\) є переривчастим в\(x=3\). Класифікуйте цей розрив як знімний, стрибок або нескінченний.

Рішення

Раніше ми показали, що\(f\) є переривчастим в\(3\) тому, що\(\displaystyle \lim_{x→3}f(x)\) не існує. Однак, оскільки\(\displaystyle \lim_{x→3^−}f(x)=−5\) і те, і\(\displaystyle \lim_{x→3^+}f(x)=4\) інше існують, ми робимо висновок, що функція має стрибок розриву при\(3\).

Приклад\(\PageIndex{5}\): Classifying a Discontinuity

Визначте\(f(x)=\dfrac{x+2}{x+1}\), чи є безперервним при\(−1\). Якщо функція переривається в\(−1\), класифікуйте розрив як знімний, стрибок або нескінченний.

Рішення

Значення функції\(f(−1)\) undefined. Тому функція не є безперервною при\(−1\). Щоб визначити тип розриву, треба визначити межу при\(−1\). Ми бачимо, що\(\displaystyle \lim_{x→−1^−}\frac{x+2}{x+1}=−∞\) і\(\displaystyle \lim_{x→−1^+}\frac{x+2}{x+1}=+∞\). Тому функція має нескінченний розрив при\(−1\).

Вправа\(\PageIndex{3}\)

Для\(f(x)=\begin{cases}x^2, &\text{if }x≠1\\3, & \text{if }x=1\end{cases}\), вирішити, чи\(f\) є безперервним на\(1\). Якщо не\(f\) є безперервним при\(1\), класифікуйте розрив як знімний, стрибок або нескінченний.

Підказка: Розглянемо описані вище визначення різного роду розривів. Якщо функція переривається\(1\), подивіться на\(\displaystyle \lim_{x→1}f(x)\)

Відповідь: Переривчастий ат\(1\); знімний

Безперервність протягом інтервалу

Тепер, коли ми вивчили концепцію безперервності в точці, ми поширюємо цю ідею на безперервність протягом певного інтервалу. Коли ми розвиваємо цю ідею для різних типів інтервалів, може бути корисно мати на увазі інтуїтивну ідею про те, що функція є безперервною протягом інтервалу, якщо ми можемо використовувати олівець, щоб простежити функцію між будь-якими двома точками інтервалу, не піднімаючи олівець з паперу. Готуючись до визначення безперервності на інтервалі, ми починаємо з визначення того, що означає функція бути безперервною справа в точці і безперервною зліва в точці.

Визначення: Безперервність справа і зліва

\(f(x)\)Функція, як кажуть, безперервна справа,\(a\) якщо\(\displaystyle \lim_{x→a^+}f(x)=f(a)\).

\(f(x)\)Функція, як кажуть, безперервна зліва,\(a\) якщо\(\displaystyle \lim_{x→a^−}f(x)=f(a)\)

Функція є безперервною протягом відкритого інтервалу, якщо вона безперервна в кожній точці інтервалу. Функція\(f(x)\) є безперервною протягом замкнутого інтервалу форми,\([a,b]\) якщо вона безперервна в кожній точці в\((a,b)\)\(a\) і безперервна справа в і безперервна зліва в\(b.\) Аналогічно, функція\(f(x)\) безперервна протягом інтервалу форми \((a,b]\)якщо він безперервний над\((a,b)\) і безперервний зліва при\(b.\) Безперервність над іншими типами інтервалів визначаються аналогічним чином.

Вимагаючи цього\(\displaystyle \lim_{x→a^+}f(x)=f(a)\) і\(\displaystyle \lim_{x→b^−}f(x)=f(b)\) гарантує, що ми можемо простежити графік функції від точки\((a,f(a))\) до точки,\((b,f(b))\) не піднімаючи олівець. Якщо, наприклад\(\displaystyle \lim_{x→a^+}f(x)≠f(a)\), нам потрібно буде підняти наш олівець, щоб перейти від\(f(a)\) до графіка решти функції над\((a,b]\).

Приклад\(\PageIndex{6}\): Continuity on an Interval

Вкажіть інтервал (и), протягом якого функція\(f(x)=\dfrac{x−1}{x^2+2x}\) є безперервною.

Рішення

Оскільки\(f(x)=\dfrac{x−1}{x^2+2x}\) є раціональною функцією, вона є безперервною в кожній точці своєї області. Домен\(f(x)\) - це набір\((−∞,−2)∪(−2,0)∪(0,+∞)\). Таким чином,\(f(x)\) відбувається безперервний над кожним з інтервалів\((−∞,−2),(−2,0)\), і\((0,+∞)\).

Приклад\(\PageIndex{7}\): Continuity over an Interval

Вкажіть інтервал (и), протягом якого функція\(f(x)=\sqrt{4−x^2}\) є безперервною.

Рішення

З граничних законів ми знаємо, що\(\displaystyle \lim_{x→a}\sqrt{4−x^2}=\sqrt{4−a^2}\) для всіх значень a in\((−2,2)\). Ми також знаємо, що\(\displaystyle \lim_{x→−2^+}\sqrt{4−x^2}=0\) існує і\(\displaystyle \lim_{x→2^−}\sqrt{4−x^2}=0\) існує. Тому\(f(x)\) відбувається безперервно протягом інтервалу\([−2,2]\).

Вправа\(\PageIndex{4}\)

Вкажіть інтервал (и), протягом якого функція\(f(x)=\sqrt{x+3}\) є безперервною.

Підказка: Використовуйте\(\PageIndex{7}\) Example як орієнтир.

Відповідь: \([−3,+∞)\)

Теорема\(\PageIndex{2}\) дозволяє розширити нашу здатність обчислювати межі. Зокрема, ця теорема в кінцевому підсумку дозволяє продемонструвати, що тригонометричні функції є неперервними над своїми областями.

Теорема\(\PageIndex{2}\): Composite Function Theorem

Якщо\(f(x)\) безперервний при\(L\) і\(\displaystyle \lim_{x→a}g(x)=L\), то

\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L).\)

Перш ніж перейти до Прикладу\(\PageIndex{8},\) нагадаємо, що раніше, в розділі про граничні закони, ми показали\(\displaystyle \lim_{x→0}\cos x=1=\cos(0)\). Отже, ми знаємо, що\(f(x)=\cos x\) є безперервним в\(0\). У прикладі\(\PageIndex{8},\) ми бачимо, як поєднати цей результат з теоремою складеної функції.

Приклад\(\PageIndex{8}\): Limit of a Composite Cosine Function

Оцінити\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)\).

Рішення

Дана функція є складовою\(\cos x\) і\(x−\frac{π}{2}\). Оскільки\(\displaystyle \lim_{x→π/2}\left(x−\frac{π}{2}\right)=0\) і\(\cos x\) є неперервним at\(0\), ми можемо застосувати теорему про складену функцію. Таким чином,

\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)=\cos\left(\lim_{x→π/2}\left(x−\frac{π}{2}\right)\right)=\cos(0)=1.\)

Вправа\(\PageIndex{4}\):

Оцінити\(\displaystyle \lim_{x→π}\sin(x−π)\).

Підказка: \(f(x)=\sin x\)є безперервним при\(0\). Використовуйте\(\PageIndex{8}\) Example як орієнтир.

Відповідь: \(0\)

Доказ наступної теореми використовує теорему композитних функцій, а також неперервність\(f(x)=\sin x\) і\(g(x)=\cos x\) в точці,\(0\) щоб показати, що тригонометричні функції є неперервними по всій їх області.

Теорема\(\PageIndex{3}\): Continuity of Trigonometric Functions

Тригонометричні функції є безперервними по всій їх області.

Доказ

Ми починаємо з демонстрації, що\(\cos x\) є безперервним у кожному дійсному числі. Для цього треба показати, що\(\displaystyle \lim_{x→a}\cos x=\cos a\) для всіх значень\(a\).

\ (\ стиль відображення\ почати {вирівнювати*}\ lim_ {x→a}\ cos x &=\ lim_ {x→a}\ cos ((x−a) +a) &\ текст {Переписати} x = x−a+a.\\ [4pt]
&=\ lim_ {x → a} (\ cos (x−a)\ cos a−\ sin (x−a)\ sin a) &\ text {Застосувати ідентичність для косинуса суми двох кутів.}\\ [4pt]
&=\ cos (\ lim_ {x→a} (x−a) ))\ cos a−\ sin (\ lim_ {x→a} (x−a))\ sin a &\ text {Оскільки}\ lim_ {x→a} (x−a) =0,\ text {і}\ sin x\ text {і}\ cos x\ text {безперервні в} 0.\\ [4pt]
&=\ cos (0)\ cos a−\ sin (0)\ sin a &\ text {Оцінити}\ cos (0)\ текст {і}\ sin (0)\ текст {і спростити.}\\ [4pt]
&= 1⋅\ cos a −0⋅\ sin a=\ cos a.\ end {align*}\)

Доказ, який\(\sin x\) є безперервним у кожному дійсному числі, є аналогічним. Оскільки інші тригонометричні функції можуть бути виражені через\(\sin x\) і\(\cos x\), їх неперервність випливає з часткового граничного закону.

□

Як бачите, теорема складеної функції є неоціненною для демонстрації неперервності тригонометричних функцій. Продовжуючи вивчення числення, ми переглядаємо цю теорему багато разів.

Теорема про проміжні значення

Функції, які є безперервними над інтервалами форми\([a,b]\), де\(a\) і\(b\) є дійсними числами, проявляють безліч корисних властивостей. Протягом нашого вивчення числення ми зіткнемося з багатьма потужними теоремами, що стосуються таких функцій. Перша з цих теорем - теорема про проміжні значення.

Теорема про проміжні значення

\(f\)Дозволяти бути безперервним протягом замкнутого, обмеженого інтервалу\([a,b]\). Якщо\(z\) будь-яке дійсне число між\(f(a)\) і\(f(b)\), то є число\(c\)\(f(c)=z\) в\([a,b]\) задоволенні на малюнку\(\PageIndex{7}\).

Діаграма, що ілюструє теорему про проміжні значення. Існує загальна безперервна вигнута функція, показана протягом інтервалу [a, b]. Точки fa. і fb. позначаються, а пунктирними лініями проводять від a, b, fa., і fb. до точок (a, фа.) і (b, fb.). Третя точка, c, наноситься між a і b. Оскільки функція є безперервною, існує значення fc. уздовж кривої, а лінія проводиться від c до (c, fc.) і від (c, fc.) до fc., яка позначена як z на осі y. — Малюнок\(\PageIndex{7}\): Існує число\(c ∈ [a,b]\), яке задовольняє\(f(c)=z\).

Приклад\(\PageIndex{9}\): Application of the Intermediate Value Theorem

Показати, що\(f(x)=x−\cos x\) має принаймні один нуль.

Рішення

Оскільки\(f(x)=x−\cos x\) безперервний над\((−∞,+∞)\), він безперервний протягом будь-якого замкнутого інтервалу форми\([a,b]\). Якщо ви можете знайти інтервал\([a,b]\) такий, що\(f(a)\) і\(f(b)\) мають протилежні ознаки, ви можете використовувати теорему про проміжні значення, щоб зробити висновок, що має бути дійсне число\(c\)\((a,b)\), яке задовольняє\(f(c)=0\). Зауважте, що

\(f(0)=0−\cos(0)=−1<0\)

\(f(\frac{π}{2})=\frac{π}{2}−\cos\frac{π}{2}=\frac{π}{2}>0\).

Використовуючи теорему про проміжні значення, ми можемо побачити, що має бути дійсне число\(c\)\([0,π/2]\), яке задовольняє\(f(c)=0\). Тому\(f(x)=x−\cos x\) має хоча б один нуль.

Приклад\(\PageIndex{10}\): When Can You Apply the Intermediate Value Theorem?

Якщо\(f(x)\) безперервно закінчено\([0,2],f(0)>0\) і\(f(2)>0\), чи можемо ми використовувати теорему проміжних значень, щоб зробити висновок,\(f(x)\) що в інтервалі немає нулів\([0,2]\)? Поясніть.

Рішення

Ні. Теорема про проміжні значення дозволяє лише зробити висновок, що ми можемо знайти значення між\(f(0)\) і\(f(2)\); це не дозволяє нам зробити висновок, що ми не можемо знайти інші значення. Щоб побачити це більш наочно, розглянемо функцію\(f(x)=(x−1)^2\). Це задовольняє\(f(0)=1>0,f(2)=1>0\), і\(f(1)=0\).

Приклад\(\PageIndex{11}\): When Can You Apply the Intermediate Value Theorem?

Для\(f(x)=1/x,f(−1)=−1<0\) і\(f(1)=1>0\). Чи можна зробити висновок, що\(f(x)\) має нуль в інтервалі\([−1,1]\)?

Рішення

Ні. Функція не є безперервним над\([−1,1]\). Теорема про проміжні значення тут не застосовується.

Вправа\(\PageIndex{5}\)

Показати, що\(f(x)=x^3−x^2−3x+1\) має нуль за інтервал\([0,1]\).

Підказка: Знайти\(f(0)\) і\(f(1)\). Застосуйте теорему про проміжні значення.

Відповідь: \(f(0)=1>0,\;f(1)=−2<0;\;f(x)\)безперервно закінчується\([0,1]\). Вона повинна мати нуль на цьому проміжку.

Ключові концепції

Щоб функція була безперервною в точці, вона повинна бути визначена в цій точці, її межа повинна існувати в точці, а значення функції в цій точці повинно дорівнювати значенню межі в цій точці.
Розриви можуть бути класифіковані як знімні, стрибки або нескінченні.
Функція є безперервною протягом відкритого інтервалу, якщо вона безперервна в кожній точці інтервалу. Він безперервний протягом замкнутого інтервалу, якщо він безперервний у кожній точці його внутрішньої частини і є безперервним у своїх кінцевих точках.
Теорема складеної функції стверджує: Якщо\(f(x)\) неперервна при L і\(\displaystyle \lim_{x→a}g(x)=L\), то\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L)\).

Теорема проміжних значень гарантує, що якщо функція є безперервною протягом замкнутого інтервалу, функція приймає кожне значення між значеннями у своїх кінцевих точках.

Глосарій

безперервність в точці: Функція\(f(x)\) є неперервною в точці\(a\) тоді і лише тоді, коли виконуються наступні три умови: (1)\(f(a)\) визначено, (2)\(\displaystyle \lim_{x→a}f(x)\) існує та (3)\(\displaystyle \lim{x→a}f(x)=f(a)\)

безперервність зліва: Функція є безперервною ліворуч при\(b\) if\(\displaystyle \lim_{x→b^−}f(x)=f(b)\)

спадкоємність з правого: Функція є безперервною праворуч,\(a\) якщо\(\displaystyle \lim_{x→a^+}f(x)=f(a)\)

безперервність протягом інтервалу: функція, яку можна простежити за допомогою олівця, не піднімаючи олівець; функція є безперервною протягом відкритого інтервалу, якщо вона безперервна в кожній точці інтервалу; функція\(f(x)\) є безперервною протягом замкнутого інтервалу форми [\(a,b\)] якщо вона безперервна в кожній точці в (\(a,b\)), і він безперервний з правого\(a\) і ліворуч на\(b\)

розрив у точці: Функція є переривчастою в точці або має розрив у точці, якщо вона не є безперервною в точці

нескінченний розрив: Нескінченний розрив відбувається в точці,\(a\) якщо\(\displaystyle \lim_{x→a^−}f(x)=±∞\) або\(\displaystyle \lim_{x→a^+}f(x)=±∞\)

Теорема про проміжні значення: \(f\)Дозволяти бути безперервним протягом замкнутого обмеженого інтервалу [\(a,b\)] якщо\(z\) будь-яке дійсне число між\(f(a)\) і\(f(b)\), то є число\(c\) в [\(a,b\)] задовольняє\(f(c)=z\)

стрибок розриву: Розрив стрибка відбувається в точці,\(a\) якщо\(\displaystyle \lim_{x→a^−}f(x)\) і\(\displaystyle \lim_{x→a^+}f(x)\) обидва існують, але\(\displaystyle \lim_{x→a^−}f(x)≠\lim_{x→a^+}f(x)\)

знімний розрив: Знімний розрив відбувається в точці,\(a\) якщо\(f(x)\) є переривчастим в\(a\), але\(\displaystyle \lim_{x→a}f(x)\) існує