2.2: Межа функції

Last updated
Save as PDF

Page ID: 62349

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Використовуючи правильні позначення, опишіть межу функції.
Використовуйте таблицю значень, щоб оцінити межу функції або визначити, коли ліміт не існує.
Використовуйте графік, щоб оцінити межу функції або визначити, коли ліміт не існує.
Визначте односторонні межі та наведіть приклади.
Поясніть взаємозв'язок між односторонніми і двосторонніми межами.
Використовуючи правильні позначення, опишіть нескінченну межу.
Визначте вертикальну асимптоту.

Поняття граничного або обмежувального процесу, важливе значення для розуміння обчислення, існує протягом тисяч років. Насправді ранні математики використовували обмежувальний процес для отримання кращих і кращих наближень областей кіл. Проте формальне визначення межі - як ми його знаємо і розуміємо сьогодні - з'явилося лише наприкінці 19 століття. Тому ми починаємо наше прагнення зрозуміти межі, як це робили наші математичні предки, використовуючи інтуїтивний підхід. В кінці цієї глави, озброївшись концептуальним розумінням меж, розглядаємо формальне визначення межі.

Ми починаємо наше дослідження меж з погляду на графіки функцій

\(f(x)=\dfrac{x^2−4}{x−2}\),
\(g(x)=\dfrac{|x−2|}{x−2}\), і
\(h(x)=\dfrac{1}{(x−2)^2}\),

які наведені на рис\(\PageIndex{1}\). Зокрема, давайте зосередимо нашу увагу на поведінці кожного графіка в районі та навколо нього\(x=2\).

Три графіки функцій. Перша - f (s) = (x^2 — 4)/(x-2), яка є лінією нахилу, x перехоплення (-2,0) та відкритого кола на (2,4). Другий - g (x) = |x — 2 |/(x-2), який містить два рядки: x=1 для x — Малюнок\(\PageIndex{1}\): Ці графіки показують поведінку трьох різних функцій навколо\(x=2\).

Кожна з трьох функцій не визначена на\(x=2\), але якщо ми робимо це твердження і ніякі інші, ми даємо дуже неповну картину того, як кожна функція поводиться в безпосередній близькості від\(x=2\). Щоб виразити поведінку кожного графа в околицях\(2\) більш повно, нам потрібно ввести поняття межі.

Інтуїтивне визначення межі

Давайте спочатку докладніше розглянемо, як\(f(x)=(x^2−4)/(x−2)\) поводиться функція навколо на\(x=2\) малюнку\(\PageIndex{1}\). Як значення\(x\)\(2\) наближаються з обох сторін\(2\), значення\(y=f(x)\) наближення\(4\). Математично ми говоримо, що\(f(x)\) межа як\(x\) підходів\(2\) є\(4\). Символічно ми виражаємо цю межу як

\(\displaystyle \lim_{x \to 2} f(x)=4\).

З цього дуже короткого неформального погляду на одну межу почнемо розробляти інтуїтивне визначення межі. Ми можемо думати, що\(a\) межа функції в числі є єдиним дійсним числом, до якого функціональні значення наближаються як підхід\(x\) -values\(a\), за умови,\(L\) що таке дійсне число\(L\) існує. Викладене більш ретельно, ми маємо наступне визначення:

Визначення (інтуїтивне): Обмеження

\(f(x)\)Дозволяти функція, визначена на всіх значеннях у відкритому інтервалі\(a\), що містить, з можливим винятком\(a\) себе, і нехай\(L\) бути дійсним числом. Якщо всі значення функції\(f(x)\) наближаються до дійсного числа\(L\) як значення\(x(≠a)\) наближення до числа\(a\), то ми говоримо, що межа\(f(x)\) як\(x\)\(a\) наближається є\(L\). (Більш стислий, як\(x\) наближається\(a\),\(f(x)\) наближається і залишається поруч\(L\).) Символічно ми висловлюємо цю ідею як

\[\lim_{x \to a} f(x)=L. \label{limit} \]

Ми можемо оцінити межі шляхом побудови таблиць функціональних значень і розглядаючи їх графіки. Цей процес описаний у наступній стратегії вирішення проблем.

Стратегія вирішення проблем: оцінка межі за допомогою таблиці функціональних значень

1. Для оцінки\(\displaystyle \lim_{x \to a} f(x)\) почнемо з заповнення таблиці функціональних значень. Ми повинні вибрати два набори\(x\) -values - один набір значень, що наближаються\(a\) і менше\(a\), а інший набір значень наближаються\(a\) і більше ніж\(a\). Таблиця\(\PageIndex{1}\) демонструє, як можуть виглядати ваші таблиці.

Таблиця\(\PageIndex{1}\)
\(x\)	\(f(x)\)	\(x\)	\(f(x)\)
\ (x\)» style="вирівнювання тексту: центр; ">\(a-0.1\)	\ (f (x)\)» style="вирівнювання тексту: центр; ">\(f(a-0.1)\)	\ (x\)» style="вирівнювання тексту: центр; ">\(a+0.1\)	\ (f (x)\)» style="вирівнювання тексту: центр; ">\(f(a+0.1)\)
\ (x\)» style="вирівнювання тексту: центр; ">\(a-0.01\)	\ (f (x)\)» style="вирівнювання тексту: центр; ">\(f(a-0.01)\)	\ (x\)» style="вирівнювання тексту: центр; ">\(a+0.01\)	\ (f (x)\)» style="вирівнювання тексту: центр; ">\(f(a+0.01)\)
\ (x\)» style="вирівнювання тексту: центр; ">\(a-0.001\)	\ (f (x)\)» style="вирівнювання тексту: центр; ">\(f(a-0.001)\)	\ (x\)» style="вирівнювання тексту: центр; ">\(a+0.001\)	\ (f (x)\)» style="вирівнювання тексту: центр; ">\(f(a+0.001)\)
\ (x\)» style="вирівнювання тексту: центр; ">\(a-0.0001\)	\ (f (x)\)» style="вирівнювання тексту: центр; ">\(f(a-0.0001)\)	\ (x\)» style="вирівнювання тексту: центр; ">\(a+0.0001\)	\ (f (x)\)» style="вирівнювання тексту: центр; ">\(f(a+0.0001)\)
\ (f (x)\)» rowspan="1" style="text-align:center; ">Використовуйте додаткові значення за необхідності.		\ (f (x)\)» rowspan="1" style="text-align:center; ">Використовуйте додаткові значення за необхідності.

2. Далі, давайте подивимося на значення в кожному з\(f(x)\) стовпців і визначимо, чи здається, значення наближаються до одного значення, коли ми рухаємося вниз кожного стовпця. У наших стовпцях ми дивимося на послідовність\(f(a−0.1)\)\(f(a−0.01)\)\(f(a−0.001)\),\(f(a−0.0001)\),,, і так далі\(f(a+0.1), \;f(a+0.01), \;f(a+0.001), \;f(a+0.0001)\), і так далі. (Примітка: Хоча ми вибрали\(x\) -values\(a±0.1, \;a±0.01, \;a±0.001, \;a±0.0001\), і так далі, і ці значення, ймовірно, працюватимуть майже кожен раз, в дуже рідкісних випадках нам може знадобитися змінити наш вибір.)

3. Якщо обидва стовпці наближаються до загального\(y\) -значення\(L\), ми констатуємо\(\displaystyle \lim_{x \to a}f(x)=L\). Ми можемо використовувати наступну стратегію для підтвердження результату, отриманого з таблиці або як альтернативний метод оцінки ліміту.

4. Використовуючи графічний калькулятор або комп'ютерне програмне забезпечення, яке дозволяє нам функції графа, ми можемо побудувати функцію\(f(x)\), переконавшись, що функціональні значення\(f(x)\) for\(x\) -values поруч\(a\) знаходяться в нашому вікні. Ми можемо використовувати функцію трасування для переміщення по графіку функції та спостерігати зчитування\(y\) -value як підхід\(x\) -values\(a\). Якщо\(y\) -значення наближаються\(L\) як наші\(x\) -значення\(a\) наближаються з обох напрямків, то\(\displaystyle \lim_{x \to a}f(x)=L\). Можливо, нам доведеться збільшити масштаб нашого графіка і повторити цей процес кілька разів.

Ми застосовуємо цю стратегію вирішення проблем для обчислення ліміту в прикладах\(\PageIndex{1A}\) і\(\PageIndex{1B}\).

Приклад\(\PageIndex{1A}\): Evaluating a Limit Using a Table of Functional Values

Оцініть\(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) за допомогою таблиці функціональних значень.

Рішення

Ми розрахували значення\(f(x)=\dfrac{\sin x}{x}\) для значень\(x\) перерахованих в табл\(\PageIndex{2}\).

Таблиця\(\PageIndex{2}\)
\(x\)	\(\frac{\sin x}{x}\)	\(x\)	\(\frac{\sin x}{x}\)
\ (x\)» style="вирівнювання тексту: центр; ">-0.1	\ (\ frac {\ sin x} {x}\)» style="вирівнювання тексту: центр; "> 0.998334166468	\ (x\)» style="вирівнювання тексту: центр; "> 0.1	\ (\ frac {\ sin x} {x}\)» style="вирівнювання тексту: центр; "> 0.998334166468
\ (x\)» style="вирівнювання тексту: центр; ">-0.01	\ (\ frac {\ sin x} {x}\)» style="вирівнювання тексту: центр; "> 0.999983333417	\ (x\)» style="вирівнювання тексту: центр; "> 0.01	\ (\ frac {\ sin x} {x}\)» style="вирівнювання тексту: центр; "> 0.999983333417
\ (x\)» style="вирівнювання тексту: центр; ">-0.001	\ (\ frac {\ sin x} {x}\)» style="вирівнювання тексту: центр; ">0.999999833333	\ (x\)» style="вирівнювання тексту: центр; "> 0.001	\ (\ frac {\ sin x} {x}\)» style="вирівнювання тексту: центр; ">0.999999833333
\ (x\)» style="вирівнювання тексту: центр; ">-0,0001	\ (\ frac {\ sin x} {x}\)» style="вирівнювання тексту: центр; "> 0.99999999998333	\ (x\)» style="вирівнювання тексту: центр; "> 0.0001	\ (\ frac {\ sin x} {x}\)» style="вирівнювання тексту: центр; "> 0.99999999998333

Примітка: Значення в цій таблиці були отримані за допомогою калькулятора і з використанням всіх місць, заданих у виході калькулятора.

Коли ми читаємо кожен\(\dfrac{\sin x}{x}\) стовпець, ми бачимо, що значення в кожному стовпці, здається, наближаються до одного. Таким чином, досить розумно зробити висновок про це\(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). Калькулятор або комп'ютерний графік\(f(x)=\dfrac{\sin x}{x}\) буде подібний до показаного на малюнку\(\PageIndex{2}\), і це підтверджує нашу оцінку.

Графік f (x) = sin (x) /x за інтервалом [-6, 6]. Функція викривлення має перехоплення y при x = 0 і x перехоплює при y = pi та y = -pi. — Малюнок\(\PageIndex{2}\): Графік\(f(x)=(\sin x)/x\) підтверджує кошторис з табл\(\PageIndex{2}\).

Приклад\(\PageIndex{1B}\): Evaluating a Limit Using a Table of Functional Values

Оцініть\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}\) за допомогою таблиці функціональних значень.

Рішення

Як і раніше, ми використовуємо таблицю — у цьому випадку Table\(\PageIndex{3}\) —щоб перерахувати значення функції для заданих значень\(x\).

Таблиця\(\PageIndex{3}\)
\(x\)	\(\frac{\sqrt{x}−2}{x−4}\)	\(x\)	\(\frac{\sqrt{x}−2}{x−4}\)
\ (x\)» style="вирівнювання тексту: центр; "> 3.9	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.251582341869	\ (x\)» style="вирівнювання тексту: центр; "> 4.1	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.248456731317
\ (x\)» style="вирівнювання тексту: центр; "> 3.99	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.25015644562	\ (x\)» style="вирівнювання тексту: центр; "> 4.01	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.24984394501
\ (x\)» style="вирівнювання тексту: центр; "> 3.999	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.250015627	\ (x\)» style="вирівнювання тексту: центр; "> 4.001	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.249984377
\ (x\)» style="вирівнювання тексту: центр; "> 3.9999	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.250001563	\ (x\)» style="вирівнювання тексту: центр; "> 4.0001	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.249998438
\ (x\)» style="вирівнювання тексту: центр; "> 3.99999	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.25000016	\ (x\)» style="вирівнювання тексту: центр; "> 4.00001	\ (\ frac {\ sqrt {x} −2} {x−4}\)» стиль="вирівнювання тексту: центр; ">0.24999984

Після огляду цієї таблиці ми бачимо, що функціональні значення менше 4, здається, зменшуються до 0,25, тоді як функціональні значення більше 4, здається, збільшуються до 0,25. Ми робимо висновок, що\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0.25\). Цю оцінку підтверджуємо за допомогою графіка,\(f(x)=\dfrac{\sqrt{x}−2}{x−4}\) показаного на малюнку\(\PageIndex{3}\).

Графік функції f (x) = (sqrt (x) — 2)/(x-4) за інтервал [0,8]. На функції є відкрите коло при x = 4. Функція крива асимптотично до осі x та осі y у квадранті. — Малюнок\(\PageIndex{3}\): Графік\(\frac{\sqrt{x}−2}{x−4}\) підтверджує кошторис з табл\(\PageIndex{3}\).

Вправа\(\PageIndex{1}\)

\(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\)Оцініть за допомогою таблиці функціональних значень. Використовуйте графік, щоб підтвердити свою оцінку.

Підказка: Використовуйте 0.9, 0.99, 0.999, 0.9999, 0.9999 і 1.1, 1.01, 1.001, 1.0001, 1.0001, 1.00001 в якості значень таблиці.
Відповідь: \[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\nonumber \]

На цьому етапі ми бачимо з прикладів,\(\PageIndex{1A}\) і\(\PageIndex{1b}\) що може бути так само просто, якщо не простіше, оцінити межу функції, оглянувши її графік, як і оцінити межу за допомогою таблиці функціональних значень. У прикладі\(\PageIndex{2}\) ми оцінюємо межу виключно шляхом перегляду графіка, а не за допомогою таблиці функціональних значень.

Приклад\(\PageIndex{2}\): Evaluating a Limit Using a Graph

Для\(g(x)\) показаних на\(\PageIndex{4}\) малюнку оцініть\(\displaystyle \lim_{x\to−1}g(x)\).

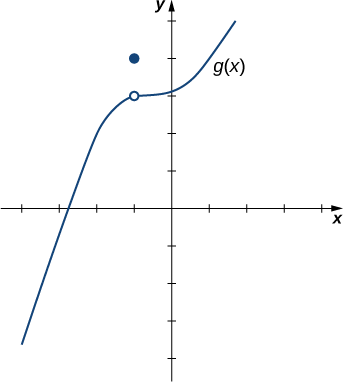
Графік загальної кривої функції g (x). У другому квадранті є розімкнуте коло на функції в (-1,3) і замкнуте коло на одиницю вгору при (-1, 4). — Малюнок\(\PageIndex{4}\): Графік\(g(x)\) включає одне значення не на гладкій кривій.

Рішення:

Незважаючи на те\(g(−1)=4\), що у міру наближення\(x\) -значення\(−1\) з будь-якого боку,\(g(x)\) значення наближаються\(3\). Тому,\(\displaystyle \lim_{x\to−1}g(x)=3\). Зауважте, що ми можемо визначити цю межу, навіть не знаючи алгебраїчного виразу функції.

На основі Прикладу ми робимо наступне спостереження: Можливо\(\PageIndex{2}\), щоб межа функції існувала в точці, а функція повинна бути визначена в цій точці, але межа функції і значення функції в точці можуть бути різними.

Вправа\(\PageIndex{2}\)

Використовуйте графік на\(h(x)\) малюнку\(\PageIndex{5}\) для оцінки\(\displaystyle \lim_{x \to 2}h(x)\), якщо це можливо.

Графік функції h (x), яка є параболою, розміщеною на графіку [-2.5, 5]. Існує відкрите коло, де вершина повинна знаходитися в точці (2, -1). — Малюнок\(\PageIndex{5}\):

Підказка: До чого\(y\) -value функція наближається як\(x\) -values наближається\(2\)?
Рішення: \(\displaystyle \lim_{x \to 2}h(x)=−1.\)

Погляд на таблицю функціональних значень або погляд на графік функції дає нам корисне уявлення про значення межі функції в заданій точці. Однак ці прийоми занадто сильно покладаються на здогадки. Зрештою нам потрібно розробити альтернативні методи оцінки лімітів. Ці нові методи мають більш алгебраїчний характер, і ми досліджуємо їх у наступному розділі; однак на цьому етапі ми вводимо два спеціальні обмеження, які є основоположними для майбутніх методів.

Дві важливі межі

\(a\)Дозволяти бути дійсним числом і\(c\) бути константою.

\(\displaystyle \lim_{x \to a}x=a\)
\(\displaystyle \lim_{x \to a}c=c\)

Ми можемо зробити наступні спостереження щодо цих двох меж.

Для першої межі дотримуйтесь, що як\(x\) наближається\(a\), так і робить\(f(x)\), тому що\(f(x)=x\). Отже,\(\displaystyle \lim_{x \to a}x=a\).
Для другого ліміту розглянемо табл\(\PageIndex{4}\).

Таблиця\(\PageIndex{4}\)
\(x\)	\(f(x)=c\)	\(x\)	\(f(x)=c\)
\ (x\)» style="вирівнювання тексту: центр; ">\(a-0.1\)	\ (f (x) = c\)» style="вирівнювання тексту: центр; ">\(c\)	\ (x\)» style="вирівнювання тексту: центр; ">\(a+0.1\)	\ (f (x) = c\)» style="вирівнювання тексту: центр; ">\(c\)
\ (x\)» style="вирівнювання тексту: центр; ">\(a-0.01\)	\ (f (x) = c\)» style="вирівнювання тексту: центр; ">\(c\)	\ (x\)» style="вирівнювання тексту: центр; ">\(a+0.01\)	\ (f (x) = c\)» style="вирівнювання тексту: центр; ">\(c\)
\ (x\)» style="вирівнювання тексту: центр; ">\(a-0.001\)	\ (f (x) = c\)» style="вирівнювання тексту: центр; ">\(c\)	\ (x\)» style="вирівнювання тексту: центр; ">\(a+0.001\)	\ (f (x) = c\)» style="вирівнювання тексту: центр; ">\(c\)
\ (x\)» style="вирівнювання тексту: центр; ">\(a-0.0001\)	\ (f (x) = c\)» style="вирівнювання тексту: центр; ">\(c\)	\ (x\)» style="вирівнювання тексту: центр; ">\(a+0.0001\)	\ (f (x) = c\)» style="вирівнювання тексту: центр; ">\(c\)

Зверніть увагу, що для всіх значень\(x\) (незалежно від того, наближаються вони\(a\)) значення\(f(x)\) залишаються постійними при\(c\). У нас немає іншого вибору, як зробити висновок\(\displaystyle \lim_{x \to a}c=c\).

Існування ліміту

Розглядаючи межу в наступному прикладі, майте на увазі, що для того, щоб межа функції існувала в точці, функціональні значення повинні наближатися до єдиного дійсного числа значення в цій точці. Якщо функціональні значення не наближаються до єдиного значення, то межі не існує.

Приклад\(\PageIndex{3}\): Evaluating a Limit That Fails to Exist

Оцініть\(\displaystyle\lim_{x \to 0}\sin(1/x)\) за допомогою таблиці значень.

Рішення

У таблиці\(\PageIndex{5}\) наведено значення функції\(\sin(1/x)\) для заданих значень\(x\).

Таблиця\(\PageIndex{5}\)
\(x\)	\(\sin(1/x)\)	\(x\)	\(\sin(1/x)\)
\ (x\)» style="вирівнювання тексту: центр; ">-0.1	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; "> 0.544021110889	\ (x\)» style="вирівнювання тексту: центр; "> 0.1	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; ">−0.544021110889
\ (x\)» style="вирівнювання тексту: центр; ">-0.01	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; "> 0.50636564111	\ (x\)» style="вирівнювання тексту: центр; "> 0.01	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; ">−0.50636564111
\ (x\)» style="вирівнювання тексту: центр; ">-0.001	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; ">−0.8268795405312	\ (x\)» style="вирівнювання тексту: центр; "> 0.001	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; "> 0.8268795405312
\ (x\)» style="вирівнювання тексту: центр; ">-0,0001	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; "> 0.305614388888	\ (x\)» style="вирівнювання тексту: центр; "> 0.0001	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; ">−0.305614388888
\ (x\)» style="вирівнювання тексту: центр; ">-0.00001	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; ">−0.035748797987	\ (x\)» style="вирівнювання тексту: центр; "> 0.00001	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; "> 0.035748797987
\ (x\)» style="вирівнювання тексту: центр; "> -0.000001	\ (\ sin (1/x)\)» стиль = «вирівнювання тексту: центр;" > 0.349993504187	\ (x\)» style="вирівнювання тексту: центр; "> 0.000001	\ (\ sin (1/x)\)» style="вирівнювання тексту: центр; ">−0.349993504187

Вивчивши таблицю функціональних значень, ми можемо побачити, що\(y\) -значення, здається, не наближаються до якогось одного єдиного значення. Виявляється, ліміту не існує. Перш ніж робити такий висновок, давайте більш системний підхід. Візьміть наступну послідовність наближаються\(x\) -значень\(0\):

\[\frac{2}{π},\;\frac{2}{3π},\;\frac{2}{5π},\;\frac{2}{7π},\;\frac{2}{9π},\;\frac{2}{11π},\;….\nonumber \]

Відповідними\(y\) -значеннями є

\[1,\;-1,\;1,\;-1,\;1,\;-1,\;....\nonumber \]

На цьому етапі ми дійсно можемо зробити висновок, що\(\displaystyle \lim_{x \to 0} \sin(1/x)\) не існує. (Математики часто скорочують «не існує» як DNE. Таким чином, ми б написали\(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE.) Графік\(f(x)=\sin(1/x)\) показаний на малюнку\(\PageIndex{6}\) і дає більш чітке уявлення про поведінку\(\sin(1/x)\) як\(x\) підходів\(0\). Ви можете бачити, що\(\sin(1/x)\) коливається все більш дико між\(−1\) і\(1\) як\(x\) підходи\(0\).

Графік функції f (x) = sin (1/x), яка швидко коливається між -1 і 1, коли х наближається до 0. Коливання менш часті, оскільки функція відходить від 0 на осі x. — Малюнок\(\PageIndex{6}\): Графік швидко\(f(x)=\sin (1/x)\) коливається між\(−1\) і\(1\) як\(x\) підходи\(0\).

Вправа\(\PageIndex{3}\)

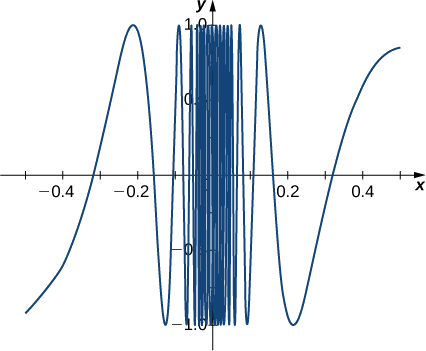
Використовуйте таблицю функціональних значень для оцінки\(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\), якщо це можливо.

Підказка: Використовуйте\(x\) -значення 1.9, 1.99, 1.999, 1.9999, 1.99999 та 2.1, 2.01, 2.001, 2.0001, 2.0001, 2.00001 у вашій таблиці.
Відповідь: \(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\)не існує.

Односторонні межі

Іноді вказівка на те, що межа функції не існує в точці, не дає нам достатньо інформації про поведінку функції в цій конкретній точці. Щоб переконатися в цьому, ми переглядаємо функцію,\(g(x)=|x−2|/(x−2)\) введену на початку розділу (див. Рисунок\(\PageIndex{1}\) (b)). Коли ми вибираємо значення\(x\) близьких до\(2\),\(g(x)\) не наближається до єдиного значення, тому межі як\(x\) підходів\(2\) не існує - тобто\(\displaystyle \lim_{x \to 2}g(x)\) DNE. Однак одне це твердження не дає нам повної картини поведінки функції навколо\(x\) -value\(2\). Щоб надати більш точний опис, введемо ідею одностороннього обмеження. Для всіх значень зліва від\(2\) (або негативної сторони\(2\)),\(g(x)=−1\). Таким чином, у міру\(x\)\(2\) наближення зліва,\(g(x)\) наближається\(−1\). Математично скажемо, що межа як\(x\) наближається\(2\) зліва є\(−1\). Символічно ми висловлюємо цю ідею як

\[\lim_{x \to 2^−}g(x)=−1. \nonumber \]

Аналогічно, як\(x\) підходи\(2\) з правого (або з позитивного боку),\(g(x)\) підходи\(1\). Символічно ми висловлюємо цю ідею як

\[\lim_{x \to 2^+}g(x)=1.\nonumber \]

Тепер ми можемо представити неформальне визначення односторонніх меж.

Визначення: Односторонні межі

Визначено два типи односторонніх меж.

Ліміт зліва:

\(f(x)\)Дозволяти бути функція, визначена на всіх значеннях у відкритому інтервалі форми\((z,a)\), і нехай\(L\) бути дійсним числом. Якщо значення функції\(f(x)\) наближаються до дійсного числа,\(L\) оскільки значення\(x\) (де\(x<a\)) наближаються до числа\(a\), то ми говоримо, що\(L\) це межа\(f(x)\) як\(x\) наближається\(a\) зліва. Символічно ми висловлюємо цю ідею як

\[\lim_{x \to a^−}f(x)=L. \nonumber \]

Обмеження праворуч:

\(f(x)\)Дозволяти бути функція, визначена на всіх значеннях у відкритому інтервалі форми\((a,c)\), і нехай\(L\) бути дійсним числом. Якщо значення функції\(f(x)\) наближаються до дійсного числа,\(L\) оскільки значення\(x\) (де\(x>a\)) наближаються до числа\(a\), то ми говоримо, що\(L\) це межа\(f(x)\) як\(x\) наближається\(a\) справа. Символічно ми висловлюємо цю ідею як

\[\lim_{x \to a^+}f(x)=L. \nonumber \]

Приклад\(\PageIndex{4}\): Evaluating One-Sided Limits

Для функції\(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\) оцініть кожне з наступних меж.

\(\displaystyle \lim_{x \to 2^−}f(x)\)
\(\displaystyle \lim_{x \to 2^+}f(x)\)

Рішення

Ми можемо знову використовувати таблиці функціональних значень. Зауважте в таблиці,\(\PageIndex{6}\) що для значень\(x\) менше\(2\), ми використовуємо\(f(x)=x+1\) і для значень\(x\) більше\(2\), ніж, ми використовуємо\(f(x)=x^2−4.\)

Таблиця\(\PageIndex{6}\)
\(x\)	\(f(x)=x+1\)	\(x\)	\(f(x)=x^2-4\)
\ (x\)» style="вирівнювання тексту: центр; "> 1.9	\ (f (x) =x+1\)» style="вирівнювання тексту: центр; "> 2.9	\ (x\)» style="вирівнювання тексту: центр; "> 2.1	\ (f (x) = x ^ 2-4\)» style="вирівнювання тексту: центр; "> 0.41
\ (x\)» style="вирівнювання тексту: центр; "> 1.99	\ (f (x) =x+1\)» style="вирівнювання тексту: центр; "> 2.99	\ (x\)» style="вирівнювання тексту: центр; "> 2.01	\ (f (x) = x ^ 2-4\)» style="вирівнювання тексту: центр; "> 0.0401
\ (x\)» style="вирівнювання тексту: центр; "> 1.999	\ (f (x) =x+1\)» style="вирівнювання тексту: центр; "> 2.999	\ (x\)» style="вирівнювання тексту: центр; "> 2.001	\ (f (x) = x ^ 2-4\)» style="вирівнювання тексту: центр; "> 0.004001
\ (x\)» style="вирівнювання тексту: центр; "> 1.9999	\ (f (x) =x+1\)» style="вирівнювання тексту: центр; "> 2.9999	\ (x\)» style="вирівнювання тексту: центр; "> 2.0001	\ (f (x) = x ^ 2-4\)» style="вирівнювання тексту: центр; "> 0.00040001
\ (x\)» style="вирівнювання тексту: центр; "> 1.99999	\ (f (x) =x+1\)» style="вирівнювання тексту: центр; "> 2.99999	\ (x\)» style="вирівнювання тексту: центр; "> 2.00001	\ (f (x) = x ^ 2-4\)» стиль = "вирівнювання тексту: центр; "> 0.000000400001

Виходячи з цієї таблиці, можна зробити висновок, що а.\(\displaystyle \lim_{x \to 2^−}f(x)=3\) і б\(\displaystyle \lim_{x \to 2^+}f(x)=0\). Тому (двостороння) межа\(f(x)\) не існує при\(x=2\). Малюнок\(\PageIndex{7}\) показує графік\(f(x)\) і підкріплює наш висновок про ці межі.

Графік заданої кускової функції. Перший шматок - f (x) = x+1, якщо x < 2. Другий шматок - x^2 — 4, якщо x — Малюнок\(\PageIndex{7}\): Графік\(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\) має перерву в\(x=2\).

Вправа\(\PageIndex{4}\)

Використовуйте таблицю функціональних значень, щоб оцінити наступні межі, якщо це можливо.

\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\)
\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}\)

Підказка

Для оцінки використовуйте\(x\) -значення 1.9, 1.99, 1.999, 1.9999, 1.99999\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\).

Використовуйте\(x\) значення 2.1, 2.01, 2.001, 2.0001, 2.0001, 2.00001 для оцінки\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}.\)

(Ці таблиці доступні з попередньої проблеми Checkpoint.)

Рішення a

а.\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}=−4\)

Рішення б

\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}=4\)

Давайте тепер розглянемо зв'язок між межею функції в точці та межами праворуч і ліворуч у цій точці. Здається зрозумілим, що якщо межа праворуч і межа зліва мають спільне значення, то це загальне значення є межею функції в цій точці. Аналогічно, якщо ліміт зліва і межа справа приймають різні значення, межі функції не існує. Ці висновки узагальнені в Примітці.

Пов'язані односторонній і двосторонній межі

\(f(x)\)Дозволяти функція, визначена на всіх значеннях у відкритому інтервалі\(a\), що містить, з можливим винятком\(a\) себе, і нехай\(L\) бути дійсним числом. Потім,

\[\lim_{x \to a}f(x)=L \nonumber \]

якщо і тільки якщо\(\displaystyle \lim_{x \to a^−}f(x)=L\) і\(\displaystyle \lim_{x \to a^+} f(x)=L\).

Нескінченні межі

Оцінка межі функції в точці або оцінка межі функції праворуч і ліворуч у точці допомагає нам охарактеризувати поведінку функції навколо заданого значення. Як ми побачимо, ми також можемо описати поведінку функцій, які не мають кінцевих меж.

Тепер звернемо увагу на те\(h(x)=1/(x−2)^2\), що третя і остання функція введена на початку цього розділу\(\PageIndex{1}\) (див. Рис. З його графіка ми бачимо, що в міру\(x\)\(2\) наближення значення\(h(x)=1/(x−2)^2\) стають все більшими і більшими і, по суті, стають нескінченними. Математично ми говоримо, що\(h(x)\) межа як\(x\) підходів\(2\) - позитивна нескінченність. Символічно ми висловлюємо цю ідею як

\[\lim_{x \to 2}h(x)=+∞. \nonumber \]

Більш загально, ми визначаємо нескінченні межі наступним чином:

Визначення: Нескінченні межі

Визначимо три типи нескінченних меж.

Нескінченні межі зліва: Дозволяти\(f(x)\) бути функцією, визначеною у всіх значеннях у відкритому інтервалі форми\((b,a)\).

i. якщо значення\(f(x)\) збільшення без прив'язки як значення\(x\) (де\(x<a\)) наближаються до числа\(a\), то скажемо, що межа як\(x\) наближається\(a\) зліва позитивна нескінченність і пишемо\[\lim_{x \to a^−}f(x)=+∞. \nonumber \]

II. Якщо значення\(f(x)\) зменшення без прив'язки як значення\(x\) (де\(x<a\)) наближаються до числа\(a\), то скажемо, що межа як\(x\) наближається\(a\) зліва негативна нескінченність і пишемо\[\lim_{x \to a^−}f(x)=−∞. \nonumber \]

Нескінченні межі праворуч:\(f(x)\) Дозволяти бути функцією, визначеною у всіх значеннях у відкритому інтервалі форми\((a,c)\).

i. якщо значення\(f(x)\) збільшення без прив'язки як значення\(x\) (де\(x>a\)) наближаються до числа\(a\), то скажемо, що межа як\(x\) наближається\(a\) справа - позитивна нескінченність і пишемо\[\lim_{x \to a^+}f(x)=+∞. \nonumber \]

II. Якщо значення\(f(x)\) зменшення без прив'язки як значення\(x\) (де\(x>a\)) наближаються до числа\(a\), то скажемо, що межа як\(x\) наближається\(a\) справа негативна нескінченність і пишемо\[\lim_{x \to a^+}f(x)=−∞. \nonumber \]

Двосторонній нескінченний межа: Дозвольте\(f(x)\) бути визначено для всіх\(x≠a\) у відкритому інтервалі, що містить\(a\)

i. якщо значення\(f(x)\) збільшення без прив'язки як значення\(x\) (де\(x≠a\)) наближаються до числа\(a\), то скажемо, що межа як\(x\)\(a\) наближається позитивна нескінченність і пишемо\[\lim_{x \to a} f(x)=+∞. \nonumber \]

II. Якщо значення\(f(x)\) зменшення без прив'язки як значення\(x\) (де\(x≠a\)) наближаються до числа\(a\), то скажемо, що межа як\(x\)\(a\) наближається негативна нескінченність і пишемо\[\lim_{x \to a}f(x)=−∞. \nonumber \]

Важливо розуміти, що коли ми пишемо такі заяви, як\(\displaystyle \lim_{x \to a}f(x)=+∞\) або\(\displaystyle \lim_{x \to a}f(x)=−∞\) ми описуємо поведінку функції, як ми щойно її визначили. Ми не стверджуємо, що межа існує. \(f(x)\)Щоб межа функції існувала на\(a\), вона повинна наближатися до дійсного числа\(L\) як\(x\) підходи\(a\). Тим не менш, якщо, наприклад\(\displaystyle \lim_{x \to a}f(x)=+∞\), ми завжди пишемо,\(\displaystyle \lim_{x \to a}f(x)=+∞\) а\(\displaystyle \lim_{x \to a}f(x)\) не DNE.

Приклад\(\PageIndex{5}\): Recognizing an Infinite Limit

Оцініть кожен з наступних обмежень, якщо це можливо. Використовуйте таблицю функціональних значень і графік,\(f(x)=1/x\) щоб підтвердити свій висновок.

\(\displaystyle \lim_{x \to 0^−} \frac{1}{x}\)
\(\displaystyle \lim_{x \to 0^+} \frac{1}{x}\)
\( \displaystyle \lim_{x \to 0}\frac{1}{x}\)

Рішення

Почніть з побудови таблиці функціональних значень.

Таблиця\(\PageIndex{7}\)
\(x\)	\(\dfrac{1}{x}\)	\(x\)	\(\dfrac{1}{x}\)
\ (x\)» style="вирівнювання тексту: центр; ">-0.1	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">-10	\ (x\)» style="вирівнювання тексту: центр; "> 0.1	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">10
\ (x\)» style="вирівнювання тексту: центр; ">-0.01	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">-100	\ (x\)» style="вирівнювання тексту: центр; "> 0.01	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">100
\ (x\)» style="вирівнювання тексту: центр; ">-0.001	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">-1000	\ (x\)» style="вирівнювання тексту: центр; "> 0.001	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">1000
\ (x\)» style="вирівнювання тексту: центр; ">-0,0001	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">-10,000	\ (x\)» style="вирівнювання тексту: центр; "> 0.0001	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">10,000
\ (x\)» style="вирівнювання тексту: центр; ">-0.00001	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">-100 000	\ (x\)» style="вирівнювання тексту: центр; "> 0.00001	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">100,000
\ (x\)» style="вирівнювання тексту: центр; "> -0.000001	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; ">-1,000,000	\ (x\)» style="вирівнювання тексту: центр; "> 0.000001	\ (\ dfrac {1} {x}\)» style="вирівнювання тексту: центр; "> 1,000,000

а Значення\(1/x\) зменшення без прив'язки як\(x\) підходи\(0\) зліва. Ми робимо висновок, що

\[\lim_{x \to 0^−}\frac{1}{x}=−∞.\nonumber \]

б. значення\(1/x\) збільшення без прив'язки як\(x\) наближається\(0\) справа. Ми робимо висновок, що

\[\lim_{x \to 0^+}\frac{1}{x}=+∞. \nonumber \]

c Оскільки\(\displaystyle \lim_{x \to 0^−}\frac{1}{x}=−∞\) і\(\displaystyle \lim_{x \to 0^+}\frac{1}{x}=+∞\) мають різні значення, робимо висновок, що

\[\lim_{x \to 0}\frac{1}{x}\quad\text{DNE.} \nonumber \]

Графік на\(f(x)=1/x\) малюнку\(\PageIndex{8}\) підтверджує ці висновки.

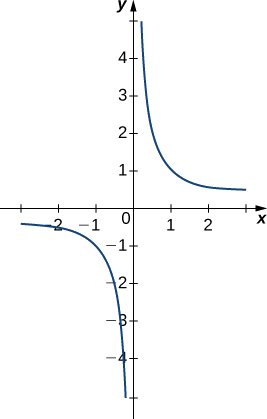
Графік функції f (x) = 1/x, криві функції асимптотично до x=0 та y=0 у квадратах один і три. — Малюнок\(\PageIndex{8}\): Графік\(f(x)=1/x\) підтверджує, що межі як\(x\) підходів\(0\) не існує.

Вправа\(\PageIndex{5}\)

Оцініть кожен з наступних обмежень, якщо це можливо. Використовуйте таблицю функціональних значень і графік,\(f(x)=1/x^2\) щоб підтвердити свій висновок.

\(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}\)
\(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}\)
\(\displaystyle \lim_{x \to 0}\frac{1}{x^2}\)

Підказка

Дотримуйтесь процедур з Прикладу\(\PageIndex{5}\).

Відповідь

а.\(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}=+∞\);

б.\(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}=+∞\);

c.\(\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+∞\)

Корисно зазначити, що функції виду\(f(x)=1/(x−a)^n\), де n - натуральне ціле число, мають нескінченні межі як\(x\) підходи\(a\) зліва, так і справа (рис.\(\PageIndex{9}\)). Ці межі узагальнені в вищевказаних визначеннях.

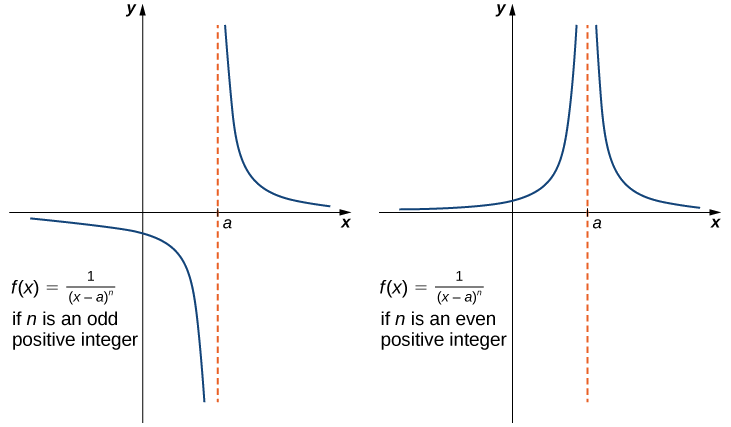
Два графіки поруч з f (x) = 1/(x-a) ^n. Перший графік показує випадок, коли n - непарне натуральне число, а другий показує випадок, коли n - парне натуральне число. У першому графік має два відрізки. Кожна крива асимптотично до осі x, також відома як y=0, і x = a. відрізок зліва від x = a знаходиться нижче осі x, а відрізок праворуч від x = a знаходиться над віссю x. На другому графіку обидва сегменти знаходяться над віссю x. — Малюнок\(\PageIndex{9}\): Функція\(f(x)=1/(x−a)^n\) має нескінченні межі на\(a\).

Нескінченні межі від позитивних цілих чисел

Якщо\(n\) є додатним парним числом, то

\[\lim_{x \to a}\frac{1}{(x−a)^n}=+∞.\label{infLim1} \]

Якщо\(n\) є додатним непарним числом, то

\[\lim_{x \to a^+}\frac{1}{(x−a)^n}=+∞\label{infLim2} \]

\[\lim_{x \to a^−}\frac{1}{(x−a)^n}=−∞.\label{infLim3} \]

Слід також зазначити, що на графіках точки на графіку\(f(x)=1/(x−a)^n\), що мають\(x\)\(a\) -координати дуже близько до вертикальної лінії\(x=a\). Тобто в міру\(x\)\(a\) наближення точки на графіку\(f(x)\) розташовуються ближче до лінії\(x=a\). Лінія\(x=a\) називається вертикальною асимптотою графа. Формально визначимо вертикальну асимптоту наступним чином:

Визначення: Вертикальні асимптоти

\(f(x)\)Дозволяти бути функцією. Якщо будь-яка з наведених нижче умов дотримується, то лінія\(x=a\) є вертикальною асимптотою\(f(x)\).

\[\lim_{x \to a^−}f(x)=+∞ \nonumber \]

\[\lim_{x \to a^−}f(x)=−∞ \nonumber \]

\[\lim_{x \to a^+}f(x)=+∞ \nonumber \]

\[\lim_{x \to a^+}f(x)=−∞ \nonumber \]

\[\lim_{x \to a}f(x)=+∞ \nonumber \]

\[\lim_{x \to a}f(x)=−∞ \nonumber \]

Приклад\(\PageIndex{6}\): Finding a Vertical Asymptote

Оцініть кожне з наведених нижче меж за допомогою рівнянь\ ref {InFliM1},\ ref {InfLim2} та\ ref {InfLim3} вище. Визначте будь-які вертикальні асимптоти функції\(f(x)=1/(x+3)^4.\)

\(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}\)
\(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}\)
\(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}\)

Рішення

Ми можемо використовувати вищевказані рівняння безпосередньо.

\(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}=+∞\)
\(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}=+∞\)
\(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}=+∞\)

Функція\(f(x)=1/(x+3)^4\) має вертикальну асимптоту\(x=−3\).

Вправа\(\PageIndex{6}\)

Оцініть кожне з наступних обмежень. Визначте будь-які вертикальні асимптоти функції\(f(x)=\dfrac{1}{(x−2)^3}\).

\(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}\)
\(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}\)
\(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)

Відповідь на: \(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}=−∞\)
Відповідь б: \(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}=+∞\)
Відповідь c: \(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)ДНЕ. Лінія\(x=2\) - вертикальна асимптота\(f(x)=1/(x−2)^3.\)

У наступному прикладі ми поклали наші знання про різні типи обмежень для аналізу поведінки функції в декількох різних точках.

Приклад\(\PageIndex{7}\): Behavior of a Function at Different Points

Використовуйте графік на\(f(x)\) малюнку,\(\PageIndex{10}\) щоб визначити кожне з наступних значень:

\(\displaystyle \lim_{x \to −4^−}f(x)\)\(\displaystyle \lim_{x \to −4^+}f(x)\);\(\displaystyle \lim_{x→−4}f(x);\;f(−4)\)
\(\displaystyle \lim_{x \to −2^−}f(x\))\(\displaystyle \lim_{x \to −2^+}f(x)\);\(\displaystyle \lim_{x→−2}f(x);\;f(−2)\)
\( \displaystyle \lim_{x \to 1^−}f(x)\)\(\displaystyle \lim_{x \to 1^+}f(x)\);\(\displaystyle \lim_{x \to 1}f(x);\;f(1)\)
\( \displaystyle \lim_{x \to 3^−}f(x)\)\(\displaystyle \lim_{x \to 3^+}f(x)\);\(\displaystyle \lim_{x \to 3}f(x);\;f(3)\)

Графік функції f (x) описується вищевказаними межами і значеннями. Існує плавна крива для значень нижче x=-2; при (-2, 3) - розімкнута коло. Існує плавна крива між (-2, 1] із замкнутим колом на (1,6). Існує відкрите коло в (1,3), і плавна крива, що тягнеться звідти вниз асимптотично до негативної нескінченності вздовж x = 3. Функція також крива асимптотично вздовж x = 3 з іншого боку, також розтягуючись до негативної нескінченності. Потім функція змінює увігнутість у першому квадранті навколо y = 4.5 і продовжує вгору. — Малюнок\(\PageIndex{10}\): Графік показує\(f(x)\).

Рішення

Використовуючи наведені вище визначення та графік для довідки, ми приходимо до наступних значень:

\(\displaystyle \lim_{x \to −4^−}f(x)=0\)\(\displaystyle \lim_{x \to −4^+}f(x)=0\);\(\displaystyle \lim_{x \to −4}f(x)=0;\;f(−4)=0\)
\(\displaystyle \lim_{x \to −2^−}f(x)=3\);\(\displaystyle \lim_{x \to −2^+}f(x)=3\);\(\displaystyle \lim_{x \to −2}f(x)=3;\;f(−2)\) не визначено
\(\displaystyle \lim_{x \to 1^−}f(x)=6\);\(\displaystyle \lim_{x \to 1^+}f(x)=3\);\(\displaystyle \lim_{x \to 1}f(x)\) ДНЄ;\(f(1)=6\)
\(\displaystyle \lim_{x \to 3^−}f(x)=−∞\);\(\displaystyle \lim_{x \to 3^+}f(x)=−∞\);\(\displaystyle \lim_{x \to 3}f(x)=−∞\);\(f(3)\) не визначено

Вправа\(\PageIndex{7}\)

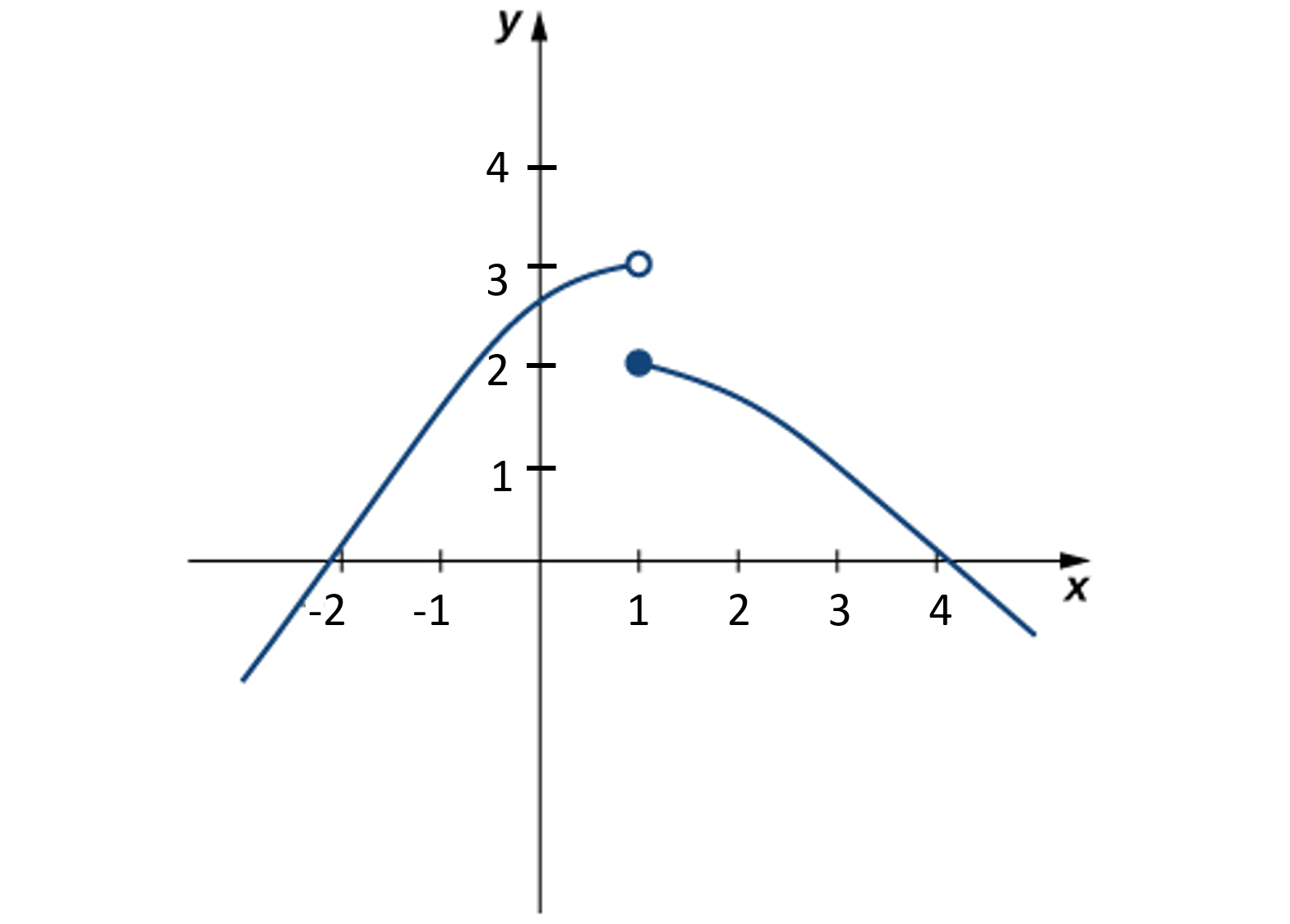
Оцініть\(\displaystyle\lim_{x \to 1}f(x)\) для\(f(x)\) показаних тут:

Графік кускової функції. Перший відрізок вигинається від третього квадранта до першого, перетинаючись через другий квадрант. Там, де кінцева точка буде в першому квадранті - це відкрите коло. Другий відрізок починається з замкнутого кола на кілька одиниць нижче відкритого кола. Він кривий вниз від одного квадранта до четвертого квадранта. — Малюнок\(\PageIndex{11}\). Графік кускової функції\(f\).

Підказка: Порівняйте ліміт справа з лімітом зліва.
Відповідь: \(\displaystyle\lim_{x \to 1}f(x)\)не існує

Приклад\(\PageIndex{8}\): Einstein’s Equation

У відкритті глави ми коротко згадали, як Альберт Ейнштейн показав, що існує межа того, наскільки швидко будь-який об'єкт може подорожувати. Дано рівняння Ейнштейна для маси рухомого об'єкта

\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]

яка цінність цього прив'язки?

Зображення футуристичного космічного корабля, що проходить через глибокий космос. — Малюнок\(\PageIndex{12}\). (Кредит: NASA)

Рішення

Нашою відправною точкою є рівняння Ейнштейна для маси рухомого об'єкта,

\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]

де\(m_0\) маса об'єкта в спокої,\(v\) - його швидкість, а\(c\) це швидкість світла. Щоб побачити, як змінюється маса на високих швидкостях, ми можемо скласти графік співвідношення мас\(m/m_0\) як функція співвідношення швидкостей,\(v/c\) (рис.\(\PageIndex{13}\)).

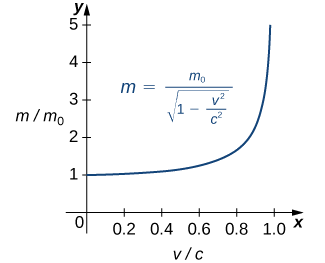
Графік, що показує співвідношення мас як функцію співвідношення швидкості в рівнянні Ейнштейна для маси рухомого об'єкта. Вісь х - відношення швидкостей, v/c Вісь y - відношення мас, м/м0. Рівняння функції m = m0/sqrt (1 — v2/c2). Графік знаходиться тільки в квадранті 1. Він починається з (0,1) і плавно вигинається приблизно до 0,8, де він збільшується, здавалося б, експоненціально; існує вертикальна асимптота при v/c (або x) = 1. — Малюнок\(\PageIndex{13}\): Цей графік показує співвідношення мас як функція співвідношення швидкостей в рівнянні Ейнштейна для маси рухомого об'єкта.

Ми бачимо, що у міру наближення співвідношення швидкостей 1 — тобто, коли швидкість об'єкта наближається до швидкості світла - співвідношення мас збільшується без обмежень. Іншими словами, функція має вертикальну асимптоту при\(v/c=1\). Ми можемо спробувати кілька значень цього співвідношення, щоб перевірити цю ідею.

Таблиця\(\PageIndex{8}\)
\(v/c\)	\(\sqrt{1-\frac{v^2}{c^2}}\)	\(m/m_o\)
\ (v/c\)» style="вирівнювання тексту: центр; "> 0.99	\ (\ sqrt {1-\ frac {v^2} {c^2}}\)» стиль ="вирівнювання тексту: центр; ">0.1411	\ (m/m_o\)» style="вирівнювання тексту: центр; "> 7.089
\ (v/c\)» style="вирівнювання тексту: центр; "> 0.999	\ (\ sqrt {1-\ frac {v^2} {c^2}}\)» стиль = "вирівнювання тексту: центр; ">0.0447	\ (m/m_o\)» style="вирівнювання тексту: центр; "> 22.37
\ (v/c\)» style="вирівнювання тексту: центр; "> 0.9999	\ (\ sqrt {1-\ frac {v^2} {c^2}}\)» стиль ="вирівнювання тексту: центр; ">0.0141	\ (m/m_o\)» style="вирівнювання тексту: центр; "> 70.7

Так, згідно з табл.\(\PageIndex{8}\): якщо об'єкт масою 100 кг їде при 0,9999c, його маса стає 7071 кг. Оскільки жоден об'єкт не може мати нескінченну масу, ми робимо висновок, що жоден об'єкт не може подорожувати зі швидкістю світла або більше.

Ключові поняття

Для оцінки ліміту може використовуватися таблиця значень або графік.
Якщо межі функції в точці не існує, все одно можливо, що межі зліва і справа в цій точці можуть існувати.
Якщо межі функції зліва і справа існують і рівні, то межа функції - це загальне значення.
Ми можемо використовувати обмеження для опису нескінченної поведінки функції в точці.

Ключові рівняння

Інтуїтивне визначення межі

\(\displaystyle \lim_{x \to a}f(x)=L\)

Дві важливі межі

\(\displaystyle \lim_{x \to a}x=a \qquad \lim_{x \to a}c=c\)

Односторонні межі

\(\displaystyle \lim_{x \to a^−}f(x)=L \qquad \lim_{x \to a^+}f(x)=L\)

Нескінченні межі зліва

\(\displaystyle \lim_{x \to a^−}f(x)=+∞ \qquad \lim_{x \to a^−} f(x)=−∞\)

Нескінченні межі з правого

\(\displaystyle \lim_{x \to a^+}f(x)=+∞ \qquad \lim_{x \to a^+} f(x)=−∞\)

Двосторонні нескінченні межі

\(\displaystyle \lim_{x \to a}f(x)=+∞\):\(\displaystyle \lim_{x \to a^−}f(x)=+∞\) і\(\displaystyle \lim_{x \to a^+} f(x)=+∞\)

\(\displaystyle \lim_{x \to a}f(x)=−∞\):\(\displaystyle \lim_{x \to a^−}f(x)=−∞\) і\(\displaystyle \lim_{x \to a^+} f(x)=−∞\)

Глосарій

нескінченна межа: Функція має нескінченну межу в точці,\(a\) якщо вона або збільшується або зменшується без обмежень у міру наближення.\(a\)

інтуїтивне визначення ліміту: Якщо всі значення функції\(f(x)\) наближаються до дійсного числа\(L\) як значення\(x(≠a)\) наближення a,\(f(x)\) наближається до L

одностороння межа: Одностороння межа функції - це межа, взята з лівого або правого

вертикальна асимптота: Функція має вертикальну асимптоту,\(x=a\) якщо межа\(x\)\(a\) наближення праворуч або ліворуч нескінченна.