11.5: Параметр довжини дуги та кривизна

У звичайній розмові ми описуємо позицію як з точки зору часу, так і відстані. Наприклад, уявіть, як їздити в гості до друга. Якщо вона зателефонує і запитає, де ви знаходитесь, ви можете відповісти: «Я за 20 хвилин від вашого будинку», або ви можете сказати: «Я в 10 милі від вашого будинку». Обидві відповіді дають вашому другові загальне уявлення про те, де ви знаходитесь.

В даний час наші векторні функції мають визначені точки з параметром$t$, який ми часто приймаємо для представлення часу. Розглянемо Малюнок$\PageIndex{1a}$, де$\vecs r (t) = \langle t^2-t,t^2+t\rangle$ зображено графіки і точки, відповідні$t=0,\ 1$ і$2$ показані. Зверніть увагу, як довжина дуги між$t=0$ і$t=1$ менше, ніж довжина дуги між$t=1$ і$t=2$; якщо$t$ параметр - час і$\vecs r$ положення, ми можемо сказати, що частка пройшла швидше,$[1,2]$ ніж на$[0,1]$.

Малюнок$\PageIndex{1}$: Введення параметра довжини дуги.

Тепер розглянемо Малюнок$\PageIndex{1b}$, де один і той же графік параметризується іншою змінною$s$. Наносяться точки$s=6$, відповідні$s=0$ наскрізному. Довжина дуги графіка між кожною сусідньою парою точок дорівнює 1. Ми можемо розглядати цей параметр$s$ як відстань; тобто довжина дуги графіка від$s=0$ до$s=3$ дорівнює 3, довжина дуги від$s=2$ до$s=6$ дорівнює 4 і т.д. якщо потрібно знайти точку 2.5 одиниць від початкового місця (тобто$s=0$), можна буде обчислити$\vecs r(2.5)$. Цей параметр$s$ дуже корисний, і називається параметром довжини дуги.

Як ми знаходимо параметр довжини дуги?

Почніть з будь-якої параметризації$\vecs r$. Ми можемо обчислити довжину дуги графіка$\vecs r$ на інтервалі$[0,t]$ з $$\text{arc length } = \int_0^t\norm{\vecs r\,'(u)} du.$$ Ми можемо перетворити це в функцію: як$t$ змінюється, ми знаходимо довжину дуги$s$ від$0$ до$t$. Ця функція є

$$s(t) = \int_0^t \norm{\vecs r\,'(u)} du.\label{eq:vvfarc}$$

Це встановлює взаємозв'язок між$s$ і$t$. Знаючи цей зв'язок явно, ми можемо переписати$\vecs r(t)$ як функцію$s$:$\vecs r(s)$. Ми демонструємо це на прикладі.

Приклад$\PageIndex{1}$: Finding the arc length parameter

Нехай$\vecs r(t) = \langle 3t-1,4t+2\rangle$. Параметризуйте$\vecs r$ параметром довжини дуги$s$.}

Рішення

Використовуючи рівняння\ ref {eq:vvfarc}, запишемо

$$s(t) = \int_0^t \norm{\vecs r\,'(u)} du. \nonumber$$

Ми можемо інтегрувати це, явно знаходячи зв'язок між$s$ і$t$:

\ [\ почати {align*}
s (t) &=\ int_0^t\ норма {\ векс r\, '(u)} ду\\ [4pt]
&=\ int_0^t\ sqrt {3^2+4^2} ду\\ [4pt]
&=\ int_0^t 5 ду\\ [4pt]
&= 5t.
\ end {вирівнювати*}\]

Так як$s=5t$, ми можемо записати$t=s/5$ і$\vecs r(t)$ замінити$t$ в на$s/5$:

$$\vecs r(s) = \langle 3(s/5)-1, 4(s/5)+2\rangle = \langle \dfrac35s-1,\dfrac45s+2\rangle. \nonumber$$

Зрозуміло, що як показано на малюнку$\PageIndex{2}$, графік$\vecs r$ є лінією, де$t=0$ відповідає точка$(-1,2)$. Яка точка на лінії знаходиться на відстані 2 одиниць від цієї початкової точки? Знаходимо його с$s(2) = \langle 1/5, 18/5\rangle$.

Малюнок$\PageIndex{2}$: Графік$vec{r}$ у прикладі$\PageIndex{1}$.

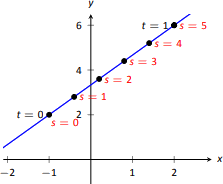
Чи$(1/5,18/5)$ дійсно точка 2 одиниць далеко від$(-1,2)$? Використовуємо формулу відстані для перевірки:

$$\begin{align*} d &= \sqrt{\left(\dfrac15-(-1)\right)^2+ \left(\dfrac{18}5-2\right)^2} \\[4pt] &= \sqrt{\dfrac{36}{25}+\dfrac{64}{25}} \\[4pt] = \sqrt{4}=2. \end{align*}$$

Так,$s(2)$ дійсно 2 одиниці відстані, у напрямку руху, від початкової точки.

Речі спрацювали дуже добре в прикладі$\PageIndex{1}$; ми змогли встановити безпосередньо, що$s=5t$. Зазвичай параметр довжини дуги набагато складніше описати з точки зору$t$, в результаті інтеграції квадратного кореня. Є ряд речей, які ми можемо дізнатися про параметр довжини дуги з Equation\ ref {eq:vvfarc}, однак, які є неймовірно корисними.

Спочатку візьміть похідне$s$ по відношенню до$t$. Фундаментальна теорема числення (див. Теорема 39) стверджує, що

$$\dfrac{ds}{dt}=s\,'(t) = \norm{\vecs r ^\prime(t)}.\label{eq:vvfarc3}$$

Дозволяючи$t$$\vecs r(t)$ представляти час і представляти позицію, ми бачимо, що швидкість зміни щодо швидкості; тобто швидкість зміни «пройденої відстані» - це швидкість, яка повинна відповідати нашій інтуїції.$s$$t$

Правило ланцюга стверджує, що

\ [\ почати {вирівнювати*}
\ dfrac {d\ vecs r} {dt} &=\ dfrac {d\ vecs r} {ds}\ cdot\ dfrac {dt}\ [4pt]\ vecs r ^
\ прайм (т) &=\ vecs r ^\ прайм (s)\ cdot\ норма {\ vecs r ^\ прайм (т))}.
\ end {вирівнювати*}\]

Вирішуючи для$\vecs r ^\prime(s)$, ми маємо

$$\vecs r ^\prime(s) = \dfrac{\vecs r ^\prime(t)}{\norm{\vecs r ^\prime(t)}} = \vecs T(t),\label{eq:vvfarc2}$$

де$\vecs T(t)$ - одиничний тангенс вектора. Рівняння\ ref {eq:vvfarc2} часто неправильно інтерпретується, оскільки виникає спокуса думати$\vecs r ^\prime(t) = \vecs T(t)$, що воно стверджує, але існує велика різниця між$\vecs r ^\prime(s)$ і$\vecs r ^\prime(t)$. Ключ, який потрібно взяти з нього, полягає в тому, що$\vecs r ^\prime(s)$ є одиничним вектором. Насправді наступна теорема стверджує, що це характеризує параметр довжини дуги.

Теорема 99: Параметр довжини дуги

$\vecs r(s)$Дозволяти бути векторно-значною функцією. Параметр$s$ є параметром довжини дуги якщо, і тільки якщо,$\norm{\vecs r ^\prime(s)} = 1.$

викривлення

Розглянемо точки$A$ і$B$ на кривій, зображеній на малюнку$\PageIndex{3a}$. Можна з легкістю стверджувати, що крива крива більш різко при$A$, ніж при$B$. Корисно використовувати число, щоб описати, наскільки різко крива згинається; це число є кривизною кривої.

Малюнок$\PageIndex{3}$: Встановлення поняття кривизни.

Виводимо це число наступним чином. Розглянемо Малюнок$\PageIndex{3b}$, де одиничні дотичні вектори графуються навколо точок$A$ і$B$. Зверніть увагу, як напрямок вектора дотичної одиниці змінюється зовсім трохи поблизу$A$, тоді як він не змінюється так сильно навколо$B$. Це призводить до важливого поняття: вимірювання швидкості зміни одиничного тангенса вектора по відношенню до довжини дуги дає нам вимір кривизни.

Визначення$\PageIndex{1}$: Curvature

$\vecs r(s)$Дозволяти векторно-значною функцією, де$s$ є параметр довжини дуги. $\kappa$Кривизна графіка$\vecs r(s)$ є

$$\kappa = \norm{\dfrac{d\vecs T}{ds}} = \norm{\vecs T\,'(s)}.$$

Якщо$\vecs r(s)$ параметризується параметром довжини дуги, то

$$\vecs T(s) = \dfrac{\vecs r ^\prime(s)}{\norm{\vecs r ^\prime(s)}} \quad \text{and}\quad \vecs N(s) = \dfrac{\vecs T\,'(s)}{\norm{\vecs T\,'(s)}}.$$

Визначившись$\norm{\vecs T\,'(s)} =\kappa$, ми можемо переписати друге рівняння як

$$\vecs T\,'(s) = \kappa\vecs N(s).\label{eq:curvature}$$

Ми вже знали, що$\vecs T\,'(s)$ знаходиться в тому ж напрямку, що і$\vecs N(s)$; тобто ми можемо думати про те$\vecs T(s)$, що «витягується» у напрямку$\vecs N(s)$. Наскільки «важко» його тягнуть? За фактором$\kappa$. Коли кривизна велика,$\vecs T(s)$ то «тягне важко» і напрямок швидко$\vecs T(s)$ змінюється. Коли$\kappa$ маленький, не тягне$T(s)$ сильно і, отже, його напрямок не змінюється швидко.

Ми використовуємо Definition,$\PageIndex{1}$ щоб знайти кривизну лінії в прикладі$\PageIndex{2}$.

Приклад$\PageIndex{2}$: Finding the curvature of a line

Використовуйте Definition,$\PageIndex{1}$ щоб знайти кривизну$\vecs r (t) = \langle 3t-1,4t+2\rangle$.

Рішення

У прикладі\ ref {ex_vvfarc1} ми виявили, що параметр довжини дуги був визначений таким чином$\vecs r(s) =\langle 3t/5-1, 4t/5+2\rangle$ параметризований$\vecs r$ параметром довжини дуги.$s=5t$ Щоб знайти$\kappa$, нам потрібно знайти$\vecs T\,'(s)$.

$$\begin{align*} \vecs T(s) &= \vecs r ^\prime(s)\quad \text{(recall this is a unit vector)}\\[4pt]&= \langle 3/5, 4/5\rangle.\end{align*}$$

Тому

$$\vecs T\,'(s) = \langle 0,0\rangle \nonumber$$

і

$$\kappa=\norm{\vecs T\,'(s)} = 0. \nonumber$$

Ймовірно, не дивно, що кривизна лінії дорівнює 0. (Як «пишна» лінія? Це зовсім не пишні.)

Хоча визначення кривизни є прекрасним математичним поняттям, майже неможливо використовувати більшу частину часу; писати з$\vecs r$ точки зору параметра довжини дуги, як правило, дуже важко. На щастя, існують і інші методи обчислення цієї величини, які набагато простіше. Існує компроміс: визначення «легко» зрозуміти, хоча важко обчислити, тоді як ці інші формули легко обчислити, хоча це може бути важко зрозуміти, чому вони працюють.

теорема 100: Формули для кривизни

$C$Дозволяти бути плавна крива на відкритому інтервалі$I$ в площині або в просторі.

1. Якщо$C$ визначається шляхом$y=f(x)$, то $$\kappa = \dfrac{|f^{\prime\prime}(x)|}{\Big(1+\big(f^\prime (x)\big)^2\Big)^{3/2}}.$$
2. Якщо$C$ визначається як векторно-значна функція в площині$\vecs r(t) = \langle x(t), y(t)\rangle$, то $$\kappa = \dfrac{|x^\prime y^{\prime\prime}-x^{\prime\prime}y^{\prime} |}{\big((x^\prime )^2+(y^{\prime} )^2\big)^{3/2}}.$$
3. Якщо$C$ визначається в просторі векторно-значною функцією$\vecs r(t)$, то $$\kappa = \dfrac{\norm{\vecs T\,'(t)}}{\norm{\vecs r^\prime(t)}} = \dfrac{\norm{\vecs r^\prime(t)\times\vecs r^{\prime\prime}(t)}}{\norm{\vecs r^\prime(t)}^3} = \dfrac{\vecs a(t)\cdot \vecs N(t)}{\norm{\vecs v(t)}^2}.$$

Практикуємо використання цих формул.

Приклад$\PageIndex{3}$: Finding the curvature of a circle

Знайти кривизну окружності з радіусом$r$, визначеним$\vecs c(t) = \langle r\cos t,r\sin t\rangle$.

Рішення

Перш ніж почати, слід очікувати, що кривизна кола буде постійною, а не залежною від$t$. (Чому?)

Обчислюємо за$\kappa$ допомогою другої частини Теореми 100.

\ [\ почати {вирівнювати*}
\ каппа &=\ dfrac {| (-r\ sin t) (-r\ sin t) - (-r\ cos t) (r\ cos t) |} {\ big (-r\ sin t) ^2+ (r\ cos t) ^ {3/2}}\\ [4pt]
&=\ dfrac {r^2 (\ sin^2t+\ cos^2t)} {\ великий (r^2 (\ sin^2t+\ cos^2t)\ великий) ^ {3/2}}\\ [4пт]
&=\ dfrac {r^2} {r^3} =\ dfrac1r.
\ end {вирівнювати*}\]

Ми виявили, що коло з радіусом$r$ має кривизну$\kappa = 1/r$.

Приклад$\PageIndex{3}$ дає відмінний результат. Перед цим прикладом, якби нам сказали: «Крива має кривизну 5 в точці»$A$, ми б не мали уявлення, що це насправді означало. Чи 5 «великий» - чи відповідає дійсно різкий поворот, або не дуже різкий поворот? Тепер ми можемо думати про 5 через коло з радіусом 1/5. Знання одиниць (дюйми проти миль, наприклад) дозволяє нам визначити, наскільки різко крива викривляється.

Нехай точка$P$ на гладкій кривій$C$ буде задана, і$\kappa$ нехай кривизна кривої в$P$. Коло, яке:

• проходить наскрізь$P$,
• лежить на увігнутій стороні$C$,
• має загальну дотичну лінію, як$C$ at$P$ і
• має радіус$r=1/\kappa$ (отже, має кривизну$\kappa$)

це оскулюючий коло, або коло кривизни, до$C$ at$P$, і$r$ є радіусом кривизни. На малюнку$\PageIndex{4}$ показаний графік кривої, показаний раніше на малюнку 11.30, і її оскулюючі кола при$A$ і$B$. Різкий поворот відповідає окружності з малим радіусом; поступовий поворот відповідає окружності з великим радіусом. Вміти думати про кривизну з точки зору радіуса кола дуже корисно.

Малюнок 11.30

Приклад$\PageIndex{4}$: Finding curvature

Знайти кривизну параболи,$y=x^2$ визначену у вершині і в$x=1$.

Рішення

Використовуємо першу формулу, знайдену в теоремі 100.

\ [\ почати {вирівнювати*}
\ каппа (x) &=\ dfrac {|2|} {\ великий (1+ (2x) ^2\ великий) ^ {3/2}}\\ [4pt]
&=\ dfrac2 {\ великий (1+4x^2\ великий) ^ {3/2}}.
\ end {вирівнювати*}\]

Малюнок$\PageIndex{5}$: Вивчення кривизни$y=x^2$.

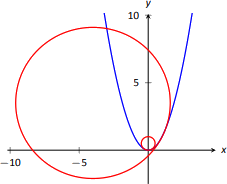
На вершині ($x=0$) кривизна є$\kappa = 2$. В$x=1$, кривизна є$\kappa = 2/(5)^{3/2} \approx 0.179.$ Таким чином$x=0$, кривизна$y=x^2$ - це окружність радіуса$1/2$; в$x=1$, кривизна - це коло з радіусом$\approx 1/0.179 \approx 5.59$. Це проілюстровано на малюнку$\PageIndex{5}$. В$x=3$, кривизна є$0.009$; графік майже прямий, оскільки кривизна дуже близька до 0.

Приклад$\PageIndex{5}$: Finding curvature

Знайдіть, де кривизна$\vecs r(t) = \langle t, t^2, 2t^3\rangle$ максимізована.


Розв'язок Ми використовуємо третю формулу в теоремі 100$\vecs r (t)$ як визначено в просторі. Ми залишаємо це читачеві, щоб переконатися, що

$$\vecs r ^\prime(t) =\langle 1,2t,6t^2\rangle,\quad \vecs r^{\prime\prime}(t) = \langle 0,2,12t\rangle,\quad \text{and}\quad \vecs r ^\prime(t)\times \vecs r^{\prime\prime}(t) = \langle 12t^2,-12t,2\rangle.$$

Малюнок$\PageIndex{6}$: Розуміння кривої кривої в просторі.

Таким чином

\ [\ почати {вирівнювати*}
\ каппа (t) &=\ dfrac {\ норма {\ векс r ^\ прайм (t)\ час\ векс r^ {\ прайм\ прайм} (t)}} {\ norm {\ vecs r ^\ прайм (t)} ^3}\ [4pt]
&=\ dfrac {\ норма {\ langle 12^t2, -12t,2\ діапазон}} {\ норма {\ кут 1,2t^2\ діапазон} ^3}\ [4pt]
&=\ dfrac {\ sqrt {144t^4+144t^2+4}} {\ ліворуч (\ sqrt {1+4t^2+36t^4\}\ праворуч) ^3}
\ end {align*}\]

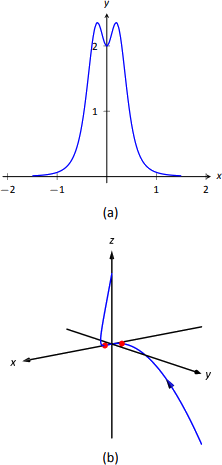
Хоча це не особливо «приємна» формула, вона явно говорить нам, що кривизна при заданому$t$ значенні. Щоб максимізувати$\kappa(t)$, ми повинні вирішити$\kappa'(t)=0$ для$t$. Це здійсненне, але дуже трудомістке. Замість цього розглянемо графік,$\kappa(t)$ як наведено на малюнку$\PageIndex{6a}$. Ми бачимо, що$\kappa$ максимізується при двох$t$ значеннях; використовуючи числовий розв'язувач, ми знаходимо ці значення є$t\approx\pm 0.189$. На малюнку$\PageIndex{1b}$ ми графуємо$\vecs r (t)$ і вказуємо точки, де кривизна максимізована.

Кривизна і рух

$\vecs r(t)$Дозволяти функція положення об'єкта, зі швидкістю$\vecs v (t) = \vecs r ^\prime(t)$ і прискоренням$\vecs a(t)=\vecs r^{\prime\prime}(t)$. У розділі 11.4 ми встановили, що прискорення знаходиться в площині,$\vecs T(t)$ утвореній і$\vecs N(t)$, і що ми можемо знайти скаляри$a_\text{T}$ і$a_\text{N}$ такі, що

$$\vecs a (t) = a_\text{T}\vecs T(t) + a_\text{N}\vecs N(t).$$

Теорема 98 дає формули для$a_\text{T}$ і$a_\text{N}$:

$$a_\text{T} = \dfrac{d}{dt}\Big(\norm{\vecs v (t) }\Big) \quad \text{and} \quad a_\text{N} = \dfrac{\norm{\vecs v (t) \times \vecs a (t) }}{\norm{\vecs v (t) }}.$$

Ми зрозуміли, що величина прискорення в напрямку$\vecs T$ відноситься тільки до того, як змінюється швидкість об'єкта, і що величина прискорення в напрямку на$\vecs N$ відноситься до того, як змінюється напрямок руху об'єкта. (Тобто, якщо об'єкт рухається з постійною швидкістю$a_\text{T}=0$; якщо об'єкт рухається в постійному напрямку,$a_\text{N}=0$.)

У Рівнянні\ ref {eq:vvfarc3} на початку цього розділу ми знайшли$s\,'(t) = \norm{\vecs v (t) }$. Ми можемо поєднати цей факт з вищевказаною формулою$a_\text{T}$ для запису

$$a_\text{T} = \dfrac{d}{dt}\Big(\norm{\vecs v (t) }\Big) = \dfrac{d}{dt}\big( s\,'(t)\big) = s\,''(t).$$

Оскільки$s\,'(t)$ це швидкість,$s\,''(t)$ це швидкість, з якою швидкість змінюється по відношенню до часу. Ми бачимо ще раз, що складова прискорення в напрямку руху відноситься тільки до швидкості, а не до зміни напрямку.

Тепер порівняйте формулу для$a_\text{N}$ вище з формулою кривизни в теоремі 100:

$$a_\text{N} = \dfrac{\norm{\vecs v (t) \times \vecs a (t) }}{\norm{\vecs v (t) }}\quad \text{and}\quad \kappa = \dfrac{\norm{\vecs r ^\prime(t)\times\vecs r^{\prime\prime}(t)}}{\norm{\vecs r ^\prime(t)}^3}=\dfrac{\norm{\vecs v (t) \times \vecs a (t) }}{\norm{\vecs v (t) }^3} .$$

Таким чином

\ [\ почати {вирівняти}
a_\ текст {N} &=\ каппа\ норма {\ vecs v (t)} ^2\ мітка {eq:curvature_an}\\ [4pt]
&=\ каппа\ Великий (s\, '(t)\ Великий) ^2\ nonumber
\ end {вирівнювання}\]

Це останнє рівняння показує, що компонент прискорення, який змінює напрямок об'єкта, залежить від двох речей: кривизни шляху та швидкості об'єкта.

Уявіть собі водіння автомобіля по колу годинникової стрілки. Ви, природно, відчуєте силу, що штовхає вас до дверей (точніше, двері штовхають вас, коли машина повертається, і ви хочете подорожувати по прямій лінії). Якщо ви тримаєте радіус кола постійним, але прискорюєте (тобто збільшуєте$s\,'(t)$), двері сильніше штовхається проти вас ($a_\text{N}$збільшилася). Якщо ви тримаєте свою швидкість постійною, але затягнете поворот (тобто збільшуєте$\kappa$), знову двері буде сильніше штовхнути проти вас.

Збираючи наші нові формули для$a_\text{T}$ та$a_\text{N}$ разом, ми маємо

$$\vecs a (t) = s\,''(t)\vecs T(t) + \kappa\norm{\vecs v (t) }^2\vecs N(t).$$

Це не особливо практичний спосіб пошуку$a_\text{T}$ і$a_\text{N}$, але він розкриває деякі чудові поняття про те, як прискорення взаємодіє зі швидкістю та формою кривої.

Приклад$\PageIndex{6}$: Curvature and road design

Мінімальний радіус кривої конюшини в шосе визначається робочою швидкістю, як наведено в таблиці на рис$\PageIndex{7}$. Для кожної кривої і швидкості обчислюйте$a_\text{N}$.

Малюнок$\PageIndex{7}$: Робоча швидкість та мінімальний радіус у конструкції конюшини шосе.

Рішення

Використовуючи Equation\ ref {eq:curvature_an}, ми можемо обчислити прискорення нормаль до кривої в кожному випадку. Ми починаємо з перетворення кожної швидкості з «миль на годину» в «фути в секунду» шляхом множення на$5280/3600$.

\ [\ почати {вирівнювати*}
\ текст {35 миль/год, 310 футів} &\ Стрілка вправо 51.33\ текст {ft/s},\ квад\ каппа = 1/310\\ [4pt]
a_\ текст {N} &=\ каппа\\\ норма {\ vecs v (t)} ^2\\ [4pt] &=\ dfrac1 {310}\ norm {\ vecs v (t)} ^2\\ [4pt]
&=\ dfrac1 {310}\ великий (51.1 33\ великий) ^2\\ [4pt]
&= 8.50\ текст {ft/s} ^2.
\ end {вирівнювати*}\]

\ [\ почати {вирівнювати*}
\ текст {40 миль/год, 430 футів} &\ Стрілка вправо 58.67\ текст {ft/s},\ квад\ каппа = 1/430\\ [4pt]
a_\ текст {N} &=\ dfrac1 {430}\ великий (58.67\ великий) ^2\\ [4pt]
&= 8.00\ текст {ft/s} ^2.
\ end {вирівнювати*}\]

\ [\ почати {вирівнювати*}
\ текст {45mph,540ft} &\ Стрілка вправо 66\ текст {ft/s},\ квад\ каппа = 1/540\\ [4pt]
a_\ текст {N} &=\ dfrac1 {540}\ великий (66\ великий) ^2\ [4pt]
&= 8.07\ текст {ft/s} ^2.
\ end {вирівнювати*}\]

Зверніть увагу, що кожне прискорення схоже; це за конструкцією. З огляду на класичну формулу «$\times$Прискорення сили$=$ масового прискорення», це прискорення необхідно тримати невеликим, щоб шини транспортного засобу тримали «зчеплення» з дорогою. Якщо хтось подорожує на повороті радіуса 310 футів зі швидкістю 50 км/год, прискорення подвійне, на 17.35 футів/с$^2$. Якщо розгін занадто високий, сили тертя, створюваної шинами, може виявитися недостатньо, щоб утримати автомобіль від ковзання. Інженери-будівельники регулярно обчислюють «безпечну» проектну швидкість, а потім віднімають 5-10mph, щоб створити розміщене обмеження швидкості для додаткової безпеки.

Ми закінчуємо цю главу роздумом про те, що ми охопили. Ми почали з векторно-значних функцій, які, можливо, здавалися в той час просто ще одним способом написання параметричних рівнянь. Однак ми бачили, що векторна перспектива дала нам велике уявлення про поведінку функцій та вивчення руху. Векторно-значні функції положення передають інформацію про переміщення, пройдену відстань, швидкість, швидкість, прискорення і кривизну, кожна з яких має велике значення в науці та техніці.