11.4: Одиничний тангенс і нормальний вектори

Одиниця тангенс вектор

З огляду на гладку векторно-значну функцію\(\vecs r(t)\), ми визначили у Визначенні 71, що будь-який паралельний вектору\(\vecs r^\prime(t_0)\) є дотичним до графа\(\vecs r (t)\) at\(t=t_0\). Часто корисно враховувати саме напрямок,\(\vecs r^\prime(t)\) а не його величину. Тому нас цікавить одиничний вектор в сторону\(\vecs r^\prime(t)\). Це призводить до визначення.

Визначення\(\PageIndex{1}\): Unit Tangent Vector

\(\vecs r (t)\)Дозволяти гладкою функцією на відкритому інтервалі\(I\). Одиничний тангенс\(\vecs T(t)\) вектора

\[\vecs T(t) = \dfrac{1}{\norm{\vecs r^\prime(t)}}\vecs r^\prime(t).\]

Приклад\(\PageIndex{1}\): Computing the unit tangent vector

Нехай\(\vecs r (t) = \langle 3\cos t, 3\sin t, 4t\rangle\). Знайти\(\vecs T(t)\) і обчислити\(\vecs T(0)\) і\(\vecs T(1)\).

Рішення

Застосовуємо Визначення\(\PageIndex{1}\), щоб знайти\(\vecs T(t)\).

\ [\ почати {вирівнювати*}
\ векс T (t) &=\ dfrac {1} {\ норма {\ vecs r^\ прайм (t)}}\ векс r^\ правий (t)\\ [4pt]
&=\ dfrac {1} {\ sqrt {\ лівий (-3\ sin t\ праворуч) ^2+\ лівий (3\ cos t\ правий) ^2+\ лівий (3\ cos t\ правий) 2+ 4^2}}\ ланголь -3\ sin t,3\ cos t, 4\ діапазон\\ [4pt]
&=\ ланголь -\ dfrac35\ sin t,\ dfrac35\ cos t,\ dfrac 45\ діапазон.
\ end {вирівнювати*}\]

Тепер ми можемо легко обчислити\(\vecs T(0)\) і\(\vecs T(1)\):

\[\begin{align*} \vecs T(0) &= \langle 0,\dfrac35,\dfrac45\rangle\, \\[4pt] \vecs T(1) &= \langle -\dfrac35\sin 1,\dfrac35\cos 1,\dfrac45\rangle \approx \langle -0.505,0.324,0.8\rangle.\end{align*}\]

Вони побудовані на малюнку\(\PageIndex{1}\) з їх початковими точками в\(\vecs r(0)\) і\(\vecs r(1)\), відповідно. (Вони виглядають досить «короткими», оскільки вони мають лише довжину 1.)

Малюнок\(\PageIndex{1}\): Побудова одиничних дотичних векторів у прикладі\(\PageIndex{1}\).

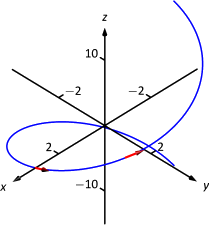
Вектор дотичної одиниці\(\vecs T(t)\) завжди має величину 1, хоча іноді легко сумніватися, що це правда. Ми можемо допомогти зміцнити цю думку в нашій свідомості, обчислюючи\(\norm{\vecs T(1)}\):

\[\norm{\vecs T(1)} \approx \sqrt{(-0.505)^2+0.324^2+0.8^2} = 1.000001. \nonumber\]

Ми округлили в нашому обчисленні\(\vecs T(1)\), так що ми не отримуємо 1 точно. Ми залишаємо читачеві використовувати точне подання,\(\vecs T(1)\) щоб переконатися, що воно має довжину 1.

Багато в чому попередній приклад був «занадто приємним». Виявилося, що завжди\(\vecs r^\prime(t)\) була довжини 5. У наступному прикладі довжина змінна, залишаючи нам формулу, яка не така чиста.\(\vecs r^\prime(t)\)

Приклад\(\PageIndex{2}\): Computing the unit tangent vector

Нехай\(\vecs r (t)=\langle t^2-t,t^2+t\rangle\). Знайти\(\vecs T(t)\) і обчислити\(\vecs T(0)\) і\(\vecs T(1)\).

Рішення

Ми знаходимо\(\vecs r^\prime(t) = \langle 2t-1,2t+1\rangle\), і

\[\norm{\vecs r^\prime(t)} = \sqrt{(2t-1)^2+(2t+1)^2} = \sqrt{8t^2+2}.\]

Тому

\[\vecs T(t) = \dfrac{1}{\sqrt{8t^2+2}}\langle 2t-1,2t+1\rangle = \langle \dfrac{2t-1}{\sqrt{8t^2+2}},\dfrac{2t+1}{\sqrt{8t^2+2}}\rangle.\]

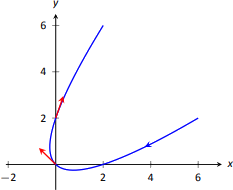
Коли\(t=0\), ми маємо\(\vecs T(0) = \langle -1/\sqrt{2},1/\sqrt{2}\rangle\); коли\(t=1\), ми маємо Ми\(\vecs T(1) = \langle 1/\sqrt{10}, 3/\sqrt{10}\rangle.\) залишаємо це читачеві, щоб переконатися, що кожен з них є одиничним вектором. Вони нанесені на рис\(\PageIndex{2}\).

Малюнок\(\PageIndex{2}\): Побудова одиничних дотичних векторів у прикладі\(\PageIndex{2}\).

Одиниця нормального вектора

Подібно до того, як важливо знати напрямок дотичної до шляху, важливо знати напрямок, ортогональний до шляху. При роботі з реальними функціями ми визначили нормальну лінію в точці бути лінією через точку, яка була перпендикулярна дотичній лінії в цій точці. Ми можемо зробити подібну річ з векторно-значними функціями. Задано\(\vecs r (t)\) в\(\mathbb{R}^2\), ми маємо 2 напрямки, перпендикулярні дотичному вектору, як показано на малюнку\(\PageIndex{3}\). Добре задатися питанням: «Чи є один з цих двох напрямків кращим перед іншим?»

Малюнок\(\PageIndex{3}\): Враховуючи напрямок у площині, завжди є два ортогональні до нього напрямки.

Задано\(\vecs r (t)\) в\(\mathbb{R}^3\), є нескінченні вектори, ортогональні дотичному вектору в заданій точці. Знову ж таки, ми можемо задатися питанням: «Чи є один з цих нескінченних варіантів кращим перед іншими? Чи є один з них «правильний» вибір?»

Відповідь в обох\(\mathbb{R}^2\) і\(\mathbb{R}^3\) є «Так, є один вектор, який є не тільки кращим, це «правильний» вибір». Нагадаємо Теорему 93, яка стверджує, що якщо\(\vecs r (t)\) має постійну довжину,\(\vecs r (t)\) то\(\vecs r^\prime(t)\) ортогональна для всіх\(t\). Ми знаємо\(\vecs T(t)\), що одиничний тангенс вектор, має постійну довжину. Тому\(\vecs T(t)\) є ортогональним до\(\vecs T\,'(t)\).

Ми побачимо, що\(\vecs T\,'(t)\) це більше, ніж просто зручний вибір вектора, який ортогональний\(\vecs r^\prime(t)\); скоріше, це «правильний» вибір. Оскільки все, що нас хвилює, - це напрямок, ми визначаємо цей щойно знайдений вектор як одиничний вектор.

Примітка:\(\vecs T(t)\) це одиничний вектор, за визначенням. Це не означає, що\(\vecs T\,'(t)\) це також одиничний вектор.

Визначення\(\PageIndex{2}\): Unit Normal Vector

\(\vecs r (t)\)Дозволяти векторно-значна функція, де дотичний вектор одиниці\(\vecs T(t)\), гладкий на відкритому інтервалі\(I\). Одиничний\(\vecs N(t)\) нормальний вектор

\[\vecs N(t) = \dfrac1{\norm{\vecs T\,'(t)}}\vecs T\,'(t).\]

Приклад\(\PageIndex{3}\): Computing the unit normal vector

Нехай\(\vecs r (t) = \langle 3\cos t, 3\sin t, 4t\rangle\) як у прикладі 11.4.1. Намалюйте обидва\(\vecs T(\pi/2)\) і\(\vecs N(\pi/2)\) з початковими точками на\(\vecs r(\pi/2)\).

Рішення

У\(\PageIndex{1}\) прикладі ми знайшли\(\vecs T(t) = \langle (-3/5)\sin t,(3/5)\cos t,4/5\rangle\). Тому

\[\vecs T\,'(t) = \langle -\dfrac35\cos t,-\dfrac35\sin t,0\rangle\quad \text{and} \quad \norm{\vecs T\,'(t)} = \dfrac35.\]

Таким чином

\[\vecs N(t) = \dfrac{\vecs T\,'(t)}{3/5} = \langle -\cos t,-\sin t,0\rangle.\]

Обчислюємо\(\vecs T(\pi/2) = \langle -3/5,0,4/5\rangle\) і\(\vecs N(\pi/2) = \langle 0,-1,0\rangle\). Вони намальовані на малюнку\(\PageIndex{4}\).

Рисунок\(\PageIndex{4}\): Побудова одиничних дотичних і нормальних векторів у прикладі\(\PageIndex{3}\).

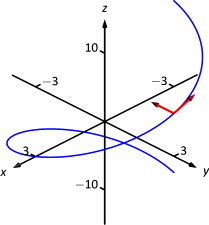
Попередній приклад знову був «занадто приємним». Загалом, вираз for\(\vecs T(t)\) містить частки квадратних коренів, отже, вираз\(\vecs T\,'(t)\) дуже безладно. Ми демонструємо це в наступному прикладі.

Приклад\(\PageIndex{4}\): Computing the unit normal vector

Нехай\(\vecs r (t)=\langle t^2-t,t^2+t\rangle\) як у прикладі\(\PageIndex{2}\). Знайдіть\(\vecs N(t)\) і намалюйте\(\vecs r (t)\) з одиничними дотичними і нормальними векторами в\(t=-1,0\) і 1.

Рішення

У\(\PageIndex{2}\) прикладі ми знайшли

\[\vecs T(t) = \langle \dfrac{2t-1}{\sqrt{8t^2+2}},\dfrac{2t+1}{\sqrt{8t^2+2}}\rangle.\]

Пошук\(\vecs T\,'(t)\) вимагає двох застосувань правила частки:

\ [\ почати {вирівнювати*}
T (t) &=\ ланголь\ dfrac {\ sqrt {8t^2+2} (2) - (2t-1)\ ліворуч (\ dfrac12 (8t^2+2) ^ {-1/2} (16t)\ праворуч)} {8t^2+2},\\ [4pt]
&\ quad\ dfrac {\ sqrt 8t^2+2} (2) - (2т+1)\ ліворуч (\ dfrac12 (8t^2+2) ^ {-1/2} (16t)\ праворуч)} {8t^2+2}\ діапазон\\ [4pt]
&=\ кут\ dfrac {4 (2 t+1)} {\ ліворуч (8 t^2+2\ праворуч) ^ {3/2}},\ dfrac {4 (1-2 т)} {\ ліворуч (8 t^2+2\ праворуч) ^ {3/2}}\ діапазон
\ end {align*}\]

Це не одиничний вектор; щоб знайти\(\vecs N(t)\), нам потрібно розділити\(\vecs T\,'(t)\) на його величину.

\ [\ почати {вирівнювати*}
\ норма {\ векс Т\, '(t)} &=\ sqrt {\ dfrac {16 (2т+1) ^2} {(8т^2+2) ^3} +\ dfrac {16 (1-2t) ^2} {(8t^2+2) ^3}}\ [4pt]
&=\ sqrt {\ dфракція {16 (8t^2+2)} {(8t^2+2) ^3}}\\ [4pt]
&=\ dfrac {4} {8t^2+2}.
\ end {вирівнювати*}\]

Нарешті,

\ [\ почати {вирівнювати*}
\ векс N (t) &=\ dfrac1 {4/ (8t^2+2)}\ кут\ dfrac {4 (2 t+1)} {\ лівий (8 t^2+2\ праворуч) ^ {3/2}},\ dfrac {4
(1-2 т)} {\ лівий (8 t^2+2\ праворуч) ^ {3/2}}\ діапазон\\ [4pt]
&=\ кут\ dfrac {2t+1} {\ sqrt {8t^2+2}}, -\ dfrac {2t-1} {\ sqrt {8t^2+2}}\ діапазон.
\ end {вирівнювати*}\]

Використовуючи цю формулу для\(\vecs N(t)\), обчислюємо одиничний тангенс і нормальний вектори для\(t=-1,0\) і 1 і намалюємо їх на рис\(\PageIndex{5}\).

Рисунок\(\PageIndex{5}\): Побудова одиничних дотичних і нормальних векторів у прикладі\(\PageIndex{4}\).

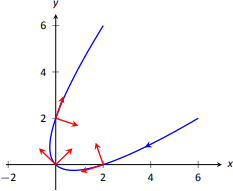
Кінцевий результат для\(\vecs N(t)\) в Приклад\(\PageIndex{4}\) підозріло схожий на\(\vecs T(t)\). Для цього є чітка причина. Якщо\(\vecs u = \langle u_1,u_2\rangle \) є одиничним вектором в\(\mathbb{R}^2\), то єдиними одиничними векторами,\(\vecs u\) ортогональними є\(\langle -u_2,u_1\rangle \) і\(\langle u_2,-u_1\rangle\). З огляду на\(\vecs T(t)\), ми можемо швидко визначити,\(\vecs N(t)\) чи знаємо ми, на який термін помножити\((-1)\).

Розглянемо ще раз малюнок 11.24, де ми побудували деякі одиничні дотичні і нормальні вектори. Зверніть увагу, як\(\vecs N(t)\) завжди вказує «всередині» кривої, або на увігнуту сторону кривої. Це не випадковість, це вірно в цілому. Знання напрямку, яке\(\vecs r(t)\) «повертає», дозволяє нам швидко знайти\(\vecs N(t)\).

ТЕОРЕМА\(\PageIndex{1}\): Unit Normal Vectors in \(\mathbb{R}^2\)

\(\vecs r(t)\)Дозволяти векторної функції в\(\mathbb{R}^2\) де\(\vecs T\,'(t)\) є гладкою на відкритому інтервалі\(I\). Дозвольте\(t_0\) бути в,\(I\) а\(\vecs T(t_0) = \langle t_1,t_2\rangle\) потім\(\vecs N(t_0)\) є або

\[\vecs N(t_0) = \langle -t_2,t_1\rangle \quad \text{or}\quad \vecs N(t_0) = \langle t_2,-t_1\rangle,\]

залежно від того, що є вектором, який вказує на увігнуту сторону графа\(\vecs r\).

Додаток до прискорення

\(\vecs r (t)\)Дозволяти функція положення. Це факт (викладено пізніше в теоремі\(\PageIndex{2}\)), що прискорення,\ vecs a (t), лежить в площині, визначеній\(\vecs T\) і\(\vecs N\). Тобто існують скаляри\(a_{\text{T}}\) і\(a_{\text{N}}\) такі, що

\[\vecs a (t) = a_{\text{T}}\vecs T(t) + a_{\text{N}}\vecs N(t).\]

Скаляр\(a_{\text{T}}\) вимірює «скільки» прискорення в напрямку руху, тобто вимірює складову прискорення, що впливає на швидкість. Скаляр\(a_{\text{N}}\) вимірює «скільки» прискорення перпендикулярно напрямку руху, тобто вимірює складову прискорення, що впливає на напрямок руху.

Ми можемо знайти,\(a_{\text{T}}\) використовуючи ортогональну проекцію\(\vecs a(t)\) onto\(\vecs T(t)\) (огляд Визначення 59 в розділі 10.3, якщо це необхідно).

Згадуючи, що так як\(\vecs T(t)\) є одиничним вектором\(\vecs T(t)\cdot\vecs T(t)=1\), тому ми маємо

\[\text{proj}_{T(t)}\vecs a(t) = \dfrac{\vecs a(t)\cdot\vecs T(t)}{\vecs T(t)\cdot\vecs T(t)}\vecs T(t) = \underbrace{\left(\vecs a(t)\cdot\vecs T(t)\right) }_{a_{\text{T}}}\vecs T(t).\]

Таким чином, сума\(\vecs a (t)\) в напрямку\(\vecs T(t)\) є\(a_{\text{T}}=\vecs a (t)\cdot\vecs T(t)\). Та ж логіка дає\(a_{\text{N}} = \vecs a (t)\cdot\vecs N(t)\).

Хоча це прекрасний спосіб обчислення\(a_{\text{T}}\), існують простіші способи пошуку\(a_{\text{N}}\) (оскільки пошук\(\vecs N\) себе може бути складним). Наступна теорема дає альтернативні формули для\(a_{\text{T}}\) і\(a_{\text{N}}\).

Примітка: Майте на увазі, що обидва\(a_\text{T}\) і\(a_\text{N}\) є функціями\(t\); тобто скалярні зміни в залежності від\(t\). Це умовність відкинути позначення\((t)\) ""\(a_\text{T}(t)\) і просто написати\(a_\text{T}\).

ТЕОРЕМА\(\PageIndex{2}\): Acceleration in the Plane Defined by \(\vecs T\) and \(\vecs N\)

\(\vecs r (t)\)Дозволяти позиційна функція з прискорення\(\vecs a (t)\) і одиниці тангенса і нормальних векторів\(\vecs T(t)\) і\(\vecs N(t)\). Потім\(\vecs a (t)\) лежить в площині,\(\vecs T(t)\) визначеній і\(\vecs N(t)\); тобто існують скаляри\(a_\text{T}\) і\(a_\text{N}\) такі, що

\[\vecs a (t) = a_\text{T}\vecs T(t) + a_\text{N}\vecs N(t).\]

Більш того,

\ [\ почати {вирівнювати*}
a_\ текст {T} &=\ векс a (t)\ cdot\ vecs T (t) =\ dfrac {d} {dt}\ лівий (\ норма {\ vecs v (t)}\ вправо)\\ [4pt]
a_\ текст {N} &=\ vecs a (t)\ cdot\ vecs N (t) =\ sqrt {\ норма {\ vecs a (t)} ^2-a_\ текст {T} ^2} =\ dfrac {\ norm {\ vecs a (t)\ times\ vecs v (t)}} {\ norm {\ vecs v (t)} =\ норма {\ vecs v (t)}\,\ норма {\ vecs T\, '(t)}
\ end {align*}\]

Зверніть увагу на другу формулу для\(a_\text{T}\):\( \dfrac{d}{dt}\left(\norm{\vecs v (t)}\right) \). Це вимірює швидкість зміни швидкості, яка знову-таки є величиною прискорення в напрямку руху.

Приклад\(\PageIndex{5}\): Computing \(a_\text{T}\) and \(a_\text{N}\)

Нехай\(\vecs r (t) = \langle 3\cos t, 3\sin t, 4t\rangle\) як у прикладах 11.4.1 і 11.4.3. Знайти\(a_\text{T}\) і\(a_\text{N}\).

Рішення

Попередні приклади наводимо\(\vecs a (t) = \langle -3\cos t,-3\sin t,0\rangle\) і

\[\vecs T(t) = \langle -\dfrac35\sin t,\dfrac35\cos t,\dfrac45\rangle \quad \text{and}\quad \vecs N(t) = \langle -\cos t,-\sin t,0\rangle.\]

Ми можемо знайти\(a_\text{T}\) та\(a_\text{N}\) безпосередньо з точковими продуктами:

\ [\ почати {вирівнювати*}
a_\ текст {T} &=\ векс а (т)\ cdot\ векс T (t) =\ dfrac95\ cos t\ dfrac95\ cos t\ sin t+0 = 0.\\ [4pt]
a_\ text {N} &=\ vecs a (t)\ cdot\ vecs N (t) = 3\ cos^2t+3\ sin^2t + 0 = 3.
\ end {вирівнювати*}\]

Таким чином\(\vecs a (t) = 0\vecs T(t) + 3\vecs N(t) = 3\vecs N(t)\), що явно так.

Яке практичне тлумачення цих чисел? \(a_\text{T}=0\)означає, що об'єкт рухається з постійною швидкістю, а значить, все прискорення відбувається у вигляді зміни напрямку.

Приклад\(\PageIndex{6}\): Computing \(a_\text{T}\) and \(a_\text{N}\)

Нехай\(\vecs r (t)=\langle t^2-t,t^2+t\rangle\) як в прикладах\(\PageIndex{2}\) і\(\PageIndex{4}\). Знайти\(a_\text{T}\) і\(a_\text{N}\).

Рішення

Попередні приклади наводимо\(\vecs a(t) = \langle 2,2\rangle\) і

\[\vecs T(t) = \langle \dfrac{2t-1}{\sqrt{8t^2+2}},\dfrac{2t+1}{\sqrt{8t^2+2}}\rangle \nonumber\]

і

\[ \vecs N(t) = \langle \dfrac{2t+1}{\sqrt{8t^2+2}},-\dfrac{2t-1}{\sqrt{8t^2+2}}\rangle. \nonumber\]

Хоча ми можемо обчислювати\(\vecs N(t)\),\(a_\text{N}\) використовуючи, ми замість цього демонструємо, використовуючи іншу формулу з теореми\(\PageIndex{2}\).

\ [\ почати {вирівнювати*}
a_\ текст {T} &=\ векс а (т)\ cdot\ векс T (t) =\ dfrac {4t-2} {\ sqrt {8t^2+2}} +\ dfrac {4t+2} {\ sqrt {8t^2+2}} =\ dfrac {8t} {\ sqrt {8t} ^2+2}}.\\ [4pt]
a_\ текст {N} &=\ sqrt {\ норма {\ vecs a (t)} ^2-a_\ текст {T} ^2} =\ sqrt {8-\ ліворуч (\ dfrac {8t} {8t^2+2}}\ праворуч) ^2} =\ dfrac {4} {квадратний {8 t^2+2}}
\ end {вирівнювати*}\]

Коли\(t=2\),\( a_\text{T} = \dfrac{16}{\sqrt{34}}\approx 2.74\) і\( a_\text{N} = \dfrac{4}{\sqrt{34}} \approx 0.69\). Ми інтерпретуємо це так, щоб означати\(t=2\), що частинка прискорюється здебільшого за рахунок збільшення швидкості, а не за рахунок зміни напрямку. Оскільки шлях поруч\(t=2\) є відносно прямим, це повинно мати інтуїтивний сенс. Рисунок\(\PageIndex{6}\) дає графік шляху для довідки.

Малюнок\(\PageIndex{6}\): Графік\(\vecs{r}(t)\) у прикладі\(\PageIndex{6}\).

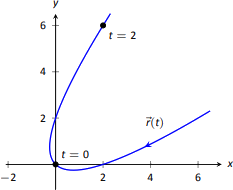
Контрастуйте це з\(t=0\) тим, де\(a_\text{T} = 0\) і\(a_\text{N} = 4/\sqrt{2}\approx 2.82\). Тут швидкість частинки не змінюється і все прискорення відбувається у вигляді зміни напрямку.

Приклад\(\PageIndex{7}\): Analyzing projectile motion

М'яч кидається з висоти 240ft з початковою швидкістю 64ft/s і кутом підйому\(30^\circ\). Знайдіть функцію\(\vecs r (t)\) положення м'яча і проаналізуйте\(a_\text{T}\) і\(a_\text{N}\).

Рішення

За допомогою Key Idea 53 розділу 11.3 формуємо позиційну функцію м'яча:

\[\vecs r (t) = \langle \left(64\cos 30^\circ\right) t, -16t^2+\left(64\sin 30^\circ\right) t+240\rangle,\]

які ми збудуємо на рис\(\PageIndex{7}\).

Малюнок\(\PageIndex{7}\): Побудова положення кинутого м'яча з кроком 1s показано.

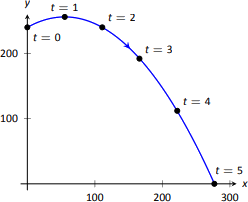
З цього знаходимо\(\vecs v (t) = \langle 64\cos 30^\circ, -32t+64\sin 30^\circ\rangle\) і\(\vecs a (t) = \langle 0,-32\rangle\). Обчислення не\(\vecs T(t)\) складно, і з деяким спрощенням ми знаходимо

\[\vecs T(t) = \langle \dfrac{\sqrt{3}}{\sqrt{t^2-2t+4}}, \dfrac{1-t}{\sqrt{t^2-2t+4}}\rangle.\]

З\(\vecs a (t)\) таким же простим, як це є, знайти\(a_\text{T}\) також просто:

\[a_\text{T} = \vecs a (t)\cdot \vecs T(t) = \dfrac{32t-32}{\sqrt{t^2-2t+4}}.\]

Вибираємо не знайти\(\vecs N(t)\) і знаходимо\(a_\text{N}\) через формулу\(a_\text{N} = \sqrt{\norm{\vecs a (t)}^2-a_\text{T}^2\,}\):

\[a_\text{N} = \sqrt{32^2-\left(\dfrac{32t-32}{\sqrt{t^2-2t+4}}\right)^2} = \dfrac{32\sqrt{3}}{\sqrt{t^2-2t+4}}.\]

На малюнку\(\PageIndex{8}\) наведено таблицю значень\(a_\text{T}\) і\(a_\text{N}\). Коли\(t=0\), ми бачимо, що швидкість м'яча зменшується; коли\(t=1\) швидкість м'яча незмінна. Це відповідає тому, що\(t=1\) на кулі досягає своєї найвищої точки.

Після\(t=1\) ми бачимо, що\(a_\text{N}\) зменшується в ціні. Це пов'язано з тим, що коли м'яч падає, його шлях стає прямішим, і більша частина прискорення відбувається у вигляді прискорення м'яча, а не в зміні його напрямку.

Малюнок\(\PageIndex{8}\): Таблиця значень\(a_T\) і\(a_N\) в прикладі\(\PageIndex{7}\).

Наше розуміння одиничного тангенса і нормальних векторів сприяє нашому розумінню руху. Робота в прикладі\(\PageIndex{7}\) дала кількісний аналіз того, що ми інтуїтивно знали.

Наступний розділ містить ще два важливі кроки на шляху до цього аналізу. Наразі ми описуємо позицію лише з точки зору часу. Однак у повсякденному житті ми часто описуємо положення з точки зору відстані («АЗС знаходиться приблизно на 2 милі попереду, зліва.»). Параметр довжини дуги дозволяє нам орієнтуватися на позицію з точки зору пройденої відстані.

Ми також інтуїтивно знаємо, що деякі шляхи пряміші за інші - а деякі «кривіші», ніж інші, але нам не вистачає вимірювання «кривизни». Параметр довжини дуги забезпечує нам спосіб обчислення кривизни, кількісного виміру того, наскільки крива крива.