13.3: Довжина дуги та кривизна

Last updated
Save as PDF

Page ID: 61639

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте довжину шляху частинки у просторі за допомогою функції довжини дуги.
Поясніть значення кривої кривої в просторі і викладіть її формулу.
Опишіть значення нормального та бінормального векторів кривої в просторі.

У цьому розділі ми вивчаємо формули, пов'язані з кривими як у двох, так і в трьох вимірах, і подивимося, як вони пов'язані з різними властивостями однієї і тієї ж кривої. Наприклад, припустимо, векторно-значна функція описує рух частинки в просторі. Ми хотіли б визначити, наскільки далеко пройшла частка за заданий проміжок часу, який можна описати довжиною дуги шляху, який вона слідує. Або, припустимо, що векторно-значна функція описує дорогу, яку ми будуємо, і ми хочемо визначити, наскільки різко криві дороги в даній точці. Це описується кривизною функції в цій точці. Ми досліджуємо кожне з цих понять в цьому розділі.

Довжина дуги для векторних функцій

Ми бачили, як векторна функція описує криву в двох або трьох вимірах. Нагадаємо, що формула довжини дуги кривої, визначеної параметричними функціями$x=x(t),y=y(t),t_1≤t≤t_2$, задається

\[s=\int^{t_2}_{t_1} \sqrt{(x′(t))^2+(y′(t))^2}dt. \nonumber \]

Аналогічним чином, якщо ми визначимо плавну криву за допомогою векторно-значної функції$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}$$a≤t≤b$, де довжина дуги задається формулою

\[s=\int^{b}_{a} \sqrt{(f′(t))^2+(g′(t))^2}dt. \nonumber \]

У трьох вимірах, якщо векторно-значна функція описується$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}$ через один і той же інтервал$a≤t≤b$, довжина дуги задається

\[s=\int^{b}_{a} \sqrt{(f′(t))^2+(g′(t))^2+(h′(t))^2}dt. \nonumber \]

Теорема: Формули довжини дуги для плоских і просторових кривих

Плоска крива: За умови гладкої кривої,$C$ визначеної функцією$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \, \hat{\mathbf{j}}$, де$t$ лежить в межах інтервалу$[a,b]$, довжина дуги$C$ над інтервалом дорівнює

\[\begin{align} s &=\int^{b}_{a} \sqrt{[f′(t)]^2+[g′(t)]^2}dt \\[4pt] &=\int^{b}_{a} \|\vecs r′(t)\|dt . \label{Arc2D}\end{align} \]

Космічна крива: За умови гладкої кривої$\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}$,$C$ визначеної функцією, де$t$ лежить в межах інтервалу$[a,b]$, довжина дуги$C$ над інтервалом дорівнює

\[\begin{align} s &=\int^{b}_{a} \sqrt{[f′(t)]^2+[g′(t)]^2+[h′(t)]^2}dt \\[4pt] &=\int^{b}_{a} \|\vecs r′(t)\|dt . \label{Arc3D} \end{align} \]

Дві формули дуже схожі, вони відрізняються лише тим, що просторова крива має три компонентні функції замість двох. Зауважте, що формули визначені для гладких кривих: кривих, де векторно-значна функція$\vecs r(t)$ диференційовна з ненульовою похідною. Умова гладкості гарантує, що крива не має згинів (або кутів), які могли б зробити формулу проблематичною.

Приклад$\PageIndex{1}$: Finding the Arc Length

Обчисліть довжину дуги для кожної з наступних векторних функцій:

$\vecs r(t)=(3t−2) \,\hat{\mathbf{i}}+(4t+5) \,\hat{\mathbf{j}},\quad 1≤t≤5$
$\vecs r(t)=⟨t\cos t,t\sin t,2t⟩,0≤t≤2 \pi $

Рішення

Використання рівняння\ ref {Arc2D}$\vecs r′(t)=3 \,\hat{\mathbf{i}}+4 \,\hat{\mathbf{j}}$, так
\[\begin{align*} s &=\int^{b}_{a} \|\vecs r′(t)\|dt \\[4pt] &=\int^{5}_{1} \sqrt{3^2 + 4^2} dt \\[4pt] &=\int^{5}_{1} 5 dt = 5t\big|^{5}_{1} = 20. \end{align*}\]
Використання рівняння\ ref {Arc3D}$\vecs r′(t)=⟨ \cos t−t \sin t, \sin t+t \cos t,2⟩ $, так
\[\begin{align*} s &=\int^{b}_{a} ∥\vecs r′(t)∥dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{(\cos t−t \sin t)^2+( \sin t+t \cos t)^2+2^2} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{( \cos ^2 t−2t \sin t \cos t+t^2 \sin ^2 t)+( \sin^2 t+2t \sin t \cos t+t^2 \cos ^2 t)+4} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{\cos ^2 t+ \sin^2 t+t^2( \cos ^2 t+ \sin ^2 t)+4} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{t^2+5} dt\end{align*}\]

Тут ми можемо використовувати формулу інтеграції таблиці

\[\int \sqrt{u^2+a^2}du = \dfrac{u}{2}\sqrt{u^2+a^2} + \dfrac{a^2}{2} \ln \,\left|\, u + \sqrt{u^2+a^2} \,\right| + C, \nonumber \]

таким чином отримуємо

\[\begin{align*} \int^{2 \pi}_{0} \sqrt{t^2+5} dt \; &= \frac{1}{2} \bigg( t \sqrt{t^2+5}+5 \ln \,\left|t+\sqrt{t^2+5}\right| \bigg) _0^{2π} \\[4pt] &= \frac{1}{2} \bigg( 2π \sqrt{4π^2+5}+5 \ln \bigg( 2π+ \sqrt{4π^2+5} \bigg) \bigg)−\frac{5}{2} \ln \sqrt{5} \\[4pt] &≈25.343 \,\text{units}. \end{align*}\]

Вправа$\PageIndex{1}$

Обчислити довжину дуги параметризованої кривої

\[\vecs r(t)=⟨2t^2+1,2t^2−1,t^3⟩,\quad 0≤t≤3. \nonumber \]

Підказка: Використовуйте рівняння\ ref {Arc3D}.
Відповідь: $\vecs r′(t)=⟨4t,4t,3t^2⟩,$так$s= \frac{1}{27}(113^{3/2}−32^{3/2})≈37.785$ одиниць

Тепер ми повернемося до спіралі, введеної раніше в цьому розділі. Векторно-значну функцію, що описує спіраль, можна записати у вигляді

\[\vecs r(t)=R \cos \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}} +R \sin \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}},0≤t≤h, \nonumber \]

де$R$ представляє радіус спіралі,$h$ представляє висоту (відстань між двома послідовними витками), а спіраль завершує$N$ повороти. Виведемо формулу довжини дуги цієї спіралі за допомогою Equation\ ref {Arc3D}. Перш за все,

\[\vecs r′(t)=−\dfrac{2πNR}{h} \sin \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}}+ \dfrac{2πNR}{h} \cos \left(\dfrac{2πNt}{h} \right) \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}. \nonumber \]

Тому,

\[\begin{align*} s & =\int_a^b ‖\vecs r′(t)‖dt \\[4pt] &=\int_0^h\sqrt{ \bigg(−\dfrac{2πNR}{h} \sin \bigg(\dfrac{2πNt}{h} \bigg) \bigg)^2+ \bigg( \dfrac{2πNR}{h} \cos \bigg( \dfrac{2πNt}{h} \bigg) \bigg)^2+1^2}dt \\[4pt] &=\int_0^h\sqrt{ \dfrac{4π^2N^2R^2}{h^2} \bigg( \sin ^2 \bigg(\dfrac{2πNt}{h} \bigg) + \cos ^2 \bigg( \dfrac{2πNt}{h} \bigg) \bigg)+1}dt \\[4pt] &=\int_0^h\sqrt{ \dfrac{4π^2N^2R^2}{h^2} +1}dt \\[4pt] &=\bigg[ t\sqrt{ \dfrac{4π^2N^2R^2}{h^2} +1}\bigg]^h_0 \\[4pt] &=h \sqrt{ \dfrac{4π^2N^2R^2 + h^2}{h^2}} \\[4pt] &=\sqrt{ 4π^2N^2R^2 + h^2}.\end{align*}\]

Це дає формулу довжини дроту, необхідної для формування спіралі з$N$ витками, яка має радіус$R$ і висоту$h$.

Параметризація довжини дуги

Тепер у нас є формула довжини дуги кривої, визначеної векторною функцією. Давайте зробимо цей крок далі і розглянемо, що таке функція довжини дуги.

Якщо векторно-значна функція представляє положення частинки в просторі як функцію часу, то функція довжини дуги вимірює, наскільки далеко ця частинка рухається як функція часу. Формула функції довжини дуги випливає безпосередньо з формули довжини дуги:

\[s=\int^{t}_{a} \sqrt{(f′(u))^2+(g′(u))^2+(h′(u))^2}du. \label{arclength2} \]

Якщо крива знаходиться в двох вимірах, то під квадратним коренем всередині інтеграла з'являються тільки два члени. Причина використання незалежної змінної u полягає в тому, щоб розрізняти час і змінну інтеграції. Оскільки$s(t)$ вимірює пройдену відстань як функція часу,$s′(t)$ вимірює швидкість частинки в будь-який момент часу. Оскільки у нас є формула для$s(t)$ в Equation\ ref {arclength2}, ми можемо диференціювати обидві сторони рівняння:

\[ \begin{align*} s′(t) &=\dfrac{d}{dt} \bigg[ \int^{t}_{a} \sqrt{(f′(u))^2+(g′(u))^2+(h′(u))^2}du \bigg] \\[4pt] &=\dfrac{d}{dt} \bigg[ \int^{t}_{a} ‖\vecs r′(u)‖du \bigg] \\[4pt] &=\|\vecs r′(t)\|.\end{align*}\]

Якщо припустити, що$\vecs r(t)$ визначає плавну криву, то довжина дуги завжди збільшується, так$s′(t)>0$ для$t>a$. Останній,$\vecs r(t)$ якщо крива по якій$\|\vecs r′(t)\|=1 $ для всіх$t$, то

\[s(t)=\int^{t}_{a} ‖\vecs r′(u)‖\,du=\int^{t}_{a} 1\,du=t−a, \nonumber \]

що означає, що$t$ представляє довжину дуги до тих пір, поки$a=0$.

Теорема: Функція довжини дуги

$\vecs r(t)$Опишемо плавну криву для$t≥a$. Тоді функція довжини дуги задається

\[s(t)=\int^{t}_{a} ‖\vecs r′(u)‖\,du \nonumber \]

Крім того,

\[\dfrac{ds}{dt}=‖\vecs r′(t)‖>0. \nonumber \]

Якщо$‖\vecs r′(t)‖=1$ для всіх$t≥a$, то параметр$t$ представляє довжину дуги від початкової точки в$t=a$.

Корисним застосуванням цієї теореми є пошук альтернативної параметризації заданої кривої, яка називається параметризацією довжини дуги. Нагадаємо, що будь-яка векторно-значна функція може бути перепараметризована за допомогою зміни змінних. Наприклад, якщо у нас є функція,$\vecs r(t)=⟨3 \cos t,3 \sin t⟩,0≤t≤2π$ яка параметризує коло радіуса 3, ми можемо змінити параметр від$t$ до$4t$, отримавши нову параметризацію$\vecs r(t)=⟨3 \cos 4t,3 \sin 4t⟩$. Нова параметризація все ще визначає коло радіуса 3, але тепер нам потрібно використовувати лише значення,$0≤t≤π/2$ щоб пройти коло один раз.

Припустимо, що ми знаходимо функцію довжини дуги$s(t)$ і можемо вирішити цю функцію для$t$ як функції$s$. Потім ми можемо перепараметризувати вихідну функцію,$\vecs r(t)$ підставляючи вираз для$t$ назад в$\vecs r(t)$. Векторно-значна функція тепер записується через параметр$s$. Оскільки змінна$s$ представляє довжину дуги, ми називаємо це параметризацією довжини дуги вихідної функції$\vecs r(t)$. Однією з переваг знаходження параметризації довжини дуги є те, що відстань, пройдена по кривій, починаючи з, тепер$s=0$ дорівнює параметру$s$. Параметризація довжини дуги також з'являється в контексті кривизни (яку ми розглянемо далі в цьому розділі) та лінійних інтегралів.

Приклад$\PageIndex{2}$: Finding an Arc-Length Parameterization

Знайдіть параметризацію довжини дуги для кожної з наступних кривих:

$\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+ 4 \sin t \,\hat{\mathbf{j}},\quad t≥0$
$\vecs r(t)=⟨t+3,2t−4,2t⟩,\quad t≥3$

Рішення

Спочатку знайдемо функцію довжини дуги за допомогою Equation\ ref {arclength2}:
\[\begin{align*} s(t) &= \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_0^t ‖⟨−4 \sin u,4 \cos u⟩‖ \,du \\[4pt] &= \int_0^t \sqrt{(−4 \sin u)^2+(4 \cos u)^2} \,du \\[4pt] &= \int_0^t \sqrt{16 \sin ^2 u+16 \cos ^2 u} \,du \\[4pt] &= \int_0^t 4\,du = 4t, \end{align*}\]
що дає залежність між довжиною дуги$s$ і параметром$t$ як$s=4t;$ так,$t=s/4$. Далі замінюємо змінну$t$ в оригінальній функції$\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}$ виразом$s/4$ для отримання
\[\vecs r(s)=4 \cos \left(\frac{s}{4}\right) \,\hat{\mathbf{i}} + 4 \sin \left( \frac{s}{4}\right) \,\hat{\mathbf{j}}. \nonumber \]
Це і є параметризація довжини дуги$\vecs r(t)$. Оскільки початкове обмеження на$t$ було надано$t≥0$, обмеження на s стає$s/4≥0$, або$s≥0$.
Функція довжини дуги задається рівнянням\ ref {arclength2}:
\[\begin{align*} s(t) & = \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_3^t ‖⟨1,2,2⟩‖ \,du \\[4pt] &= \int_3^t \sqrt{1^2+2^2+2^2} \,du \\[4pt] &= \int_3^t 3 \,du \\[4pt] &= 3t - 9. \end{align*}\]
Тому залежність між довжиною дуги$s$ і параметром$t$ є$s=3t−9$, так$t= \frac{s}{3}+3$. Підстановка this у вихідну функцію$\vecs r(t)=⟨t+3,2t−4,2t⟩ $ дає
\[\vecs r(s)=⟨\left(\frac{s}{3}+3\right)+3,\,2\left(\frac{s}{3}+3\right)−4,\,2\left(\frac{s}{3}+3\right)⟩=⟨\frac{s}{3}+6, \frac{2s}{3}+2,\frac{2s}{3}+6⟩.\nonumber \]
Це параметризація довжини дуги$\vecs r(t)$. Первісне обмеження по параметру$t$ було$t≥3$, тому обмеження на$s$ є$(s/3)+3≥3$, або$s≥0$.

Вправа$\PageIndex{2}$

Знайти функцію довжини дуги для спіралі

\[\vecs r(t)=⟨3 \cos t, 3 \sin t,4t⟩,\quad t≥0. \nonumber \]

Потім використовуйте зв'язок між довжиною дуги та параметром,$t$ щоб знайти параметризацію довжини дуги$\vecs r(t)$.

Підказка

Почніть з пошуку функції довжини дуги.

Відповідь

$s=5t$, або$t=s/5$. Підставляючи це на$\vecs r(t)=⟨3 \cos t,3 \sin t,4t⟩$ дає

\[\vecs r(s)=⟨3 \cos \left(\frac{s}{5}\right),3 \sin \left(\frac{s}{5}\right),\frac{4s}{5}⟩,\quad s≥0 \nonumber \]

викривлення

Важливою темою, пов'язаною з довжиною дуги, є кривизна. Поняття кривизни передбачає спосіб вимірювання того, наскільки різко крутиться плавна крива. Коло має постійну кривизну. Чим менше радіус кола, тим більше кривизна.

Подумайте про те, щоб їхати по дорозі. Припустимо, дорога лежить на дузі великого кола. В цьому випадку вам ледве доведеться крутити колесо, щоб залишитися на дорозі. Тепер припустимо, радіус менше. В цьому випадку потрібно буде поворот різкіше, щоб залишитися на дорозі. У випадку кривої, відмінної від кола, часто корисно спочатку вписати коло до кривої в заданій точці, щоб вона була дотичною до кривої в цій точці і «обіймав» криву якомога ближче в районі точки (рис.$\PageIndex{1}$). Викривлення графіка в цій точці визначається таким же, як і кривизна вписаного кола.

Ця цифра є графіком кривої. Крива піднімається і падає в першому квадранті. Уздовж кривої, де крива змінюється від спадної до зростаючої, йде коло. Нижня частина кола крива така ж, як і графік кривої. Існує також друге менше коло, де крива переходить від збільшення до зменшення. Частина кола припадає на криву. Обидва кола мають представлений радіус r. — Малюнок$\PageIndex{1}$: Графік представляє кривизну функції$y=f(x).$ Чим гостріше поворот на графіку, тим більша кривизна і менший радіус вписаного кола.

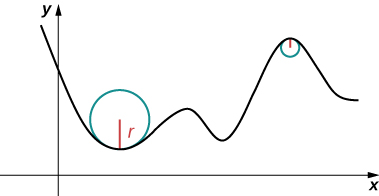
Визначення: Кривизна

$C$Дозволяти плавна крива в площині або в просторі$\vecs r(s)$, заданому, де$s$ параметр довжини дуги. Викривлення$κ$ при$s$ є

\[κ =\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}=‖\vecs T′(s)‖. \nonumber \]

Відвідайте це відео для отримання додаткової інформації про кривизну космічної кривої.

Формула при визначенні кривизни не дуже корисна в плані розрахунку. Зокрема, нагадаємо, що$\vecs T(t)$ являє собою одиничний дотичний вектор до заданої векторно-значної функції$\vecs r(t)$, а$\vecs T(t)$ формула для

\[\vecs T(t)=\frac{\vecs r′(t)}{∥\vecs r′(t)∥}. \nonumber \]

Щоб скористатися формулою кривизни, спочатку потрібно$\vecs r(t)$ висловити через параметр довжини дуги$s$, потім знайти одиничний$\vecs T(s)$ тангенс вектора$\vecs T(s)$ для функції$\vecs r(s)$, потім взяти похідну по відношенню до$s$. Це виснажливий процес. На щастя, існують еквівалентні формули для кривизни.

Теорема: Альтернативні формули кривизни

Якщо$C$ це плавна крива$\vecs r(t)$, задана, то$κ$$C$ кривизна at$t$ задається

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}. \label{EqK2} \]

Якщо$C$ тривимірна крива, то кривизну можна задати за формулою

\[κ =\dfrac{‖\vecs r′(t)×\vecs r′′(t)‖}{‖\vecs r′(t)‖^3}.\label{EqK3} \]

Якщо$C$ графік функції$y=f(x)$ і обидві$y′$ і$y''$ існують, то$κ$ кривизна в точці$(x,y)$ задається

\[κ =\dfrac{|y''|}{[1+(y′)^2]^{3/2}}.\label{EqK4} \]

Доказ

Перша формула випливає безпосередньо з правила ланцюга:

\[\dfrac{d\vecs{T}}{dt} = \dfrac{d\vecs{T}}{ds} \dfrac{ds}{dt}, \nonumber \]

де$s$ - довжина дуги по кривій$C$. Розділення обох сторін на$ds/dt$, і прийняття величини обох сторін дає

\[\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}= \left\lVert\frac{\vecs T′(t)}{\dfrac{ds}{dt}}\right\rVert.\nonumber \]

Так як$ds/dt=‖\vecs r′(t)‖$, це дає формулу кривизни$κ$ кривої з$C$ точки зору будь-якої параметризації$C$:

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}.\nonumber \]

У випадку з тривимірною кривою починаємо з формул$\vecs T(t)=(\vecs r′(t))/‖\vecs r′(t)‖$ і$ds/dt=‖\vecs r′(t)‖$. Тому,$\vecs r′(t)=(ds/dt)\vecs T(t)$. Ми можемо взяти похідну від цієї функції за допомогою скалярної формули добутку:

\[\vecs r″(t)=\dfrac{d^2s}{dt^2}\vecs T(t)+\dfrac{ds}{dt}\vecs T′(t).\nonumber \]

Використовуючи ці останні два рівняння, отримаємо

\[\begin{align*} \vecs r′(t)×\vecs r″(t) &=\dfrac{ds}{dt}\vecs T(t)× \bigg( \dfrac{d^2s}{dt^2}\vecs T(t)+\dfrac{ds}{dt}\vecs T′(t) \bigg) \\[4pt] &=\dfrac{ds}{dt} \dfrac{d^2s}{dt^2}\vecs T(t)×\vecs T(t)+(\dfrac{ds}{dt})^2\vecs T(t)×\vecs T′(t). \end{align*}\]

Так як$\vecs T(t)×\vecs T(t)=0$, це зводиться до

\[\vecs r′(t)×\vecs r′′(t)=\left(\dfrac{ds}{dt}\right)^2\vecs T(t)×\vecs T′(t).\nonumber \]

Оскільки паралельно і$\vecs T′$$\vecs T$ є ортогональним до$\vecs N$, то випливає, що$\vecs T$ і$\vecs T′$ є ортогональними.$\vecs N$ Це означає, що$‖\vecs T×\vecs T′‖=‖\vecs T‖‖\vecs T′‖ \sin (π/2)=‖\vecs T′‖$,

\[\|\vecs r′(t)×\vecs r″(t)\|=\left(\dfrac{ds}{dt}\right)^2‖\vecs T′(t)‖.\nonumber \]

Тепер вирішимо це рівняння для$‖\vecs T′(t)‖$ і використовуємо той факт, що$ds/dt=‖\vecs r′(t)‖$:

\[‖\vecs T′(t)‖=\dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^2}.\nonumber \]

Потім, ділимо обидві сторони на$‖\vecs r′(t)‖$. Це дає

\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}=\dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3}.\nonumber \]

Це доводить$\ref{EqK3}$. Щоб довести$\ref{EqK4}$, почнемо з припущення, що крива$C$ визначається функцією$y=f(x)$. Тоді ми можемо визначити$\vecs r(t)=x \,\hat{\mathbf{i}}+f(x) \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$. Використання попередньої формули для кривизни:

\[\begin{align*} \vecs r′(t) &=\,\hat{\mathbf{i}}+f′(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r″(t) &=f″(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r′(t)×\vecs r″(t) &= \begin{vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 1 & f′(x) & 0 \\ 0 & f″(x) & 0 \end{vmatrix} =f″(x)\,\hat{\mathbf{k}}. \end{align*}\]

Тому,

\[κ= \dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3}=\dfrac{|f″(x)|}{(1+[f′(x)]^2)^{3/2}} \nonumber \]

Приклад$\PageIndex{3}$: Finding Curvature

Знайдіть кривизну для кожної з наступних кривих у заданій точці:

$\vecs r(t)=4 \cos t\,\hat{\mathbf{i}}+4 \sin t\,\hat{\mathbf{j}}+3t\,\hat{\mathbf{k}},\quad t=\dfrac{4π}{3}$
$\mathrm{f(x)= \sqrt{4x−x^2},x=2}$

Рішення

Ця функція описує спіраль.

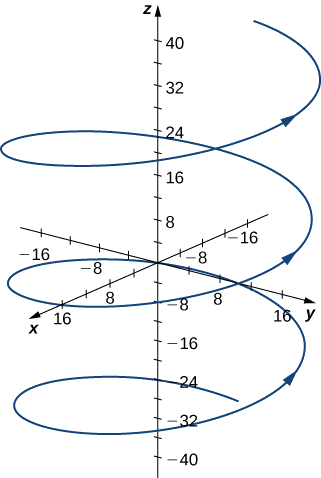
$Ця цифра є графіком кривої в 3-х вимірах. Крива являє собою спіраль, яка спіралі навколо осі z. Він починається нижче площини xy і спіралі вгору з орієнтацією.$

Викривлення спіралі при$t=(4π)/3$ можна дізнатися за допомогою$\ref{EqK2}$. Спочатку розрахуйте$\vecs T(t)$:

\[\begin{align*} \vecs T(t) &=\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖} \\[4pt] &=\dfrac{⟨−4 \sin t,4 \cos t,3⟩}{\sqrt{(−4 \sin t)^2+(4 \cos t)^2+3^2}}\\[4pt] &=⟨−\dfrac{4}{5} \sin t,\dfrac{4}{5} \cos t, \dfrac{3}{5}⟩. \end{align*}\]

Далі розрахуйте$\vecs T′(t):$

\[\vecs T′(t)=⟨−\dfrac{4}{5} \cos t,− \dfrac{4}{5} \sin t,0⟩. \nonumber \]

Останній, застосовуйте$\ref{EqK2}$:

\[ \begin{align*} κ &=\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖} = \dfrac{‖⟨−\dfrac{4}{5} \cos t,−\dfrac{4}{5} \sin t,0⟩‖}{‖⟨−4 \sin t,4 \cos t,3⟩‖} \\[4pt] &=\dfrac{\sqrt{(−\dfrac{4}{5} \cos t)^2+(−\dfrac{4}{5} \sin t)^2+0^2}}{\sqrt{(−4 \sin t)^2+(4 \cos t)^2+ 3^2}} \\[4pt] &=\dfrac{4/5}{5}=\dfrac{4}{25}. \end{align*}\]

Кривизна цієї спіралі постійна у всіх точках спіралі.

Ця функція описує півколо.

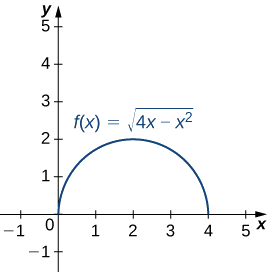
$Ця цифра є графіком півкола. Він знаходиться в першому квадранті. Півколо починається біля початку і зупиняється на 4 на осі х. Півколо представляє функцію f (x) = квадратний корінь (4x-x^2).$

Щоб знайти кривизну цього графіка, ми повинні використовувати$\ref{EqK4}$. Для початку розраховуємо$y′$ і$y″:$

\[\begin{align*}y &=\sqrt{4x−x^2}=(4x−x^2)^{1/2} \\[4pt] y′ &=\dfrac{1}{2}(4x−x^2)^{−1/2}(4−2x)=(2−x)(4x−x^2)^{−1/2} \\[4pt] y″ &=−(4x−x^2)^{−1/2}+(2−x)(−\dfrac{1}{2})(4x−x^2)^{−3/2}(4−2x) \\[4pt] & =−\dfrac{4x−x^2}{(4x−x^2)^{3/2}}− \dfrac{(2−x)^2}{(4x−x^2)^{3/2}} \\[4pt] &=\dfrac{x^2−4x−(4−4x+x^2)}{(4x−x^2)^{3/2}} \\[4pt] &=−\dfrac{4}{(4x−x^2)^{3/2}}. \end{align*} \nonumber \]

Потім застосовуємо$\ref{EqK4}$:

\[ \begin{align*} κ &=\dfrac{|y''|}{[1+(y′)^2]^{3/2}} \\[4pt] &= \dfrac{\bigg| −\dfrac{4}{(4x−x^2)^{3/2}}\bigg|}{\bigg[1+((2−x)(4x−x^2)^{−1/2})^2 \bigg]^{3/2}} = \dfrac{\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg|}{\bigg[ 1+\dfrac{(2−x)^2}{4x−x^2} \bigg]^ {3/2}} \\[4pt] &= \dfrac{\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg|}{ \bigg[ \dfrac{4x−x^2+x^2−4x+4}{4x−x^2} \bigg]^{3/2}}=\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg| ⋅\dfrac{(4x−x^2)^{3/2}}{8} \\[4pt] &=\dfrac{1}{2}. \end{align*}\]

Кривизна цього кола дорівнює зворотній його радіусу. Існує незначна проблема з абсолютним значенням в$\ref{EqK4}$; однак, уважний погляд на розрахунок показує, що знаменник є позитивним для будь-якого значення$x$.

Вправа$\PageIndex{3}$

Знайти кривизну кривої, визначеної функцією

\[y=3x^2−2x+4 \nonumber \]

в точці$x=2$.

Підказка: Використовувати$\ref{EqK4}$.
Відповідь: $κ \; =\frac{6}{101^{3/2}}≈0.0059$

Нормальний і бінормальний вектори

Ми бачили, що похідна$\vecs r′(t)$ векторно-значної функції є дотичним вектором до кривої$\vecs r(t)$, визначеної, і одиничний тангенс вектор$\vecs T(t)$ можна обчислити$\vecs r′(t)$ діленням на її величину. При вивченні руху в трьох вимірах для опису руху частинки по шляху в просторі корисні два інших вектора: основний одиничний вектор нормалі і бінормальний вектор.

Визначення: Бінормальні вектори

$C$Дозволяти тривимірна плавна крива представлена$\vecs r$ через відкритий інтервал$I$. Якщо$\vecs T′(t)≠\vecs 0$, то основна одиниця нормального вектора$t$ при визначена бути

\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \label{EqNormal} \]

Бінормальний вектор at$t$ визначається як

\[\vecs B(t)=\vecs T(t)×\vecs N(t),\label{EqBinormal} \]

де$\vecs T(t)$ - одиничний тангенс вектора.

Зауважимо, що за визначенням бінормальний вектор ортогональний як до одиничного дотичного вектора, так і вектору нормалі. Крім того, завжди$\vecs B(t)$ є одиничним вектором. Це можна показати за допомогою формули величини перехресного добутку.

\[‖\vecs B(t)‖=‖\vecs T(t)×\vecs N(t)‖=‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta, \nonumber \]

де$\theta$ - кут між$\vecs T(t)$ і$\vecs N(t)$. Оскільки$\vecs N(t)$ є похідною одиничного вектора, властивість (vii) похідної векторно-значної функції говорить нам про те, що$\vecs T(t)$ і$\vecs N(t)$ є ортогональними один до одного, так$\theta=π/2$. Крім того, вони обидва є одиничними векторами, тому їх величина дорівнює 1. Тому$‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta=(1)(1) \sin (π/2)=1$ і$\vecs B(t)$ є одиничним вектором.

Основний вектор нормальної одиниці може бути складним для обчислення, оскільки дотичний вектор одиниці включає частку, і цей частка часто має квадратний корінь у знаменнику. У тривимірному випадку знаходження перехресного добутку одиничного дотичного вектора і одиничного нормального вектора може бути ще більш громіздким. На щастя, у нас є альтернативні формули для пошуку цих двох векторів, і вони представлені в Motion in Space.

Приклад$\PageIndex{4}$: Finding the Principal Unit Normal Vector and Binormal Vector

Для кожної з наступних векторно-значних функцій знайдіть основний одиничний нормальний вектор. Потім, якщо можливо, знайдіть бінормальний вектор.

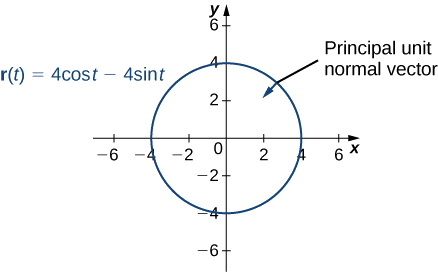
$\vecs r(t)=4 \cos t\,\hat{\mathbf{i}}− 4 \sin t\,\hat{\mathbf{j}}$
$\vecs r(t)=(6t+2)\,\hat{\mathbf{i}}+5t^2\,\hat{\mathbf{j}}−8t\,\hat{\mathbf{k}}$

Рішення

Ця функція описує коло.

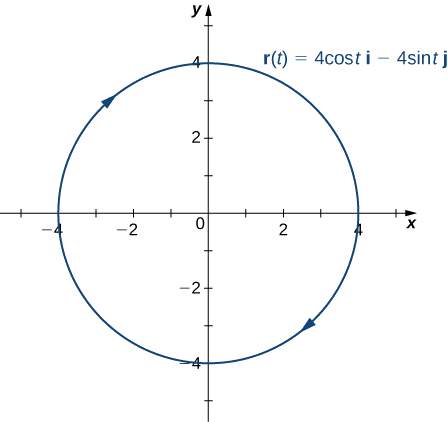
$Ця цифра є графіком окружності з центром у початку координат з радіусом 2. Орієнтація кола - за годинниковою стрілкою. Він являє собою векторну функцію r (t) = 4costi — 4 sintj.$

Щоб знайти основний блок нормального вектора, ми спочатку повинні знайти одиничний тангенс вектора$\vecs T(t):$

\ [\ почати {вирівнювати*}\ векс T (t) &=\ dfrac {\ vecs r′ (t)} {\ векс r′ (t) ⟩}\\ [4pt]
&=\ dfrac {−4\ sin t\,\ hat {\ mathbf {i}} −4\ cos t\,\ hat {\ mathbf {j}} {\ sqrt {(−4\ sin t) ^2+ (−4\ cos t) ^2}}\\ [4pt]
&=\ dfrac {−4\ sin t\,\ hat {\ mathbf {i}} −4\ cos t\,\ hat {\ mathbf {j}}} {\ sqrt {16\ sin ^2 t+16\ cos ^2 t}}\\ [4pt]
&=\ dfrac {−4\ sin t\,\ hat {\ mathbf {i}} −4\ cos t\,\ hat {\ mathbf {j}} {\ sqrt {16 (\ sin ^2 t+\ cos ^2 t)}}\ [4pt]
&=\ dfrac {−4\ sin t\,\ hat {\ mathbf {i}} −4\ cos t\,\ hat {\ mathbf {j}} {4}\\[4pt] &=− \sin t\,\hat{\mathbf{i}}− \cos t\,\hat{\mathbf{j}}.\end{align*}\]

Далі використовуємо$\ref{EqNormal}$:

\ [\ почати {вирівнювати*}\ векс N (t) &=\ dfrac {\ vecs T′ (t)} {\ vecs T′ (t) ⟩}\\ [4pt] &=\ dfrac {-\ cos t\,\ hat {\ mathbf {\ mathbf {i}} +\ sin t\,\ hat {\ mathbf {j}}\ sqrt {(−\ cos t) ^2+ (\ sin t) ^2}}\\ [4pt]
&=\ dfrac {−\ cos t\,\ hat {\ mathbf {i}} +\ sin t\,\ hat {\ mathbf {j}} {\ sqrt {\ cos ^2 t+\ sin ^2 t}}\\ 4 пт]
&=−\ cos t\,\ hat {\ mathbf {i}} +\ sin t\,\ hat {\ mathbf {j}}. \ end {вирівнювати*}\]

Зверніть увагу, що одиничний тангенс вектор і основний одиничний нормальний вектор ортогональні один до одного для всіх значень$t$:

\[\begin{align*} \vecs T(t)·\vecs N(t) &=⟨− \sin t,− \cos t⟩·⟨− \cos t, \sin t⟩ \\[4pt] &= \sin t \cos t−\cos t \sin t \\[4pt] &=0. \end{align*}\]

Крім того, основна одиниця нормального вектора вказує на центр кола від кожної точки кола. Оскільки$\vecs r(t)$ визначає криву в двох вимірах, ми не можемо обчислити бінормальний вектор.

$Ця цифра є графіком окружності з центром у початку координат з радіусом 2. Орієнтація кола - за годинниковою стрілкою. Він являє собою векторну функцію r (t) = 4costi — 4 sintj. На колі в першому квадранті знаходиться вектор, спрямований всередину. Він позначений як «основний блок нормального вектора».$

Виглядає ця функція наступним чином:

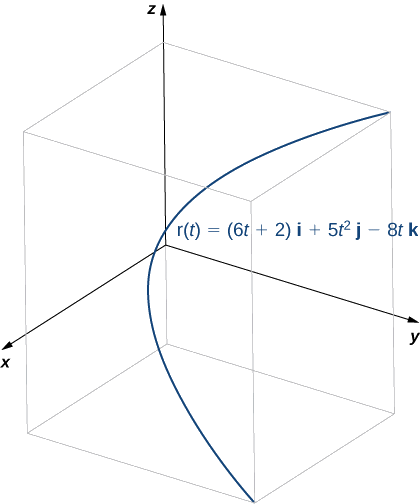
$Ця цифра являє собою криву в 3 вимірах. Він знаходиться всередині коробки. Коробка являє собою перший октант. Крива починається в правому нижньому куті поля і крива через поле в параболічній кривій вгорі.$

Щоб знайти основний блок нормального вектора, спочатку знайдемо одиничний тангенс вектора$\vecs T(t):$

\ [\ почати {вирівнювати*}\ векс T (t) &=\ dfrac {\ vecs r′ (t)} {\ векс r′ (t) ⟩}\\ [4pt]
&=\ dfrac {6\,\ капелюх {\ mathbf {i}} +10t\,\ капелюх {\ mathbf {j}} −8\,\ капелюх {\ {\ mathbf {k}}} {\ sqrt {6^2+ (10t) ^2+ (−8) ^2}}\\ [4pt]
&=\ dfrac {6\,\ капелюх {\ mathbf {i}} +10t\,\ капелюх {\ mathbf {j}} −8\,\ капелюх {\ mathbf {k}}} {\ sqrt {36+100t^2+64 }}\\ [4pt]
&=\ dfrac {6\,\ капелюх {\ mathbf {я}} +10т\,\ капелюх {\ mathbf {j}} −8\,\ капелюх {\ mathbf {k}} {\ sqrt {100 (t^2+1)}}\\ [4pt]
&=\ dfrac {3\\\ капелюх {\ mathbf {i}} −5т\,\ капелюх {\ mathbf {j}} −4\,\ капелюх {\ mathbf {k}}} {5\ sqrt {t^2+1}}\\ [4pt]
&=\ dfrac {3} {5} (t^2+1) ^ {−1/2}\,\ капелюх {\ max thbf {i}} −t (t^2 +1) ^ {−1/2}\,\ hat {\ mathbf {j}} −\ dfrac {4} {5} (t^2+1) ^ {−1/2}\,\ hat {\ mathbf {k}}. \ end {вирівнювати*}\]

Далі розраховуємо$\vecs T′(t)$ і$‖\vecs T′(t)‖$:

\ [\ почати {вирівнювати*}\ векс T′ (t) &=\ dfrac {3} {5} (−\ dfrac {1} {2}) (t^2+1) ^ {−3/2} (2t)\,\ hat {\ mathbf {i}} − ((t^2+1) ^ {1/2} −t (\ dfrac {1} {2}) (t^2+1) ^ {−3/2} (2t))\,\ капелюх {\ mathbf {j}}} −\ dfrac {4} {5} (−\ dfrac {1} {2}) (t^2+1) ^ {−3/2} (2t)\,\ капелюх {\ mathbf {k}}\\ 4pt]
&=−\ dfrac {3t} {5 (t^2+1) ^ {3/2}}\,\ hat {\ mathbf {i}} −\ dfrac { 1} {(t^2+1) ^ {3/2}}\,\ hat {\ mathbf {j}} +\ dfrac {4t} {5 (t^2+1) ^ {3/2}}\,\ капелюх {\ mathbf {k}}\\ [4pt] dfrac {3t} {5 (t^2+1) ^ {3/2}}\ великий) ^2+\ великий (−\ dfrac {1} {(t^2+1) ^ {3/2}}\ великий) ^2+\ bigg (\ dfrac {4t} {5 (t^2+1) ^ {3/2}}\ bigg) ^2} ^2} ^2} ^2}\ [4pt]
&=\ sqrt {\ dfrac {9t^2} {25 (t^2+1) ^3} +\ dfrac {1} {(t^2+1) ^3} +\ dfrac {16t^2} {25 (t^2+1) ^3}}\\ [4pt]
&=\ sqrt {\ dfrac {25t^2+25} {25 (t^2+1) ^3}}\\ [4pt]
&=\ sqrt {\ dfrac {1} {(t^2+1) ^2}}\\ [4pt]
&=\ dfrac {1} {t^2+1}. \ end {вирівнювати*}\]

Тому, згідно з$\ref{EqNormal}$:

\ [\ почати {вирівнювати*}\ векс N (t) &=\ dfrac {\ vecs T′ (t)} {\ векс T′ (t) ⟩}\\ [4pt]
&=\ bigg (−\ dfrac {3t} {5 (t^2+1) ^ {3/2}}\,\ hat {\ mathbf {i}}\ dfrac {1} {(t^2+1) ^ {3/2}}\,\ капелюх {\ mathbf {j}} +\ dfrac {4t} {5 (t^2+1) ^ {3/2}}\ капелюх {\ mathbf {k}}\ bigg) (t^2+1)\\ [4pt]
&= −\ dfrac {3t} {5 (t^2+1) ^ {1/2}}\,\ капелюх {\ mathbf {i}} −\ dfrac {5} {5 (t^2+1) ^ {1/2}}\,\ капелюх {\ mathbf {j}} +\ dfrac {4t} {5 (t^2+1) ^ {1/2}}\ капелюх {\ mathbf {k}}\\ [4pt]
&=−\ dfrag c {3t\,\ hat {\ mathbf {i}} +5\,\ капелюх {\ mathbf {j}} −4t\,\ капелюх {\ mathbf {k}}} {5\ sqrt {t^2+1}}. \ end {вирівнювати*}\]

Знову ж таки, одиничний дотичний вектор і основний одиничний нормальний вектор ортогональні один до одного для всіх значень$t$:

\ [\ почати {вирівнювати*}\ векс T (t) ·\ векс N (t) &=\ bigg (\ dfrac {3\,\ hat {\ mathbf {i}} −5t\,\ капелюх {\ mathbf {j}} −4\,\ капелюх {\ mathbf {k}}} {5\ sqrt {t^2+1}}\ великий) ·\ великий (−\ dfrac {3t\,\ капелюх {\ mathbf {i}} +5\,\ капелюх {\ mathbf {j}} −4t\,\ капелюх {\ mathbf {k}} {5\ sqrt {t^2+1}}\ bigg)\ [4pt]
&=\ dfrac {3 (−3т) −5т (−5) −4 (4т)} {25 (t^2+1)} \\ [4pt]
&=\ dfrac {−9t+25t−16t} {25 (t^2+1)}\\ [4pt]
&=0. \ end {вирівнювати*}\ nonumber\]

Останнє, оскільки$\vecs r(t)$ являє собою тривимірну криву, ми можемо обчислити бінормальний вектор, використовуючи$\ref{EqBinormal}$:

\ [\ почати {вирівнювати*}\ векс B (t) &=\;\ векс T (t) ×\ векс N (t)\\ [4pt]
&=\ почати {vmatrix}\ hat {\ mathbf {i}} &\ hat {\ mathbf {3} {5\ sqrt {t^2+1}} & −\ dfrac {5t} {5\ sqrt {t^2+1}} & −\ dfrac {4} {5\ sqrt {t^2+1}}\\\ dfrac {3t} {5\ sqrt {t^2+1}} & −\ dfrac {5} {5\ sqrt {t^2+1}} &\ dfrac {4t} {5\ sqrt {t^2+1}}\ кінець {матриця}\\ [4pt]
&=\ великий (\ dfrac {5t} {5\ sqrt {t^2+1}}\ bigg)\ bigg (\ dfrac {4t}} {5\ sqrt {t^2+1}}\ bigg) −\ bigg (−\ dfrac {4} {5\ sqrt {t^2+1}}\ bigg)\ bigg)\ bigg (−\ dfrac {5} {t^2+1}}\ великий)\,\ капелюх {\ mathbf {i}\
& -\ bigg (\ великий (\ drac {3} {5\ sqrt {t^2+1}}\ великий)\ великий (\ drac {4t} {5\ sqrt {t^2+1}}\ bigg) −\ bigg (−\ drac {4} {5\ sqrt {t^2+1}}\ bigg (−\ drac {3t} {5\ sqrt {t^2+1}}\ великий)\ великий)\,\ капелюх {\ mathbf {j}}\\
& +\ bigg (\ dfrac {3} {5\ sqrt {t^2+1}}\ bigg)\ bigg (-\ dfrac {5} {5\ sqrt {t^2+1}}\ великий)\ bigg (-\ dfrac {5} {5\ sqrt rt {t^2+1}}\ bigg) −\ великий (−\ drac {5t} {5\ sqrt {t^2+1}}\ великий)\ великий (−\ drac {3t} {5\ sqrt {t^2+1}}\ великий)\ bigg)\,\ капелюх {\ mathbf {k}}\ [4pt]
&=\ великий (\ dg\ frac {−20t^2−20} {25 (t^2+1)}\ великий)\,\ капелюх {\ mathbf {i}} +\ bigg (\ dfrac {−15t^2} {25 (t^2+1)}\ bigg)\,\ капелюх {\ mathbf {k}}\\ [4pt]
&= −20 великий (\ dfrac {t^2+1} {25 (t^2+1)}\ великий)\,\ капелюх {\ mathbf {i}} −15\ bigg (\ dfrac {t^2+1} {25 (t^2+1)}\ bigg)\ капелюх {\ mathbf {k}}\ [4pt]
&= −\ dfrac {4} {5}\,\ hat {\ mathbf {i}} −\ dfrac {3} {5}\,\ hat {\ mathbf {k}}. \ end {вирівнювати*}\ nonumber\]

Вправа$\PageIndex{4}$

Знайдіть одиничний вектор нормалі для векторно-значної функції$\vecs r(t)=(t^2−3t)\,\hat{\mathbf{i}}+(4t+1)\,\hat{\mathbf{j}}$ та оцініть його за адресою$t=2$.

Підказка: Спочатку знайдіть$\vecs T(t)$, потім використовуйте$\ref{EqNormal}$.
Відповідь: $\vecs N(2)=\dfrac{\sqrt{2}}{2}(\,\hat{\mathbf{i}}−\,\hat{\mathbf{j}})$

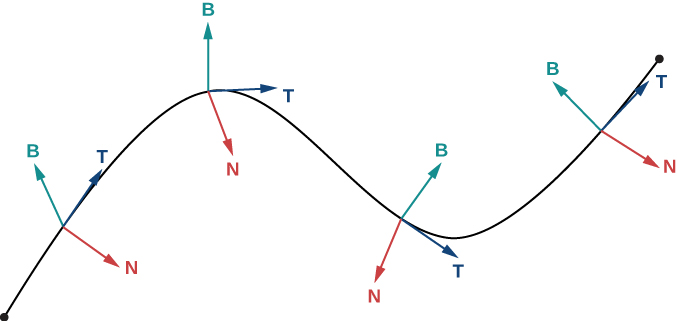
Для будь-якої гладкої кривої в трьох вимірах, яка визначається векторно-значною функцією, ми тепер маємо формули для одиничного тангенса вектора$\vecs T$, одиничного вектора$\vecs N$ нормалі та бінормального вектора$\vecs B$. Одиничний вектор нормалі і бінормальний вектор утворюють площину, яка перпендикулярна кривій в будь-якій точці кривої, званої нормальною площиною. Крім того, ці три вектори утворюють систему відліку в тривимірному просторі, звану фреймом відліку Френета (також називається рамкою TNB) (Рис.$\PageIndex{2}$). Останній, площина визначається векторами$\vecs T$ і$\vecs N$ утворює оскулюючу площину$C$ в будь-якій точці$P$ на кривій.

Ця цифра є графіком збільшення і зменшення кривої. Уздовж кривої в 4 різних точках знаходяться 3 вектора в кожній точці. Перший вектор позначений «T» і є дотичною до кривої в точці. Другий вектор позначений «N» і є нормальним до кривої в точці. Третій вектор позначений «B» і ортогональний T і N. — Малюнок$\PageIndex{2}$: На цьому малюнку зображена рамка відліку Френе. У кожній *$P$*точці тривимірної кривої одиничний тангенс, одиничний нормальний та бінормальний вектори утворюють тривимірну систему відліку.

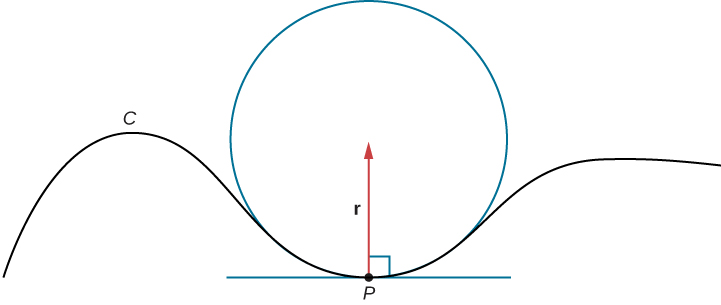
Припустимо, ми формуємо коло в оскулюючої площині точки$C$$P$ на кривій. Припустімо, що коло має ту саму кривизну, що і крива в точці,$P$ і нехай коло має радіус$r$. Потім задана кривизна кола$\frac{1}{r}$. $r$Назвемо радіус кривої кривої, і він дорівнює зворотній кривизні. Якщо це коло лежить на увігнутій стороні кривої і є дотичною до кривої в точці$P$, то це коло називається оскулюючий окружністю в$P$, як показано$C$ на малюнку$\PageIndex{3}$.

Ця цифра є графіком кривої з колом посередині. Дно кола таке ж, як частина кривої. Усередині кола знаходиться вектор з міткою «r». Вона починається в точці «P» на колі і вказує на радіус. Існує також відрізок лінії, перпендикулярний радіусу і дотичний до точки Р. — Малюнок$\PageIndex{3}$: У цьому оскуляційному колі коло дотичне до кривої$C$ в точці$P$ *і має однакову кривизну.*

Для отримання додаткової інформації про оскулюючі кола див. Цю демонстрацію кривизни та кручення, цю статтю про оскулюючі кола та це обговорення формул Серре.

Щоб знайти рівняння оскулюючого кола в двох вимірах, нам потрібно знайти тільки центр і радіус кола.

Приклад$\PageIndex{5}$: Finding the Equation of an Osculating Circle

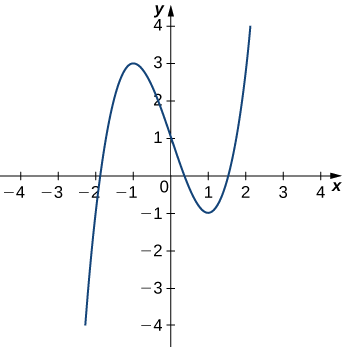
Знайти рівняння оскулюлюючої окружності кривої, визначеної функцією$y=x^3−3x+1$ на$x=1$.

Рішення

На малюнку$\PageIndex{4}$ показаний графік$y=x^3−3x+1$.

Ця цифра є графом кубічної функції y = x^3-3x+1. Крива збільшується, досягає максимуму при x = -1, зменшується, проходячи через вісь y на 1, потім досягаючи мінімуму при x =1, перш ніж знову збільшуватися. — Малюнок$\PageIndex{4}$: Ми хочемо знайти оскулюлюючу окружність цього графіка в точці, де$x=1$.

Для початку розрахуємо кривизну при$x=1$:

\[κ =\dfrac{|f″(x)|}{\bigg( 1+[f′(x)]^2 \bigg) ^{3/2}} = \dfrac{|6x|}{(1+[3x^2−3]^2)^{3/2}}. \nonumber \]

Це дає$κ=6$. Тому радіус оскулюючої окружності задається за допомогою$R=\frac{1}{κ}=\dfrac{1}{6}$. Далі потім обчислюємо координати центру кола. Коли$x=1$, нахил дотичної лінії дорівнює нулю. Тому центр оскулюючого кола знаходиться безпосередньо над точкою на графіку з координатами$(1,−1)$. Центр розташований за адресою$(1,−\frac{5}{6})$. Формула для кола з радіусом$r$ і центром$(h,k)$ задається за допомогою$(x−h)^2+(y−k)^2=r^2$. Тому рівняння оскулюючого кола є$(x−1)^2+(y+\frac{5}{6})^2=\frac{1}{36}$. Графік та його оскуляційний круг відображаються на наступному графіку.

Вправа$\PageIndex{5}$

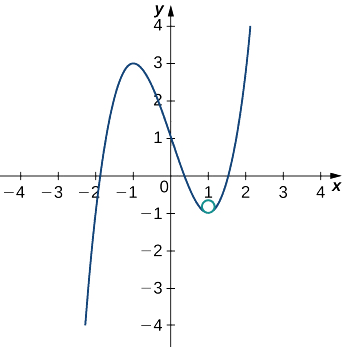
Знайти рівняння оскулюлюючої окружності кривої, визначеної векторно-значною функцією$y=2x^2−4x+5$ при$x=1$.

Підказка: Використовуйте$\ref{EqK4}$ для пошуку кривизни графіка, а потім намалюйте графік функції навколо,$x=1$ щоб допомогти візуалізувати коло по відношенню до графіка.

Відповідь

$κ =\frac{4}{[1+(4x−4)^2]^{3/2}}$

У$x=1$ точці кривизна дорівнює$4$. Тому радіус оскулюючого кола є$\frac{1}{4}$.

Графік цієї функції з'являється далі:

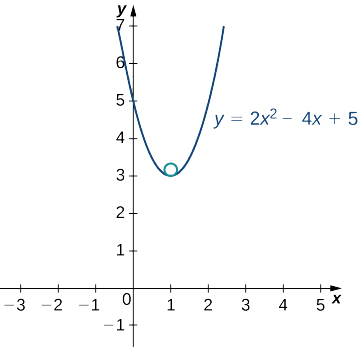
$Ця цифра є графіком функції y = 2x^2-4x+5. Крива являє собою параболу, що відкривається вгору вершиною в (1, 3).$

Вершина цієї параболи розташовується в точці$(1,3)$. Крім того, центр оскулюючого кола знаходиться безпосередньо над вершиною. Тому координати центру є$(1,\frac{13}{4})$. Рівняння оскулюючого кола дорівнює

$(x−1)^2+(y−\frac{13}{4})^2=\frac{1}{16}$.

Ключові концепції

Функція довжини дуги для векторно-значної функції обчислюється за інтегральною формулою$\displaystyle s(t)=\int_a^b ‖\vecs r′(t)‖\,dt $. Ця формула справедлива як в двох, так і в трьох вимірах.
Кривизна кривої в точці в двох або трьох вимірах визначається як кривизна вписаного кола в цій точці. Параметризація довжини дуги використовується при визначенні кривизни.
Існує кілька різних формул кривизни. Викривлення кола дорівнює зворотній його радіусу.
Основний блок нормального вектора$t$ при визначено бути
\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \nonumber \]
Бінормальний вектор at$t$ визначається як$\vecs B(t)=\vecs T(t)×\vecs N(t)$, де$\vecs T(t)$ - одиничний тангенсний вектор.
Кадр відліку Френета утворений одиничним дотичним вектором, головним одиничним нормальним вектором та бінормальним вектором.
Окуляційна окружність є дотичною до кривої в точці і має ту саму кривизну, що і дотична крива в цій точці.

Ключові рівняння

Довжина дуги кривої простору
$s= {\displaystyle \int _a^b} \sqrt{[f′(t)]^2+[g′(t)]^2+[h′(t)]^2} \,dt= {\displaystyle \int _a^b} ‖\vecs r′(t)‖\,dt$
Функція довжини дуги
$s(t)={\displaystyle \int _a^t} \sqrt{f′(u))^2+(g′(u))^2+(h′(u))^2} \,du \; or \; s(t)={\displaystyle \int _a^t}‖\vecs r′(u)‖\,du$
$κ=\frac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖} \; or \; κ=\frac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3} \; or \; κ=\frac{|y″|}{[1+(y′)^2]^{3/2}}$
Основна одиниця нормального вектора
$\vecs N(t)=\frac{\vecs T′(t)}{‖\vecs T′(t)‖}$
Бінормальний вектор
$\vecs B(t)=\vecs T(t)×\vecs N(t)$

Глосарій

функція довжини дуги: функція$s(t)$, яка описує довжину дуги кривої$C$ як функцію$t$

параметризація довжини дуги: репараметризація векторно-значної функції, у якій параметр дорівнює довжині дуги

бінормальний вектор: одиничний вектор, ортогональний до одиничного дотичного вектора та вектору одиниці нормалі

викривлення: похідна одиничного дотичного вектора по відношенню до параметра довжини дуги

Френета кадр відліку: (кадр TNB) — система відліку в тривимірному просторі, утворена одиничним дотичним вектором, одиничним нормальним вектором та бінормальним вектором

нормальна площина: площині, яка перпендикулярна до кривої в будь-якій точці на кривій

оскулюючий коло: коло, яка є дотичною до кривої$C$ в точці,$P$ і що розділяє ту ж кривизну

оскулююча площина: площину, визначену одиничним тангенсом і одиничним вектором нормалі

основна одиниця нормального вектора: вектор, ортогональний до одиничного дотичного вектора, заданий формулою$\frac{\vecs T′(t)}{‖\vecs T′(t)‖}$

радіус кривизни: зворотна кривизна

гладкий: криві, де векторно-значна функція$\vecs r(t)$ диференційовна з ненульовою похідною

Теорема: Формули довжини дуги для плоских і просторових кривих

Приклад\(\PageIndex{1}\): Finding the Arc Length

Вправа\(\PageIndex{1}\)

Теорема: Функція довжини дуги

Приклад\(\PageIndex{2}\): Finding an Arc-Length Parameterization

Вправа\(\PageIndex{2}\)

Теорема: Альтернативні формули кривизни

Доказ

Приклад\(\PageIndex{3}\): Finding Curvature

Вправа\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\): Finding the Principal Unit Normal Vector and Binormal Vector

Вправа\(\PageIndex{4}\)

Приклад\(\PageIndex{5}\): Finding the Equation of an Osculating Circle

Вправа\(\PageIndex{5}\)