11.3: Обчислення руху

Загальним використанням векторно-значних функцій є опис руху об'єкта в площині або в просторі. Функція$\vecs r(t)$ position дає позицію об'єкта в той час$t$. У цьому розділі досліджується, як похідні та інтеграли використовуються для вивчення руху, описаного такою функцією.

Визначення 73: Швидкість, швидкість і прискорення

$\vecs r(t)$Дозволяти бути функція положення в$\mathbb{R}^2$ або$\mathbb{R}^3$.

• Швидкість, що позначається$\vecs v(t)$, - це миттєва швидкість зміни положення; тобто

$$\vecs v(t) = \vecs r^\prime (t).$$

• Швидкість - це величина швидкості,

$$\text{speed} = \norm{\vecs v(t)}.$$

• Прискорення$\vecs a(t)$, що позначається, - це миттєва швидкість зміни швидкості; тобто

$$\vecs a(t) = \vecs v\,'(t) = \vecs r^{\prime\prime}(t).$$

Приклад$\PageIndex{1}$: Finding velocity and acceleration

Об'єкт рухається з функцією положення$\vecs r(t) = \langle t^2-t,t^2+t\rangle$$-3\leq t\leq 3$, де відстані вимірюються в футах, а час вимірюється в секундах.

1. Знайти$\vecs v (t)$ і$\vecs a (t)$.
2. Ескіз$\vecs r (t)$; сюжет$\vecs v(-1)$$\vecs a(-1)$,$\vecs v(1)$ і$\vecs a(1)$, кожен зі своєю початковою точкою у відповідній точці на графіку$\vecs r (t)$.
3. Коли швидкість об'єкта зводиться до мінімуму?

Рішення

1. Взявши похідні, знаходимо $$\vecs v (t) = \vecs r^\prime (t) =\langle 2t-1,2t+1\rangle \nonumber$$ і $$\quad \vecs a (t) = \vecs r^{\prime\prime}(t) = \langle 2,2\rangle. \nonumber$$ відзначаємо, що прискорення постійне.
   
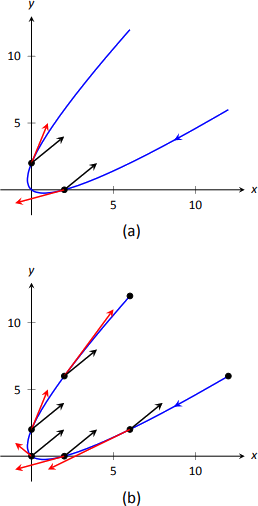
2. $\vecs v(-1) = \langle -3,-1\rangle$,$\vecs a(-1) = \langle 2,2\rangle$;$\vecs v(1) = \langle 1,3\rangle$,$\vecs a(1) = \langle 2,2\rangle$. Вони позначені на$\vecs r (t)$ малюнку$\PageIndex{1a}$.
   Ми можемо думати про прискорення як «витягування» вектора швидкості в певному напрямку. На$t=-1$, вектор швидкості вказує вниз і вліво; в$t=1$, вектор швидкості був витягнутий у$\langle 2,2\rangle$ напрямку і тепер спрямований вгору і вправо. На малюнку 11.15 (b) ми будуємо більше векторів швидкість/прискорення, що робить більш зрозумілим вплив прискорення на швидкість.
   Так$\vecs a (t)$ як постійна в цьому прикладі, так як$t$ зростає велика$\vecs v (t)$ стає майже паралельно$\vecs a (t)$. Наприклад, коли$t=10$$\vecs v(10) = \langle 19,21\rangle$, що майже паралельно$\langle 2,2\rangle$.
3. Швидкість об'єкта задається $$\norm{\vecs v (t)} = \sqrt{(2t-1)^2+(2t+1)^2} =\sqrt{8t^2+2}.$$ Щоб знайти мінімальну швидкість, ми могли б застосувати методи обчислення (наприклад, встановити похідну рівну 0 і вирішити для тощо)$t$, але ми можемо знайти її шляхом перевірки. Усередині квадратного кореня ми маємо квадратний, який мінімізується, коли$t=0$. Таким чином, швидкість зводиться до мінімуму$t=0$, зі швидкістю$\sqrt{2}$ ft/s. графік
   
   на малюнку$\PageIndex{1b}$ також передбачає, що швидкість тут зведена до мінімуму. Заповнені точки на графіку розташовані в цілих значеннях$t$ від$-3$ 3 до 3. Точки, які знаходяться далеко один від одного, означають, що об'єкт пройшов велику відстань за 1 секунду, що вказує на високу швидкість; точки, які знаходяться близько один від одного, означають, що об'єкт не подорожував далеко за 1 секунду, що вказує на низьку швидкість. Точки розташовані найближче поруч$t=0$, маючи на увазі, що швидкість зведена до мінімуму поблизу цього значення.

Малюнок$\PageIndex{1}$: Графік положення, швидкості та прискорення об'єкта у прикладі 11.3.1

Приклад$\PageIndex{2}$: Analyzing Motion

Два об'єкти йдуть однаковим шляхом з різною швидкістю далі$[-1,1]$. Функція положення для Object 1 є$\vecs r_1(t) = \langle t, t^2\rangle$; функція положення для Object 2$\vecs r_2(t) = \langle t^3, t^6\rangle$, де відстані вимірюються в футах, а час вимірюється в секундах. Порівняйте швидкість, швидкість і прискорення двох об'єктів на шляху.

Рішення

Почнемо з обчислення функції швидкості та прискорення для кожного об'єкта:

\ [\ begin {align*}
\ vecs v_1 (t) &=\ кут 1,2 т\ діапазон &\ векс v_2 (t) &=\ кут 3t^2,6t^5\ діапазон\\ [4pt]
\ vecs a_1 (t) &=\ кут 0,2\ діапазон &\ vecs a_2 (t) &=\ langle 6t ,30t^4\ діапазон
\ кінець {align*}\]

Ми відразу бачимо, що Object 1 має постійне прискорення, тоді як Object 2 - ні.

В$t=-1$, ми маємо$\vecs v_1(-1) = \langle 1,-2\rangle$ і$\vecs v_2(-1) = \langle 3,-6\rangle$; швидкість об'єкта 2 втричі більше, ніж у Об'єкта 1, і тому випливає, що швидкість об'єкта 2 втричі більше, ніж у Об'єкта 1 ($3\sqrt{5}$ft/s порівняно з$\sqrt{5}$ ft/s.)

Малюнок$\PageIndex{2}$: Побудова векторів швидкості та прискорення для Об'єкта 1 у прикладі 11.3.2

При$t=0$, швидкість об'єкта 1 є$\vecs v(1) = \langle 1,0\rangle$ і швидкість об'єкта 2 є$\vecs 0$! Це говорить нам, що Об'єкт 2 приходить до повної зупинки$t=0$.

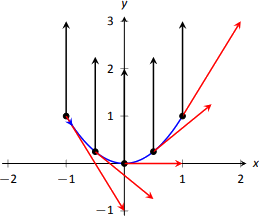
На малюнку$\PageIndex{2}$ ми бачимо вектори швидкості та прискорення для Об'єкта 1, побудовані для$t=-1, -1/2, 0, 1/2$ та$t=1$. Зауважте ще раз, як вектор постійного прискорення, здається, «тягне» вектор швидкості від вказівки вниз, вправо вгору, вправо. Ми могли б побудувати аналогічну картину для Object 2, але вектори швидкості та прискорення досить великі ($\vecs a_2(-1) = \langle -6,30\rangle$!)

Замість цього ми просто будуємо розташування Об'єкта 1 та 2 на інтервалах секунди, показаних на малюнку$\PageIndex{3a}$ та$\PageIndex{3b}$.$1/10^{\text{th}}$ Зверніть увагу, як$x$ -значення Object 1 збільшуються з постійною швидкістю. Це пов'язано з тим, що$x$ -компонент$\vecs a(t)$ дорівнює 0; у$x$ -компоненті немає прискорення. Точки розташовані не рівномірно; об'єкт рухається швидше поблизу$t=-1$ і$t=1$ поблизу$t=0$.

Рисунок$\PageIndex{3}$: Порівняння позицій об'єктів 1 та 2 у прикладі 11.3.2

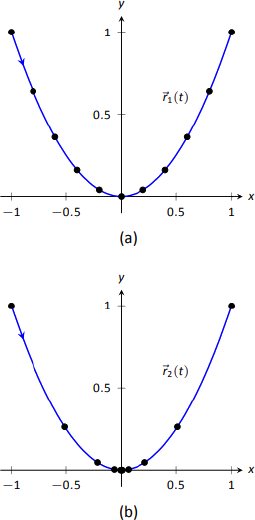
На малюнку ми бачимо точки$\PageIndex{3b}$, нанесені для Об'єкта 2. Зверніть увагу на велику зміну положення від$t=-1$ до$t=-0.9$; об'єкт починає рухатися дуже швидко. Однак він значно сповільнюється у нього наближається до походження, і доходить до повної зупинки$t=0$. Хоча схоже на те, що поблизу походження є 3 точки, насправді є 5 балів.

Оскільки об'єкти починаються і закінчуються в одному місці, вони мають однакове зміщення. Оскільки вони починаються і закінчуються одночасно, з однаковим зміщенням, вони мають однакову середню швидкість зміни (тобто мають однакову середню швидкість). Оскільки вони йдуть одним і тим же шляхом, у них однакова пройдена відстань. Незважаючи на те, що ці три вимірювання однакові, об'єкти, очевидно, подорожують шляхом дуже різними способами.

Приклад$\PageIndex{3}$: Analyzing the motion of a whirling ball on a string

Молодий хлопчик кружляє м'яч, прикріплений до мотузки, над головою по колу проти годинникової стрілки. Куля йде по круговому шляху і робить 2 обороти в секунду. Рядок має довжину 2ft.

1. Знайдіть функцію position$\vecs r(t)$, яка описує цю ситуацію.
2. Знайдіть прискорення м'яча і виведіть його фізичну інтерпретацію.
3. Дерево стоїть 10 футів перед хлопчиком. При яких$t$ -значеннях хлопчик повинен відпускати струну, щоб кулька потрапила в дерево?

Рішення

1. Куля кружиться по колу. Оскільки струна довжиною 2 фути, радіус кола дорівнює 2. Функція$\vecs r (t)= \langle 2\cos t, 2\sin t\rangle$ position описує коло з радіусом 2, центрований у початку, але робить повний оборот кожні$2\pi$ секунди, а не два обороти в секунду. Ми модифікуємо період тригонометричних функцій на 1/2 множенням$t$ на$4\pi$. Кінцева функція положення є таким чином $$\vecs r (t) = \langle 2\cos (4\pi t), 2\sin (4\pi t)\rangle.$$ (Покладіть це для того,$0\leq t\leq 1/2$ щоб переконатися, що один оборот зроблений за 1/2 секунди.)
2. Щоб знайти$\vecs a (t)$, виводимо$\vecs r (t)$ двічі. $$\begin{align*}\vecs v (t) = \vecs r^\prime (t) &= \langle -8\pi \sin (4\pi t), 8\pi \cos (4\pi t)\rangle\\[4pt] \vecs a (t) =\vecs r^{\prime\prime}(t) &= \langle -32\pi^2 \cos (4\pi t), -32\pi^2 \sin (4\pi t) \rangle \\[4pt]&= -32\pi^2\langle \cos (4\pi t), \sin (4\pi t)\rangle.\end{align*}$$
   
   Зверніть увагу, як$\vecs a (t)$ паралельно$\vecs r (t)$, але має різну величину і вказує в протилежну сторону. Чому це?
   
   Нагадаємо класичне рівняння фізики «$\times$Прискорення$=$ маси сили». Сила, що діє на масу, індукує прискорення (тобто маса рухається); прискорення, що діє на масу, індукує силу (гравітація дає нашій масі вага). При цьому сила і прискорення тісно пов'язані між собою. Рухомий куля «хоче» подорожувати по прямій. Чому м'яч в нашому прикладі рухається по колу? Вона кріпиться до руки хлопчика мотузкою. Струна прикладає силу до м'яча, впливаючи на його рух: струна прискорює м'яч. Це не прискорення в сенсі «він подорожує швидше»; скоріше, це прискорення змінює швидкість м'яча. В якому напрямку застосовується ця сила/прискорення? У напрямку струни, у напрямку до руки хлопчика.
   
   Величина прискорення пов'язана зі швидкістю, з якою рухається м'яч. Куля, що кружиться швидко, швидко змінює напрямк/швидкість. Коли швидкість швидко змінюється, прискорення повинно бути «великим».
   
3. Коли хлопчик відпускає струну, струна більше не докладає сили до м'яча, тобто прискорення є$\vecs 0$ і м'яч тепер може рухатися по прямій лінії в напрямку$\vecs v(t)$.
   
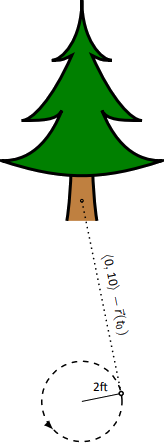
   Нехай$t=t_0$ буде час, коли хлопчик відпускає струну. М'яч буде знаходитися при$\vecs r(t_0)$, рухаючись у напрямку$\vecs v(t_0)$. Ми хочемо знайти$t_0$ так, щоб цей рядок містив точку$(0,10)$ (так як дерево 10 футів безпосередньо перед хлопчиком).
   
   Існує багато способів знайти це значення часу. Ми вибираємо той, який є відносно простим обчислювальним шляхом. Як показано на малюнку$\PageIndex{4}$, вектор від точки випуску до дерева є$\langle 0,10\rangle - \vecs r(t_0)$. Цей відрізок лінії дотичний до кола, що означає, що він також перпендикулярний до$\vecs r(t_0)$ себе, тому їх точковий добуток дорівнює 0. $$\begin{align*}\vecs r(t_0) \cdot \big(\langle 0,10\rangle - \vecs r(t_0)\big) &=0\\[4pt] \langle 2\cos (4\pi t_0), 2\sin (4\pi t_0)\rangle \cdot \langle -2\cos(4\pi t_0),10-2\sin (4\pi t_0)\rangle &=0\\[4pt]-4\cos^2(4\pi t_0) + 20\sin (4\pi t_0)-4\sin^2(4\pi t_0) &= 0\\[4pt]20\sin (4\pi t_0) - 4 &=0\\[4pt] \sin (4\pi t_0) &=1/5\\[4pt]4\pi t_0 &= \sin^{-1}(1/5)\\[4pt]4\pi t_0 &\approx 0.2 + 2\pi n, \end{align*}$$ де$n$ - ціле число. Рішення для$t_0$ нас є: $$t_0 \approx 0.016 + n/2\nonumber$$ Це чудова формула. Кожні 1/2 секунди після$t=0.016$ s хлопчик може звільнити струну (так як м'яч робить 2 обороти в секунду, у нього є два шанси кожну секунду випустити м'яч).

Малюнок$\PageIndex{4}$: Моделювання польоту кулі в прикладі 11.3.3

Приклад$\PageIndex{4}$: Analyzing motion in space

Об'єкт рухається по спіралі з функцією положення$\vecs r (t) = \langle \cos t, \sin t, t\rangle$, де відстані вимірюються в метрах, а час - у хвилинах. Опишіть швидкість і прискорення об'єкта в часі$t$.

Рішення
С$\vecs r (t) = \langle \cos t,\sin t, t\rangle$, у нас є:

\ [\ begin {align*}
\ vecs v (t) &=\ ланголь -\ sin t,\ cos t, 1\ rangle\ quad\ text {і}\\ [4pt]
\ vecs a (t) &=\ лангель -\ cos t, -\ sin t, 0\ діапазон.
\ end {вирівнювати*}\]

Швидкість об'єкта -$\norm{\vecs v (t)} = \sqrt{(-\sin t)^2+\cos^2t+1} = \sqrt{2}$ м/хв; він рухається з постійною швидкістю. Зверніть увагу, що об'єкт не розганяється в$z$ -напрямку, а навпаки рухається вгору з постійною швидкістю 1м/хв.

Об'єкти в прикладах 11.3.3 і 11.3.4 подорожували з постійною швидкістю. Тобто$\norm{\vecs v (t)} = c$ для якоїсь постійної$c$. Нагадаємо теорему 93, яка стверджує, що якщо векторно-значна функція$\vecs r (t)$\ має постійну довжину, то$\vecs r (t)$\ перпендикулярна її похідній:$\vecs r (t)\cdot\vecs r^\prime (t) = 0$. У цих прикладах функція швидкості має постійну довжину, тому можна зробити висновок, що швидкість перпендикулярна прискоренню:$\vecs v (t)cdot\vecs a (t) = 0$. Швидка перевірка підтверджує це.

Є інтуїтивне розуміння цього. Якщо прискорення паралельно швидкості, то воно впливає лише на швидкість об'єкта; воно не змінює напрямок руху. (Наприклад, розглянемо випав камінь. Прискорення і швидкість паралельні - прямо вниз - і напрямок швидкості ніколи не змінюється, хоча швидкість зростає.) Якщо прискорення не перпендикулярно швидкості, то відбувається деяке прискорення в напрямку руху, що впливає на швидкість. Якщо швидкість постійна, то прискорення має бути ортогональним швидкості, так як воно потім впливає тільки на напрямок, а не швидкість.

ключова ідея: 52 об'єкти з постійною швидкістю

Якщо об'єкт рухається з постійною швидкістю, то його вектори швидкості і прискорення ортогональні. Тобто,$\vecs v (t)cdot\vecs a (t)=0$.

рух снаряда

Важливим застосуванням векторно-значних функцій положення є рух снаряда: рух об'єктів тільки під впливом сили тяжіння. Ми будемо вимірювати час в секундах, а відстані будуть або в метрах, або футах. Ми покажемо, що можемо повністю описати шлях такого об'єкта, знаючи його початкове положення і початкову швидкість (тобто, де він знаходиться і куди йде.)

Припустимо, об'єкт має початкове положення$\vecs r(0) = \langle x_0,y_0\rangle$ і початкову швидкість$\vecs v(0) = \langle v_x,v_y\rangle$. Прийнято переписувати$\vecs v(0)$ в плані його швидкості$v_0$ і напрямку$\vecs u$, де$\vecs u$ - одиничний вектор. Згадати всі одиничні вектори в$\mathbb{R}^2$ можна записати як$\langle \cos \theta,\sin \theta\rangle$, де$\theta$ є міра кута проти годинникової стрілки від$x$ -осі. (Ми називаємо$\theta$ кутом піднесення.) Таким чином$\vecs v(0) = v_0\langle \cos \theta,\sin \theta\rangle.$

Оскільки відомо прискорення об'єкта, а саме$\vecs a (t) = \langle 0,-g\rangle$, де$g$ гравітаційна константа, ми можемо знайти$\vecs r (t)$ знаючи дві наші початкові умови. Спочатку знаходимо\ (\ vecs v (t)):

Примітка

У цьому тексті ми використовуємо$g=32$ ft/s при використанні імперських одиниць, і$g=9.8$ м/с при використанні одиниць СІ.

\ [\ почати {вирівнювати*}
\ векс v (t) &=\ int\ vecs a (t) dt\\ [4pt]
\ vecs v (t) &=\ int\ langle 0, -g\ діапазон dt\\ [4pt]
\ vecs v (t) &=\ langle 0, -gt\ діапазон +\ vecs C
\ end {align*}\

Знаючи$\vecs v(0) = v_0\langle \cos \theta,\sin \theta\rangle$, у нас$\vecs C = v_0\langle \cos t,\sin t\rangle$ і так

$$\vecs v(t) = \langle v_0\cos \theta, -gt+v_0\sin\theta\rangle.$$

Ми інтегруємося ще раз, щоб знайти$\vecs r (t)$:

\ [\ почати {align*}
\ векс r (t) &=\ int\ vecs v (t) dt\\\ [4pt]
\ vecs r (t) &=\ int\ ланкут v_0\ cos\ тета, -gt+v_0\ sin\ тета\ діапазон dt\\ [4pt]
\ vecs r (t) &=\ langle\ великий (v_0 cos\ тета\ великий) t, -\ dfrac12gt^2+\ великий (v_0\ sin\ тета\ великий) t\ діапазон +\ vecs C\\ [4pt]
\ text {Знаючи$\vecs r(0) = \langle x_0,y_0\rangle$, робимо висновок$\vecs C = \langle x_0,y_0\rangle$ і} &\\ [4pt]
\ vecs r (t) &=\ лангол\ великий (v_0\ cos\ тета\ великий) t+x_0\, -\ dfrac12gt^2+\ big (v_0\ sin\ theta\ big) t+y_0\\ rangle.
\ end {вирівнювати*}\]

Ключова ідея 53: Рух снаряда

Функція положення снаряда, що рухається з початкового положення$\vecs r_0=\langle x_0,y_0\rangle$, з початковою швидкістю$v_0$, з кутом підйому$\theta$ і нехтуючи всіма прискореннями, але гравітація

$$\vecs r (t) = \langle \big(v_0\cos \theta\big)t+x_0\ , -\dfrac12gt^2+\big(v_0\sin\theta\big)t+y_0\ \rangle.$$

Letting$\vecs v_0 = v_0\langle \cos \theta,\sin \theta\rangle$, (\ vecs r (t)\) можна записати як

$$\vecs r (t) = \langle 0,-\dfrac12gt^2\rangle + \vecs v_0t+\vecs r_0.$$

Ми продемонструємо, як використовувати цю функцію position у наступних двох прикладах.

Приклад$\PageIndex{5}$: Projectile Motion

Сідней стріляє її Red Ryder bb гармати через рівень землі з висоти 4ft, де ствол гармати робить$5^\circ$ кут з горизонталлю. Знайдіть, наскільки далеко bb подорожує перед посадкою, припускаючи, що bb звільняється з рекламованою швидкістю 350ft/s і ігноруючи опір повітря.

Рішення

Пряме застосування Key Idea 53 дає

\ [\ почати {вирівнювати*}
\ vecs r (t) &=\ лангове (350\ cos 5^\ коло) t, -16t^2 + (350\ sin 5^\ коло) t + 4\ діапазон\\ [4pt]
&\ приблизно\ langle 346.67t, -16t^2+30.50t+4\ діапазон,
\ кінець {вирівнювати*}]

де ми встановлюємо її початкове положення бути$\langle 0,4\rangle$.
Нам потрібно знайти, коли bb приземлиться, тоді ми зможемо знайти де. Ми досягаємо цього, встановивши$y$ -компонент рівний 0 і вирішивши для$t$:

\ [\ почати {вирівнювати*}
-16t^2+30.50т+4 &= 0\\ [4pt]
t &=\ dfrac {-30.50\ pm\ sqrt {30.50^2-4 (-16) (4)}} {-32}\ [
4pt] t &\ приблизно 2,03 с.
\ end {вирівнювати*}\]

(Ми відкинули негативне рішення, яке вийшло з нашого квадратного рівняння.)

Ми виявили, що bb приземляється 2.03s після стрільби; з$t=2.03$, ми знаходимо$x$ -компонент нашої позиції функції$346.67(2.03) = 703.74$ ft. Bb приземляється приблизно за 700 метрів від готелю.

Приклад$\PageIndex{6}$: Projectile Motion

Алекс тримає bb пістолет своєї сестри на висоті 3ft і хоче стріляти в ціль, яка знаходиться на 6 футів над землею, 25 футів. Під яким кутом він повинен тримати пістолет, щоб вразити свою ціль? (Ми все ще припускаємо, що дульна швидкість становить 350ft/s.)

Рішення

Функція позиції для шляху bb Алекса дорівнює

$$\vecs r (t) = \langle (350\cos \theta)t, -16t^2+(350\sin\theta)t+3\rangle. \nonumber$$

Нам потрібно знайти$\theta$ так, що$\vecs r (t)$ =\ langle 25,6\ rangle\) для деякого значення$t$. Тобто ми хочемо знайти$\theta$ і$t$ таке, що

$$(350\cos\theta)t = 25 \quad \text{and}\quad -16t^2+(350\sin\theta)t+3 = 6. \nonumber$$

Це не банально (хоча і не «важко»). Починаємо з вирішення кожного рівняння для$\cos\theta$ і$\sin \theta$, відповідно.

$$\cos\theta = \dfrac{25}{350t} \quad \text{and} \quad \sin\theta = \dfrac{3+16t^2}{350t}. \nonumber$$

Використовуючи Піфагорійську ідентичність$\cos^2\theta+\sin^2\theta=1$, ми маємо

$$\left(\dfrac{25}{350t}\right)^2 + \left(\dfrac{3+16t^2}{350t}\right)^2 =1 \nonumber$$

Помножте обидві сторони на$(350t)^2$:

$$\begin{align*}25^2 + (3+16t^2)^2 &=350^2t^2\\[4pt] 256t^4-122,404t^2+634 &=0.\end{align*}$$

Це квадратичний в$t^2$. Тобто ми можемо застосувати квадратичну формулу, щоб знайти$t^2$, потім вирішити для$t$ себе.

\ [\ почати {вирівнювати*}
t^2 &=\ dfrac {122,404\ пм\ sqrt {122,404 ^ 2-4 (256) (634)}} {512}\ [4pt]
t^2 &= 0,0052,\ 478.135\\ [
4pt] t &=\ вечора 0.072,\\ pm 21.866
\ кінець {вирівнювати*}\]

Очевидно, що негативні$t$ значення не відповідають нашому контексту, тому ми маємо$t=0.072$ і$t=21.866$. Використовуючи$\cos \theta = 25/(350 t)$, ми можемо вирішити для$\theta$:

\ [\ почати {вирівнювати*}
\ тета &=\ cos^ {-1}\ лівий (\ dfrac {25} {350\ cdot 0.072}\ праворуч)\ квадратний\ текст {і}\ квад\ cos^ {-1}\ ліворуч (\ dfrac {25} {350\ cdot 21.866}\ праворуч)\\ [4pt]
\ тета = 7.03^\ circ квад\ текст {і}\ квад 89.8^\ circ.
\ end {вирівнювати*}\]

Алекс має два варіанти кута. Він може тримати гвинтівку під кутом приблизно$7^\circ$ з горизонталлю і вразити свою ціль$0.07$ s після стрільби, або він може тримати свою гвинтівку майже прямо вгору, з кутом$89.8^\circ$, де він вдарить свою ціль близько 22 секунд пізніше. Перший варіант - це явно той варіант, який він повинен вибрати.

Пройдена відстань

Розглянемо водія, який встановлює свій круїз - контроль на 60 миль/год, і їде з цією швидкістю протягом години. Ми можемо запитати:

1. Як далеко проїхав водій?
2. Наскільки далеко від її вихідного положення знаходиться водій?

На першу легко відповісти: вона проїхала 60 миль. На друге неможливо відповісти наведеними відомостями. Ми не знаємо, чи їздила вона по прямій, по овальній іподромі або по повільно звивистій трасі.

Це підкреслює важливий факт: щоб обчислити пройдену відстань, нам потрібно лише знати швидкість, задану$\norm{\vecs v (t)}$.

Теорема 96: Пройдена відстань

$\vecs v (t)$Дозволяти функція швидкості для рухомого об'єкта. Відстань, яку долає об'єкт на$[a,b]$, становить:

$$\text{distance traveled} = \int_a^b \norm{\vecs v (t)} dt .$$

Зауважте, що це лише повторення теореми 95: довжина дуги така ж, як пройдена відстань, тільки що розглядається в іншому контексті.

Приклад$\PageIndex{7}$: Distance Traveled, Displacement, and Average Speed

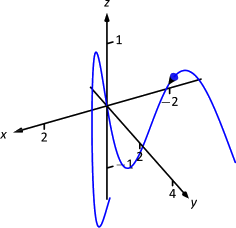
Частинка рухається в просторі з$\vecs r (t) = \langle t,t^2,\sin (\pi t)\rangle$ включеною функцією положення$[-2,2]$, де$t$ вимірюється в секундах, а відстані - в метрах. Знайти:

1. Відстань, пройдену частинкою на$[-2,2]$.
2. Зсув частинки на$[-2,2]$.
3. Середня швидкість частинки.

Рішення

1. Ми використовуємо теорему 96 для встановлення інтеграла: $$\begin{align*}\text{distance traveled} &= \int_{-2}^2 \norm{\vecs v (t)} dt \\[4pt]&= \int_{-2}^2 \sqrt{1+(2t)^2+ \pi^2\cos^2(\pi t)} dt .\end{align*}$$ Це не може бути вирішено з точки зору елементарних функцій, тому ми перейдемо до числового інтегрування, знаходячи відстань 12,88 м.
2. Зсув - це вектор $$\vecs r(2)-\vecs r(-2) = \langle 2,4,0\rangle - \langle -2,4,0\rangle = \langle 4,0,0\rangle. \nonumber$$ Тобто частка закінчується$x$ -значенням, збільшеним на 4, а з$y$ - і$z$ -значеннями однаковими (див. Рис.$\PageIndex{5}$).
3. Вище ми виявили, що частинка подорожувала 12,88 м протягом 4 секунд. Ми можемо обчислити середню швидкість діленням: 12,88/4 = 3,22 м/с,
   
   ми також повинні розглянути визначення 22 розділу 5.4, в якому сказано, що середнє значення функції$f$$[a,b]$ увімкнено$\dfrac{1}{b-a}\int_a^b f(x)\ dx$. У нашому контексті середнє значення швидкості - $$\text{average speed} = \dfrac{1}{2-(-2)}\int_{-2}^2 \norm{\vecs v (t)} dt \approx \dfrac14 12.88 = 3.22\text{m/s}. \nonumber$$
   
   Примітка, як фізичний контекст частинки, що подорожує, надає значення більш абстрактному поняттю, вивченому раніше.

Малюнок$\PageIndex{5}$: Шляхи частинки в прикладі 11.3.7

У Визначенні 22 глави 5 ми визначили середнє значення функції$f(x)$ on$[a,b]$ to be

$$\dfrac{1}{b-a}\int_a^bf(x) dx.$$

Зверніть увагу, як у прикладі 11.3.7 ми обчислили середню швидкість як

$$\dfrac{\text{distance traveled}}{\text{travel time}} = \dfrac1{2-(-2)}\int_{-2}^2\norm{\vecs v (t)} dt ;$$

тобто ми якраз знайшли середнє значення$\norm{\vecs v (t)}$ по$[-2,2]$.

Аналогічно, задана функція положення$\vecs r (t)$, середня швидкість$[a,b]$ на

$$\dfrac{\text{displacement}}{\text{travel time}} = \dfrac1{b-a}\int_a^b \vecs{r}\,'(t) dt = \dfrac{\vecs r(b)-\vecs r(a)}{b-a};$$

тобто це середнє значення$\vecs r\,'(t)$, або$\vecs v (t)$, на$[a,b]$.

KEY IDEA 54: Середня швидкість, Середня швидкість

$\vecs r(t)$Дозволяти функція безперервної позиції на відкритому інтервалі,$I$ що містить$a<b$.

• Середня швидкість становить:

$$\dfrac{\text{distance traveled}}{\text{travel time}} = \dfrac{\int_a^b \norm{\vecs v (t)} dt }{b-a} = \dfrac1{b-a}\int_a^b\norm{\vecs v (t)} dt .$$

• Середня швидкість становить:

$$\dfrac{\text{displacement}}{\text{travel time}} = \dfrac{\int_a^b \vecs{r}\,'(t) dt }{b-a} = \dfrac1{b-a}\int_a^b\vecs{r}\,'(t) dt .$$

Наступні два розділи досліджують більше властивостей графіків векторно-значних функцій, і ми застосуємо ці нові ідеї до того, що ми щойно дізналися про рух.