3.4: Похідні як темпи змін

Last updated
Save as PDF

Page ID: 62262

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте нове значення величини зі старого значення та суми зміни.
Розрахуйте середню швидкість зміни і поясніть, чим вона відрізняється від миттєвої швидкості зміни.
Застосовуйте швидкість зміни до переміщення, швидкості та прискорення об'єкта, що рухається по прямій лінії.
Прогнозуйте майбутнє населення від теперішнього значення і темпів приросту населення.
Використовуйте деривативи для розрахунку граничних витрат і доходів у бізнес-ситуації.

У цьому розділі ми розглянемо деякі застосування похідної, зосередившись на інтерпретації похідної як швидкості зміни функції. Ці програми включають прискорення та швидкість у фізиці, темпи зростання населення в біології та граничні функції в економіці.

Сума зміни формули

Одним із застосувань для похідних є оцінка невідомого значення функції в точці за допомогою відомого значення функції в певній точці разом із швидкістю її зміни у заданій точці. Якщо$f(x)$ функція визначена на інтервалі$[a,a+h]$, то величина зміни$f(x)$ за інтервал є зміною$y$ значень функції за цей інтервал і задається

\[f(a+h)−f(a). \nonumber \]

Середня швидкість зміни функції$f$ за той самий інтервал - це відношення величини зміни за цей інтервал до відповідної зміни$x$ значень. Це дається

\[\frac{f(a+h)−f(a)}{h}. \nonumber \]

Як ми вже знаємо, миттєва швидкість зміни$f(x)$ at$a$ є його похідною

\[f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}. \nonumber \]

Для невеликих значень досить$h$,$f′(a)≈\frac{f(a+h)−f(a)}{h}$. Потім ми можемо вирішити$f(a+h)$ для отримання суми зміни формули:

\[f(a+h)≈f(a)+f′(a)h. \label{linapprox} \]

Ми можемо використовувати цю формулу, якщо знаємо тільки$f(a)$$f′(a)$ і бажаємо оцінити значення$f(a+h)$. Наприклад, ми можемо використовувати поточне населення міста та темпи його зростання, щоб оцінити його населення найближчим часом. Як ми бачимо на малюнку$\PageIndex{1}$, ми$f(a+h)$ наближаємося$y$ координатою при a+h на лінії дотичній до$f(x)$ at$x=a$. Зверніть увагу, що точність цієї оцінки залежить$h$ як від величини, так і від величини$f′(a)$.

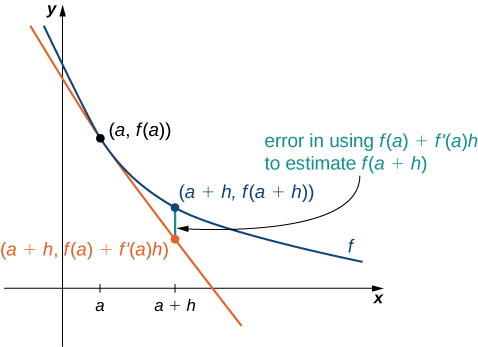
На декартовій координатній площині з a та a + h позначені на осі x графіком функції f. Вона проходить через (a, f (a)) і (a + h, f (a + h)). Пряма лінія проводиться через (a, f (a)), а її нахил є похідною в цій точці. Ця пряма проходить через (a + h, f (a) + f' (a) h). Існує відрізок лінії, що з'єднує (a + h, f (a + h)) і (a + h, f (a) + f' (a) h), і позначено, що це помилка у використанні f (a) + f' (a) h для оцінки f (a + h). — Малюнок$\PageIndex{1}$: Нове значення зміненої величини дорівнює початковому значенню плюс швидкість зміни на інтервал зміни:$f(a+h)≈f(a)+f′(a)h.$

Приклад$\PageIndex{1}$: Estimating the Value of a Function

Якщо$f(3)=2$ і$f′(3)=5$, прикиньте$f(3.2)$.

Рішення

Почніть з пошуку$h$. Ми маємо$h=3.2−3=0.2.$ Таким чином,

$f(3.2)=f(3+0.2)≈f(3)+(0.2)f′(3)=2+0.2(5)=3.$

Вправа$\PageIndex{1}$

Дано$f(10)=−5$ і$f′(10)=6$, кошторис$f(10.1)$.

Підказка: Використовуйте той самий процес, що і в попередньому прикладі.

Відповідь: $−4.4$

Рух вздовж лінії

Іншим використанням похідної є аналіз руху вздовж лінії. Ми описали швидкість як швидкість зміни положення. Якщо взяти похідну від швидкості, ми можемо знайти прискорення, або швидкість зміни швидкості. Також важливо ввести уявлення про швидкість, яка є величиною швидкості. Таким чином, можна викласти наступні математичні визначення.

Визначення

$s(t)$Дозволяти функція, що дає положення об'єкта в момент t.

Швидкість руху об'єкта в часі$t$ задається за допомогою$v(t)=s′(t)$.
Швидкість об'єкта в часі$t$ задається по$|v(t)|$.
Прискорення об'єкта при$t$ задається за допомогою$a(t)=v′(t)=s''(t)$.

Приклад$\PageIndex{2}$: Comparing Instantaneous Velocity and Average Velocity

М'яч скидається з висоти 64 футів. Його висота над землею (в футах)$t$ секунди пізніше задається$s(t)=−16t^2+64$.

$На декартовій координатній площині графується функція s (t) = −16t2 + 64. Ця функція починається з (0, 64) і зменшується до (0, 2).$

Яка миттєва швидкість кулі при ударі про землю?
Яка середня швидкість при її падінні?

Рішення

Перше, що потрібно зробити, це визначити, скільки часу потрібно м'ячу, щоб досягти землі. Для цього встановлюємо$s(t)=0$. Вирішуючи$−16t^2+64=0$, отримуємо$t=2$, тому потрібно 2 секунди, щоб м'яч досяг землі.

Миттєва швидкість кулі, коли він б'є об землю, є$v(2)$. Так як$v(t)=s′(t)=−32t$, отримуємо$v(t)=−64$ ft/s.
Середня швидкість м'яча під час його падіння дорівнює

$v_{ave}=\frac{s(2)−s(0)}{2−0}=\frac{0−64}{2}=−32$фут/с.

Приклад$\PageIndex{3}$: Interpreting the Relationship between $v(t)$ and $a(t)$

Частка рухається вздовж осі координат в позитивному напрямку вправо. Свою позицію в часі$t$ задає$s(t)=t^3−4t+2$. Знайдіть$v(1)$$a(1)$ і використовуйте ці значення, щоб відповісти на наступні питання.

Чи рухається частинка зліва направо або справа наліво під час$t=1$?
Частинка прискорюється або сповільнюється в часі$t=1$?

Рішення

Почніть з пошуку$v(t)$ і$a(t)$.

$v(t) = s'(t) = 3t^2 - 4$і$a(t)=v′(t)=s''(t)=6t$.

Оцінюючи ці функції при$t=1$, отримаємо$v(1)=−1$ і$a(1)=6$.

$v(1)<0$Тому що частка рухається справа наліво.
Тому що$v(1)<0$ і$a(1)>0$, швидкість і прискорення діють в протилежних напрямках. Іншими словами, частка прискорюється в напрямку, протилежному напрямку, в якому вона рухається, викликаючи$|v(t)|$ зменшення. Частинка сповільнюється.

Приклад$\PageIndex{4}$: Position and Velocity

Положення частинки, що рухається вздовж осі координат, задається$s(t)=t^3−9t^2+24t+4,\; t≥0.$

Знайти$v(t)$.
В який час (и) частинка знаходиться в стані спокою?
На яких часових інтервалах частка рухається зліва направо? Справа наліво?
Використовуйте отриману інформацію для ескізу шляху частинки вздовж координатної осі.

Рішення

а Швидкість є похідною від функції положення:

$v(t)=s′(t)=3t^2−18t+24.$

б. частинка знаходиться в стані спокою$v(t)=0$, коли, так встановлено$3t^2−18t+24=0$. Факторинг лівої частини рівняння виробляє$3(t−2)(t−4)=0$. Вирішуючи, виявляємо, що частка знаходиться в спокої при$t=2$ і$t=4$.

c Частка рухається зліва направо, коли$v(t)>0$ і справа наліво, коли$v(t)<0$. Малюнок$\PageIndex{2}$ дає аналіз знака$v(t)$ for$t≥0$, але він не представляє осі, по якій рухається частка.

Числовий рядок, позначений 0, 2 та 4. Між 0 і 2 є знак плюс. Вище 2 є 0. Між 2 і 4 є негативний знак. Над 4 є 0. Після 4 з'являється знак плюс і v (t). — Малюнок:$\PageIndex{2}$ Знак$v(t)$ of визначає напрямок частинки.

Починаючи з$3t^2−18t+24>0$$[0,2)∪(4,+∞)$ цього моменту, частка рухається зліва направо на цих проміжках.
Починаючи з$3t^2−18t+24<0$ цього моменту$(2,4)$, частка рухається справа наліво на цьому проміжку.

d Перш ніж ми зможемо намалювати графік частинки, нам потрібно знати її положення в той час, коли вона починає рухатися,$(t=0)$ і в той час, коли вона змінює напрямок$(t=2,4)$. У нас є$s(0)=4$$s(2)=24$, і$s(4)=20$. Це означає, що частка починається на осі координат$4$ і змінює напрямок на осі координат$24$ і$20$ на осі координат. Шляхи частинки показані на осі координат на рис$\PageIndex{3}$.

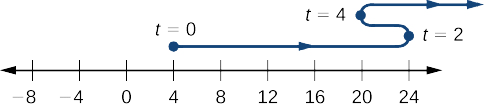
Задано числовий рядок і над ним рядок змій, починаючи з t = 0 вище 4 на числовому рядку. Тоді рядок при t = 2 вище 24 на числовому рядку. Потім лінія зменшується при t = 4, щоб бути вище 20 на числовій лінії, в цей момент лінія знову змінює напрямок і збільшується на невизначений час. — Малюнок$\PageIndex{3}$: Шляху частинки можна визначити шляхом аналізу$v(t)$.

Вправа$\PageIndex{2}$

Частка рухається вздовж осі координат. Свою позицію в часі$t$ задає$s(t)=t^2−5t+1$. Чи рухається частинка справа наліво або зліва направо в той час$t=3$?

Підказка: Знайдіть$v(3)$ і подивіться на знак.

Відповідь: зліва направо

Зміна населення

Окрім аналізу швидкості, швидкості, прискорення та положення, ми можемо використовувати похідні для аналізу різних типів популяцій, включаючи такі різноманітні, як колонії бактерій та міста. Ми можемо використовувати поточне населення разом із темпами зростання, щоб оцінити чисельність населення в майбутньому. Темпи приросту населення - це швидкість зміни популяції і, отже, можуть бути представлені похідною від чисельності населення.

Визначення

Якщо$P(t)$ кількість суб'єктів, присутніх у популяції, то темпи приросту населення визначаються як$P′(t)$.$P(t)$

Приклад$\PageIndex{5}$: Estimating a Population

Населення міста збільшується в три рази кожні 5 років. Якщо його нинішнє населення становить 10 000, якою буде його приблизна чисельність населення через 2 роки?

Рішення

Нехай$P(t)$ буде населення (в тисячах)$t$ років відтепер. Таким чином, ми знаємо, що$P(0)=10$ і виходячи з інформації, ми передбачаємо$P(5)=30$. Тепер$P′(0)$ оцінюємо, поточні темпи зростання, використовуючи

$P′(0)≈\frac{P(5)−P(0)}{5−0}=\frac{30−10}{5}=4$.

Застосовуючи Equation\ ref {linprox} to$P(t)$, ми можемо оцінити чисельність населення через 2 роки, написавши

$P(2)≈P(0)+(2)P′(0)≈10+2(4)=18$;

Таким чином, через 2 роки чисельність населення становитиме 18 000.

Вправа$\PageIndex{3}$

Нинішнє населення колонії комарів, як відомо, становить 3000; тобто$P(0)=3,000$. Якщо$P′(0)=100$, оцінити чисельність популяції в 3 дні, де$t$ вимірюється в днях.

Підказка: Використовувати$P(3)≈P(0)+3P′(0)$

Відповідь: 3 300

Зміни у витратах і доходах

Окрім аналізу руху вздовж лінії та зростання населення, похідні інструменти корисні для аналізу змін витрат, доходів та прибутку. Поняття граничної функції поширене в сферах бізнесу та економіки і має на увазі використання похідних. Гранична вартість є похідною від функції витрат. Маржинальний дохід є похідною від функції доходу. Маржинальний прибуток - це похідна від функції прибутку, яка базується на функції витрат та функції доходу.

Визначення

Якщо$C(x)$ це собівартість виробництва$x$ виробів, то гранична собівартість$MC(x)$ становить$MC(x)=C′(x)$.
Якщо$R(x)$ це дохід, отриманий від продажу$x$ предметів, то граничний дохід$MR(x)$ становить$MR(x)=R′(x)$.
Якщо$P(x)=R(x)−C(x)$ це прибуток, отриманий від продажу$x$ предметів, то $MP(x)$граничний прибуток визначається як$MP(x)=P′(x)=MR(x)−MC(x)=R′(x)−C′(x)$.

Ми можемо приблизно приблизні

\[MC(x)=C′(x)=\lim_{h→0}\frac{C(x+h)−C(x)}{h} \nonumber \]

вибравши відповідне значення для$h$. Оскільки$x$ представляє об'єкти, розумним і малим значенням для$h$ є 1. Таким чином, підставивши$h=1$, отримуємо наближення$MC(x)=C′(x)≈C(x+1)−C(x)$. Отже,$C′(x)$ для даної вартості$x$ можна розглядати як зміну вартості, пов'язану з виробництвом однієї додаткової позиції. Аналогічним чином$MR(x)=R′(x)$ наближається дохід, отриманий від продажу однієї додаткової позиції, і$MP(x)=P′(x)$ наближається прибуток, отриманий при виробництві і продажу одного додаткового предмета.

Приклад$\PageIndex{6}$: Applying Marginal Revenue

Припустимо, що кількість вечерь з барбекю, які можна продати$x$, може бути пов'язана з ціною, що стягується$p$, за рівнянням$p(x)=9−0.03x,0≤x≤300$.

В цьому випадку дохід в доларах, отриманий при продажу обідів з$x$ барбекю, дає

$R(x)=xp(x)=x(9−0.03x)=−0.03x^2+9x\;\text{ for }0≤x≤300$.

Використовуйте функцію граничного доходу, щоб оцінити дохід, отриманий від продажу вечері з$101^{\text{st}}$ барбекю. Порівняйте це з фактичним доходом, отриманим від продажу цього обіду.

Рішення

Спочатку знайдіть функцію граничного доходу:$MR(x)=R′(x)=−0.06x+9.$

Далі використовуйте$R′(100)$ для наближення$R(101)−R(100)$, виручку, отриману від продажу$101^{\text{st}}$ обіду. Так як$R′(100)=3$, дохід, отриманий від продажу$101^{\text{st}}$ вечері, становить приблизно 3 долари.

Фактична виручка, отримана від продажу$101^{\text{st}}$ обіду, становить

$R(101)−R(100)=602.97−600=2.97,$або$$2.97.$

Маржинальний дохід є досить хорошою оцінкою в цьому випадку і має перевагу в тому, що його легко обчислити.

Вправа$\PageIndex{4}$

Припустимо, що прибуток, отриманий від продажу$x$ рибних вечерь, дає$P(x)=−0.03x^2+8x−50$. Використовуйте функцію граничного прибутку для оцінки прибутку від продажу обіду з$101^{\text{st}}$ риб'ячим смаженням.

Підказка: Використовуйте$P′(100)$ для наближення$P(101)−P(100)$.

Відповідь: $2

Ключові поняття

Використовуючи$f(a+h)≈f(a)+f′(a)h$, можна оцінити$f(a+h)$ дані$f′(a)$ і$f(a)$.
Швидкість зміни положення - швидкість, а швидкість зміни швидкості - прискорення. Швидкість - абсолютне значення, або величина швидкості.
Темпи приросту населення та теперішнє населення можуть бути використані для прогнозування чисельності майбутнього населення.
Функції граничних витрат, граничного доходу та граничного прибутку можуть бути використані для прогнозування, відповідно, витрат на виробництво ще одного предмета, доходу, отриманого від продажу ще одного предмета, і прибутку, отриманого шляхом виробництва та продажу ще одного предмета.

Глосарій

прискорення: це швидкість зміни швидкості, тобто похідна швидкості

сума змін: кількість функції$f(x)$ за інтервал$[x,x+h] is f(x+h)−f(x)$

середня швидкість зміни: є функцією$f(x)$ протягом інтервалу$[x,x+h]$$\frac{f(x+h)−f(a)}{b−a}$

гранична вартість: похідна від функції витрат, або приблизна вартість виробництва ще однієї позиції

граничний дохід: похідна від функції доходу, або приблизний дохід, отриманий від продажу ще одного предмета

граничний прибуток: похідна від функції прибутку, або приблизний прибуток, отриманий шляхом виробництва і продажу ще одного предмета

темпи приросту населення: є похідною від населення по відношенню до часу

швидкість: - абсолютне значення швидкості,$|v(t)|$ тобто швидкість об'єкта в час, швидкість$t$ якого задається$v(t)$

Приклад\(\PageIndex{1}\): Estimating the Value of a Function

Вправа\(\PageIndex{1}\)

Визначення

Приклад\(\PageIndex{2}\): Comparing Instantaneous Velocity and Average Velocity

Приклад\(\PageIndex{3}\): Interpreting the Relationship between \(v(t)\) and \(a(t)\)

Приклад\(\PageIndex{4}\): Position and Velocity

Вправа\(\PageIndex{2}\)

Визначення

Приклад\(\PageIndex{5}\): Estimating a Population

Вправа\(\PageIndex{3}\)

Визначення

Приклад\(\PageIndex{6}\): Applying Marginal Revenue

Вправа\(\PageIndex{4}\)