11.2: Обчислення та векторно-значні функції

Попередній розділ познайомив нас з новим математичним об'єктом, векторно-значною функцією. Тепер ми застосовуємо концепції числення до цих функцій. Ми починаємо з межі, потім пропрацюємо наш шлях через похідні до інтегралів.

Межі векторно-значних функцій

Початкове визначення межі векторно-значної функції трохи залякує, як і визначення межі у Визначенні 1. Теорема, що слідує за визначенням, показує, що на практиці приймати межі векторно-значних функцій не складніше, ніж брати межі дійсних функцій.

Визначення 68: Межі векторно-значних функцій

\(I\)Дозволяти бути відкритий інтервал\(c\), що містить, і нехай\(\vecs r(t)\) бути векторної функції, визначеної на\(I\), крім можливо в\(c\). Межа\(\vecs r(t)\), як\(t\) підходи\(c\)\(\vecs L\), виражається як

\[\lim_{t\to c} \vecs r(t) = \vecs L,\]

означає, що з огляду на будь-який\(\epsilon>0\), існує\(\delta>0\) таке, що для всіх\(t\neq c\), якщо\(|t-c| <\delta\), у нас є\(\norm{\vecs r(t) - \vecs L} < \epsilon.\)

Зверніть увагу, як вимірювання відстані між дійсними числами є абсолютним значенням їх різниці; мірою відстані між векторами є векторна норма, або величина, їх різниці.

Теорема 89: Межі векторно-значних функцій

1. \(\vecs r(t) = \langle \,f(t),g(t)\,\rangle\)Дозволяти векторно-значною функцією в\(\mathbb{R}^2\) визначеному на відкритому інтервалі,\(I\) що містить\(c\). Тоді\[\lim_{t\to c} \vecs r(t) = \langle \lim_{t\to c}f(t)\, , \,\lim_{t\to c} g(t)\rangle.\]
2. \(\vecs r(t) = \langle \,f(t),g(t),h(t)\,\rangle\)Дозволяти векторно-значною функцією в\(\mathbb{R}^3\) визначеному на відкритому інтервалі,\(I\) що містить\(c\). Тоді\[\lim_{t\to c} \vecs r(t) = \langle \lim_{t\to c}f(t)\, , \,\lim_{t\to c} g(t)\,, \,\lim_{t\to c} h(t)\rangle\]

Теорема 89 стверджує, що ми обчислюємо межі покомпонентно.

Приклад\(\PageIndex{1}\): Finding limits of vector-valued functions

Дозвольте\(\vecs r(t) = \langle \frac{\sin t}{t},\, t^2-3t+3,\,\cos t\rangle.\) знайти\( \lim_{t\to 0}\vecs r(t)\).

Рішення

Застосовуємо теорему і обчислюємо межі покомпонентно.

\ [\ почати {вирівнювати*}
\ lim_ {t\ to0}\ векс r (t) &=\ ланголь\ lim_ {t\ to 0}\ frac {\ sin t}\,\,\ lim_ {t\ to 0} t ^2-3t+3\,,\ lim_ {t\ to 0}\ cos t\ rangle\\
&=\ лангет 1,3,1\ коло.
\ end {вирівнювати*}\]

Безперервність

Визначення 69: Неперервність векторно-значних функцій

\(\vecs r(t)\)Дозволяти векторну функцію, визначену на відкритому інтервалі,\(I\) що містить\(c\).

1. \(\vecs r(t)\)є безперервним при\(c\) if\( \lim_{t\to c} \vecs r(t) = r(c)\).
2. Якщо\(\vecs r(t)\) є безперервним взагалі\(c\) в\(I\), то\(\vecs r(t)\) безперервно включений\(I\).

У нас знову є теорема, яка дозволяє нам оцінювати безперервність компонентно.

ТЕОРЕМА 90: Неперервність векторно-значних функцій

\(\vecs r(t)\)Дозволяти векторну функцію, визначену на відкритому інтервалі,\(I\) що містить\(c\). \(\vecs r(t)\)є безперервним при\(c\) якщо, і тільки якщо, кожна з його складових функцій є безперервною в\(c\).

Приклад\(\PageIndex{2}\): Evaluating continuity of vector-valued functions

Дозвольте\(\vecs r(t) = \langle \frac{\sin t}{t},\, t^2-3t+3,\,\cos t\rangle.\) Визначити\(\vecs r\), чи є безперервним в\(t=0\) і\(t=1\).

Рішення

У той час як друга і третя складові\(\vecs r(t)\) визначаються при\(t=0\), перший компонент,\((\sin t)/t\),, не є. Оскільки перший компонент навіть не визначається в\(t=0\), не\(\vecs r(t)\) визначається в\(t=0\), а отже, він не є безперервним при\(t=0\).

У\(t=1\) кожного з компонентів функції є безперервними. Тому\(\vecs r(t)\) є безперервним при\(t=1\).

похідні

Розглянемо векторно-значну функцію,\(\vecs r\) визначену на відкритому інтервалі,\(I\) що містить\(t_0\) і\(t_1\). Ми можемо обчислити зміщення\(\vecs r\) на\([t_0,t_1]\), як показано на малюнку\(\PageIndex{1a}\). Нагадаємо, що ділення вектора зміщення на\(t_1-t_0\) дає середню швидкість зміни на\([t_0,t_1]\), як показано в\(\PageIndex{1b}\).

Малюнок\(\PageIndex{1}\): Ілюстрація зміщення, що призводить до розуміння похідної векторно-значних функцій.

Похідна векторно-значної функції - це міра миттєвої швидкості зміни, виміряна, приймаючи межу, оскільки довжина\([t_0,t_1]\) переходить до 0. Замість того, щоб думати про інтервал як\([t_0,t_1]\), ми думаємо про це як\([c,c+h]\) для деякого значення\(h\) (отже, інтервал має довжину\(h\)). Середня швидкість зміни становить

\[\frac{\vecs r(c+h)-\vecs r(c)}{h}\]

за будь-яке значення\(h\neq0\). Ми беремо межу,\(h\to0\) щоб виміряти миттєву швидкість зміни; це похідна від\(\vecs r\).

Означення 70: Похідна векторно-значної функції

\(\vecs r(t)\)Дозволяти бути безперервним на відкритому інтервалі\(I\), що містить\(c\).

1. Похідне від\(\vecs r\) at\(t=c\) є\[\vecs r ^\prime (c) = \lim_{h\to 0} \frac{\vecs r(c+h) - \vecs r(c)}{h}.\]
2. Похідне від\(\vecs r\) є\[\vecs r ^\prime (t) = \lim_{h\to 0} \frac{\vecs r(t+h) - \vecs r(t)}{h}.\]

Примітка: Альтернативні позначення для похідної від\(\vecs r\) включають:\[\vecs r ^\prime(t) = \frac{d}{dt}\big(\,\vecs r(t)\,\big) = \frac{d\vecs r}{dt}.\]

Якщо векторно-значна функція має похідну для всіх\(c\) у відкритому інтервалі\(I\), ми говоримо,\(\vecs r(t)\) що диференційовна на\(I\).

Ще раз ми можемо розглядати це визначення як страхітливе, але нагадаємо, що ми можемо оцінювати межі компонентно. Наступна теорема підтверджує, що це означає, що ми можемо обчислити похідні покомпонентно, роблячи завдання не надто складним.

Теорема 91: Похідні векторно-значних функцій

1. Нехай\(\vecs r(t) = \langle \, f(t), g(t)\,\rangle\). Тоді\[\vecs r ^\prime(t) = \langle\, f^\prime (t), g^\prime (t)\, \rangle.\]
2. Нехай\(\vecs r(t) = \langle \, f(t), g(t), h(t)\,\rangle\). Тоді\[\vecs r ^\prime(t) = \langle\, f^\prime (t), g^\prime (t), h^\prime (t)\, \rangle.\]

Приклад\(\PageIndex{3}\): Derivatives of vector-valued functions

Нехай\(\vecs r(t) = \langle t^2,t\rangle\).

1. Ескіз\(\vecs r(t)\) і\(\vecs r ^\prime(t)\) на однакових осях.
2. Обчислити\(\vecs r ^\prime(1)\) і намалювати цей вектор з його початковою точкою в початку і в\(\vecs r(1)\).

Рішення

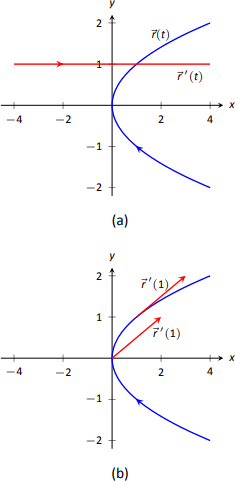
1. Теорема 91 дозволяє обчислити похідні покомпонентно, так\[\vecs r ^\prime(t) = \langle 2t, 1\rangle.\]\(\vecs r(t)\) і\(\vecs r ^\prime(t)\) графуються разом на малюнку 11.9 (a). Зверніть увагу, як побудова двох з них разом, таким чином, не дуже освітлює. При роботі з реальними функціями, побудова графіка\(f(x)\) з\(f^\prime (x)\) дала нам корисну інформацію, оскільки ми змогли порівняти\(f\) і\(f^\prime \) при тих же\(x\) -значеннях. При роботі з векторно-значними функціями важко сказати, які точки на графіку\(\vecs r ^\prime\) відповідають яким точкам на графіку\(\vecs r\).
   
2. Ми легко обчислюємо\(\vecs r ^\prime(1) = \langle 2,1\rangle\), який намальований на малюнку\(\PageIndex{2a}\) з його початковою точкою в початку, а також на\(\vecs r(1) = \langle 1,1\rangle.\) Ці накидані на малюнку\(\PageIndex{2b}\).

Рисунок\(\PageIndex{2}\): Графік похідної векторно-значної функції у прикладі 11.2.3

Приклад\(\PageIndex{4}\): Derivatives of vector-valued functions

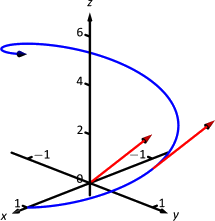
Нехай\(\vecs r(t) = \langle \cos t, \sin t, t\rangle\). Обчислити\(\vecs r ^\prime(t)\) і\(\vecs r ^\prime(\pi/2)\). \(\vecs r ^\prime(\pi/2)\)Ескіз з його початковою точкою на початку і в\(\vecs r(\pi/2)\).

Рішення

Обчислюємо\(\vecs r ^\prime\) як\(\vecs r ^\prime(t) = \langle -\sin t, \cos t, 1\rangle\). На\(t= \pi/2\), у нас є\(\vecs r ^\prime(\pi/2) = \langle -1,0,1\rangle\). На малюнку\(\PageIndex{3}\) зображений графік\(\vecs r(t)\), з\(\vecs r ^\prime(\pi/2)\) нанесеною його початковою точкою в початку і в\(\vecs r(\pi/2)\).

Рисунок\(\PageIndex{3}\): Перегляд векторної функції та її похідної в одній точці.

У Прикладах\(\PageIndex{3}\) і\(\PageIndex{4}\), замальовуючи певну похідну з її початковою точкою на початку, здається, не виявили нічого істотного. Однак, коли ми намалювали вектор з його початковою точкою на відповідній точці на графіку, ми побачили щось значне: вектор виявився дотичним до графіка. Ми ще не визначили, що означає «тангенс» з точки зору кривих у просторі; насправді ми використовуємо похідну для визначення цього терміна.

Визначення 71: Дотичний вектор, Дотична лінія

\(\vecs r(t)\)Дозволяти диференційовну векторно-значну функцію на відкритому інтервалі\(c\),\(I\) що містить, де\(\vecs r ^\prime(c)\neq \vecs 0\).

1. Вектор\(\vecs v\) є дотичною до графа\(\vecs r(t)\) at\(t=c\)\(\vecs v\) if паралельно\(\vecs r ^\prime(c)\).
2. Дотична пряма} до графіка\(\vecs r(t)\) at\(t=c\) - це пряма, що проходить\(\vecs r(c)\) з напрямком, паралельним\(\vecs r ^\prime(c)\). Рівняння дотичної прямої
   \[\vecs \ell(t) = \vecs r(c) + t\,\vecs r ^\prime(c).\]

Приклад\(\PageIndex{5}\): Finding tangent lines to curves in space

Нехай\(\vecs r(t) = \langle t,t^2,t^3\rangle\) далі\([-1.5,1.5]\). Знайти векторне рівняння прямої дотичної до графа\(\vecs r\) at\(t=-1\).

Рішення

Щоб знайти рівняння прямої, нам потрібна точка на прямій і напрямок лінії. Крапку задають\(\vecs r(-1) = \langle -1,1,-1\rangle\). (Щоб було зрозуміло,\(\langle -1,1,-1\rangle\) це вектор, а не точка, але ми використовуємо точку, «на яку вказує» цим вектором.)

Напрямок походить від\(\vecs r ^\prime(-1)\). Ми обчислюємо, компонентно,\(\vecs r ^\prime(t) = \langle 1,2t, 3t^2\rangle\). Таким чином\(\vecs r ^\prime(-1) = \langle 1,-2,3\rangle\).

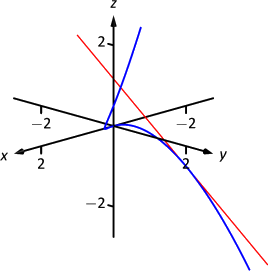
Векторне рівняння прямої є\(\ell(t) = \langle -1,1,-1\rangle + t\langle 1,-2,3\rangle\). Ця лінія і\(\vecs r(t)\) намальовані, з двох точок зору, на малюнку\(\PageIndex{4a}\) і\(\PageIndex{4b}\).

Малюнок\(\PageIndex{4}\): Графік кривої в просторі з її дотичною лінією.

Приклад\(\PageIndex{6}\): Finding tangent lines to curves

Знайти рівняння ліній, дотичних до\(\vecs r(t) = \langle t^3,t^2\rangle\) at\(t=-1\) і\(t=0\).

Рішення

Ми знаходимо це\(\vecs r ^\prime(t) = \langle 3t^2,2t\rangle\). На\(t=-1\), у нас є

\[\vecs r(-1) = \langle -1,1\rangle\quad \text{and}\quad \vecs r ^\prime(-1) = \langle 3,-2\rangle, \nonumber\]

тому рівняння прямої дотичної до графіка\(\vecs r(t)\) at\(t=-1\) дорівнює

\[\ell(t) = \langle -1,1\rangle + t\langle 3,-2\rangle. \nonumber\]

Цей рядок зображений на\(\vecs r(t)\) малюнку\(\PageIndex{5}\).

Малюнок\(\PageIndex{5}\): Графік\(\vecs{r}(t)\) та його дотична лінія у прикладі\(\PageIndex{6}\).

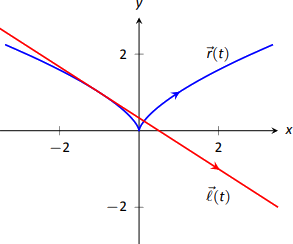
На\(t=0\), у нас є\(\vecs r ^\prime(0) = \langle 0,0\rangle=\vecs 0\)! Це означає, що дотична лінія «не має напрямку». Ми не можемо застосувати Визначення 71, отже, не можемо знайти рівняння дотичної лінії.

Ми не змогли обчислити рівняння дотичної лінії до\(\vecs r(t)= \langle t^3,t^2\rangle\) at,\(t=0\) тому що\(\vecs r ^\prime(0) = \vecs 0\). Графік на малюнку 11.12 показує, що в цій точці є розрив. Це призводить нас до іншого визначення гладкого, раніше визначеного Визначенням 46 у розділі 9.2.

Визначення 72: Гладкі векторні функції

\(\vecs r(t)\)Дозволяти диференційовну векторно-значну функцію на відкритому інтервалі\(I\). \(\vecs r(t)\)є гладким,\(I\) якщо\(\vecs r ^\prime(t)\neq \vecs 0\) на\(I\).

Встановлюючи похідні векторно-значних функцій, ми зараз досліджуємо зв'язки між похідною та іншими векторними операціями. Наступна теорема стверджує, як похідна взаємодіє з векторним додаванням та різними векторними добутками.

ТЕОРЕМА 92: Властивості похідних векторно-значних функцій

\(\vecs r\)\(\vecs s\)Дозволяти і бути диференційованими векторно-значними функціями,\(f\) нехай диференційовна дійсна функція, і нехай\(c\) бути дійсним числом.

1. \( \frac{d}{dt}\Big(\vecs r(t) \pm \vecs s(t)\Big) = \vecs r ^\prime(t) \pm \vecs s\,'(t)\)
2. \( \frac{d}{dt}\Big(c\vecs r(t)\Big) = c\vecs r ^\prime(t)\)
3. \(\frac{d}{dt}\Big(f(t)\vecs r(t)\Big) = f^\prime (t)\vecs r(t) + f(t)\vecs r ^\prime(t)\)Правило продукту
4. \(\frac{d}{dt}\Big(\vecs r(t)\cdot \vecs s(t) \Big) = \vecs r ^\prime(t)\cdot \vecs s(t) + \vecs r(t)\cdot \vecs s\,'(t)\)Правило продукту
5. \(\frac{d}{dt}\Big(\vecs r(t)\times \vecs s(t) \Big) = \vecs r ^\prime(t)\times \vecs s(t) + \vecs r(t)\times \vecs s\,'(t)\)Правило продукту
6. \(\frac{d}{dt}\Big(\vecs r\big(f(t)\big)\Big) = \vecs r ^\prime\big(f(t)\big)f^\prime (t)\)Правило ланцюга

Приклад\(\PageIndex{7}\): Using derivative properties of vector-valued functions

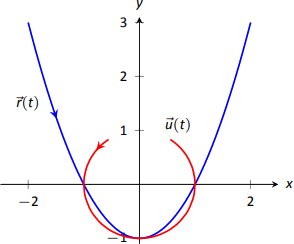
Дозволяти\(\vecs r(t) = \langle t, t^2-1\rangle\) і нехай\(\vecs u(t)\) бути блок вектор, який вказує в напрямку\(\vecs r(t)\).

1. Графік\(\vecs r(t)\) і\(\vecs u(t)\) на тих же осях, на\([-2,2]\).
2. Знайдіть\(\vecs u\,'(t)\) і\(\vecs u\,'(-2)\) накидайте,\(\vecs u\,'(-1)\) і\(\vecs u\,'(0)\). Намалюйте кожну з початковою точкою відповідної точки на графіку\(\vecs u\).

Рішення

1. Щоб сформувати одиничний вектор, який вказує в напрямку\(\vecs r\), нам потрібно розділити\(\vecs r(t)\) на його величину.
   \[\norm{\vecs r(t)} = \sqrt{t^2+(t^2-1)^2} \quad \Rightarrow \quad \vecs u(t) = \frac{1}{\sqrt{t^2+(t^2-1)^2}}\langle t,t^2-1\rangle.\]
   \(\vecs r(t)\)і\(\vecs u(t)\) зображені на малюнку 11.13. Зверніть увагу, як графік\(\vecs u(t)\) утворює частину кола; це має бути так, як довжина\(\vecs u(t)\) дорівнює 1 для всіх\(t\).
   
2. Для обчислення\(\vecs u\,'(t)\) ми використовуємо теорему 92, написання\[\vecs u(t) = f(t)\vecs r(t),\quad \text{where}\quad f(t) = \frac{1}{\sqrt{t^2+(t^2-1)^2}}=\big(t^2+(t^2-1)^2\big)^{-1/2}.\]
   (Ми могли б написати,\[\vecs u(t) = \langle \frac{t}{\sqrt{t^2+(t^2-1)^2}}, \frac{t^2-1}{\sqrt{t^2+(t^2-1)^2}}\rangle\]
   а потім взяти похідну. Це питання переваги; цей останній метод вимагає двох застосувань правила частки, де наш метод використовує правила продукту та ланцюга.)
   
   Ми знаходимо,\(f^\prime (t)\) використовуючи правило ланцюга: Тепер\[\begin{align*}f^\prime (t) &= -\frac12\big(t^2+(t^2-1)^2\big)^{-3/2}\big(2t+2(t^2-1)(2t)\big)\\&= -\frac{2t(2t^2-1)}{2\big(\sqrt{t^2+(t^2-1)^2}\,\big)^3}\end{align*}\]
   
   ми знаходимо,\(\vecs u\,'(t)\) використовуючи частину 3 Теореми 92:\[\begin{align*}\vecs u\,'(t) &= f^\prime (t)\vecs u(t) + f(t)\vecs u\,'(t) \\&= -\frac{2t(2t^2-1)}{2\big(\sqrt{t^2+(t^2-1)^2}\,\big)^3}\langle t,t^2-1\rangle + \frac{1}{\sqrt{t^2+(t^2-1)^2}}\langle 1,2t\rangle.\end{align*}\]
   
   Це, безумовно, дуже «безладно;» таке зазвичай буває, коли ми маємо справу з одиничними векторами. Ми можемо використовувати цю формулу для обчислення\(\vecs u\,(-2)\),\(\vecs u\,(-1)\) і\(\vecs u\,(0)\):\[\begin{align*}\vecs u\,(-2) &= \langle -\frac{15}{13 \sqrt{13}},-\frac{10}{13\sqrt{13}}\rangle \approx \langle -0.320,-0.213\rangle\\\vecs u\,(-1) &= \langle 0,-2\rangle\\\vecs u\,(0) &= \langle 1,0\rangle\end{align*}\]

Малюнок\(\PageIndex{6}\): Графік\(\vecs{r}(t)\text{ and } \vecs{u}(t)\) у прикладі\(\PageIndex{7}\)

Кожен з них намальований на малюнку\(\PageIndex{6}\). Зверніть увагу, як довжина вектора дає вказівку на те, наскільки швидко коло простежується в цій точці. Коли\(t=-2\) коло малюється відносно повільно; коли\(t=-1\) коло простежується набагато швидше.

Основним геометричним фактом є те, що пряма, дотична до кола в точці\(P\), перпендикулярна лінії, що проходить через центр кола і\(P\). Це проілюстровано на малюнку 11.14; кожен дотичний вектор перпендикулярний лінії, яка проходить через її початкову точку і центр кола. Оскільки центр кола є початком, ми можемо констатувати це іншим способом:\(\vecs u\,'(t)\) є ортогональним до\(\vecs u(t)\).

Нагадаємо, що точковий добуток служить тестом на ортогональність: якщо\(\vecs u\cdot \vecs v = 0\),\(\vecs u\) то ортогонально до\(\vecs v\). Таким чином, у наведеному вище прикладі,\(\vecs u(t)\cdot \vecs u\,'(t)=0\).

Це справедливо для будь-якої векторної функції, яка має постійну довжину, тобто, що простежує частину кола. Пізніше це має важливі наслідки, тому ми висловлюємо це як теорему (і залишаємо її формальний доказ як вправу.)

ТЕОРЕМА 93 Векторно-значні функції постійної довжини

\(\vecs r(t)\)Дозволяти диференційовну векторно-значну функцію на відкритому інтервалі\(I\) постійної довжини. Тобто,\(\norm{\vecs r(t)} = c\) для всіх\(t\) в\(I\) (еквівалентно,\(\vecs r(t)\cdot \vecs r(t) = c^2\) для всіх\(t\) в\(I\)). Тоді\(\vecs r(t)\cdot\vecs r ^\prime(t) = 0\) для всіх\(t\) в\(I\).

Інтеграція

Також покомпонентно оцінюються невизначені та визначені інтеграли векторно-значних функцій.

ТЕОРЕМА 94: Невизначені та визначені інтеграли векторно-значних функцій

\(\vecs r(t) = \langle f(t),g(t)\rangle\)Дозволяти бути векторно-значною функцією в\(\mathbb{R}^2\).

1. \( \int \vecs r(t)\ dt = \langle \int f(t)\ dt, \int g(t)\ dt\rangle\)
2. \( \int_a^b \vecs r(t)\ dt = \langle \int_a^b f(t)\ dt, \int_a^b g(t)\ dt\rangle\)

Аналогічний оператор тримає для векторно-значних функцій в\(\mathbb{R}^3\).

Приклад\(\PageIndex{8}\): Evaluating a definite integral of a vector-valued function

Нехай\(\vecs r(t) = \langle e^{2t},\sin t\rangle\). Оцінити\( \int_0^1 \vecs r(t) \ dt\).

Рішення

Ми слідуємо теоремі 94.

\ [\ begin {align*}
\ int_0^1\ vecs r (t)\ dt &=\ int_0^1\ лангове e^ {2t},\ sin t\ діапазон\ dt\\
&=\ лангле\ int_0^1 e^ {2t}\ dt\,\ int_0^1\ sin t\ dt\ rangle\\
&=\ lкут frac12e^ {2t}\ Великий|_0^1\, -\ cos t\ Big|_0^1\ діапазон\\
&=\ ланголь\ розрив 12 (e^2-1)\, -\ cos (1) +1\ діапазон\\
&\ приблизно\ кут 3.19,0.460\ діапазон.
\ end {вирівнювати*}\]

Приклад\(\PageIndex{9}\): Solving an initial value problem

Нехай\(\vecs r ^{\prime\prime}(t) = \langle 2, \cos t, 12t\rangle\). Знайти\(\vecs r(t)\) де:

1. \(\vecs r(0) = \langle -7,-1,2\rangle\)і
2. \(\vecs r ^\prime(0) = \langle 5,3,0\rangle.\)

Рішення

Знаючи\(\vecs r ^{\prime\prime}(t) = \langle 2,\cos t, 12t\rangle\), знаходимо,\(\vecs r ^\prime(t)\) оцінюючи невизначений інтеграл.

\ [\ begin {align*}
\ int\ vecs r ^ {\ прайм\ прайм} (t) DT &=\ ланголь\ int 2 dt\,\ int\ cos t dt\,\ int 12t dt\ діапазон\\
&=\ лангл 2t+C_1,\ sin t+ C_2, 6t^2 + C_3\ діапазон\\
&=\ lкут 2t,\ sin t,6t ^ 2\ діапазон +\ кут C_1, C_2, C_3\ діапазон\\
&= \ кут 2t,\ sin t,6t^2\ діапазон +\ вектор C_1.
\ end {вирівнювати*}\]

Зверніть увагу, як кожен невизначений інтеграл створює власну константу, яку ми збираємо як один константний вектор\(\vecs C_1\). Знання\(\vecs r ^\prime(0) = \langle 5,3,0\rangle\) дозволяє нам вирішувати для\(\vecs C_1\):

\ [\ begin {align*}
\ vecs r ^\ прайм (t) & =\ ланголь 2t,\ sin t,6t^2\ діапазон +\ vecs C_1
\\ vecs r ^\ прайм (0) &=\ кут 0,0,0\ діапазон +\ vecs C_1
\\\ лангл 5,3,0\ діапазон &=\ vecs C_1.
\ end {вирівнювати*}\]

Отже\(\vecs r ^\prime(t) = \langle 2t,\sin t,6t^2\rangle + \langle 5,3,0\rangle = \langle 2t+5, \sin t + 3, 6t^2\rangle\). Щоб знайти\(\vecs r(t)\), ми інтегруємо ще раз.

\ [\ почати {вирівнювати*}
\ int\ vecs r ^\ прайм (t)\ dt &=\ ланкут\ int 2t+5\ dt,\ int\ sin t + 3\ dt,\ int 6t^2 dt\ діапазон\\
&=\ кут t^2+5t, -\ cos t + 3t, 2t^3\ діапазон +\ vecs C_2.
\ end {вирівнювати*}\]

З\(\vecs r(0) = \langle -7,-1,2\rangle\), ми вирішуємо для\(\vecs C_2\):

\ [\ begin {align*}
\ vecs r (t) &=\ ланкут t^2+5t, -\ cos t + 3t, 2t^3\ діапазон +\ vecs C_2
\\\ vecs r (0) &=\ лангл 0, -1,0\ діапазон +\ vecs C_2\
\\ langle -7, -1,0\ 2\ діапазон &=\ кут 0, -1,0\ діапазон +\ vecs C_2
\\\ кут -7,0,2\ діапазон &=\ вектор C_2.
\ end {вирівнювати*}\]

Так\(\vecs r(t) = \langle t^2+5t, -\cos t + 3t, 2t^3\rangle + \langle -7,0,2\rangle = \langle t^2+5t-7,-\cos t+3t,2t^3+2\rangle.\)

Що означає інтеграція векторно-значної функції? Існує багато застосувань, але жоден такий прямий, як «область під кривою», яку ми використовували для розуміння інтеграла реальної функції.

Ключове розуміння для нас походить від розгляду інтеграла похідної:\[\int_a^b \vecs r ^\prime(t) dt = \vecs r(t)\Big|_a^b = \vecs r(b)-\vecs r(a).\]
Інтеграція функції швидкості зміни дає зміщення.

Відзначаючи, що векторно-значні функції тісно пов'язані з параметричними рівняннями, можна описати довжину дуги графа векторно-значної функції як інтеграл. За заданими\(x=f(t)\)\(y=g(t)\) параметричними рівняннями довжина\([a,b]\) дуги на графіку дорівнює

\[\text{Arc Length} = \int_a^b\sqrt{f^\prime (t)^2+g^\prime (t)^2} dt,\]

як зазначено в теоремі 82 в розділі 9.3. Якщо\(\vecs r (t) = \langle f(t), g(t)\rangle\), зверніть увагу, що\(\sqrt{f^\prime (t)^2+g^\prime (t)^2} = \norm{\vecs r ^\prime(t)}\). Тому ми можемо висловити довжину дуги графа векторно-значної функції як інтеграл величини її похідної.

ТЕОРЕМА 95: Довжина дуги векторно-значної функції

\(\vecs r (t)\)Дозволяти бути векторно-значною функцією, де\(\vecs r ^\prime(t)\) є безперервним на\([a,b]\). Довжина\(L\) дуги графа\(\vecs r (t)\) дорівнює\[L = \int_a^b \norm{\vecs r ^\prime(t)}\ dt.\]

Зауважте, що ми насправді інтегруємо скалярну функцію тут, а не векторну функцію.

Наступний розділ приймає те, що ми встановили до цього часу, і застосовує його до об'єктів, що знаходяться в русі. Ми дозволимо\(\vecs r (t)\) описати шлях об'єкта в площині або в просторі і відкриємо інформацію, надану\(\vecs r ^\prime(t)\) і\(\vecs r ^{\prime\prime}(t)\).