Skip to main content
LibreTexts - Ukrayinska

3.2: Вектори

  1. Last updated
  2. Save as PDF
  • Page ID
    75095

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Компоненти вектора

    Вектори - це геометричні зображення величини і напрямку і можуть бути виражені у вигляді стрілок в двох або трьох вимірах.

    цілі навчання

    • Контраст двовимірних і тривимірних векторів

    Вектори - це геометричні зображення величини і напрямку, які часто представлені прямими стрілками, починаючи з однієї точки на осі координат і закінчуючи в іншій точці. Всі вектори мають довжину, звану величиною, яка представляє деяку цікаву якість, щоб вектор можна було порівняти з іншим вектором. Вектори, будучи стрілками, також мають напрямок. Це відрізняє їх від скалярів, які є простими числами без напрямку.

    Вектор визначається його величиною та орієнтацією щодо набору координат. Це часто корисно при аналізі векторів, щоб розбити їх на складові частини. Для двовимірних векторів цими складовими є горизонтальні і вертикальні. Для тривимірних векторів величина складова однакова, але складова напрямку виражається через xx, yy і zz.

    Розкладання вектора

    Щоб візуалізувати процес розкладання вектора на його складові, почніть з малювання вектора від початку набору координат. Далі проведіть пряму лінію від початку вздовж осі x, поки лінія не буде рівною з кінчиком вихідного вектора. Це горизонтальна складова вектора. Щоб знайти вертикальну складову, проведіть лінію прямо вгору від кінця горизонтального вектора, поки не досягнете кінчика вихідного вектора. Ви повинні знайти у вас прямокутний трикутник такий, що початковим вектором є гіпотенуза.

    Розкладання вектора на горизонтальні та вертикальні компоненти є дуже корисною технікою в розумінні проблем фізики. Всякий раз, коли ви бачите рух під кутом, ви повинні думати про це як про переміщення горизонтально і вертикально одночасно. Спрощення векторів таким чином може прискорити обчислення і допомогти відстежувати рух об'єктів.

    Скаляри та вектори: пан Андерсен пояснює відмінності між скалярними та векторними величинами. Він також використовує демонстрацію, щоб показати важливість векторів та додавання векторів.

    зображення

    Компоненти вектора: вихідний вектор, визначений відносно набору осей. Горизонтальна складова тягнеться від початку вектора до його найдальшої координати x. Вертикальна складова тягнеться від осі x до самої вертикальної точки вектора. Разом дві складові та вектор утворюють прямокутний трикутник.

    Скаляри проти векторів

    Скаляри - це фізичні величини, представлені одним числом, а вектори представлені як числом, так і напрямком.

    цілі навчання

    • Розрізняють різницю між величинами, скалярами і векторами представляють

    Фізичні величини зазвичай можна розмістити на дві категорії, вектори та скаляри. Ці дві категорії типізуються тим, яку інформацію вони вимагають. Вектори вимагають двох частин інформації: величини і напрямку. На відміну від цього, скаляри вимагають тільки величини. Скаляри можна розглядати як числа, тоді як вектори повинні розглядатися більше як стрілки, що вказують у певному напрямку.

    зображення

    Вектор: приклад вектора. Вектори зазвичай представлені стрілками, довжина яких представляє величину і їх напрямок представлений напрямком стрілки.

    Вектори вимагають як величини, так і напрямку. Величина вектора - це число для порівняння одного вектора з іншим. У геометричній інтерпретації вектора вектор представлений стрілкою. Стрілка має дві частини, які визначають її. Дві частини - це його довжина, яка представляє величину та її напрямок щодо деякого набору осей координат. Чим більше величина, тим довше стрілка. Фізичні поняття, такі як зміщення, швидкість і прискорення - все це приклади величин, які можуть бути представлені векторами. Кожна з цих величин має як величину (наскільки далеко або як швидко), так і напрямок. Для того щоб вказати напрямок, має бути щось, до якого напрямок відносне. Зазвичай ця точка відліку являє собою набір координатних осей, таких як площина xy.

    Скаляри відрізняються від векторів тим, що не мають спрямованості. Скаляри використовуються в першу чергу для представлення фізичних величин, для яких напрямок не має сенсу. Деякі приклади таких: маса, висота, довжина, об'єм та площа. Розмова про напрямок цих величин не має сенсу і тому їх не можна виражати як вектори.

    Різниця між векторами та скалярами, вступ та основи: У цьому відео представлена різниця між скалярами та векторами. Введено уявлення про величину та напрямок та наведено приклади векторів та скалярів.

    Додавання та віднімання векторів графічно

    Вектори можна додавати або віднімати графічно, прокладаючи їх кінець до кінця на наборі осей.

    цілі навчання

    • Розрізняють різницю між величинами, скалярами і векторами представляють

    Додавання та віднімання векторів

    Одним із способів представлення фізичних величин як векторів полегшує аналіз, є легкість, з якою вектори можуть бути додані один до одного. Оскільки вектори є графічними візуалізаціями, додавання і віднімання векторів може здійснюватися графічно.

    Графічний метод векторного додавання також відомий як метод «голова до хвоста». Для початку намалюйте набір координатних осей. Далі намалюйте перший вектор своїм хвостом (підставою) біля початку координатних осей. Для векторного додавання не має значення, який вектор ви малюєте першим, оскільки додавання є комутаційним, але для віднімання переконайтеся, що вектор, який ви малюєте першим, є тим, з якого ви віднімаєте. Наступний крок - взяти наступний вектор і намалювати його таким чином, щоб його хвіст починався з голови попереднього вектора (сторона стрілки). Продовжуйте розміщувати кожен вектор на чолі попереднього, поки всі вектори, які ви хочете додати, не будуть об'єднані разом. Нарешті, проведіть пряму лінію від початку до голови кінцевого вектора в ланцюжку. Цей новий рядок є векторним результатом додавання цих векторів разом.

    зображення

    Графічне додавання векторів: Метод додавання векторів «голова до хвоста» вимагає, щоб ви розкладали перший вектор вздовж набору осей координат. Далі розташуйте хвіст наступного вектора на голові першого. Намалюйте новий вектор від початку до голови останнього вектора. Цей новий вектор є сумою вихідних двох.

    Векторне додавання Урок 1 з 2: Метод додавання голови до хвоста: Це відео дозволяє глядачам почати з векторного додавання та віднімання. Перший урок показує графічне додавання, а друге відео має більш математичний підхід і показує векторне додавання компонентів.

    Для віднімання векторів метод аналогічний. Переконайтеся, що перший вектор, який ви малюєте, - це той, з якого потрібно відняти. Потім, щоб відняти вектор, продовжуйте так, ніби додаючи протилежний цьому вектору. Іншими словами, переверніть вектор, який потрібно відняти по осях, а потім з'єднайте його хвіст до голови, ніби додаючи. Щоб перевернути вектор, просто покладіть його голову там, де був хвіст, і хвіст там, де була його голова.

    Додавання та віднімання векторів за допомогою компонентів

    Часто простіше додавати або віднімати вектори, використовуючи їх компоненти.

    цілі навчання

    • Продемонструйте, як додавати та віднімати вектори за компонентами

    Використання компонентів для додавання та віднімання векторів

    Іншим способом додавання векторів є додавання компонентів. Раніше ми бачили, що вектори можуть бути виражені через їх горизонтальну і вертикальну складові. Щоб додати вектори, просто висловіть обидва з точки зору їх горизонтальної та вертикальної складових, а потім додайте компоненти разом.

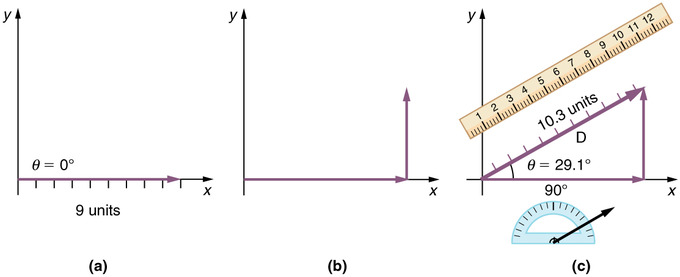
    зображення

    Вектор з горизонтальними та вертикальними компонентами: Вектор на цьому зображенні має величину 10,3 одиниці та напрямок 29,1 градуса над віссю x. Його можна розкласти на горизонтальну частину і вертикальну частину, як показано на малюнку.

    Наприклад, вектор довжиною 5 під кутом 36,9 градусів до горизонтальної осі матиме горизонтальну складову в 4 одиниці і вертикальну складову в 3 одиниці. Якби ми додали це до іншого вектора тієї ж величини і напрямку, ми б отримали вектор вдвічі довший під тим же кутом. Це можна побачити, додавши горизонтальні компоненти двох векторів\(\mathrm{(4+4)}\) та двох вертикальних компонентів (\(\mathrm{3+3}\)). Ці доповнення дають новий вектор з горизонтальною складовою\(\mathrm{8(4+4)}\) і вертикальною складовою\(\mathrm{6(3+3)}\). Щоб знайти результуючий вектор, просто помістіть хвіст вертикальної складової на голові (сторона стрілки) горизонтальної складової, а потім проведіть лінію від початку до голови вертикальної складової. Цей новий рядок є результуючим вектором. Він повинен бути в два рази довше оригіналу, так як обидва його складових в два рази більше, ніж були раніше.

    Щоб відняти вектори за складовими, просто відніміть дві горизонтальні компоненти один від одного і зробіть те ж саме для вертикальних компонентів. Потім намалюйте результуючий вектор, як ви це робили в попередній частині.

    Урок додавання векторів 2 з 2: Як додати вектори за компонентами: Це відео дозволяє глядачам почати додавання векторів за допомогою математичного підходу та показує додавання векторів за компонентами.

    Множення векторів на скаляр

    Множення вектора на скаляр змінює величину вектора, але не напрямок.

    цілі навчання

    • Узагальнити взаємодію між векторами та скалярами

    Огляд

    Хоча вектори і скаляри представляють різні типи фізичних величин, іноді їм необхідно взаємодіяти. Хоча додавання скаляра до вектора неможливо через їх різні розміри в просторі, можна помножити вектор на скаляр. Скаляр, однак, не можна помножити на вектор.

    Щоб помножити вектор на скаляр, просто помножте аналогічні складові, тобто величину вектора на величину скаляра. Це призведе до створення нового вектора з тим самим напрямком, але добуток двох величин.

    Приклад\(\PageIndex{1}\):

    Наприклад, якщо у вас є вектор A з певною величиною і напрямком, множення його на скаляр a з величиною 0,5 дасть новий вектор з величиною в половину оригіналу. Аналогічно, якщо взяти число 3, яке є чистим і безодиничним скаляром і помножити його на вектор, ви отримаєте версію вихідного вектора, яка в 3 рази довша. Як більш фізичний приклад візьмемо гравітаційну силу на об'єкт. Сила - це вектор з його величиною в залежності від скаляра, відомого як маса, і його напрямок вниз. Якщо маса об'єкта подвоюється, сила тяжіння також збільшується вдвічі.

    Множення векторів скалярами дуже корисно у фізиці. Більшість одиниць, що використовуються в векторних величинях, є іскрово скалярами, помноженими на вектор. Наприклад, одиниця метрів в секунду, що використовується в швидкості, яка є вектором, складається з двох скалярів, які є величинами: скаляром довжини в метрах і скаляром часу в секундах. Для того, щоб зробити це перетворення від величин до швидкості, потрібно помножити вектор одиниці в певному напрямку на ці скаляри.

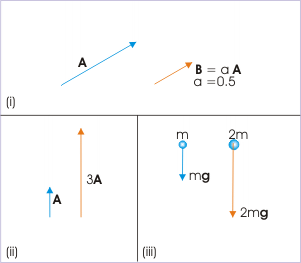
    зображення

    Скалярне множення: (i) Множення вектора\(\mathrm{A}\) на скаляр\(\mathrm{a=0.5}\) дає вектор\(\mathrm{B}\), який вдвічі менше. (ii) Множення вектора\(\mathrm{A}\) на 3 втричі збільшує його довжину. (iii) Подвоєння маси (скалярна) подвоює силу (вектор) сили тяжіння.

    Одиничні вектори та множення на скаляр

    Множення вектора на скаляр - це те саме, що і множення його величини на число.

    цілі навчання

    • Передбачити вплив множення вектора на скаляр

    Крім додавання векторів, вектори також можна помножити на константи, відомі як скаляри. Скаляри відрізняються від векторів тим, що вони представлені величиною, але не напрямком. Приклади скалярів включають масу, висоту або об'єм об'єкта.

    зображення

    Скалярне множення: (i) Множення вектора\(\mathrm{A}\) на скаляр\(\mathrm{a=0.5}\) дає вектор\(\mathrm{B}\), який вдвічі менше. (ii) Множення вектора\(\mathrm{A}\) на 3 втричі збільшує його довжину. (iii) Подвоєння маси (скалярна) подвоює силу (вектор) сили тяжіння.

    При множенні вектора на скаляр напрямок вектора незмінно і величина множиться на величину скаляра. Це призводить до появи нової векторної стрілки, спрямованої в тому ж напрямку, що і стара, але з більшою або меншою довжиною. Ви також можете виконати скалярне множення за допомогою компонентів вектора. Коли у вас є компоненти вектора, помножте кожен з компонентів на скаляр, щоб отримати нові компоненти і, отже, новий вектор.

    Корисним поняттям при вивченні векторів і геометрії є поняття одиничного вектора. Одиничний вектор - це вектор з довжиною або величиною одиниці. Вектори одиниць різні для різних координат. У декартових координатах напрямки x і y зазвичай позначаються\(\mathrm{\hat{x}}\) і\(\mathrm{\hat{y}}\). З трикутником над буквами називають «капелюх». Одиничні вектори в декартових координатах описують коло, відоме як «одиничне коло», яке має радіус один. У цьому можна переконатися, взявши всі можливі вектори довжини по одному на всі можливі кути в цій системі координат і розмістивши їх на координатах. Якби ви намалювали лінію навколо, що з'єднує всі головки всіх векторів разом, ви отримаєте коло радіуса один.

    Положення, переміщення, швидкість та прискорення як вектори

    Положення, переміщення, швидкість та прискорення можуть бути показані векторами, оскільки вони визначені за величиною та напрямком.

    цілі навчання

    • Вивчіть застосування векторів при аналізі фізичних величин

    Використання векторів

    Вектори можуть бути використані для представлення фізичних величин. Найчастіше у фізиці вектори використовуються для представлення зміщення, швидкості та прискорення. Вектори являють собою комбінацію величини і напрямку, і малюються у вигляді стрілок. Довжина представляє величину, а напрямок цієї величини - напрямок, в якому вектор спрямований. Оскільки вектори будуються таким чином, корисно аналізувати фізичні величини (з розміром і напрямком) як вектори.

    Додатки

    У фізиці вектори корисні, оскільки вони можуть візуально представляти положення, переміщення, швидкість і прискорення. При малюванні векторів часто не вистачає місця, щоб намалювати їх до масштабу, який вони представляють, тому важливо десь позначити, в якому масштабі вони малюються. Наприклад, при малюванні вектора, який представляє величину 100, можна провести лінію довжиною 5 одиниць в масштабі\(\frac{1}{20}\). Коли зворотна шкала множиться на намальовану величину, вона повинна дорівнювати фактичній величині.

    Положення і переміщення

    Зсув визначається як відстань, в будь-якому напрямку, об'єкта щодо положення іншого об'єкта. Фізики використовують поняття вектора положення як графічний інструмент для візуалізації переміщень. Вектор позиції виражає позицію об'єкта від початку системи координат. Вектор положення також може бути використаний для відображення положення об'єкта по відношенню до контрольної точки, вторинного об'єкта або початкового положення (якщо аналізувати, наскільки об'єкт перемістився від початкового місця розташування). Вектор положення - це пряма лінія, проведена від довільного початку до об'єкта. Після малювання вектор має довжину і напрямок відносно використовуваної системи координат.

    Швидкість

    Швидкість також визначається через величину і напрямок. Щоб сказати, що щось набирає або втрачає швидкість, потрібно також сказати, скільки і в якому напрямку. Наприклад, літак, що летить на 200\(\mathrm{\frac{km}{h}}\) на північний схід, може бути представлений вектором, що вказує в північно-східному напрямку з величиною 200\(\mathrm{\frac{km}{h}}\). При малюванні вектора величина важлива лише як спосіб порівняння двох векторів однакових одиниць. Так, якщо на південному заході пролетів ще один літак 100\(\mathrm{\frac{km}{h}}\), векторна стрілка повинна бути вдвічі менше і спрямована в напрямку південно-західного заходу.

    Прискорення

    Прискорення, будучи тимчасовою швидкістю зміни швидкості, складається з величини і напрямку, і малюється з тією ж концепцією, що і вектор швидкості. Значення для прискорення не було б корисним у фізиці, якби величина і напрямок цього прискорення були невідомими, тому ці вектори важливі. На діаграмі вільного тіла, наприклад, падіння об'єкта, було б корисно використовувати вектор прискорення поблизу об'єкта, щоб позначити його прискорення до землі. Якщо гравітація є єдиною силою, що діє на об'єкт, цей вектор буде спрямований вниз з величиною 9,81\(\mathrm{\frac{m}{s^2}}\) або 32,2\(\mathrm{\frac{ft}{s^2}}\).

    зображення

    Векторна діаграма: Ось людина, що йде на пагорб. Його напрямок руху визначається кутом тета щодо вертикальної осі і довжиною стрілки, що йде вгору по височині. Він також прискорюється вниз під дією сили тяжіння.

    Ключові моменти

    • Вектори можна розбити на дві складові: величину і напрямок.
    • Беручи вектор, який потрібно аналізувати як гіпотенузу, горизонтальну та вертикальну складові можна знайти, заповнивши прямокутний трикутник. Нижній край трикутника - горизонтальна складова, а сторона, протилежна куту, - вертикальна складова.
    • Кут, який вектор робить з горизонталлю, може бути використаний для обчислення довжини двох компонентів.
    • Скаляри - це фізичні величини, представлені одним числом і без напрямку.
    • Вектори - це фізичні величини, які вимагають як величини, так і напрямки.
    • Приклади скалярів включають висоту, масу, площу та об'єм. Приклади векторів включають зміщення, швидкість і прискорення.
    • Щоб додати вектори, покладіть перший на набір осей з хвостом біля початку. Помістіть наступний вектор хвостом на голову попереднього вектора. Коли векторів більше немає, проведіть пряму лінію від початку до голови останнього вектора. Цей рядок є сумою векторів.
    • Щоб відняти вектори, продовжуйте так, ніби додаючи два вектори, але переверніть вектор, який потрібно віднімати по осях, а потім з'єднайте його хвіст до голови, ніби додаючи.
    • Додавання або віднімання будь-якої кількості векторів дає результуючий вектор.
    • Вектори можуть бути розкладені на горизонтальні і вертикальні складові.
    • Після того, як вектори розкладаються на компоненти, компоненти можуть бути додані.
    • Додавання відповідних компонентів двох векторів дає вектор, який є сумою двох векторів.
    • Вектор - це величина як з величиною, так і з напрямком.
    • Скаляр - це величина, яка має тільки величину.
    • Множення вектора на скаляр еквівалентно множенню величини вектора на скаляр. Вектор подовжується або зменшується, але не змінює напрямок.
    • Одиничний вектор - це вектор величини (довжини) 1.
    • Скаляр - це фізична величина, яка може бути представлена одним числом. На відміну від векторів, скаляри не мають напрямку.
    • Множення вектора на скаляр - це те саме, що і множення величини вектора на число, представлене скаляром.
    • Вектори - це стрілки, що складаються з величини і напрямку. Вони використовуються у фізиці для представлення фізичних величин, які також мають як величину, так і напрямок.
    • Зсув - це фізичний термін, що означає відстань об'єкта від контрольної точки. Оскільки зміщення містить дві частини інформації: відстань від контрольної точки і напрямок в сторону від точки, воно добре представлено вектором.
    • Швидкість визначається як швидкість зміни часу переміщення. Щоб знати швидкість об'єкта, потрібно знати, як швидко змінюється зміщення, так і в якому напрямку. Тому він також добре представлений вектором.
    • Прискорення, будучи швидкістю зміни швидкості, також вимагає як величини, так і напрямку щодо деяких координат.
    • При малюванні векторів часто не вистачає місця, щоб намалювати їх до масштабу, який вони представляють, тому важливо десь позначити, в якому масштабі вони малюються.

    Ключові умови

    • координати: Числа, що вказують на позицію відносно якоїсь осі. Наприклад:\(\mathrm{x}\) і\(\mathrm{y}\) координати вказують положення щодо осей xx та yy.
    • вісь: уявна лінія, навколо якої об'єкт обертається або симетрично розташований.
    • величина: число, присвоєне вектору, що вказує його довжину.
    • Осі координат: набір перпендикулярних ліній, які визначають координати відносно початку. Приклад: осі координат x і y визначають горизонтальне і вертикальне положення.
    • origin: Центр координатної осі, визначеної як координата 0 у всіх осях.
    • Компонент: частина вектора. Наприклад, горизонтальні і вертикальні складові.
    • вектор: Спрямована величина, одна з величиною і напрямком; між двома точками.
    • величина: число, присвоєне вектору, що вказує його довжину.
    • скалярна: величина, яка має величину, але не напрямок; порівняйте вектор.
    • одиничний вектор: вектор величини 1.
    • швидкість: Швидкість зміни зміщення по відношенню до зміни в часі.
    • Зсув: Довжина і напрямок прямої лінії між двома об'єктами.
    • прискорення: швидкість, з якою швидкість тіла змінюється з часом

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ