8.7: Поліноми Тейлора
- Page ID
- 60727
Розглянемо функцію\(y=f(x)\) і точку\(\left(c,f(c)\right)\). Похідна\(f^\prime(c)\), дає миттєву швидкість зміни\(f\) at\(x=c\). З усіх ліній, що проходять через точку\(\left(c,f(c)\right)\), лінія, яка найкраще наближається\(f\) в цій точці, є дотичною лінією; тобто лінією, нахил якої (швидкість зміни) дорівнює\(f^\prime(c)\).
На\(\PageIndex{1}\) малюнку ми бачимо функцію з\(y=f(x)\) графіком. Таблиця під графіком показує, що\(f(0)=2\) і\(f^\prime(0) = 1\); отже, дотична лінія до\(f\) at\(x=0\) є\(p_1(x) = 1(x-0)+2 = x+2\). Дотична лінія також наведена на малюнку. Зверніть увагу, що «поруч»\(x=0\),\(p_1(x) \approx f(x)\); тобто дотична лінія\(f\) добре наближається.
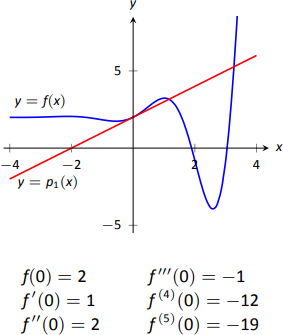
Одним з недоліків цього наближення є те, що дотична лінія відповідає лише нахилу\(f\); вона, наприклад, не відповідає увігнутості\(f\). Ми можемо знайти многочлен\(p_2(x)\), який відповідає увігнутості без особливих труднощів. Таблиця на малюнку 8.16 дає наступну інформацію:
\[f(0) = 2 \qquad f^\prime(0) = 1\qquad f^{\prime\prime}(0) = 2.\]
Тому ми хочемо,\(p_2(x)\) щоб наш многочлен мав ці самі властивості. Тобто нам потрібно
\[p_2(0) = 2 \qquad p_2'(0) = 1 \qquad p_2''(0) = 2.\]
Це просто проблема початкового значення. Ми можемо вирішити це за допомогою методів, вперше описаних у розділі 5.1. Щоб бути\(p_2(x)\) максимально простим, будемо вважати, що не тільки\(p_2''(0)=2\), але і те\(p_2''(x)=2\). Тобто друга похідна від\(p_2\) - постійна.
Якщо\(p_2''(x) = 2\), то\(p_2'(x) = 2x+C\) для якоїсь постійної\(C\). Оскільки ми це визначили\(p_2'(0) = 1\), ми знаходимо, що\(C=1\) і так\(p_2'(x) = 2x+1\). Нарешті, ми можемо обчислити\(p_2(x) = x^2+x+C\). Використовуючи наші початкові значення, ми знаємо\(p_2(0) = 2\) так\(C=2.\) Ми робимо висновок, що\(p_2(x) = x^2+x+2.\) Ця функція побудована з на\(f\) малюнку\(\PageIndex{2}\).
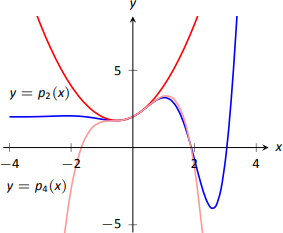
Ми можемо повторити цей процес наближення, створивши поліноми вищого ступеня, які відповідають більшій кількості похідних\(f\) at\(x=0\). Загалом, поліном ступеня\(n\) може бути створений для відповідності першим\(n\) похідним\(f\). На малюнку\(\PageIndex{2}\) також показано\(p_4(x)= -x^4/2-x^3/6+x^2+x+2\), чиї перші чотири похідні при 0 збігаються з тими\(f\). (Використовуючи таблицю на малюнку\(\PageIndex{1}\), почніть з\(p_4^{(4)}(x)=-12\) та вирішіть пов'язану проблему початкового значення.)
Оскільки ми використовуємо все більше і більше похідних, наше поліноміальне наближення\(f\) стає все краще і краще. У цьому прикладі інтервал, на якому наближення є «хорошим», стає все більшим і більшим. Малюнок\(\PageIndex{3}\) показує\(p_{13}(x)\); ми можемо візуально стверджувати, що цей многочлен\(f\) дуже добре наближається\([-2,3]\).
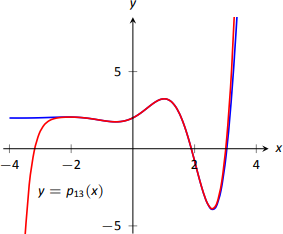
Многочлен не\(p_{13}(x)\) особливо «приємний». Це
\[ p_{13} = \dfrac{16901x^{13}}{6227020800}+\dfrac{13x^{12}}{1209600}-\dfrac{1321x^{11}}{39916800}-\dfrac{779x^{10}}{1814400}-\dfrac{359x^9}{362880}+\dfrac{x^8}{240}+\dfrac{139x^7}{5040}+\dfrac{11 x^6}{360}-\dfrac{19x^5}{120}-\dfrac{x^4}{2}-\dfrac{x^3}{6}+x^2+x+2.\]
Створені нами поліноми є прикладами поліномів Тейлора, названих на честь британського математика Брука Тейлора, який зробив важливі відкриття щодо таких функцій. Хоча ми створили вищезазначені поліноми Тейлора, вирішуючи початкові задачі, можна показати, що поліноми Тейлора слідують загальній схемі, що робить їх формування набагато більш прямим. Це описано в наступному визначенні.
Визначення 38: Поліноми Тейлора та поліноми Маклорена
\(f\)Дозволяти функція, чиї перші\(n\) похідні існують в\(x=c\).
- Поліном Тейлора\(n\) ступеня\(f\) at\(x=c\) є\[p_n(x) = f(c) + f^\prime(c)(x-c) + \dfrac{f^{\prime\prime}(c)}{2!}(x-c)^2+\dfrac{f^{\prime\prime\prime}(c)}{3!}(x-c)^3+\cdots+\dfrac{f\,^{(n)}(c)}{n!}(x-c)^n.\]
- Окремим випадком многочлена Тейлора є многочлен Маклорена, де\(c=0\). Тобто поліном Маклорена\(n\) ступеня\(f\) є\[p_n(x) = f(0) + f^\prime(0)x + \dfrac{f^{\prime\prime}(0)}{2!}x^2+\dfrac{f^{\prime\prime\prime}(0)}{3!}x^3+\cdots+\dfrac{f\,^{(n)}(0)}{n!}x^n.\]
Ми будемо практикувати створення поліномів Тейлора і Маклорена в наступних прикладах.
Приклад\(\PageIndex{1}\): Finding and using Maclaurin polynomials
- Знайдіть\(n^\text{th}\) многочлен Маклорена для\(f(x) = e^x\).
- Використовуйте\(p_5(x)\) для наближення значення\(e\).
Рішення
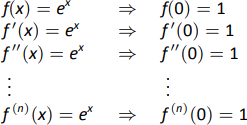
- Почнемо зі створення таблиці похідних\(e^x\) оцінюваних на\(x=0\). В даному конкретному випадку це відносно просто, як показано на малюнку 8.19.
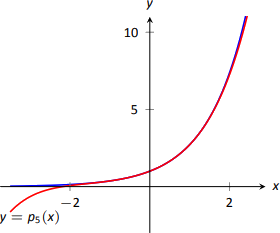
За визначенням ряду Маклорена ми маємо\[\begin{align*}p_n(x) &= f(0) + f^\prime(0)x + \dfrac{f^{\prime\prime}(0)}{2!}x^2+\dfrac{f^{\prime\prime\prime}(0)}{3!}x^3+\cdots+\dfrac{f\,^n(0)}{n!}x^n\\&= 1+x+\dfrac{1}{2}x^2+\dfrac{1}{6}x^3 + \dfrac{1}{24}x^4 + \cdots + \dfrac{1}{n!}x^n.\end{align*}\] - Використовуючи нашу відповідь з частини 1, ми повинні\[p_5 = 1+x+\dfrac{1}{2}x^2+\dfrac{1}{6}x^3 + \dfrac{1}{24}x^4 + \dfrac{1}{120}x^5.\] наблизити значення\(e\), зверніть увагу, що\(e = e^1 = f(1) \approx p_5(1).\) Це дуже просто оцінити\(p_5(1)\):\[p_5(1) = 1+1+\dfrac12+\dfrac16+\dfrac1{24}+\dfrac1{120} = \dfrac{163}{60} \approx 2.71667.\]
Ділянка\(f(x)=e^x\) і\(p_5(x)\) наведено на малюнку\(\PageIndex{5}\).
Приклад\(\PageIndex{2}\): Finding and using Taylor polynomials
- Знайдіть поліном\(n^\text{th}\) Тейлора\(y=\ln x\) at\(x=1\).
- Використовуйте\(p_6(x)\) для наближення значення\(\ln 1.5\).
- Використовуйте\(p_6(x)\) для наближення значення\(\ln 2\).
Рішення
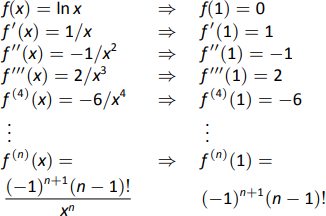
- Почнемо зі створення таблиці похідних\(\ln x\) оцінюваних в\(x=1\). Хоча це не так просто, як це було в попередньому прикладі, візерунок з'являється, як показано на малюнку\(\PageIndex{6}\).
Використовуючи Definition 38, ми маємо\[\begin{align*}p_n(x) &= f(c) + f^\prime(c)(x-c) + \dfrac{f^{\prime\prime}(c)}{2!}(x-c)^2+\dfrac{f^{\prime\prime\prime}(c)}{3!}(x-c)^3+\cdots+\dfrac{f\,^n(c)}{n!}(x-c)^n\\&= 0+(x-1)-\dfrac12(x-1)^2+\dfrac13(x-1)^3-\dfrac14(x-1)^4+\cdots+\dfrac{(-1)^{n+1}}{n}(x-1)^n.\end{align*}\] Примітка, як коефіцієнти\((x-1)\) термінів виявляються «приємними». - Ми можемо обчислити,\(p_6(x)\) використовуючи нашу роботу вище:\[p_6(x) = (x-1)-\dfrac12(x-1)^2+\dfrac13(x-1)^3-\dfrac14(x-1)^4+\dfrac15(x-1)^5-\dfrac16(x-1)^6.\] Оскільки\(p_6(x)\) наближається\(\ln x\) добре близько\(x=1\), ми наближаємось\(\ln 1.5 \approx p_6(1.5)\):\[\begin{align*}p_6(1.5) &= (1.5-1)-\dfrac12(1.5-1)^2+\dfrac13(1.5-1)^3-\dfrac14(1.5-1)^4+\cdots \\&\cdots +\dfrac15(1.5-1)^5-\dfrac16(1.5-1)^6\\&=\dfrac{259}{640}\\&\approx 0.404688.\end{align*}\] Це гарне наближення, оскільки калькулятор показує, що\(\ln 1.5 \approx 0.4055.\) рисунок\(\PageIndex{7}\) малюнка\(y=\ln x\) з\(y=p_6(x)\). Ми можемо це бачити\(\ln 1.5\approx p_6(1.5)\).
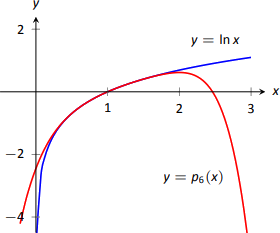
- Ми наближаємося\(\ln 2\) з\( p_6(2)\):\[\begin{align*}p_6(2) &= (2-1)-\dfrac12(2-1)^2+\dfrac13(2-1)^3-\dfrac14(2-1)^4+\cdots \\&\cdots +\dfrac15(2-1)^5-\dfrac16(2-1)^6\\&= 1-\dfrac12+\dfrac13-\dfrac14+\dfrac15-\dfrac16 \\&= \dfrac{37}{60}\\ &\approx 0.616667.\end{align*}\] Це наближення не дуже вражає: ручний калькулятор показує, що\(\ln 2 \approx 0.693147.\) Графік на малюнку 8.22 показує, що\(p_6(x)\) забезпечує менш точні наближення\(\ln x\) як\(x\) наближається до 0 або 2.
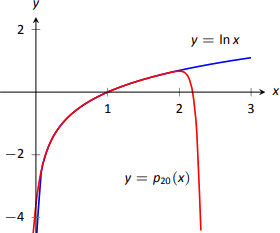
Як не дивно, навіть поліном Тейлора 20\(^\text{th}\) градусів не може наблизитися до\(x>2\), як показано\(\ln x\) на малюнку\(\PageIndex{8}\). Ми скоро обговоримо, чому це так.
Поліноми Тейлора використовуються для наближення функцій\(f(x)\) в основному в двох ситуаціях:
- Коли\(f(x)\) відомо, але, можливо, «важко» обчислити безпосередньо. Наприклад, ми можемо визначити\(y=\cos x\) як співвідношення сторін прямокутного трикутника («суміжних над гіпотенузою») або з одиничним колом. Однак жодне з них не забезпечує зручного способу обчислень\(\cos 2\). Поліном Тейлора досить високого ступеня може забезпечити розумний метод обчислення таких значень, використовуючи тільки операції, які зазвичай жорстко підключені в комп'ютер (\(+\),\(-\),\(\times\) і\(\div\)).
- Коли\(f(x)\) невідомо, але інформація про його похідних відома. Це відбувається частіше, ніж можна подумати, особливо при вивченні диференціальних рівнянь.
Незважаючи на те, що поліноми Тейлора можуть бути використані в калькуляторах та комп'ютерах для обчислення значень тригонометричних функцій, на практиці вони, як правило, не є. Розроблено й інші більш ефективні та точні методи, такі як алгоритм CORDIC.
В обох ситуаціях критичною інформацією є «Наскільки добре моє наближення?» Якщо ми використовуємо поліном Тейлора для обчислення\(\cos 2\), як ми знаємо, наскільки точним є наближення?
У нас була така ж проблема при вивченні числового інтегрування. Теорема 43 надала межі похибки при використанні, скажімо, Правила Сімпсона для наближення певного інтеграла. Ці межі дозволили нам визначити, що, наприклад, за допомогою\(10\) підінтервалів забезпечується\(\pm .01\) наближення в межах точного значення. Наступна теорема дає подібні межі для поліномів Тейлора (і, отже, Маклорена).
ТЕОРЕМА 76: ТЕОРЕМА ТЕЙЛОРА
- \(f\)Дозволяти функція,\(n+1^\text{th}\) похідна якої існує на інтервалі\(I\) і нехай\(c\) бути в\(I\). Тоді, для кожного\(x\) в\(I\), існує\(z_x\) між\(x\) і\(c\) такими, що
\[f(x) = f(c) + f^\prime(c)(x-c) + \dfrac{f^\prime (c)}{2!}(x-c)^2+ \cdots +\dfrac{f\,^{(n)}(c)}{n!}(x-c)^n+R_n(x),\]
де\( R_n(x) = \dfrac{f\,^{(n+1)}(z_x)}{(n+1)!}(x-c)^{(n+1)}.\) - \( \big|R_n(x)\big| \leq \dfrac{\max\left|\,f\,^{(n+1)}(z)\right|}{(n+1)!}\big|(x-c)^{(n+1)}\big|\)
Перша частина теореми Тейлора стверджує\(f(x) = p_n(x) + R_n(x)\),\(p_n(x)\) що де\(n^\text{th}\) порядок поліном Тейлора і\(R_n(x)\) залишок, або помилка, в наближенні Тейлора. Друга частина дає межі того, наскільки великою може бути ця помилка. Якщо\((n+1)^\text{th}\) похідна велика, помилка може бути великою; якщо\(x\) далеко не\(c\), помилка також може бути великою. Однак\((n+1)!\) термін у знаменнику, як правило, гарантує, що помилка стає меншою зі\(n\) збільшенням.
Наступний приклад обчислює оцінки помилок для наближень\(\ln 1.5\) і\(\ln 2\) зроблених у прикладі 8.7.2.
Приклад\(\PageIndex{3}\): Finding error bounds of a Taylor polynomial
Використовуйте теорему 76, щоб знайти межі помилок при наближенні\(\ln 1.5\) та\(\ln 2\) з\(p_6(x)\), поліном Тейлора ступеня 6\(f(x)=\ln x\) at\(x=1\), як обчислено в прикладі 8.7.2.
Рішення
- Починаємо з наближення\(\ln 1.5\) с\(p_6(1.5)\). Теорема посилається на відкритий інтервал\(I\), який містить обидва\(x\) і\(c\). Чим менший інтервал ми використовуємо, тим краще; це дасть нам більш точний (і менший!) наближення помилки. Дозволимо\(I = (0.9,1.6)\), так як цей інтервал містить обидва\(c=1\) і\(x=1.5\).
Теорема посилання\(\max\big|f\,^{(n+1)}(z)\big|\). У нашій ситуації це питання: «Наскільки великою може\(y=\ln x\) бути\(7^\text{th}\) похідна від проміжку\((0.9,1.6)\)?» Сьома похідна -\(y = -6!/x^7\). Найбільша величина, яку вона досягає\(I\), становить близько 1506. Таким чином, ми можемо пов'язати помилку як:\[\begin{align*}\big|R_6(1.5)\big| &\leq \dfrac{\max\big|f\,^{(7)}(z)\big|}{7!}\big|(1.5-1)^7\big|\\&\leq \dfrac{1506}{5040}\cdot\dfrac1{2^7}\\&\approx 0.0023.\end{align*}\]
Ми обчислювали\(p_6(1.5) = 0.404688\); використовуючи калькулятор, ми знаходимо\(\ln 1.5 \approx 0.405465\), так що фактична помилка приблизно\(0.000778\), яка менше, ніж наша межа\(0.0023\). Це підтверджує теорему Тейлора; теорема стверджує, що наше наближення буде в межах приблизно 2 тисячних частин від фактичного значення, тоді як наближення було насправді ближче.
- Знову знаходимо інтервал\(I\), який містить обидва\(c=1\) і\(x=2\); вибираємо\(I = (0.9,2.1)\). Максимальне значення сьомої похідної\(f\) на цьому інтервалі знову близько 1506 (так як наближаються найбільші значення\(x=0.9\)). Таким\[\begin{align*}\big| R_6(2)\big| &\leq \dfrac{\max\big|f\,^{(7)}(z)\big|}{7!}\big|(2-1)^7\big|\\&\leq \dfrac{1506}{5040}\cdot1^7\\&\approx 0.30.\end{align*}\]
чином, це пов'язано не так добре, як раніше. Використання полінома Тейлора 6 ступеня при\(x =1\) приведе нас до 0,3 правильної відповіді. Як\(p_6(2)\approx 0.61667\), наша оцінка помилок гарантує, що фактичне значення\(\ln 2\) знаходиться десь між\(0.31667\) і\(0.91667\). Ці межі не особливо корисні.
Насправді наше наближення було вимкнено лише приблизно на 0,07. Однак ми наближаємося нібито тому, що не знаємо реальної відповіді. Для того, щоб бути впевненим, що у нас є гарне наближення, нам доведеться вдатися до використання полінома вищого ступеня.
Знову практикуємося. Цього разу ми використовуємо теорему Тейлора, щоб знайти\(n\), що гарантує, що наше наближення знаходиться в межах певної суми.
Приклад\(\PageIndex{4}\): Finding sufficiently accurate Taylor polynomials
Знайдіть\(n\) таке, що поліном\(n^\text{th}\) Тейлора\(f(x)=\cos x\) at\(x=0\)\(\cos 2\) наближається до межах\(0.001\) фактичної відповіді. Що таке\(p_n(2)\)?
Рішення
Слідуючи теоремі Тейлора, нам потрібні межі на розмір похідних\(f(x)=\cos x\). У випадку з цією тригонометричною функцією це зробити нескладно. Всі похідні косинуса є\(\pm \sin x\) або\(\pm \cos x\). У всіх випадках ці функції ніколи не перевищують 1 в абсолютному значенні. Ми хочемо, щоб помилка була менше, ніж\(0.001\). Щоб знайти відповідне\(n\), розглянемо наступні нерівності:
\ [\ почати {вирівнювати*}
\ dfrac {\ max\ big|f\, ^ {(n+1)} (z)\ big|} {(n+1)!} \ big| (2-0) ^ {(n+1)}\ big| &\ leq 0,001\
\ dfrac1 {(n+1)!} \ cdot2^ {(n+1)} &\ leq 0.001
\ кінець {вирівнювати*}\]
Ми знаходимо\(n\), що задовольняє цю останню нерівність методом проб і помилок. Коли\(n=8\), ми маємо\( \dfrac{2^{8+1}}{(8+1)!} \approx 0.0014\); коли\(n=9\), ми маємо\( \dfrac{2^{9+1}}{(9+1)!} \approx 0.000282 <0.001\). Таким чином, ми хочемо наблизити\(\cos 2\) с\(p_9(2)\). \\
Тепер ми поставили собі за мету обчислити\(p_9(x)\). Нам знову потрібна таблиця похідних\(f(x)=\cos x\) оцінюваних в\(x=0\). Таблиця цих значень приведена на рис\(\PageIndex{8}\).
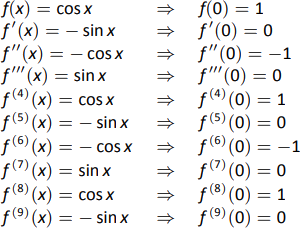
Зверніть увагу, як похідні, оцінені на\(x=0\), слідують певній схемі. Всі непарні сили\(x\) в поліномі Тейлора зникнуть, оскільки їх коефіцієнт дорівнює 0. Поки наші межі помилок стверджують, що нам потрібно\(p_9(x)\), наша робота показує, що це буде так само, як\(p_8(x)\).
Оскільки ми формуємо наш многочлен в\(x=0\), ми створюємо многочлен Маклорена, і:
\ [\ почати {вирівнювати*}
p_8 (x) &= f (0) + f^\ прайм (0) х +\ dfrac {f^ {\ прайм\ прайм} (0)} {2!} x^2 +\ dfrac {f^ {\ прайм\ прайм\ прайм} (0)} {3!} x^3 +\ cdots +\ dfrac {f\, ^ {(8)}} {8!} x^8\\
&= 1-\ dfrac {1} {2!} x^2+\ dfrac {1} {4!} x^4-\ dfrac {1} {6!} x^6+\ dfrac {1} {8!} x^8
\ end {вирівнювати*}\]
Нарешті ми наближаємо\(\cos 2\):
\[\cos 2 \approx p_8(2) = -\dfrac{131}{315} \approx -0.41587. \nonumber\]
Наша помилка пов'язана гарантує, що це наближення знаходиться в межах\(0.001\) правильної відповіді. Технологія показує нам, що наше наближення насправді знаходиться в межах\(0.0003\) правильної відповіді.
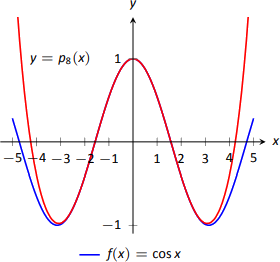
\(\PageIndex{10}\)На малюнку зображений графік\(y=p_8(x)\) і\(y=\cos x\). Зверніть увагу, наскільки добре дві функції згодні про\((-\pi,\pi)\).
Приклад\(\PageIndex{5}\): Finding and using Taylor polynomials
- Знайти поліном Тейлора 4 ступеня,\(p_4(x)\), для\(f(x)=\sqrt{x}\) at\(x=4.\)
- Використовуйте\(p_4(x)\) для наближення\(\sqrt{3}\).
- Знайти межі помилки при наближенні\(\sqrt{3}\) с\(p_4(3)\).
Рішення
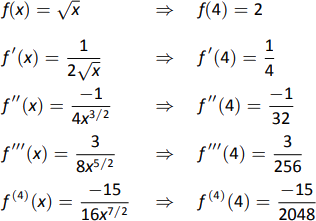
- Почнемо з оцінки похідних\(f\) at\(x=4\). Це робиться на рис\(\PageIndex{11}\). Ці значення дозволяють сформувати поліном Тейлора\(p_4(x)\):\[p_4(x) = 2 + \dfrac14(x-4) +\dfrac{-1/32}{2!}(x-4)^2+\dfrac{3/256}{3!}(x-4)^3+\dfrac{-15/2048}{4!}(x-4)^4.\]
- Як\(p_4(x) \approx \sqrt{x}\) поруч\(x=4\), ми наближаємо\(\sqrt{3}\) с\(p_4(3) = 1.73212\).
- Щоб знайти прив'язку на помилку, нам потрібен відкритий інтервал, який містить\(x=3\) і\(x=4\). Ставимо\(I = (2.9,4.1)\). Найбільше значення п'ята похідна\(f(x)=\sqrt{x}\) приймає на цьому інтервалі близько\(x=2.9\), приблизно\(0.0273\). Таким чином,\[\big|R_4(3)\big| \leq \dfrac{0.0273}{5!}\big|(3-4)^5\big| \approx 0.00023.\]
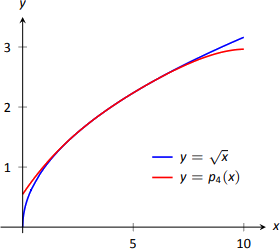
Це показує, що наше наближення є точним принаймні до перших 2 знаків після десяткової. (Виявляється, наше наближення насправді точне до 4 знаків після десяткової.) Графік\(f(x)=\sqrt x\) і\(p_4(x)\) наведено на рис\(\PageIndex{12}\). Зверніть увагу на те, як дві функції майже не відрізняються\((2,7)\).
Наш останній приклад дає короткий вступ до використання поліномів Тейлора для розв'язання диференціальних рівнянь.
Приклад\(\PageIndex{6}\): Approximating an unknown function
Функція\(y=f(x)\) невідома за винятком наступних двох фактів.
- \(y(0) = f(0) = 1\), і
- \(y^\prime= y^2\)
(Цей другий факт говорить, що дивно, похідна функції насправді функція в квадраті!)
Знайдіть поліном Маклорена 3\(p_3(x)\) ступеня\(y=f(x)\).
Рішення
Спочатку можна подумати, що недостатньо інформації дається для пошуку\(p_3(x)\). Однак зауважте, як другий факт вище насправді дозволяє нам знати, що\(y^\prime(0)\) таке:
\[y^\prime = y^2 \Rightarrow y^\prime(0) = y^2(0). \nonumber\]
З тих пір\(y(0) = 1\), ми робимо висновок, що\(y^\prime(0) = 1\).
Тепер знаходимо інформацію про\(y^{\prime\prime}\). Починаючи з\(y^\prime=y^2\), візьміть похідні обох сторін, щодо\(x\). Це означає, що ми повинні використовувати неявну диференціацію.
\ [\ почати {вирівнювати*}
y^\ правий &= y^2\
\ dfrac {d} {dx}\ лівий (y^\ правий\ правий) &=\ dfrac {d} {dx}\ лівий (y^2\ праворуч)\\
y^ {\ прайм\ прайм} &= 2y\ cdot y^\ прайм. \\
\ текст {Тепер оцініть обидві сторони за адресою\(x=0\):} &\\
y^ {\ прайм\ прайм} (0) &= 2y (0)\ cdot y^\ прайм (0)\\
y^ {\ прайм\ прайм} (0) &= 2
\ end {align*}\]
Повторюємо це ще раз, щоб знайти\(y^{\prime\prime\prime}(0)\). Ми знову використовуємо неявну диференціацію; цього разу також потрібно Правило продукту.
\ [\ почати {вирівнювати*}
\ dfrac {d} {dx}\ лівий (y^ {\ прайм\ правий}\ правий}\ правий) &=\ dfrac {d} {dx}\ ліворуч (2ррй^\ прайм\ праворуч)\\
y^ {прайм\ прайм\ прайм} &= 2y^\ cdot y^ {прайм\ прайм} &= 2y^\ cdot y^ прайм}. \\
\ текст {Тепер оцініть обидві сторони за адресою\(x=0\):} &\\
y^ {\ прайм\ прайм\ прайм} (0) &= 2y^\ прайм (0) ^2 + 2y (0) y^ {\ прайм\ прайм} (0)\\
y^ {\ прайм\ прайм\ прайм} (0) &= 2+4=6
\ кінець {align*}\]
Підсумовуючи, ми маємо:
\[y(0) = 1 \qquad y^\prime(0) = 1 \qquad y^{\prime\prime}(0) = 2 \qquad y^{\prime\prime\prime}(0) = 6. \nonumber\]
Тепер ми можемо сформувати\(p_3(x)\):
\ [\ почати {вирівнювати*}
p_3 (x) &= 1 + х +\ dfrac {2} {2!} x^2 +\ dfrac {6} {3!} х ^ 3\\
&= 1+х+х ^ 2+х ^ 3.
\ end {вирівнювати*}\]
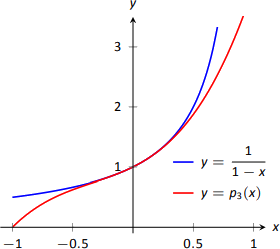
Виходить, що диференціальне рівняння\(y^\prime=y^2\), з якого ми почали\(y(0)=1\), де, можна вирішити без особливих труднощів:\( y = \dfrac{1}{1-x}\). На малюнку 8.28 показана ця функція, побудована за допомогою\(p_3(x)\). Зверніть увагу на те, наскільки вони схожі поруч\(x=0\).
Виходить за рамки цього тексту проводити аналіз помилок при використанні поліномів Тейлора для наближення розв'язків диференціальних рівнянь. Ця тема часто піднімається у вступних курсах диференціальних рівнянь і зазвичай глибоко висвітлюється в курсах чисельного аналізу. Такий аналіз дуже важливий, потрібно знати, наскільки хороша їх наближення. Ми досліджували цей приклад просто, щоб продемонструвати корисність поліномів Тейлора.
Велика частина цієї глави була присвячена вивченню нескінченних рядів. Цей розділ зробив крок назад від цього дослідження, зосередившись замість цього на кінцевому підсумовуванні термінів. У наступному розділі ми досліджуємо Серію Тейлора, де ми представляємо функцію з нескінченним рядом.
