8.8: Серія Тейлора
- Page ID
- 60728
У розділі 8.6 ми показали, як певні функції можуть бути представлені функцією рядів потужності. У 8.7 ми показали, як ми можемо наближати функції з поліномами, враховуючи, що є достатньо похідної інформації. У цьому розділі ми поєднуємо ці поняття: якщо функція\(f(x)\) нескінченно диференційовна, ми покажемо, як представляти її за допомогою функції степеневого ряду.
Визначення 39 серій Тейлора та Маклорина
Нехай\(f(x)\) є похідні від усіх замовлень на\(x=c\).
- Серія Тейлора\(f(x)\), \(c\)зосереджена на\[\sum_{n=0}^\infty \frac{f\,^{(n)}(c)}{n!}(x-c)^n.\]
- Налаштування\(c=0\) дає серії Maclaurin\(f(x)\):\[\sum_{n=0}^\infty \frac{f\,^{(n)}(0)}{n!}x^n.\]
Різниця між поліномом Тейлора та рядом Тейлора полягає в тому, що перший є поліномом, що містить лише скінченну кількість членів, тоді як останній - це ряд, підсумовування нескінченної множини термінів. При створенні полінома Тейлора ступеня\(n\) для функції\(f(x)\) в\(x=c\), нам потрібно було оцінити\(f\), і перші\(n\) похідні\(f\), в\(x=c\) .При створенні ряду Тейлора\(f\), це допомагає знайти закономірність, яка описує\(n^\text{th}\) похідне від\(f\) at\(x=c\) .Ми демонструємо це в наступних двох прикладах.
Приклад\(\PageIndex{1}\): The Maclaurin series of \(f(x) = \cos x\)
Знайдіть серію Маклорен\(f(x)=\cos x\).
Розв'язок У прикладі 8.7.4 ми знайшли\(8^\text{th}\) ступінь полінома Маклорена від\(\cos x\) .При цьому ми створили таблицю, наведену на малюнку 8.29.
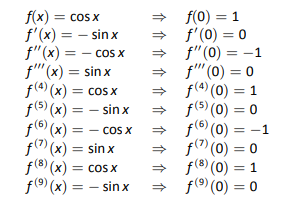
Зверніть увагу, як\(f\,^{(n)}(0)=0\) коли\(n\) непарний,\(f\,^{(n)}(0)=1\) коли\(n\) ділиться на\(4\), а\(f\,^{(n)}(0)=-1\) коли\(n\) парний, але не ділиться на 4. Таким чином, серія\(\cos x\) Маклорен
\[1-\frac{x^2}2+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!} - \cdots\]
Ми можемо піти далі і написати це як підсумок. Оскільки нам потрібні лише терміни, де потужність парна, ми пишемо ряд потужності з точки зору\(x^{2n}\):\(x\)
\[\sum_{n=0}^\infty (-1)^{n}\frac{x^{2n}}{(2n)!}.\]
Приклад\(\PageIndex{2}\): The Taylor series of \(f(x)=\ln x\) at \(x=1\)
Знайдіть серію Тейлора з\(f(x) = \ln x\) центром на\(x=1\).
Рішення
Рисунок 8.30 показує\(n^\text{th}\) похідну\(\ln x\) оціненої при\(x=1\) for\(n=0,\ldots,5\) разом з виразом для\(n^\text{th}\) терміна:\[f\,^{(n)}(1) = (-1)^{n+1}(n-1)!\quad \text{for \(n\geq 1\).}\] Пам'ятайте, що саме це відрізняє ряд Тейлора від поліномів Тейлора; нас дуже цікавить знаходження закономірності для\(n^\text{th}\) терміна, а не просто знаходження скінченної множини коефіцієнтів для полінома.
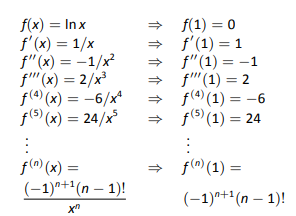
Оскільки\(f(1) = \ln 1 = 0\) ми пропускаємо перший термін і починаємо підсумовування з\(n=1\), даючи серії Тейлора для\(\ln x\), зосереджені на\(x=1\), як
\[\sum_{n=1}^\infty (-1)^{n+1}(n-1)!\frac{1}{n!}(x-1)^n = \sum_{n=1}^\infty (-1)^{n+1}\frac{(x-1)^n}{n}. \]
Важливо зазначити, що визначення 39 визначає ряд Тейлора, заданий функцією\(f(x)\); однак ми ще не можемо констатувати, що\(f(x)\) дорівнює його ряду Тейлора. Ми виявимо, що «більшу частину часу» вони рівні, але потрібно враховувати умови, які дозволяють зробити висновок про це.
Теорема 76 стверджує, що похибка між функцією\(f(x)\) та її поліномом Тейлора\(n^\text{th}\) —ступеня\(p_n(x)\) є\(R_n(x)\), де
\[ \big|R_n(x)\big| \leq \frac{\max\left|\,f\,^{(n+1)}(z)\right|}{(n+1)!}\big|(x-c)^{(n+1)}\big|.\]
Якщо\(R_n(x)\) йде до 0 для кожного\(x\) в інтервалі, коли\(I\)\(n\) наближається до нескінченності, ми робимо висновок, що функція дорівнює її розширенню рядів Тейлора.
теорема 77 функція і рівність рядів Тейлора
Дозволяти\(f(x)\) мати похідні всіх порядків в\(x=c\), нехай\(R_n(x)\) буде, як зазначено в теоремі 76, і нехай\(I\) буде інтервал, на якому серія Тейлора\(f(x)\) сходиться.
Якщо\(\lim\limits_{n\to\infty} R_n(x) = 0\) для всіх\(x\) в\(I\), то\[f(x) = \sum_{n=0}^\infty \frac{f\,^{(n)}(c)}{n!}(x-c)^n\ \text{ on \(I\).}\]
Продемонстровано використання цієї теореми на прикладі.
Приклад\(\PageIndex{3}\): Establishing equality of a function and its Taylor series
Покажіть, що\(f(x) = \cos x\) дорівнює його серії Маклорена, як показано в прикладі 8.8.1, для всіх\(x\).
Рішення
За заданим значенням\(x\) величина терміна похибки\(R_n(x)\) обмежена
\[ \big|R_n(x)\big| \leq \frac{\max\left|\,f\,^{(n+1)}(z)\right|}{(n+1)!}\big|x^{n+1}\big|.\]
Оскільки всі\(\cos x\) похідні від є\(\pm \sin x\) або\(\pm\cos x\), чиї величини обмежені\(1\), ми можемо констатувати
\[ \big|R_n(x)\big| \leq \frac{1}{(n+1)!}\big|x^{n+1}\big|\]
що має на увазі
\[ -\frac{|x^{n+1}|}{(n+1)!} \leq R_n(x) \leq\frac{|x^{n+1}|}{(n+1)!}.\label{eq:coseqtaylor}\]
Для будь-якого\(x\),\(\lim\limits_{n\to\infty} \frac{x^{n+1}}{(n+1)!} = 0\). Застосовуючи теорему стискання до рівняння\ ref {eq:coseqtaylor}, ми робимо висновок, що\( \lim\limits_{n\to\infty} R_n(x) = 0\) для всіх\(x\), а значить
\[\cos x = \sum_{n=0}^\infty (-1)^{n}\frac{x^{2n}}{(2n)!}\quad \text{for all \(x\)}.\]
Природно припустити, що функція дорівнює її ряду Тейлора на інтервалі збіжності ряду, але це не так. Для того щоб правильно встановити рівність, потрібно використовувати теорему 77. Це трохи розчаровує, оскільки ми розробили прекрасні методи визначення інтервалу збіжності степеневого ряду, і доведення того, що\(R_n(x)\to 0\) може бути громіздким, оскільки він має справу з похідними функції високого порядку.
Є хороші новини. Функція,\(f(x)\) яка дорівнює її серії Тейлора, зосереджена в будь-якій точці області, як кажуть\(f(x)\), є аналітичною функцією, і більшість, якщо не всі, функції, які ми стикаємося в цьому курсі, є аналітичними функціями. Взагалі кажучи, будь-яка функція, яку створюється з елементарними функціями (поліномами, експоненціальними, тригонометричними функціями тощо), яка не є кусково визначеною, є, ймовірно, аналітичною. Для більшості функцій ми припускаємо, що функція дорівнює її ряду Тейлора на інтервалі збіжності ряду і використовуємо теорему 77 лише тоді, коли ми підозрюємо, що щось може працювати не так, як очікувалося.
Розробляємо ряд Тейлора для ще однієї важливої функції, потім наведемо таблицю ряду Тейлора для ряду загальних функцій.
Приклад\(\PageIndex{4}\): The Binomial Series
Знайдіть серію Маклорен\(f(x) = (1+x)^k\),\(k\neq 0\).
Рішення
Коли\(k\) є натуральним числом, ряд Маклорен є кінцевим. Наприклад, коли\(k=4\), у нас є
\[f(x) = (1+x)^4 = 1+4x+6x^2+4x^3+x^4.\]
Коефіцієнти\(x\) коли\(k\) є додатним цілим числом відомі як біноміальні коефіцієнти, даючи ряд, який ми розробляємо його назву.
Коли\(k=1/2\), ми\(f(x) = \sqrt{1+x}\) має.Знаючи серійне подання цієї функції дасть корисний спосіб наближення\(\sqrt{1.3}\), наприклад.
Щоб розробити ряд Маклорена\(f(x) = (1+x)^k\) для будь-якого значення\(k\neq0\), ми розглядаємо похідні\(f\) оцінюваних при\(x=0\):
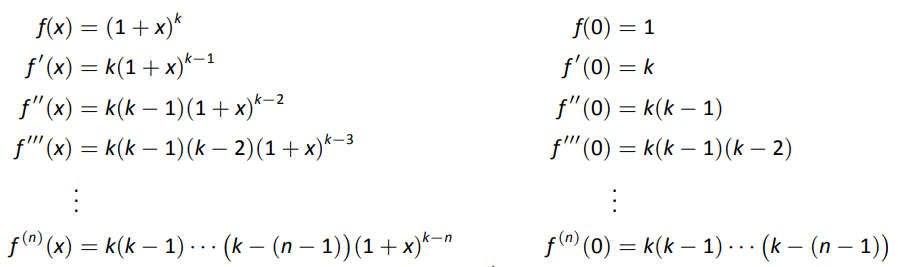
Таким чином, серія Maclaurin\(f(x) = (1+x)^k\) для
\[1+ k + \frac{k(k-1)}{2!} + \frac{k(k-1)(k-2)}{3!} + \ldots + \frac{k(k-1)\cdots\big(k-(n-1)\big)}{n!}+\ldots\]
Важливо визначити інтервал сходження цього ряду. З
\[a_n = \frac{k(k-1)\cdots\big(k-(n-1)\big)}{n!}x^n,\]
застосовуємо тест співвідношення:
\ [\ почати {вирівнювати*}
\ lim\ limits_ {n\ to\ infty}\ розрив {|a_ {n+1} |} {|a_n|} &=\ lim\ limits_ {n\ to\ infty}\ вліво |\ frac {k (k-1)\ cdots (k-n)} {(n+1)!} x^ {n+1}\ праворуч |\ Великий/\ ліво|\ frac {k (k-1)\ cdots\ великий (k- (n-1)\ великий)} {n!} x^n\ праворуч |\\
&=\ lim\ limits_ {n\ to\ infty}\ ліворуч |\ frac {k-n} {n} х\ праворуч |\\
&= |x|.
\ end {вирівнювати*}\]
Серія сходиться абсолютно, коли межа тесту коефіцієнта менше 1; отже, ми маємо абсолютну збіжність, коли\(|x|<1\).
Перебуваючи поза межами цього тексту, інтервал збіжності залежить від\(k\) значення.When\(k>0\), інтервал збіжності\([-1,1]\) становить.When\(-1<k<0\), інтервал збіжності\([-1,1)\) становить.If\(k\leq -1\), інтервал збіжності дорівнює\((-1,1)\).
Ми дізналися, що поліноми Тейлора пропонують спосіб наближення «важко обчислити» функції з поліномом. Серія Тейлора пропонує спосіб точного представлення функції з серією. Ймовірно, можна побачити використання хорошого наближення; чи є використання представлення функції саме як ряд?
Хоча ми не повинні випускати з уваги математичну красу серій Тейлора (що є достатньою підставою для їх вивчення), є і практичне застосування. Вони забезпечують цінний інструмент для вирішення різноманітних задач, включаючи проблеми, пов'язані з інтеграцією та диференціальними рівняннями.
У Key Idea 32 (на наступній сторінці) ми наведемо таблицю ряду Тейлора ряду загальних функцій. Потім ми наведемо теорему про «алгебру степеневих рядів», тобто про те, як ми можемо об'єднати ряди степенів для створення енергетичних рядів нових функцій. Це дозволяє нам знайти ряд функцій Тейлора, як,\(f(x) = e^x\cos x\) знаючи серію Тейлора\(e^x\) і\(\cos x\).
Перш ніж досліджувати функції об'єднання, розглянемо ряд Тейлора для функції арктангенса (див. Ключ Ідея 32). Знаючи це\(\tan^{-1}(1) = \pi/4\), ми можемо використовувати цей ряд для наближення значення\(\pi\):
\ [\ почати {вирівняти}
\ розрив {\ пі} 4 &=\ tan^ {-1} (1) = 1-\ frac13+\ frac15-\ frac17+\ frac19-\ cdots\\\ pi &= 4
\ ліворуч (1-\ frac13+\ frac15-\ frac17+\ frac19-\ cdots\ праворуч)
\ кінець {вирівнювання}\]
На жаль, саме це розширення\(\pi\) сходиться дуже повільно. Перші 100 термінів приблизні\(\pi\) як\(3.13159\), що не особливо добре.
КЛЮЧОВА ІДЕЯ 32 ВАЖЛИВІ РОЗШИРЕННЯ СЕРІЇ ТЕЙЛОРА

ТЕОРЕМА 78 АЛГЕБРА ПОТУЖНИХ РЯДІВ
Нехай\( f(x) = \sum_{n=0}^\infty a_nx^n\) і\( g(x) = \sum_{n=0}^\infty b_nx^n\) сходяться абсолютно для\(|x|<R\), і нехай\(h(x)\) будуть безперервними.
- \( f(x)\pm g(x) = \sum_{n=0}^\infty (a_n\pm b_n)x^n\)\ квадроцикл для\(|x|<R\).
- \( f(x)g(x) = \left(\sum_{n=0}^\infty a_nx^n\right)\left(\sum_{n=0}^\infty b_nx^n\right) = \sum_{n=0}^\infty\big(a_0b_n+a_1b_{n-1}+\ldots a_nb_0\big)x^n \text{ for }|x|<R\).
- \( f\big(h(x)\big) = \sum_{n=0}^\infty a_n\big(h(x)\big)^n \quad \text{ for }|h(x)|<R\).
Приклад\(\PageIndex{5}\): Combining Taylor series
Випишіть перші 3 терміни серії Тейлора для\(f(x) = e^x\cos x\) використання Key Idea 32 та теореми 78.
Рішення
Ключова ідея 32 повідомляє нам, що
\[e^x = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\quad \text{and}\quad \cos x = 1-\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots.\]
Застосовуючи теорему 78, ми знаходимо, що
\ (\ begin {вирівнювання}
e^x\ cos х &=\ лівий (1+x+\ frac {x^2} {2!} +\ гідророзриву {x^3} {3!} +\ cdots\ праворуч)\ ліворуч (1-\ frac {x^2} {2!} +\ гідророзриву {x^4} {4!} +\ cdots\ праворуч). \\
\ text {Розподілити} &\ text {вираз правої руки по лівому краю:}\\
&= 1\ left (1-\ frac {x^2} {2!} +\ гідророзриву {x^4} {4!} +\ cdots\ праворуч) +х\ ліворуч (1-\ frac {x^2} {2!} +\ гідророзриву {x^4} {4!} +\ cdots\ праворуч) +\ frac {x^2} {2!} \ ліворуч (1-\ розриву {x^2} {2!} +\ гідророзриву {x^4} {4!} +\ cdots\ праворуч)\\
&+\ frac {x^3} {3!} \ ліворуч (1-\ розриву {x^2} {2!} +\ гідророзриву {x^4} {4!} +\ cdots\ праворуч) +\ frac {x^4} {4!} \ ліворуч (1-\ розриву {x^2} {2!} +\ гідророзриву {x^4} {4!} +\ cdots\ право) +\ cdots\\
&\ text {Розподілити знову і збирати подібні терміни.} \\
&= 1 + х -\ розрив {x^3} {3} -\ розрив {x^4} {6} -\ гідророзриву {x^5} {30} +\ гідророзриву {x^7} {630} +\ cdots
\ end {вирівнювання}\)
Хоча цей процес трохи виснажливий, він набагато швидше, ніж оцінка всіх необхідних похідних\(e^x\cos x\) і обчислення серії Тейлора безпосередньо.
Оскільки серія для\(e^x\) і\(\cos x\) обидва сходяться\((-\infty,\infty)\), так само і розширення серії для\(e^x\cos x\).
Приклад\(\PageIndex{6}\): Creating new Taylor series
Використовуйте теорему 78 для створення рядів для\(y=\sin(x^2)\) і\(y=\ln (\sqrt{x})\).
Рішення
Враховуючи, що
\[\sin x = \sum_{n=0}^\infty (-1)^n\frac{x^{2n+1}}{(2n+1)!} = x-\frac{x^3}{3!}+\frac{x^5}{5!} -\frac{x^7}{7!}+\cdots,\]
ми просто\(x^2\) підставляємо\(x\) в серії, даючи
\[\sin (x^2) = \sum_{n=0}^\infty (-1)^n\frac{(x^2)^{2n+1}}{(2n+1)!} = x^2-\frac{x^6}{3!}+\frac{x^{10}}{5!} -\frac{x^{14}}{7!}\cdots.\]
Оскільки серія Тейлора для\(\sin x\) має нескінченний радіус зближення, так само і серія Тейлора для\(\sin(x^2)\).
Розширення Тейлора для\(\ln x\) наведеного в Key Idea 32 зосереджено на\(x=1\), тому ми\(x=1\) також будемо\(\ln (\sqrt{x})\) центрувати серію.
З
\[\ln x = \sum_{n=1}^\infty(-1)^{n+1}\frac{(x-1)^n}{n} = (x-1)- \frac{(x-1)^2}{2} +\frac{(x-1)^3}{3}-\cdots,\]
ми замінюємо\(\sqrt{x}\)\(x\) для отримання
\[\ln (\sqrt{x}) = \sum_{n=1}^\infty(-1)^{n+1}\frac{(\sqrt{x}-1)^n}{n} = (\sqrt{x}-1)- \frac{(\sqrt{x}-1)^2}{2} +\frac{(\sqrt{x}-1)^3}{3}-\cdots.\]
Хоча це не строго силовий ряд, це ряд, який дозволяє нам вивчити\(\ln(\sqrt{x})\) функцію.Оскільки інтервал збіжності\(\ln x\) є\((0,2]\), а діапазон\(\sqrt{x}\) включення\((0,4]\) є\((0,2]\), інтервал збіжності цього ряду розширення\(\ln(\sqrt{x})\) є\((0,4]\).
Примітка: У прикладі 8.8.6 можна створити серію, просто\(\ln(\sqrt{x})\) визнавши це\(\ln(\sqrt{x}) = \ln (x^{1/2}) = 1/2\ln x\), і, отже, помноживши серію Тейлора для\(\ln x\)\(1/2\) по.Цей приклад був обраний для демонстрації інших аспектів серії, таких як той факт, що інтервал конвергенції змінюється.
Приклад\(\PageIndex{7}\): Using Taylor series to evaluate definite integrals
Використовуйте серію Тейлора\(e^{-x^2}\) для оцінки\( \int_0^1e^{-x^2}\ dx\).
Рішення
При вивченні числового інтегрування ми дізналися, що\(e^{-x^2}\) не має антипохідної, що виражається в терміні елементарних функцій. Це означає, що будь-який певний інтеграл цієї функції повинен мати своє значення наближене, а не обчислене точно.
Ми можемо швидко виписати серію Тейлора для\(e^{-x^2}\) використання серії Тейлора\(e^x\):
\ [\ почати {вирівнювати*}
e^x &=\ sum_ {n=0} ^\ infty\ розрив {x^n} {n!} = 1+х+\ гідророзриву {x^2} {2!} +\ гідророзриву {x^3} {3!} +\ cdots
\\ текст {і так} &\\
e^ {-x^2} &=\ sum_ {n=0} ^\ infty\ FRAC {(-x^2) ^n} {n!} \\
&=\ sum_ {n=0} ^\ infty (-1) ^n\ розрив {x^ {2n}} {n!} \\
&= 1-x^2+\ гідророзриву {x^4} {2!} -\ гідророзриву {x^6} {3!} +\ точки.
\ end {вирівнювати*}\]
Ми використовуємо теорему 75 для інтеграції:
\[\int e^{-x^2}\ dx = C + x - \frac{x^3}{3}+\frac{x^5}{5\cdot2!}-\frac{x^7}{7\cdot3!}+\cdots +(-1)^n\frac{x^{2n+1}}{(2n+1)n!}+\cdots\]
Це антипохідне\(e^{-x^2}\); хоча ми можемо записати його як ряд, ми не можемо виписати його з точки зору елементарних функцій. Оцінити певний інтеграл можна\( \int_0^1e^{-x^2}\ dx\) за допомогою цього антипохідного; підставляючи 1 і 0 для,\(x\) а віднімання дає
\[\int_0^1e^{-x^2}\ dx = 1-\frac{1}{3}+\frac{1}{5\cdot 2!}-\frac{1}{7\cdot3!} + \frac{1}{9\cdot4!}\cdots.\]
Підсумовуючи 5 членів, показаних вище, дають наближення\(0.74749.\) Оскільки це змінний ряд, ми можемо використовувати теорему про наближення змінних рядів (Теорема 71), щоб визначити, наскільки точним є це наближення. Наступний член ряду -\( 1/(11\cdot5!) \approx 0.00075758\) .Таким чином, ми знаємо, що наше наближення знаходиться в межах\(0.00075758\) фактичного значення інтеграла. Це, можливо, набагато менше роботи, ніж використання Правило Сімпсона для наближення значення інтеграла.
Приклад\(\PageIndex{8}\): Using Taylor series to solve differential equations
Розв'яжіть диференціальне рівняння\(y^{\prime}=2y\) через степеневий ряд і використовуйте теорію ряду Тейлора для розпізнавання розв'язку з точки зору елементарної функції.
Рішення
Перші 5 членів степеневого ряду розв'язку цього диференціального рівняння ми знайшли у прикладі 8.6.5 розділу 8.6. Це:
\[a_0=1,\quad a_1 = 2,\quad a_2 = \frac42=2,\quad a_3=\frac{8}{2\cdot3}=\frac43,\quad a_4=\frac{16}{2\cdot3\cdot4} = \frac23.\]
Ми включаємо «неспрощені» вирази для коефіцієнтів, знайдених у прикладі 8.6.5, оскільки шукаємо закономірність. Можна показати, що\(a_n = 2^n/n!\) .Таким чином, рішення, записане як силовий ряд, є
\[y = \sum_{n=0}^\infty \frac{2^n}{n!}x^n = \sum_{n=0}^\infty \frac{(2x)^n}{n!}.\]
Використовуючи ключову ідею 32 та теорему 78, ми визнаємо\(f(x) = e^{2x}\):
\[e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \qquad \Rightarrow \qquad e^{2x} = \sum_{n=0}^\infty \frac{(2x)^n}{n!}.\]
Знайти закономірність у коефіцієнтах, які відповідають послідовному розширенню відомої функції, наприклад, показаних у Key Idea 32, може бути важко. Що робити, якщо коефіцієнти в попередньому прикладі були наведені в їх зменшеному вигляді; як ми могли б ще відновити функцію\(y=e^{2x}\)?
Припустимо, що все, що ми знаємо, це
\[a_0=1,\quad a_1=2,\quad a_2=2,\quad a_3=\frac43,\quad a_4=\frac23.\]
Визначення 39 стверджує, що кожен термін розширення функції Тейлора включає в себе\(n!\) .Це дозволяє сказати, що
\[a_2=2=\frac{b_2}{2!},\quad a_3 = \frac43=\frac{b_3}{3!},\quad \text{and}\quad a_4 = \frac23=\frac{b_4}{4!}\]
для деяких значень\(b_2\),\(b_3\) і\(b_4\).
Вирішуючи ці значення, ми бачимо\(b_2=4\),\(b_4=16\) що,\(b_3 = 8\) і.Тобто ми відновлюємо шаблон, який ми бачили раніше, дозволяючи нам писати
\ [\ почати {вирівнювати*}
f (x) =\ sum_ {n=0} ^\ infty a_nx^n &=\ sum_ {n=0} ^\ infty\ frac {b_n} {n!} x^n\\
&= 1+2x+\ гідророзриву {4} {2!} x^2 +\ гідророзриву {8} {3!} x^3+\ гідророзриву {16} {4!} x^4 +\ cdots
\ кінець {вирівнювати*}\]
Звідси легше розпізнати, що ряд описує експоненціальну функцію.
Існують простіші, більш прямі способи вирішення диференціального\(y^{\prime} = 2y\) рівняння.Ми застосували методи степеневих рядів до цього рівняння, щоб продемонструвати його корисність, і продовжили показувати, як іноді ми можемо відновити рішення з точки зору елементарних функцій, використовуючи теорію Тейлора серія. Більшість диференціальних рівнянь, з якими стикаються в реальних наукових та інженерних ситуаціях, набагато складніші, ніж цей, але енергетичні ряди можуть запропонувати цінний інструмент у пошуку або, принаймні, апроксимації рішення.
У цій главі введені послідовності, які представляють собою впорядковані списки чисел, за якими слідують ряди, в яких ми складаємо члени послідовності. Ми швидко побачили, що такі суми не завжди складаються в «нескінченність», а скоріше сходяться. Ми вивчали тести на збіжність, потім закінчили главу формальним способом визначення функцій на основі рядів. Такі «послідовно визначені функції» є цінним інструментом у вирішенні цілого ряду різних завдань у всій науці та техніці.
У наступних розділах з'являються нові способи визначення кривих на площині, окрім використання функцій форми.\(y=f(x)\) Криві, створені цими новими методами, можуть бути красивими, корисними та важливими.
