10.3: Серія Тейлора та Маклорена

Цілі навчання

• Опишіть процедуру знаходження полінома Тейлора заданого порядку для функції.
• Поясніть значення і значення теореми Тейлора залишком.
• Оцінити залишок для наближення ряду Тейлора заданої функції.

У попередніх двох розділах ми обговорювали, як знайти уявлення силових рядів для певних типів функцій, зокрема функцій, пов'язаних з геометричними рядами. Тут ми обговорюємо уявлення степеневих рядів для інших типів функцій. Зокрема, ми розглядаємо наступні питання: Які функції можуть бути представлені силовими рядами і як ми знаходимо такі уявлення? Якщо ми можемо знайти представлення степеневого ряду для певної функції$f$ і ряд сходиться на деякому інтервалі, як ми можемо довести, що ряд насправді сходиться до$f$?

Огляд серії Тейлор/Маклорін

Розглянемо функцію$f$, яка має представлення степеневого ряду на$x=a$. Тоді ряд має вигляд

$$\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+ \dots. \label{eq1}$$

Якими повинні бути коефіцієнти? Наразі ми ігноруємо проблеми конвергенції, але замість цього зосереджуємося на тому, якою має бути серія, якщо така існує. Ми повернемося до обговорення конвергенції пізніше в цьому розділі. Якщо ряд Equation\ ref {eq1} є представленням для$f$ at$x=a$, ми, звичайно, хочемо, щоб ряд дорівнював$f(a)$ at$x=a$. Оцінюючи серію на$x=a$, ми бачимо, що

$$\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(a−a)+c_2(a−a)^2+\dots=c_0.\label{eq2}$$

Таким чином, ряд дорівнює$f(a)$ якщо коефіцієнт$c_0=f(a)$. Крім того, ми хотіли б, щоб перша похідна рядів потужності дорівнювала$f′(a)$ при$x=a$. Диференціюючи рівняння\ ref {eq2} за терміном, ми бачимо, що

$$\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(x−a)+3c_3(x−a)^2+\dots.\label{eq3}$$

Тому у$x=a,$ похідної є

$$\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(a−a)+3c_3(a−a)^2+\dots=c_1.\label{eq4}$$

Тому похідна ряду дорівнює,$f′(a)$ якщо коефіцієнт$c_1=f′(a).$ Продовжуючи таким чином, шукаємо коефіцієнти$c_n$ такі, що всі похідні степеневого ряду Equation\ ref {eq4} будуть узгоджуватися з усіма відповідними похідними$f$ at$x=a$. Друга та третя похідні рівняння\ ref {eq3} задаються

$$\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n \right)=2c_2+3⋅2c_3(x−a)+4⋅3c_4(x−a)^2+\dots\label{eq5}$$

і

$$\dfrac{d^3}{dx^3} \left( \sum_{n=0}^∞c_n(x−a)^n \right)=3⋅2c_3+4⋅3⋅2c_4(x−a)+5⋅4⋅3c_5(x−a)^2+⋯.\label{eq6}$$

Тому при$x=a$, друга і третя похідні

$$\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=2c_2+3⋅2c_3(a−a)+4⋅3c_4(a−a)^2+\dots=2c_2\label{eq7}$$

і

$$\dfrac{d^3}{dx^3} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=3⋅2c_3+4⋅3⋅2c_4(a−a)+5⋅4⋅3c_5(a−a)^2+\dots =3⋅2c_3\label{eq8}$$

рівні$f''(a)$ і$f'''(a)$, відповідно, якщо$c_2=\dfrac{f''(a)}{2}$ і$c_3=\dfrac{f'''(a)}{3⋅2}$. Більш загально, ми бачимо, що якщо$f$ має представлення степеневого ряду на$x=a$, то коефіцієнти повинні бути задані$c_n=\dfrac{f^{(n)}(a)}{n!}$. Тобто серія повинна бути

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯ \nonumber$$

Ця силова серія для$f$ відома як серія Тейлора для$f$$a.$ If$x=0$, то ця серія відома як серія Маклорена для$f$.

Визначення$\PageIndex{1}$: Maclaurin and Taylor series

Якщо$f$ має похідні від усіх порядків at$x=a$, то серія Тейлора для функції$f$ at$a$

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯ \nonumber$$

Серія Тейлора для$f$ 0 відома як серія Маклорена для$f$.

Пізніше в цьому розділі ми покажемо приклади пошуку рядів Тейлора та обговоримо умови, за яких ряд Тейлора для функції сходиться з цією функцією. Тут ми констатуємо важливий результат. Нагадаємо, що уявлення силових рядів унікальні. Тому, якщо функція$f$ має силовий ряд на$a$, то вона повинна бути серією Тейлора для$f$ at$a$.

Унікальність серії Тейлор

Якщо функція$f$ має ряд потужності в a, який сходиться до$f$ на деякому відкритому інтервалі$a$, що містить, то ця потужність ряд є серією Тейлора для$f$ at$a$.

Доказ випливає безпосередньо з того, що обговорювалося раніше.

Щоб визначити, чи збігається ряд Тейлора, нам потрібно подивитися на його послідовність часткових сум. Ці часткові суми є скінченними многочленами, відомими як поліноми Тейлора.

Поліноми Тейлора

$n^{\text{th}}$Часткова сума ряду Тейлора для функції$f$ at$a$ відома як поліном Тейлора$n^{\text{th}}$ -ступеня. Наприклад, ^0-й, ^1-й, ^2-й і ^3-й часткові суми ряду Тейлора задаються по

$$\begin{align*} p_0(x) &=f(a) \\[4pt] p_1(x) &=f(a)+f′(a)(x−a) \\[4pt]p_2(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2\ \\[4pt]p_3(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3 \end{align*}$$

відповідно. Ці часткові суми відомі як поліноми Тейлора ^0-го, ^1-го, 1-го, ^2-го та ^3-го ступеня Тейлора$f$ at$a$ відповідно. Якщо$x=a$, то ці многочлени відомі як поліноми Маклорена для$f$. Тепер ми надаємо формальне визначення поліномів Тейлора та Маклорена для функції$f$.

Визначення$\PageIndex{2}$: Maclaurin polynomial

Якщо$f$ має$n$ похідні при$x=a$, то поліном Тейлора$n^{\text{th}}$ -ступеня$f$ at$a$ дорівнює

$$p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n. \nonumber$$

Поліном Тейлора$n^{\text{th}}$ -ступеня для$f$ at$0$ відомий як поліном Маклорена$n^{\text{th}}$ -ступеня для$f$.

Тепер ми покажемо, як використовувати це визначення, щоб знайти кілька поліномів Тейлора для$f(x)=\ln x$ at$x=1$.

Приклад$\PageIndex{1}$: Finding Taylor Polynomials

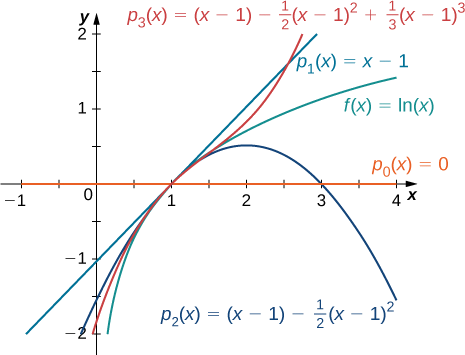
Знайдіть поліноми Тейлора$p_0,p_1,p_2$ і$p_3$ для$f(x)=\ln x$ at$x=1$. Використовуйте утиліту графіків, щоб порівняти графік$f$ з графіками$p_0,p_1,p_2$ і$p_3$.

Рішення

Щоб знайти ці поліноми Тейлора, нам потрібно оцінити$f$ і перші три його похідні в$x=1$.

\ [\ почати {вирівнювати*} f (x) &=\ ln x & f (1) &=0\\ [5pt]
f′ (x) &=\ dfrac {1} {x} & f′ (1) &= 1\\ [5pt]
f "(x) &=−\ dfrac {1} {x^2} & f" (1) &==\ −1\ [5pt]
f"' (x) &=\ dfrac {2} {x^3} & f"' (1) &=2\ кінець {вирівнювати*}\]

Тому,

$$\begin{align*} p_0(x) &= f(1)=0,\\[4pt]p_1(x) &=f(1)+f′(1)(x−1) =x−1,\\[4pt]p_2(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2 = (x−1)−\dfrac{1}{2}(x−1)^2 \\[4pt]p_3(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2+\dfrac{f'''(1)}{3!}(x−1)^3=(x−1)−\dfrac{1}{2}(x−1)^2+\dfrac{1}{3}(x−1)^3 \end{align*}$$

Графіки$y=f(x)$ і перших трьох поліномів Тейлора наведені на малюнку$\PageIndex{1}$.

Малюнок$\PageIndex{1}$: Функція$y=\ln x$ та поліноми Тейлора$p_0,p_1,p_2$ та$p_3$ at$x=1$ побудовані на цьому графіку.

Вправа$\PageIndex{1}$

Знайдіть поліноми Тейлора$p_0,p_1,p_2$ і$p_3$ для$f(x)=\dfrac{1}{x^2}$ at$x=1$.

Підказка

Знайдіть перші три похідні$f$ і оцініть їх на$x=1.$

Відповідь

\ [\ почати {вирівнювати*} p_0 (x) &=1\ [5pt]
p_1 (x) &=1−2 (x−1)\\ [5pt]
p_2 (x) &=1−2 (x−1) +3 (x−1) ^2\\ [5pt]
p_3 (x) &=1−2 (x−1) +3 (x−1) ^2\ [5pt] p_3 (x) −1) ^2−4 (x−1) ^3\ end {align*}\]

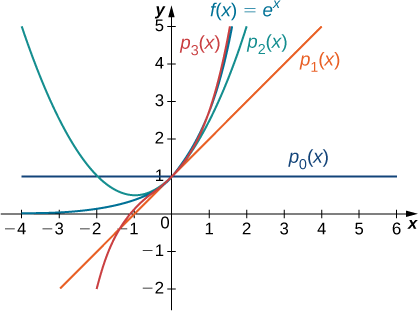
Зараз ми покажемо, як знайти поліноми Маклорена для$e^x, \sin x,$ і$\cos x$. Як зазначалося вище, поліноми Маклорена - це поліноми Тейлора, зосереджені на нулі.

Приклад$\PageIndex{2}$: Finding Maclaurin Polynomials

Для кожної з наступних функцій знайдіть формули для поліномів Маклорена$p_0,p_1,p_2$ і$p_3$. Знайдіть формулу для полінома Маклорена$n^{\text{th}}$ -ступеня і запишіть її за допомогою сигма-нотації. Використовуйте утиліту графіків для порівняння графіків$p_0,p_1,p_2$ і$p_3$ з$f$.

1. $f(x)=e^x$
2. $f(x)=\sin x$
3. $f(x)=\cos x$

Рішення

Так як$f(x)=e^x$, ми знаємо, що$f(x)=f′(x)=f''(x)=⋯=f^{(n)}(x)=e^x$ для всіх натуральних чисел$n$. Тому,

$$f(0)=f′(0)=f''(0)=⋯=f^{(n)}(0)=1 \nonumber$$

для всіх натуральних чисел$n$. Тому у нас є

\ (\ почати {вирівнювати*} p_0 (x) &= f (0) =1,\\ [
5pt] p_1 (x) &= f (0) +f′ (0) х = 1+х,\\ [5пт]
p_2 (x) &= f (0) +f (0) x+\ dfrac {f "(0)} {2} x^2=1+x+\ dfrac {1} {2} x^2,\\ [5pt]
p_3 (x) &=f (0) +f′ (0) x+\ dfrac {f "(0)} {2} x^2+\ dfrac {f"' (0)} {3!} x^3=1+x+\ dfrac {1} {2} x^2+\ dfrac {1} {3!} x^3,\ end {вирівнювати*}\)

\ (\ стиль відображення\ почати {вирівнювати*} p_n (x) &=f (0) +f′ (0) x+\ dfrac {f "(0)} {2} x^2+\ dfrac {f"' (0)} {3!} x^3++\ dfrac {f^ {(n)} (0)} {n!} x^n\\ [5pt]
&=1+х+\ dfrac {x^2} {2!} +\ dfrac {x^3} {3!} ++\ dfrac {x^n} {n!} \\ [5pt]
&=\ сума_ {k=0} ^n\ dfrac {x^k} {k!} \ end {вирівнювати*}\).

Функція і перші три поліноми Маклорена показані на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: На графіку показані функції$y=e^x$ і поліноми Маклорена$p_0,\,p_1,\,p_2$ і$p_3$.

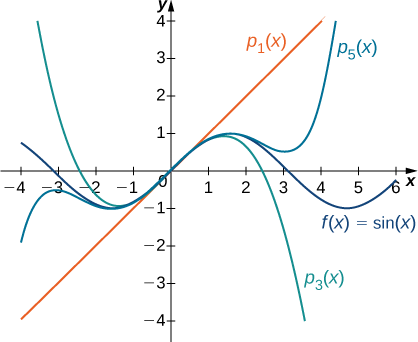
б. бо$f(x)=\sin x$, значення функції та її перших чотирьох похідних при$x=0$ наведені наступним чином:

\ [\ begin {align*} f (x) &=\ sin x & f (0) &=0\\ [5pt]
f′ (x) &=\ cos x & f′ (0) &=1\\ [5pt]
f "(x) &=−\ sin x & f" (0) &=0\\ [5pt]
f (x) &=\ cos x & f"' (0) &=−1\\ [5pt]
f^ {(4)} (x) &=\ sin x & f^ {(4)} (0) &=0. \ end {вирівнювати*}\]

Так як четверта похідна -$\sin x,$ візерунок повторюється. Тобто,$f^{(2m)}(0)=0$ і$f^{(2m+1)}(0)=(−1)^m$ для$m≥0.$ Таким чином, ми маємо

\ (\ почати {вирівнювати*} p_0 (x) &=0,\\ [
5pt] p_1 (x) &=0+х = x,\\ [
5pt] p_2 (x) &=0+x+0=x,\\ [5pt]
p_3 (x) &=0+x+0−\ dfrac {1} {3} x^3=x−\ dfrac {x^3} {3!} ,\\ [5pt]
p_4 (x) &=0+х+0−\ dfrac {1} {3!} x^3+0=x−\ dfrac {x^3} {3!} ,\\ [5pt]
p_5 (x) &=0+х+0−\ dfrac {1} {3!} x^3+0+\ dfrac {1} {5!} x^5=x−\ dfrac {x^3} {3!} +\ dfrac {x^5} {5!} ,\ end {вирівнювати*}\)

і для того$m≥0$,

\ [\ почати {вирівнювати*} p_ {2м+1} (x) =p_ {2м+2} (x) &=x−\ dfrac {x^3} {3!} +\ dfrac {x^5} {5!} −+ (−1) ^м\ dfrac {x^ {2м+1}} {(2м+1)!} \\ [5pt]
&=\ сума_ {k=0} ^м (−1) ^k\ dfrac {x^ {2k+1}} {(2к+1)!}. \ end {вирівнювати*}\]

Графіки функції та її поліномів Маклорена наведені на малюнку$\PageIndex{3}$.

Малюнок$\PageIndex{3}$: На графіку показані функції$y=\sin x$ і поліноми Маклорена$p_1,\, p_3$ і$p_5$.

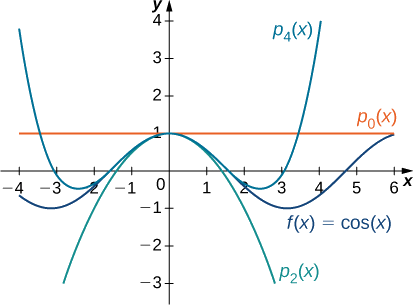
c. for$f(x)=\cos x$, значення функції та її перших чотирьох похідних при$x=0$ наведені наступним чином:

\ [\ begin {align*} f (x) &=\ cos x & f (0) &=1\\ [5pt]
f′ (x) &=−\ sin x & f′ (0) &== 0\\\ [5пт]
f "(x) &=\ cos x & f" (0) &== 1\\ [5pt]
f "(x) &=\ cos x & f" (0) &== 1\\ [5pt] f' (x) &=\ sin x & f"' (0) &=0\\ [5pt]
f^ {(4)} (x) &=\ cos x & f^ {(4)} (0) &=1. \ end {вирівнювати*}\]

Оскільки четверта похідна є$\sin x$, візерунок повторюється. Іншими словами,$f^{(2m)}(0)=(−1)^m$ і$f^{(2m+1)}=0$ для$m≥0$. Тому,

\ (\ почати {вирівнювати*} p_0 (x) &=1,\\ [5pt]
p_1 (x) &=1+0=1,\\ [5pt]
p_2 (x) &=1+0−\ dfrac {1} {2!} x^2=1−\ dfrac {x^2} {2!} ,\\ [5pt]
p_3 (x) &=1+0−\ dfrac {1} {2!} x^2+0=1−\ dfrac {x^2} {2!} ,\\ [5pt]
p_4 (x) &=1+0−\ dfrac {1} {2!} x^2+0+\ dfrac {1} {4!} x^4=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} ,\\ [5pt]
p_5 (x) &=1+0−\ dfrac {1} {2!} x^2+0+\ dfrac {1} {4!} x^4+0=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} ,\ end {вирівнювати*}\)

і для того$n≥0$,

\ [\ почати {вирівнювати*} p_ {2m} (x) &=p_ {2м+1} (x)\\ [5pt]
&=1−\ dfrac {x^2} {2!} +\ dfrac {x^4} {4!} −+ (−1) ^м\ dfrac {x^ {2m}} {(2м)!} \\ [5pt]
&=\ сума_ {k=0} ^м (−1) ^k\ dfrac {x^ {2k}} {(2k)!}. \ end {вирівнювати*}\]

Графіки функції та поліноми Маклорена представлені на рисунку$\PageIndex{4}$.

Малюнок$\PageIndex{4}$: Функція$y=\cos x$ і поліноми Маклорена$p_0,p_2$ і$p_4$ побудовані на цьому графіку.

Вправа$\PageIndex{2}$

Знайдіть формули для многочленів Маклорена$p_0,\,p_1,\,p_2$ і$p_3$ для$f(x)=\dfrac{1}{1+x}$.

Знайдіть формулу для полінома Маклорина$n^{\text{th}}$ -ступеня. Напишіть свою відповідь, використовуючи сигма-нотацію.

Підказка

Оцініть перші чотири похідні$f$ і шукайте візерунок.

Відповідь

$\displaystyle p_0(x)=1;\;p_1(x)=1−x;\;p_2(x)=1−x+x^2;\;p_3(x)=1−x+x^2−x^3;\;p_n(x)=1−x+x^2−x^3+⋯+(−1)^nx^n=\sum_{k=0}^n(−1)^kx^k$

Теорема Тейлора з залишком

Нагадаємо, що поліном Тейлора$n^{\text{th}}$ -ступеня для функції$f$ at$a$ є$n^{\text{th}}$ частковою сумою ряду Тейлора для$f$ at$a$. Тому, щоб визначити, чи сходиться ряд Тейлора, нам потрібно визначити, чи${p_n}$ сходиться послідовність поліномів Тейлора. Однак ми не тільки хочемо знати, чи сходиться послідовність поліномів Тейлора, ми хочемо знати, чи сходиться вона$f$. Щоб відповісти на це питання, визначаємо залишок$R_n(x)$ як

$$R_n(x)=f(x)−p_n(x). \nonumber$$

Щоб послідовність поліномів Тейлора сходилася до$f$, нам потрібно,$R_n$ щоб залишок зійшовся до нуля. Щоб визначити, чи$R_n$ сходиться до нуля, введемо теорему Тейлора з залишком. Ця теорема не тільки корисна для доведення того, що ряд Тейлора сходиться до його пов'язаної функції, але вона також дозволить нам кількісно оцінити, наскільки добре поліном Тейлора$n^{\text{th}}$ -ступеня наближає функцію.

Тут ми шукаємо пов'язане на$|R_n|.$ Розглянемо найпростіший випадок:$n=0$. $p_0$Дозволяти бути ^0-й поліном Тейлора at$a$ для функції$f$. Залишок$R_0$ задовольняє

$R_0(x)=f(x)−p_0(x)=f(x)−f(a).$

Якщо$f$ диференційовний на інтервалі$x$,$I$ що містить$a$ і, то за теоремою про середнє значення існує дійсне число$c$ між$a$ і$x$ таким, що$f(x)−f(a)=f′(c)(x−a)$. Тому,

$$R_0(x)=f′(c)(x−a). \nonumber$$

Використовуючи теорему про середнє значення в подібному аргументі, ми можемо показати,$f$ що якщо$n$ раз диференційовний на інтервалі,$I$ що містить$a$ і$x$, то$n^{\text{th}}$ залишок$R_n$ задовольняє

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$

для деякого реального числа$c$ між$a$ і$x$. Важливо відзначити, що значення$c$ в чисельнику вище - це не центр$a$, а скоріше невідоме значення$c$ між$a$ і$x$. Ця формула дозволяє отримати зв'язаний на залишку$R_n$. Якщо ми знаємо, що$∣f^{(n+1)}(x)∣$ обмежується деяким дійсним числом$M$ на цьому інтервалі$I$, то

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

для всіх$x$ в інтервалі$I$.

Тепер ми констатуємо теорему Тейлора, яка забезпечує формальний зв'язок між функцією$f$ та її поліномом Тейлора$n^{\text{th}}$ -ступеня$p_n(x)$. Ця теорема дозволяє зв'язати помилку при використанні полінома Тейлора для наближення значення функції, і буде важливою для доведення того, що ряд Тейлора для$f$ сходиться до$f$.

Теорема Тейлора з залишком

$f$Дозволяти функція, яка може бути диференційована$n+1$ часом на інтервалі,$I$ що містить дійсне число$a$. $p_n$Дозволяти бути$n^{\text{th}}$ -ступінь Тейлора поліном$f$ at$a$ і нехай

$$R_n(x)=f(x)−p_n(x) \nonumber$$

бути$n^{\text{th}}$ залишком. Тоді для кожного$x$ в$I$ інтервалі існує дійсне число$c$ між$a$ і$x$ таким, що

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$ .

Якщо існує дійсне число$M$ таке, що$∣f^{(n+1)}(x)∣≤M$ для всіх$x∈I$, то

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

для всіх$x$ в$I$.

Доказ

Зафіксуйте точку$x∈I$ та введіть функцію$g$ таку, що

$$g(t)=f(x)−f(t)−f′(t)(x−t)−\dfrac{f''(t)}{2!}(x−t)^2−⋯−\dfrac{f^{(n)}(t)}{n!}(x−t)^n−R_n(x)\dfrac{(x−t)^{n+1}}{(x−a)^{n+1}}. \nonumber$$

Ми стверджуємо, що$g$ задовольняє критеріям теореми Ролля. Оскільки$g$ є поліноміальною функцією (in$t$), вона є диференційованою функцією. Крім того,$g$ дорівнює нулю при$t=a$ і$t=x$ тому

$$\begin{align*} g(a) &=f(x)−f(a)−f′(a)(x−a)−\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n−R_n(x) \\[4pt] &=f(x)−p_n(x)−R_n(x) \\[4pt] &=0, \\[4pt] g(x) &=f(x)−f(x)−0−⋯−0 \\[4pt] &=0. \end{align*}$$

Тому$g$ задовольняє теорему Ролла, і, отже, існує$c$ між$a$ і$x$ такими, що$g′(c)=0.$ Ми зараз обчислюємо$g′$. Використовуючи правило продукту, відзначимо, що

$$\dfrac{d}{dt}\left[\dfrac{f^{(n)}(t)}{n!}(x−t)^n\right]=−\dfrac{f^{(n)}(t)}{(n−1)!}(x−t)^{n−1}+\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n. \nonumber$$

Отже,

\ [\ begin {вирівнювання} g′ (t) &=−f′ (t) + [f′ (t) −f "(t) (t) (x−t)] +\ left [f" (t) (x−t) −\ dfrac {f"' (t)} {2!} (x−t) ^2\ праворуч] +\ нечисло\\
&\ квадрат+\ ліворуч [\ dfrac {f^ {(n)} (t)} {(n−1)!} (x−t) ^ {n−1} −\ dfrac {f^ {(n+1)} (t)} {n!} (x−t) ^n\ праворуч] + (n+1) r_n (x)\ dfrac {(x−t) ^n} {(x−a) ^ {n+1}}\ end {вирівнювання}\ nonumber\].

Зверніть увагу, що є телескопічний ефект. Тому,

$$g'(t)=−\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n+(n+1)R_n(x)\dfrac{(x−t)^n}{(x−a)^{n+1}} \nonumber$$ .

За теоремою Ролла, ми робимо висновок, що існує число$c$ між$a$ і$x$ таким, що$g′(c)=0.$ Оскільки

$$g′(c)=−\dfrac{f^{(n+1})(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}} \nonumber$$

робимо висновок, що

$$−\dfrac{f^{(n+1)}(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}}=0. \nonumber$$

Склавши перший член з лівого боку в обидві сторони рівняння і розділивши обидві сторони рівняння,$n+1,$ зробимо висновок, що

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$

за бажанням. З цього факту випливає, що якщо існує$M$ таке, що$∣f^{(n+1)}(x)∣≤M$ для всіх$x$ в$I$, то

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$ .

□

Теорема Тейлора не тільки дозволяє довести, що ряд Тейлора сходиться до функції, але й дозволяє оцінити точність поліномів Тейлора в наближенні значень функцій. Ми починаємо з розгляду лінійних і квадратичних наближень$f(x)=\sqrt[3]{x}$ at$x=8$ і визначаємо, наскільки точні ці наближення при оцінці$\sqrt[3]{11}$.

Приклад$\PageIndex{3}$: Using Linear and Quadratic Approximations to Estimate Function Values

Розглянемо функцію$f(x)=\sqrt[3]{x}$.

1. Знайдіть перший і другий многочлени Тейлора для$f$ at$x=8$. Використовуйте утиліту графіків, щоб порівняти ці поліноми з$f$ близькими$x=8.$
2. Використовуйте ці два поліноми для оцінки$\sqrt[3]{11}$.
3. Використовуйте теорему Тейлора, щоб зв'язати помилку.

Рішення:

а Для$f(x)=\sqrt[3]{x}$, значення функції та її перших двох$x=8$ похідних при наступні:

\ [\ почати {вирівнювати*} f (x) &=\ sqrt [3] {x}, & f (8) &= 2\\ [5pt]
f′ (x) &=\ dfrac {1} {3x^ {2/3}}, & f′ (8) &=\ dfrac {1} {12}\ [5pt] f "(x) &=\ dfrac {1} {12}\ [5pt]
f" (x) &=\ dfrac {1} frac {−2} {9x^ {5/3}}, & f "(8) &=−\ dfrac {1} {144.} \ end {вирівнювати*}\]

Таким чином, перший і другий поліноми Тейлора при$x=8$ задаються

\ (\ почати {вирівнювати*} p_1 (x) &=f (8) +f′ (8) (x−8)\\ [5pt]
&=2+\ dfrac {1} {12} (x−8)\ end {align*}\)

\ (\ begin {align*} p_2 (x) &=f (8) +f′ (8) (x−8) +\ dfrac {f "(8)} {2!} (x−8) ^2\ [5pt]
&=2+\ dfrac {1} {12} (x−8) −\ dfrac {1} {288} (x−8) ^2. \ end {вирівнювати*}\)

Функція і поліноми Тейлора показані на малюнку$\PageIndex{5}$.

Малюнок$\PageIndex{5}$: Графіки$f(x)=\sqrt[3]{x}$ і лінійні і квадратичні наближень$p_1(x)$ і$p_2(x)$

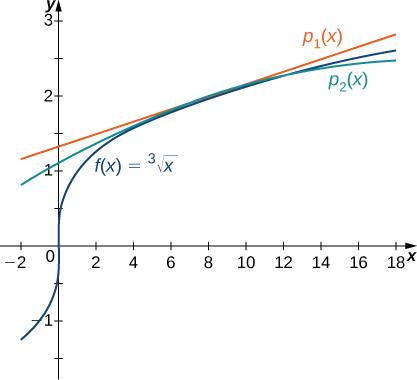
b Використовуючи перший поліном Тейлора at$x=8$, ми можемо оцінити

$$\sqrt[3]{11}≈p_1(11)=2+\dfrac{1}{12}(11−8)=2.25. \nonumber$$

Використовуючи другий многочлен Тейлора at$x=8$, отримуємо

$$\sqrt[3]{11}≈p_2(11)=2+\dfrac{1}{12}(11−8)−\dfrac{1}{288}(11−8)^2=2.21875. \nonumber$$

c Примітка, існує c в інтервалі$(8,11)$ такий, що залишок при наближенні$\sqrt[3]{11}$ першим поліномом Тейлора задовольняє

$$R_1(11)=\dfrac{f''(c)}{2!}(11−8)^2. \nonumber$$

Ми не знаємо точного значення$c,$ тому знаходимо верхню межу,$R_1(11)$ визначаючи максимальне значення$f''$ на інтервалі$(8,11)$. Так як$f''(x)=−\dfrac{2}{9x^{5/3}}$, найбільше значення для$|f''(x)|$ на цьому інтервалі відбувається при$x=8$. Використовуючи те$f''(8)=−\dfrac{1}{144}$, що, отримуємо

$|R_1(11)|≤\dfrac{1}{144⋅2!}(11−8)^2=0.03125.$

Аналогічно для оцінки$R_2(11)$ використовуємо той факт, що

$R_2(11)=\dfrac{f'''(c)}{3!}(11−8)^3$.

Так як$f'''(x)=\dfrac{10}{27x^{8/3}}$, максимальне значення$f'''$ на інтервалі$(8,11)$ дорівнює$f'''(8)≈0.0014468$. Тому у нас є

$|R_2(11)|≤\dfrac{0.0011468}{3!}(11−8)^3≈0.0065104.$

Вправа$\PageIndex{3}$:

Знайдіть перший і другий многочлени Тейлора для$f(x)=\sqrt{x}$ at$x=4$. Використовуйте ці многочлени для оцінки$\sqrt{6}$. Використовуйте теорему Тейлора, щоб зв'язати помилку.

Підказка

Оцініть$f(4),f′(4),$ і$f''(4).$

Відповідь

$p_1(x)=2+\dfrac{1}{4}(x−4);p_2(x)=2+\dfrac{1}{4}(x−4)−\dfrac{1}{64}(x−4)^2;p_1(6)=2.5;p_2(6)=2.4375;$

$|R_1(6)|≤0.0625;|R_2(6)|≤0.015625$

Приклад$\PageIndex{4}$: Approximating $\sin x$ Using Maclaurin Polynomials

З прикладу$\PageIndex{2b}$, поліноми Маклорена для$\sin x$ задаються

$$p_{2m+1}(x)=p_{2m+2}(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!}−\dfrac{x^7}{7!}+⋯+(−1)^m\dfrac{x^{2m+1}}{(2m+1)!} \nonumber$$

для$m=0,1,2,….$

1. Використовуйте п'ятий поліном Маклорена для$\sin x$ наближення$\sin\left(\dfrac{π}{18}\right)$ та зв'язування похибки.
2. Для яких значень$x$ робить п'ятий поліном Маклорена наближений$\sin x$ до всередині$0.0001$?

Рішення

а.

П'ятий многочлен Маклорина - це

$$p_5(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!} \nonumber$$ .

Використовуючи цей многочлен, ми можемо оцінити наступним чином:

$$\sin\left(\dfrac{π}{18}\right)≈p_5\left(\dfrac{π}{18}\right)=\dfrac{π}{18}−\dfrac{1}{3!}\left(\dfrac{π}{18}\right)^3+\dfrac{1}{5!}\left(\dfrac{π}{18}\right)^5≈0.173648. \nonumber$$

Щоб оцінити похибку, використовують той факт, що шостий поліном Маклорена є$p_6(x)=p_5(x)$ і обчислити пов'язане на$R_6(\dfrac{π}{18})$. За Приміткою, залишок дорівнює

$$R_6\left(\dfrac{π}{18}\right)=\dfrac{f^{(7)}(c)}{7!}\left(\dfrac{π}{18}\right)^7 \nonumber$$

для деяких$c$ між 0 і$\dfrac{π}{18}$. Використовуючи той факт, що$∣f^{(7)}(x)∣≤1$ для всіх$x$, ми знаходимо, що величина похибки становить максимум

$$\dfrac{1}{7!}⋅\left(\dfrac{π}{18}\right)^7≤9.8×10^{−10}. \nonumber$$

б.

Нам потрібно знайти значення$x$ таких, що

$$\dfrac{1}{7!}|x|^7≤0.0001. \nonumber$$

Вирішуючи цю нерівність для$x$, ми маємо, що п'ятий поліном Маклорена дає оцінку в межах до тих$0.0001$ пір, поки$|x|<0.907.$

Вправа$\PageIndex{4}$

Використовуйте четвертий многочлен Маклорена для$\cos x$ наближення$\cos\left(\dfrac{π}{12}\right).$

Підказка

Четвертий многочлен Маклорина - це$p_4(x)=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!}$.

Відповідь

0.96593

Тепер, коли ми можемо зв'язати решту$R_n(x)$, ми можемо використовувати це пов'язане, щоб довести, що серія Тейлора для$f$ at сходиться до$f$.

Представлення функцій з серіями Тейлора та Маклоріна

Зараз ми обговорюємо питання конвергенції для серії Тейлора. Почнемо з того, що показуємо, як знайти ряд Тейлора для функції та як знайти її інтервал збіжності.

Приклад$\PageIndex{5}$: Finding a Taylor Series

Знайдіть серію Тейлора для$f(x)=\dfrac{1}{x}$ at$x=1$. Визначте інтервал збіжності.

Рішення

Для$f(x)=\dfrac{1}{x},$ значень функції та її перших чотирьох$x=1$ похідних at

\ [\ почати {вирівнювати*} f (x) &=\ dfrac {1} {x} & f (1) &=1\\ [5pt]
f′ (x) &=−\ dfrac {1} {x^2} & f′ (1) &=−1\\ [5pt]
f "(x) &=\ dfrac {2} {x^3} f" (1) &=2! \\ [5pt]
f"' (x) &=−\ dfrac {3⋅2} {x^4} & f"' (1) &=−3! \\ [5pt]
f^ {(4)} (x) &=\ dfrac {4⋅3⋅2} {x^5} & f^ {(4)} (1) &=4!. \ end {вирівнювати*}\]

Тобто у нас є$f^{(n)}(1)=(−1)^nn!$ для всіх$n≥0$. Тому серіал Тейлора для$f$ at$x=1$ дається

$\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(1)}{n!}(x−1)^n=\sum_{n=0}^∞(−1)^n(x−1)^n$.

Щоб знайти інтервал збіжності, скористаємося тестом співвідношення. Ми знаходимо, що

$\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{∣(−1)^{n+1}(x−1)n^{+1}∣}{|(−1)^n(x−1)^n|}=|x−1|$.

Таким чином, ряд сходиться, якщо$|x−1|<1.$ Тобто, ряд сходиться для$0<x<2$. Далі нам потрібно перевірити кінцеві точки. На$x=2$, ми бачимо, що

$\displaystyle \sum_{n=0}^∞(−1)^n(2−1)^n=\sum_{n=0}^∞(−1)^n$

розходиться по тесту на дивергенцію. Аналогічно при$x=0,$

$\displaystyle \sum_{n=0}^∞(−1)^n(0−1)^n=\sum_{n=0}^∞(−1)^{2n}=\sum_{n=0}^∞1$

розходиться. Тому інтервал зближення є$(0,2)$.

Вправа$\PageIndex{5}$

Знайдіть ряд Тейлора для$f(x)=\dfrac{1}{2}$ at$x=2$ і визначте його інтервал збіжності.

Підказка

$f^{(n)}(2)=\dfrac{(−1)^nn!}{2^{n+1}}$

Відповідь

$\dfrac{1}{2}\displaystyle \sum_{n=0}^∞\left(\dfrac{2−x}{2}\right)^n$. Інтервал зближення дорівнює$(0,4)$.

Ми знаємо, що серія Тейлора, знайдена в цьому прикладі, сходиться на інтервалі$(0,2)$, але як ми знаємо, що вона насправді сходиться до$f$? Розглянемо це питання більш узагальнено за мить, але для цього прикладу ми можемо відповісти на це питання, написавши

$$f(x)=\dfrac{1}{x}=\dfrac{1}{1−(1−x)}. \nonumber$$

Тобто$f$ може бути представлений геометричним рядом$\displaystyle \sum_{n=0}^∞(1−x)^n$. Оскільки це геометричний ряд, він сходиться до тих$\dfrac{1}{x}$ пір, поки$|1−x|<1.$ Тому серія Тейлора, знайдена в Прикладі, сходиться до$f(x)=\dfrac{1}{x}$$(0,2).$

Тепер ми розглянемо більш загальне питання: якщо ряд Тейлора для функції$f$ сходиться на деякому інтервалі, як ми можемо визначити, чи дійсно він сходиться до$f$? Щоб відповісти на це питання, нагадаємо, що ряд сходиться до певного значення тоді і тільки тоді, коли його послідовність часткових сум сходиться до цього значення. Враховуючи ряд Тейлора для$f$ at$a$,$n^{\text{th}}$ часткова сума задається$n^{\text{th}}$ поліномом Тейлора -ступеня$p_n$. Тому, щоб визначити, чи сходиться ряд Тейлора до$f$, нам потрібно визначити, чи

$\displaystyle \lim_{n→∞}p_n(x)=f(x)$.

Оскільки решта$R_n(x)=f(x)−p_n(x)$, серія Тейлора сходиться до$f$ якщо і тільки тоді

$\displaystyle \lim_{n→∞}R_n(x)=0.$

Зараз ми викладати цю теорему формально.

Конвергенція серії Тейлора

Припустимо, що$f$ має похідні всіх замовлень на інтервалі,$I$ що містять$a$. Тоді серіал Тейлора

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n \nonumber$$

сходиться до$f(x)$ для всіх$x$ в$I$ якщо і тільки якщо

$$\lim_{n→∞}R_n(x)=0 \nonumber$$

для всіх$x$ в$I$.

За допомогою цієї теореми ми можемо довести, що ряд Тейлора для$f$ at a сходиться до того,$f$ якщо ми можемо довести, що залишок$R_n(x)→0$. Щоб довести це$R_n(x)→0$, ми зазвичай використовуємо bound

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

з теореми Тейлора з залишком.

У наступному прикладі ми знаходимо ряд Маклорена for$e^x$$\sin x$ і показуємо, що ці ряди сходяться з відповідними функціями для всіх дійсних чисел, доводячи, що залишки$R_n(x)→0$ для всіх дійсних чисел$x$.

Приклад$\PageIndex{6}$: Finding Maclaurin Series

Для кожної з наступних функцій знайдіть ряд Маклорена і його інтервал збіжності. Використовуйте Примітку, щоб довести, що ряд Маклорена для$f$ збігається$f$ на цьому інтервалі.

1. $e^x$
2. $\sin x$

Рішення

а Використовуючи поліном Маклорена$n^{\text{th}}$ -ступеня для$e^x$ знайденого в прикладі a., ми виявимо, що ряд Маклорена для$e^x$ задається

$\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}$.

Для визначення інтервалу збіжності скористаємося тестом коефіцієнта. Так як

$\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{|x|^{n+1}}{(n+1)!}⋅\dfrac{n!}{|x|^n}=\dfrac{|x|}{n+1}$,

у нас є

$\displaystyle \lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=\lim_{n→∞}\dfrac{|x|}{n+1}=0$

для всіх$x$. Тому ряд сходиться абсолютно для всіх$x$, і, таким чином, інтервал зближення є$(−∞,∞)$. Щоб показати, що ряд сходиться до$e^x$ для всіх$x$, ми використовуємо той факт, що$f^{(n)}(x)=e^x$ для всіх$n≥0$ і$e^x$ є зростаючою функцією на$(−∞,∞)$. Тому для будь-якого дійсного числа$b$ максимальне значення$e^x$ для всіх$|x|≤b$ дорівнює$e^b$. Таким чином,

$|R_n(x)|≤\dfrac{e^b}{(n+1)!}|x|^{n+1}$.

Оскільки ми тільки що показали, що

$\displaystyle \sum_{n=0}^∞\dfrac{|x|^n}{n!}$

сходиться для всіх$x$, за тестом на розбіжність, ми знаємо, що

$\displaystyle \lim_{n→∞}\dfrac{|x|^{n+1}}{(n+1)!}=0$

для будь-якого дійсного числа$x$. Поєднавши цей факт з теоремою стискання, результат$\displaystyle \lim_{n→∞}R_n(x)=0.$

b Використовуючи поліном Маклорена$n^{\text{th}}$ -ступеня для$\sin x$ знайденого в прикладі b., ми виявимо, що ряд Маклорена для$\sin x$ задається

$\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}$.

Для того, щоб застосувати тест співвідношення, розглянемо

\ [\ почати {вирівнювати*}\ dfrac {|a_ {n+1} |} {|a_n|} &=\ dfrac {|x|^ {2n+3}} {(2n+3)!} ⋅\ фрак {(2n+1)!} {|x|^ {2n+1}}\\ [5pt]
&=\ dfrac {|x|^2} {(2n+3) (2n+2)}\ кінець {вирівнювати*}. \ номер\]

Так як

$\displaystyle \lim_{n→∞}\dfrac{|x|^2}{(2n+3)(2n+2)}=0$

для всіх$x$ ми отримуємо інтервал збіжності як$(−∞,∞).$ Щоб показати, що ряд Маклорена сходиться до$\sin x$, подивіться на$R_n(x)$. Для кожного$x$ існує дійсне число$c$ між$0$ і$x$ таким, що

$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}x^{n+1}$.

Оскільки$∣f^{(n+1)}(c)∣≤1$ для всіх цілих чисел$n$ і всіх дійсних чисел $c$, у нас є

$|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}$

для всіх дійсних чисел$x$. Використовуючи ту ж ідею, що і в частині а., результат$\displaystyle \lim_{n→∞}R_n(x)=0$ для всіх$x$, а отже, серія Маклорена для$\sin x$ сходиться до$\sin x$ для всіх реальних$x$.

Вправа$\PageIndex{6}$

Знайдіть серію Маклорен для$f(x)=\cos x$. Використовуйте тест співвідношення, щоб показати, що інтервал збіжності є$(−∞,∞)$. Показати, що ряд Маклорена сходиться до$\cos x$ для всіх дійсних чисел$x$.

Підказка

Використовуйте многочлени Маклорина для$\cos x.$

Відповідь

$\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{2n}}{(2n)!}$

За тестом співвідношення інтервал збіжності дорівнює$(−∞,∞).$ Так$|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}$, ряд сходиться до$\cos x$ для всіх реальних$x$.

Доводячи, що$e$ is Irrational

У цьому проекті ми використовуємо поліноми Маклорена для того,$e^x$ щоб довести, що$e$ це ірраціонально. Доказ спирається на припущення, що$e$ є раціональним і доходить до протиріччя. Тому в наступних кроках ми припускаємо$e=r/s$ для деяких цілих чисел$r$ і$s$ де$s≠0.$

1. Напишіть многочлени Маклорина$p_0(x),p_1(x),p_2(x),p_3(x),p_4(x)$ для$e^x$. Оцініть$p_0(1),p_1(1),p_2(1),p_3(1),p_4(1)$, щоб оцінити$e$.
2. Нехай$R_n(x)$ позначають залишок при використанні$p_n(x)$ для оцінки$e^x$. Тому$R_n(x)=e^x−p_n(x)$, і$R_n(1)=e−p_n(1)$. Припускаючи, що$e=\dfrac{r}{s}$ для цілих чисел$r$ і$s$, оцінити$R_0(1),R_1(1),R_2(1),R_3(1),R_4(1).$
3. Використовуючи результати з частини 2, показати, що для кожного залишку$R_0(1),R_1(1),R_2(1),R_3(1),R_4(1),$ ми можемо знайти ціле число,$k$ яке$kR_n(1)$ є цілим числом для$n=0,1,2,3,4.$
4. Запишіть формулу для$n^{\text{th}}$ -градусного полінома Маклорена$p_n(x)$ для$e^x$ і відповідного залишку$R_n(x).$ Показати, що$sn!R_n(1)$ є цілим числом.
5. Використовуйте теорему Тейлора, щоб записати явну формулу для$R_n(1)$. Зробіть висновок$R_n(1)≠0$, що, і, отже,$sn!R_n(1)≠0$.
6. Використовуйте теорему Тейлора, щоб знайти оцінку на$R_n(1)$. Використовуйте цю оцінку в поєднанні з результатом частини 5, щоб показати це$|sn!R_n(1)|<\dfrac{se}{n+1}$. Зробіть висновок,$n$ що якщо досить великий, то$|sn!R_n(1)|<1$. Отже,$sn!R_n(1)$ є цілим числом з величиною менше 1. Таким чином,$sn!R_n(1)=0$. Але з частини 5 ми це знаємо$sn!R_n(1)≠0$. Ми дійшли до протиріччя, і, отже, початкове припущення про те, що e є раціональним, має бути помилковим.

Ключові поняття

• Поліноми Тейлора використовуються для наближення функцій поблизу значення$x=a$. Поліноми Маклорина - це поліноми Тейлора на$x=0$.
• Поліноми Тейлора$n^{\text{th}}$ -ступеня для функції$f$ є частковими сумами ряду Тейлора для$f$.
• Якщо функція$f$ має представлення степеневого ряду в$x=a$, то вона задається її серією Тейлора в$x=a$.
• Серія Тейлора для$f$ сходиться$f$ якщо і тільки якщо$\displaystyle \lim_{n→∞}R_n(x)=0$ де$R_n(x)=f(x)−p_n(x)$.
• Серія Тейлора для$e^x, \sin x$ та$\cos x$ зближення до відповідних функцій для всіх реальних x.

Ключові рівняння

• Серія Тейлора для функції$f$ в точці$x=a$

$\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯$

Глосарій

многочлен Маклорина

поліном Тейлора з центром$0$; поліном Тейлора для$f$ at$0$$n^{\text{th}}$ - градусний поліном Маклорена для$n^{\text{th}}$$f$

Серія Маклорен

Серія Тейлора для функції$f$ в$x=0$ відомий як серія Маклорена для$f$

Поліноми Тейлора

поліном Тейлора$n^{\text{th}}$ -ступеня для$f$ at$x=a$ є$p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n$

Серія Тейлора

силовий ряд при цьому$a$ сходиться до функції$f$ на деякому відкритому інтервалі, що містить$a$.

Теорема Тейлора з залишком

для функції$f$ та полінома Тейлора$n^{\text{th}}$ -ступеня для$f$ at$x=a$, залишок$R_n(x)=f(x)−p_n(x)$ задовольняє$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1}$

для деяких$c$ між$x$ і$a$; якщо існує інтервал,$I$ що містить$a$ і дійсне число$M$ таке, що$∣f^{(n+1)}(x)∣≤M$ для всіх$x$ в$I$, то$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1}$