6.2: Інтеграція частинами

Last updated
Save as PDF

Page ID: 60784

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ось простий інтеграл, який ми ще не можемо оцінити:

$\ int х\ cos х\, дх.\]

Це проста справа, щоб взяти похідну від integrand, використовуючи Правило продукту, але немає правила продукту для інтегралів. Однак у цьому розділі представлено Інтеграція частинами, метод інтеграції, який базується на Правилі продукту для похідних. Це дасть нам можливість оцінити цей інтеграл.

Правило продукту говорить, що якщо$u$ і$v$ є функціями$x$, то$(uv)' = u'v + uv'$. Для простоти ми написали$u$ для$u(x)$ і$v$ для$v(x)$. Припустимо, ми інтегруємо обидві сторони щодо$x$. Це дає

$\ int (ув) '\, дх =\ int (u'v+uv')\, дх.\]

За фундаментальною теоремою обчислення ліва сторона інтегрується в$uv$. Права сторона може бути розбита на два інтеграли, і у нас є

$ $ ув =\ int у'в\, ДХ +\ int ув'\, дх.\]

Рішення для другого інтеграла ми маємо

$\ int ув'\, дх = ув -\ int у'в\, дх.\]

Використовуючи диференціальні позначення, ми можемо записати$du = u'(x)dx$$dv=v'(x)dx$ і вираз вище можна записати наступним чином:

$\ int u\, dv = ув -\ int v\, ду.\]

Це формула Інтеграція по частинам. Для довідкових цілей ми констатуємо це в теоремі.

Теорема$\PageIndex{1}$: Integration by Parts

$v$Дозволяти$u$ і бути диференційовні функції$x$ на інтервалі,$I$ що містить$a$ і$b$. Тоді

\[\int u\ dv = uv - \int v\ du,\]

та інтеграція частинами

\[\int_{x=a}^{x=b} u\ dv = uv\Big|_a^b - \int_{x=a}^{x=b}v\ du.\]

Спробуємо приклад, щоб зрозуміти нашу нову техніку.

Приклад$\PageIndex{1}$: Integrating using Integration by Parts

Оцінити$\displaystyle \int x\cos{x}\ dx$.

Рішення

Ключем до інтеграції частинами є ідентифікація частини інтегралу як "$u$" і частина як "$dv$. Регулярна практика допоможе зробити хороші ідентифікації, а пізніше ми представимо деякі принципи, які допомагають. А поки нехай$u=x$ і$dv=\cos{x}\ dx$.

Як правило, корисно скласти невелику таблицю цих значень, як це робиться нижче. Зараз ми знаємо лише$u$ і$dv$ як показано зліва на малюнку$\PageIndex{1}$; праворуч ми заповнюємо решту того, що нам потрібно. Якщо$u = x$, то$du = dx$. Так як$dv = \cos x\ dx$,$v$ є антипохідним від$\cos x$. Вибираємо$v = \sin x$.

$альт$

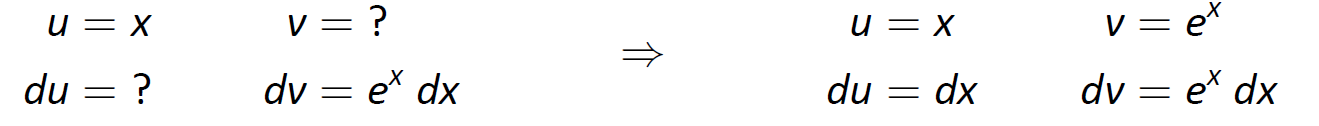
Малюнок$\PageIndex{1}$: Налаштування інтеграції по частинам.

Тепер замініть все це у формулу Інтеграція частинами, даючи

$\ int х\ cos х\, дх = х\ гріх х -\ int\ sin х\, дх.\]

Потім ми можемо$\sin x$ інтегруватися, щоб отримати$-\cos x + C$ і загалом наша відповідь

$\ int х\ cos х\ dx = х\ гріх х +\ cos х + C\]

Зверніть увагу, як антидериватив містить продукт,$x\sin x$. Цей продукт - це те, що робить інтеграцію частинами необхідною.

Наведений вище приклад демонструє, як взагалі працює інтеграція по частинам. Ми намагаємося ідентифікувати$u$ і$dv$ в інтегралі нам дано, і ключовим є те, що ми зазвичай хочемо вибрати,$u$ і$dv$ так що$du$ це простіше, ніж$u$ і$v$, сподіваюся, не надто складніше, ніж$dv$. Це означатиме, що інтеграл на правій стороні формули Інтеграція частинами$\int v\,du$ буде простіше інтегрувати, ніж оригінальний інтеграл$\int u\,dv$.

У наведеному вище прикладі ми вибрали$u=x$ і$dv=\cos x\,dx$. Тоді$du=dx$ було простіше,$v=\sin x$ ніж$u$ і не складніше$dv$. Тому замість інтеграції$x\cos x \,dx$ ми могли б інтегрувати$\sin x\,dx$, що ми вміли робити.

Корисна мнемоніка для допомоги у визначенні$u$ - «LIATE», де

\[L = \textbf{L}ogarithmic, I = \textbf{I}nverse Trig., A = \textbf{A}lgebraic (polynomials),\]

\[T = \textbf{T}rigonometric, and E = \textbf{E}xponential.\]

Якщо integrand містить як логарифмічний, так і алгебраїчний термін, загалом дозволяючи$u$ бути логарифмічний термін працює найкраще, як вказує L, що йде перед A в LIATE.

Розглянемо тепер ще один приклад.

Приклад$\PageIndex{2}$: Integrating using Integration by Parts

Оцінити$\displaystyle \int x e^x\,dx$.

Рішення

Ціле число містить алгебраїчний термін A ($x$) і\ textbf {E} експоненційний термін ($e^x$). Наша мнемоніка пропонує дозволити$u$ бути алгебраїчним терміном, тому ми вибираємо$u=x$ і$dv=e^x\,dx$. Потім$du=dx$ і$v=e^x$ як зазначено в таблицях нижче.

$альт$

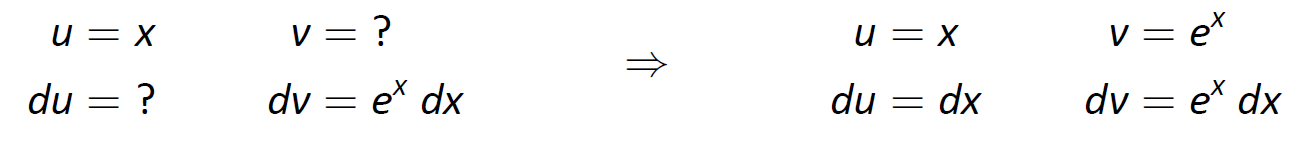
Малюнок$\PageIndex{2}$: Налаштування інтеграції по частинам.

Ми бачимо$du$ простіше$u$, ніж, поки немає змін у переході від$dv$ до$v$. Це добре. Формула інтеграції по частинам дає

$\ int х е^х\, дх = х ^ х -\ int е^х\, дх.\]

Інтеграл праворуч простий; наша остаточна відповідь

$\ int xe^x\ dx = xe^x - е ^ х + С.\]

Зверніть увагу ще раз, як антипохідні містять термін продукту.

Приклад$\PageIndex{3}$: Integrating using Integration by Parts

Оцінити$\displaystyle \int x^2\cos x \,dx$.

Рішення

Мнемоніка пропонує дозволити$u=x^2$ замість тригонометричної функції, отже$dv=\cos x\,dx$. Потім$du=2x\,dx$ і$v=\sin x$ як показано нижче.

$альт$

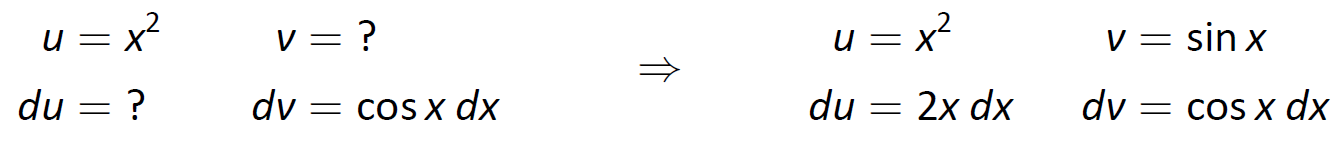
Малюнок$\PageIndex{3}$: Налаштування інтеграції по частинам.

Формула інтеграції по частинам дає

$\ int х ^ 2\ cos х\, дх = х ^ 2\ гріх х -\ int 2x\ гріх х\, дх.\]

На даний момент інтеграл праворуч дійсно простіший, ніж той, з якого ми почали, але щоб оцінити його, нам потрібно знову зробити інтеграцію частинами. Тут вибираємо$u=2x$$dv=\sin x$ і заповнюємо інші нижче.

$альт$

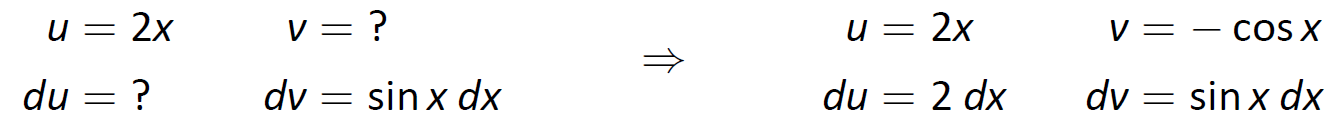
Малюнок$\PageIndex{4}$: Налаштування інтеграції по частинам.

Інтеграл весь шлях праворуч тепер те, що ми можемо оцінити. Він оцінює до$-2\sin{x}$. Потім, пройшовши і спрощуючи, будьте обережні, щоб тримати всі знаки прямо, наша відповідь
$$\ int x^2\ cos x\ dx = x^2\ sin x + 2x\ cos x - 2\ sin x + C\]

Приклад$\PageIndex{4}$: Integrating using Integration by Parts

Оцінити$\displaystyle \int e^x\cos x \,dx$.

Рішення

Це класична проблема. Наша мнемоніка пропонує$u$ дозволити тригонометричну функцію замість експоненціальної. У цьому конкретному прикладі можна дозволити$u$ бути$\cos x$ або$e^x$; щоб продемонструвати, що ми не повинні слідувати LIATE, ми вибираємо$u=e^x$ і, отже,$dv = \cos x\,dx$. Потім$du=e^x\,dx$ і$v=\sin x$ як показано нижче.

$альт$

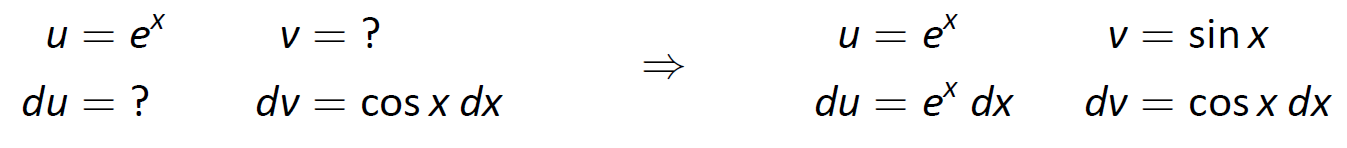
Малюнок$\PageIndex{5}$: Налаштування інтеграції по частинам.

Зверніть увагу, що$du$ це не простіше$u$, ніж, йдучи проти нашого загального правила (але несіть з нами). Формула інтеграції по частинам дає

$\ int e^x\ cos х\ dx = е ^ х\ гріх х -\ int e^x\ гріх х\, дх.\]

Інтеграл праворуч не сильно відрізняється від того, з якого ми почали, тому здається, що ми нікуди не дісталися. Давайте продовжимо працювати і застосовувати інтеграцію частинами до нового інтегралу, використовуючи$u=e^x$ і$dv = \sin x\,dx$. Це призводить нас до наступного:

$альт$

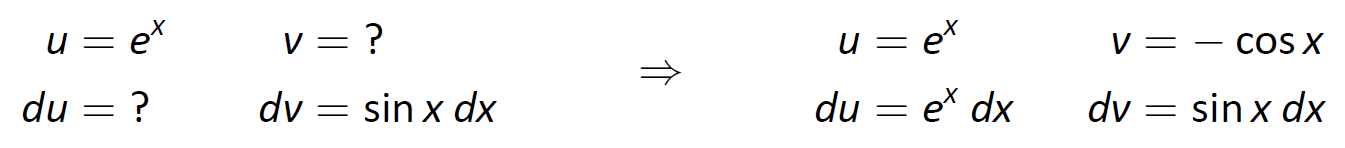
Малюнок$\PageIndex{6}$: Налаштування інтеграції по частинам.

Формула інтеграції по частинам дає:

\[\begin{align*} \int e^x\cos x\,dx &= e^x\sin x - \left(-e^x\cos x - \int -e^x\cos x\,dx\right)\\ &= e^x\sin x+ e^x\cos x - \int e^x\cos x\ dx.\end{align*}\]

Здається, ми повернулися прямо там, де ми почали, як правий бік містить$\int e^x\cos x\,dx$. Але це насправді хороша річ.

Додайте$\int e^x\cos x\ dx$ в обидві сторони. Це дає

\ [\ begin {align*} 2\ int e^x\ cos x\ dx & = e ^ x\ sin x + e^x\ cos x\ cos x\\ text {Тепер розділіть обидві сторони на 2:}
\ int e^x\ cos x\ cos x\ dx & =\ frac {1} {2}\ великий (e^x\ sin x + e^x\ cos x\ big). \ end {вирівнювати*}\]

Трохи спрощуючи і додаючи константу інтеграції, наша відповідь таким чином

$\ int e^x\ cos х\ dx =\ frac12e^x\ ліворуч (\ sin x +\ cos х\ праворуч) +C.\]

Приклад$\PageIndex{5}$: Integrating using Integration by Parts: antiderivative of $\ln x$

Оцінити$\displaystyle \int \ln x\,dx$.

Рішення

Можна було помітити, що у нас є правила інтеграції звичних тригонометричних функцій і$e^x$, але ми поки не дали правила інтеграції$\ln x$. Це тому, що не$\ln x$ може бути легко інтегрований з будь-яким із правил, які ми вивчили до цього моменту. Але ми можемо знайти його антипохідне за допомогою розумного застосування Інтеграція частинами. Набір$u=\ln x$ і$dv=dx$. Це хороший, підлий трюк, щоб навчитися, оскільки це може допомогти в інших ситуаціях. Це визначає$du=(1/x)\,dx$ і$v=x$, як показано нижче.

$альт$

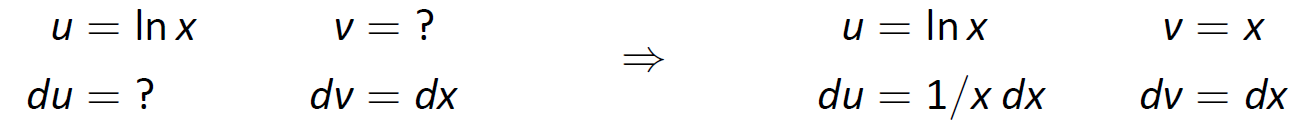
Малюнок$\PageIndex{7}$: Налаштування інтеграції по частинам.

Поклавши це все разом у формулу Інтеграція частинами, все працює дуже красиво:

$\ int\ ln х\, дх = х\ ln х -\ int х\,\ frac1x\, дх.\]

Новий інтеграл спрощує$\int 1\,dx$, який приблизно так само просто, як речі отримати. Його невід'ємною частиною є$x+C$ і наша відповідь

$\ int\ ln х\ дх = х\ ln {х} - х + С\]

Приклад$\PageIndex{6}$: Integrating using Int. by Parts: antiderivative of $\arctan x$

Оцінити$\displaystyle \int \arctan x \,dx$.

Рішення

Той самий підлий трюк, який ми використовували вище, працює тут. Нехай$u=\arctan x$ і$dv=dx$. Потім$du=1/(1+x^2)\,dx$ і$v=x$. Формула інтеграції по частинам дає

\[\int \arctan x \,dx = x\arctan x - \int \frac x{1+x^2}\,dx.\]

Інтеграл справа може бути вирішений шляхом підміни. Взявши$u=1+x^2$, отримуємо$du=2x\,dx$. Інтеграл тоді стає

\[\int \arctan x \,dx = x\arctan x - \frac12\int \frac 1{u}\,du.\]

Інтеграл на право оцінює до$\ln|u|+C$, який стає$\ln(1+x^2)+C$. Тому відповідь така

\[\int \arctan x\ dx = x\arctan x - \ln(1+x^2) + C.\]

Заміна перед інтеграцією

При прийомі похідних було прийнято використовувати кілька правил (наприклад, використання як коефіцієнтів, так і правил ланцюга). Тоді не дивно, що деякі інтеграли найкраще оцінюються, поєднуючи методи інтеграції. Зокрема, тут ми проілюструємо створення «незвичайної» заміни спочатку перед використанням Integration by Parts.

Приклад$\PageIndex{7}$: Integration by Parts after substitution

Оцінити$\displaystyle \int \cos(\ln x)\ dx$.

Рішення

Integrand містить склад функцій, що змушує нас думати, що заміщення було б корисним. Відпускаючи$u=\ln x$, у нас є$du = 1/x\ dx$. Це здається проблематичним, оскільки ми не маємо$1/x$ в цілісності. Але врахуйте:

\[du = \frac 1x\ dx \Rightarrow x\cdot du = dx.\]

Так як$u = \ln x$, ми можемо використовувати зворотні функції і зробити висновок про це$x = e^u$. Тому ми маємо це

\[\begin{align*} dx &= x\cdot du \\ &= e^u\ du.\end{align*}\]

Таким чином, ми можемо$\ln x$ замінити на$u$ і$dx$ з$e^u\ du$. Таким чином, ми перепишемо наш інтеграл як

\[\int \cos(\ln x)\ dx = \int e^u\cos u \ du.\]

Ми оцінили цей інтеграл у прикладі$\PageIndex{4}$. Використовуючи результат там, ми маємо:

\[\begin{align*}\int \cos(\ln x)\ dx &= \int e^u\cos u \ du \\ &= \frac12e^u\big(\sin u + \cos u\big) + C \\&= \frac12e^{\ln x} \big(\sin(\ln x) + \cos (\ln x)\big)+C\\ &= \frac12x \big(\sin(\ln x) + \cos (\ln x)\big)+C.\end{align*}\]

Певні інтеграли та інтеграція по частинам

Поки ми зосередилися лише на оцінці невизначеного інтегралу. Звичайно, ми можемо використовувати Інтеграцію частинами для оцінки певних інтегралів, а також$\PageIndex{1}$ теореми. Ми робимо це в наступному прикладі.

Приклад$\PageIndex{8}$: Definite integration using Integration by Parts

Оцінити$\displaystyle \int_1^2 x^2 \ln x \,dx$.

Рішення

Наша мнемоніка пропонує дозволити$u=\ln x$, отже$dv =x^2\,dx$.

Потім отримуємо$du = (1/x)\,dx$ і$v=x^3/3$ як показано нижче.

$альт$

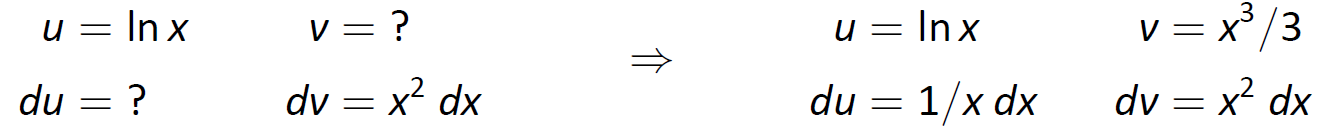
Малюнок$\PageIndex{8}$: Налаштування інтеграції по частинам.

Формула інтеграції по частинам потім дає

\[\begin{align*} \int_1^2 x^2 \ln x\,dx &= \frac{x^3}3\ln x\bigg|_1^2 - \int_1^2 \frac{x^3}{3}\,\frac 1x\,dx \\&= \frac{x^3}3\ln x\bigg|_1^2 - \int_1^2 \frac{x^2}{3}\,dx \\ &= \frac{x^3}3\ln x\bigg|_1^2 - \frac{x^3}{9}\bigg|_1^2\\&= \left(\frac{x^3}3\ln x - \frac{x^3}{9}\right)\bigg|_1^2\\ &= \left(\frac83\ln 2 - \frac89\right)-\left(\frac13\ln 1 - \frac19\right) \\ &= \frac83\ln 2 - \frac79 \\ &\approx 1.07.\end{align*}\]

Загалом, Інтеграція частинами корисна для інтеграції певних продуктів функцій, таких як$\int x e^x\,dx$ або$\int x^3\sin x\,dx$. Він також корисний для інтегралів із логарифмами та оберненими тригонометричними функціями.

Як зазначалося раніше, інтеграція, як правило, складніше, ніж деривація. Ми розробляємо інструменти для обробки великого масиву інтегралів, і досвід підкаже нам, коли один інструмент бажаний/необхідний перед іншим. Наприклад, розглянемо три аналогічні на вигляд інтеграли

$\ int xe ^ x\, x,\ qquad\ int х e^ {x^2}\, dx\ qquad\ текст {і}\ qquad\ int xe^ {x^3}\, х.\]

Хоча перший легко обчислюється за допомогою інтеграції частинами, до другого найкраще підходити із заміною. Збираючи речі на крок далі, третій інтеграл не має відповіді з точки зору елементарних функцій, тому жоден із методів, які ми вивчаємо в обчисленні, не дасть нам точної відповіді.

Інтеграція частинами є дуже корисним методом, поступаючись лише заміщенню. У наступних розділах цієї глави ми продовжуємо вивчати інші методи інтеграції. Наступний розділ присвячений обробці інтегралів, що містять тригонометричні функції.