6.1: Заміна

Попередній розділ ввів антидериватив і з'єднав його з підписаними ділянками під кривою через Фундаментальну теорему числення. Наступний розділ досліджує більше застосувань певних інтегралів, ніж просто площа. Оскільки оцінка певних інтегралів стане важливою, ми захочемо знайти антипохідні різноманітних функцій.

Ця глава присвячена дослідженню методик антидиференціації. Хоча не кожна функція має антипохідну з точки зору елементарних функцій (поняття, введене в розділі про числове інтегрування), ми все ще можемо знайти антипохідні найрізноманітніших функцій.

Заміна

Мотивуємо цей розділ прикладом. Нехай$f(x) = (x^2+3x-5)^{10}$. Ми можемо обчислити$f'(x)$ за допомогою правила ланцюга. Це:

$$f'(x) = 10(x^2+3x-5)^9\cdot(2x+3) = (20x+30)(x^2+3x-5)^9.$$

Тепер розглянемо це: Що таке$\int (20x+30)(x^2+3x-5)^9\ dx$? Перед нами відповідь;

$$\int (20x+30)(x^2+3x-5)^9\ dx = (x^2+3x-5)^{10}+C.$$

Як би ми оцінили цей невизначений інтеграл, не починаючи з того$f(x)$, як ми це зробили?

У цьому розділі розглядається інтеграція шляхом підміни. Це дозволяє нам «скасувати правило ланцюга». Заміна дозволяє оцінити вищевказаний інтеграл, не знаючи спочатку вихідної функції.

Основний принцип полягає в тому, щоб переписати «складний» інтеграл форми$\int f(x)\ dx$ як не настільки складний інтеграл$\int h(u)\ du$. Ми офіційно встановимо пізніше, як це робиться. Спочатку розглянемо ще раз наш вступний невизначений інтеграл,$\int (20x+30)(x^2+3x-5)^9\ dx$. Мабуть, найбільш «складною» частиною цілісності є$(x^2+3x-5)^9$. Ми хочемо зробити це простіше; ми робимо це через заміну. Нехай$u=x^2+3x-5$. Таким чином

$$(x^2+3x-5)^9 = u^9.$$

Ми встановили$u$ як функцію$x$, тому тепер розглянемо диференціал$u$:

$$du = (2x+3)dx.$$

Майте на увазі,$dx$ що$(2x+3)$ і множаться;$dx$ це не «просто сидіти там».

Поверніться до початкового інтегралу і виконайте деякі підстановки через алгебру:

\[\begin{align} \int (20x+30)(x^2+3x-5)^9\ dx &= \int 10(2x+3)(x^2+3x-5)^9\ dx \\ &=\int 10(\underbrace{x^2+3x-5}_u)^9\underbrace{(2x+3)\ dx}_{du} \\ &=\int 10u^9\ du \\ &= u^{10} + C \quad \text{(replace $u$ with $x^2+3x-5$)}\\ &= (x^2+3x-5)^{10} +C\end{align}\]

Можна було б добре подивитися на це і подумати: «Я (начебто) стежив за тим, як це працювало, але я ніколи не міг придумати це самостійно», але процес можна дізнатися. Цей розділ містить численні приклади, завдяки яким читач отримає розуміння та математичну зрілість, що дозволить їм розглядати заміщення як природний інструмент при оцінці інтегралів.

Раніше ми заявляли, що інтеграція шляхом підміни «скасовує» правило ланцюга. Зокрема,$g(x)$ нехай$F(x)$ і диференційовані функції і розглянемо похідну від їх складу:

$$\frac{d}{dx}\Big(F\big(g(x)\big)\Big) = F'(g(x))g'(x).$$

Таким чином

$$\int F'(g(x))g'(x)\ dx = F(g(x)) + C.$$

Інтеграція шляхом підстановки працює шляхом розпізнавання функції «inside»$g(x)$ і заміни її змінною. Встановивши$u=g(x)$, ми можемо переписати похідну як

$$\frac{d}{dx}\Big(F\big(u\big)\Big) = F'(u)u'.$$

Так як$du = g'(x)dx$, ми можемо переписати вищезгаданий інтеграл як

$$\int F'(g(x))g'(x)\ dx = \int F'(u) du = F(u)+C = F(g(x))+ C.$$

Це поняття є важливим, тому ми повторюємо його в контексті теореми.

Теорема$\PageIndex{1}$: Integration by Substitution

$F$$g$Дозволяти і бути диференційованими функціями, де діапазон$g$ є інтервалом,$I$ що міститься в області$F$. Тоді

$$\int F'(g(x))g'(x)\ dx = F(g(x)) + C.$$

Якщо$u = g(x)$, то$du = g'(x)dx$ і

$$\int F'(g(x))g'(x)\ dx = \int F'(u)\ du = F(u)+C = F(g(x))+C.$$

Сенс підміни полягає в тому, щоб зробити крок інтеграції легким. Дійсно, крок$\int F'(u)\ du = F(u) + C$ виглядає легко, так як антипохідне від похідного$F$ є справедливим$F$, плюс константа. Задіяна «робота» - це правильна заміна. Не існує покрокового процесу, який можна запам'ятати; скоріше, досвід буде керівництвом. Щоб набратися досвіду, ми зараз приступимо до багатьох прикладів.

Приклад$\PageIndex{1}$: Integrating by substitution

Оцінити$\int x\sin(x^2+5)\ dx$.

Рішення

Знаючи, що заміна пов'язана з правилом ланцюга, ми вирішили дозволити$u$ бути «всередині» функції$\sin(x^2+5)$. (Це не завжди хороший вибір, але часто це найкраще місце для початку.)

Нехай$u = x^2+5$, отже$du = 2x\,dx$. Цілісний має$x\,dx$ термін, але не$2x\,dx$ термін. (Нагадаємо, що множення є комутативним, тому фізично$x$ не повинно бути поруч, щоб там був$x\,dx$ термін.)$dx$ Ми можемо розділити обидві сторони$du$ виразу на 2:

$$du = 2x\,dx \quad \Rightarrow \quad \frac12du = x\,dx.$$

Тепер ми можемо замінити.

$$\begin{align}\int x\sin(x^2+5)\ dx &= \int \sin(\underbrace{x^2+5}_u) \underbrace{x\ dx}_{\frac12du}\\ &= \int \frac12\sin u\ du\end{align}$$

\[\begin{align} \phantom{\int x\sin(x^2+5)\ dx} &= -\frac12\cos u + C \quad \text{ (now replace $u$ with $x^2+5$)}\\ &=-\frac12\cos(x^2+5) + C. \end{align}\]

Таким чином$\int x\sin(x^2+5)\ dx = -\frac12\cos(x^2+5)+C$. Ми можемо перевірити нашу роботу, оцінивши похідну правої сторони.

Приклад$\PageIndex{2}$: Integrating by substitution

Оцінити$\int \cos(5x)\ dx$.

Рішення

Знову давайте$u$ замінити функцію «всередині». Відпускаючи$u = 5x$, у нас є$du = 5dx$. Оскільки наш integrand не має$5dx$ члена, ми можемо розділити попереднє рівняння на,$5$ щоб отримати$\frac15du = dx$. Тепер ми можемо замінити.

$$\begin{align} \int \cos(5x)\ dx &= \int \cos(\underbrace{5x}_u) \underbrace{dx}_{\frac15du} \\&= \int \frac15\cos u \ du \\ &= \frac15\sin u + C \\&= \frac15\sin (5x)+C. \end{align}$$

Ми можемо знову перевірити свою роботу через диференціацію.

У попередньому прикладі виставлявся поширений, і простий, тип підміни. Функція «inside» була лінійною функцією (в даному випадку$y = 5x$). Коли внутрішня функція лінійна, результуюча інтеграція дуже передбачувана, викладена тут.

Ключова ідея 10: Заміна лінійною функцією

Розглянемо$\int F'(ax+b)\ dx$, де$a\neq 0$ і$b$ знаходяться константи. Пускання$u = ax+b$ дає$du = a\cdot dx$, приводячи до результату

$$\int F'(ax+b)\ dx = \frac{1}{a}F(ax+b) + C.$$

Таким чином$\int \sin (7x-4)\ dx = -\frac17\cos(7x-4)+C$. Наш наступний приклад може використовувати Key Idea 10, але ми будемо використовувати його лише після проходження всіх кроків.

Приклад$\PageIndex{3}$: Integrating by substituting a linear function

Оцінити$\int \frac{7}{-3x+1}\ dx$.

Рішення

Подивитися цей склад функцій$f(g(x))$, де$f(x) = 7/x$ і$g(x) = -3x+1$. Використовуючи наше розуміння підміни, ми дозволяємо$u = -3x+1$, внутрішня функція. Таким чином$du = -3dx$. Integrand не вистачає а$-3$; отже, розділіть попереднє рівняння$-3$ на отримання$-du/3 = dx$. Тепер ми можемо оцінити інтеграл через підстановку.

$$\begin{align} \int \frac{7}{-3x+1}\ dx &= \int \frac{7}{u}\frac{du}{-3} \\ &= \frac{-7}3\int \frac{du}{u} \\ &= \frac{-7}3\ln |u| + C\\ &=-\frac73\ln|-3x+1| + C. \end{align}$$

Використання Key Idea 10 швидше, визнаючи, що$u$ є лінійним і$a = -3$. Можна продовжувати писати всі кроки, поки вони не будуть зручні з цим конкретним ярликом.

Не всі інтеграли, які виграють від заміщення, мають чітку функцію «всередині». Кілька наведених нижче прикладів продемонструють способи, за допомогою яких це відбувається.

Приклад$\PageIndex{4}$: Integrating by substitution

Оцінити$\int \sin x\cos x\ dx$.

Рішення

Тут немає складу функції, щоб експлуатувати; скоріше, просто добуток функцій. Не бійтеся експериментувати; коли дається інтеграл для оцінки, часто корисно думати: «Якщо я дозволю$u$ бути цим, то$du$ повинно бути, що...» і подивитися, якщо це допомагає спростити інтеграл взагалі.

У цьому прикладі давайте встановимо$u = \sin x$. Тоді$du = \cos x\ dx$, який у нас є як частина integrand! Заміна стає дуже простою:

$$\begin{align} \int \sin x\cos x\ dx &= \int u\ du \\ &= \frac12u^2+ C \\ &= \frac12\sin^2 x + C. \end{align}$$

Добре б запитати: «Що буде, якщо ми дозволимо$u = \cos x$?» Результат так само легко знайти, але виглядає зовсім інакше. Завдання для читача полягає в тому, щоб оцінити інтегральне дозволяючи$u = \cos x$ і з'ясувати, чому відповідь однакова, але виглядає по-іншому.

Наші приклади поки що вимагали «базової заміни». Наступний приклад демонструє, як можна зробити заміни, які часто вражають нового учня як «нестандартного».

Приклад$\PageIndex{5}$: Integrating by substitution

Оцінити$\int x\sqrt{x+3}\ dx$.

Рішення

Розпізнавання складу функцій, безлічі$u = x+3$. Потім$du = dx$, даючи те, що здається спочатку простою заміною. Але на цьому етапі ми маємо:

$$\int x\sqrt{x+3}\ dx = \int x\sqrt{u}\ du.$$

Ми не можемо оцінити інтеграл, який має як a, так$x$ і$u$ a в ньому. Нам потрібно перетворити на$x$ вираз за участю просто$u$.

Оскільки ми встановили$u = x+3$, ми також можемо стверджувати, що$u-3 = x$. Таким чином, ми можемо замінити$x$ в integrand с$u-3$. Також буде корисно переписати$\sqrt{u}$ як$u^\frac12$.

$$\begin{align} \int x\sqrt{x+3} \ dx &= \int (u-3)u^\frac12\ du \\ &= \int \big(u^\frac32 - 3u^\frac12\big) \ du \\ &= \frac25u^\frac52 - 2u^\frac32 + C \\ &= \frac25(x+3)^\frac52 - 2(x+3)^\frac32 + C.\end{align}$$

Перевірка вашої роботи - це завжди гарна ідея. У цьому конкретному випадку буде потрібно деяка алгебра, щоб відповідь відповідала integrand у вихідній задачі.

Приклад$\PageIndex{6}$: Integrating by substitution

Оцінити$\int \frac{1}{x\ln x}\ dx$.

Рішення

Це ще один приклад, коли, здається, не існує очевидного складу функцій. Лінія мислення, що використовується в$\PageIndex{5}$ прикладі, корисна тут: виберіть щось для$u$ і подумайте, що це означає,$du$ повинно бути. Якщо$u$ можна вибрати таку, яка$du$ також з'являється в цілісності, то ми вибрали добре.

Вибір$u = 1/x$ робить$du = -1/x^2\ dx$; це не здається корисним. Однак установка$u = \ln x$ робить$du = 1/x\ dx$, яка є частиною цілісного. Таким чином:

$$\begin{align} \int \frac1{x\ln x}\ dx &= \int \frac{1}{\underbrace{\ln x}_{1/u}}\underbrace{\frac1x\ dx}_{du} \\ &= \int \frac1u\ du \\ &= \ln |u| + C \\ &= \ln | \ln x| + C.\end{align}$$

Остаточний відповідь цікавий; натуральне колода з натурального колоди. Візьміть похідну, щоб підтвердити, що ця відповідь дійсно правильна.

Інтеграли за участю тригонометричних функцій

Розділ 6.3 глибше заглиблюється в інтеграли різноманітних тригонометричних функцій; тут ми використовуємо підстановку, щоб встановити фундамент, на якому ми будемо спиратися.

Наступні три приклади допоможуть заповнити деякі відсутні шматочки нашого антидеривативного знання. Ми знаємо антипохідні синусоїдних і косинусних функцій; а як щодо інших стандартних функцій тангенс, котангенс, секанс і косеканс? Ми відкриваємо їх далі.

Приклад$\PageIndex{7}$: Integration by substitution: antiderivatives of $\tan x$

Оцінити$\int \tan x\ dx.$

Рішення

Попередній абзац встановив, що ми не знали антипохідних тангенса, отже, ми повинні припустити, що в цьому розділі ми дізналися щось, що може допомогти нам оцінити цей невизначений інтеграл.

Перепишіть$\tan x$ як$\sin x/\cos x$. Хоча наявність складу функцій може бути не відразу очевидним, визнайте, що$\cos x$ знаходиться «всередині»$1/x$ функції. Тому ми бачимо, чи$u = \cos x$ повертає установка придатні для використання результати. Отже$du = -\sin x\ dx$, ми маємо це$-du = \sin x\ dx$. Ми можемо інтегрувати:

$$\begin{align}\int \tan x \ dx &= \int \frac{\sin x}{\cos x}\ dx \\ &= \int \frac1{\underbrace{\cos x}_u}\underbrace{\sin x\ dx}_{-du} \\ &= \int \frac {-1}u \ du\\ &= -\ln |u| + C \\ &= -\ln |\cos x| + C.\end{align}$$

Деякі тексти воліють приводити$-1$ всередину логарифм у вигляді сили$\cos x$, як у:

$$\begin{align} -\ln |\cos x| + C &= \ln |(\cos x)^{-1}| + C\\ &= \ln \left| \frac{1}{\cos x}\right| + C\\&= \ln |\sec x| + C.\end{align}$$

Таким чином, результат, який вони дають, є$\int \tan x \ dx = \ln|\sec x| + C$. Ці дві відповіді рівнозначні.

Приклад$\PageIndex{8}$: Integrating by substitution: antiderivatives of $\sec x$

Оцінити$\int \sec x\ dx$.

Рішення

У цьому прикладі використовується чудовий трюк: помножте integrand на «1», щоб ми побачили, як інтегруватися чіткіше. В даному випадку пишемо «1» як

$$1 = \frac{\sec x + \tan x}{\sec x + \tan x}.$$

Це може здатися, що він вийшов з лівого поля, але це чудово працює. Розглянемо:

$$\begin{align} \int \sec x\ dx &= \int \sec x\cdot \frac{\sec x + \tan x}{\sec x + \tan x}\ dx \\ &= \int \frac{\sec^2 x + \sec x\tan x}{\sec x + \tan x}\ dx.\end{align}$$

Тепер нехай$u = \sec x+\tan x$; це означає$du = (\sec x\tan x+ \sec^2 x)\ dx$, що наш чисельник. Таким чином:

$$\begin{align} &= \int \frac{du}{u} \\ &= \ln |u| + C \\ &= \ln |\sec x+\tan x| + C.\end{align}$$

Ми можемо використовувати подібні методи до тих, що використовуються в Прикладах,$\PageIndex{6}$ і$\PageIndex{7}$ знайти антипохідні$\cot x$ і$\csc x$ (які читач може дослідити у вправах.) Підсумовуємо наші результати тут.

Теорема$\PageIndex{1}$: Antiderivatives of Trigonometric Functions

1. $\int \sin x \ dx = -\cos x +C$
2. $\int \cos x\ dx = \sin x + C$
3. $\int \tan x\ dx = -\ln|\cos x|+C$
4. $\int \csc x \ dx = -\ln|\csc x+\cot x| +C$
5. $\int \sec x\ dx = \ln|\sec x+\tan x| + C$
6. $\int \cot x\ dx = \ln|\sin x|+C$

Досліджуємо ще один поширений тригонометричний інтеграл.

Приклад$\PageIndex{9}$: Integration by substitution: powers of $\cos x$ and $\sin x$

Оцінити$\int \cos^2x\ dx$.

Рішення

У нас є склад функцій як$\cos^2x = \big(\cos x\big)^2$.

Однак установка$u = \cos x$ означає$du = -\sin x\ dx$, що у нас немає в інтегралі. Потрібна ще одна методика.

Процес, який ми будемо використовувати, полягає у використанні формули зменшення потужності для$\cos^2x$ (можливо, зверніться до задньої частини цього тексту для цієї формули), яка стверджує

$$\cos ^2x = \frac{1+\cos(2x)}{2}.$$

Праву частину цього рівняння інтегрувати не складно. У нас є:

$$\begin{align} \int \cos^2x\ dx &= \int \frac{1+\cos(2x)}2\ dx \\ &= \int \left( \frac12 + \frac12\cos(2x)\right)\ dx. \end{align}$$

Тепер використовуйте Key Idea 10:

$$\begin{align} &= \frac12x + \frac12\frac{\sin(2x)}{2} + C\\&= \frac12x + \frac{\sin(2x)}4 + C.\end{align}$$

Ми будемо значним чином використовувати цю техніку зниження потужності в майбутніх розділах.

Спрощення Integrand

Як правило, неохоче маніпулювати цілісним інтегралом; по-перше, наше розуміння інтеграції є слабким, і можна подумати, що робота з integrand неправильно змінить результати. Інтеграція шляхом заміщення працює з використанням іншої логіки: поки зберігається рівність, цілісним можна маніпулювати, щоб його формою було легше мати справу. Наступні два приклади демонструють поширені способи, за допомогою яких використання алгебри спочатку полегшує інтеграцію.

Приклад$\PageIndex{10}$: Integration by substitution: simplifying first

Оцінити$\displaystyle \int \frac{x^3+4x^2+8x+5}{x^2+2x+1}\ dx$.

Рішення

Можна спробувати почати з встановлення$u$ рівних чисельнику або знаменнику; у кожному випадку результат не є працездатним.

При роботі з раціональними функціями (тобто частками, що складаються з поліноміальних функцій), це майже універсальне правило, що все працює краще, коли ступінь чисельника менше ступеня знаменника. Звідси ми використовуємо поліноміальне ділення.

Пропускаємо специфіку кроків, але зауважимо,$x^2+2x+1$ що коли ділиться на$x^3+4x^2+8x+5$, вона йде в$x+2$ рази з залишком$3x+3$. Таким чином

$$\frac{x^3+4x^2+8x+5}{x^2+2x+1} = x+2 + \frac{3x+3}{x^2+2x+1}.$$

$x+2$Інтеграція проста. Фракцію можна інтегрувати$u = x^2+2x+1$, встановивши, даючи$du = (2x+2)\ dx$. Це дуже схоже на чисельник. Зверніть увагу, що$du/2 = (x+1)\ dx$ а потім врахуйте наступне:

$$\begin{align}\int \frac{x^3+4x^2+8x+5}{x^2+2x+1}\ dx & = \int \left(x+2 + \frac{3x+3}{x^2+2x+1}\right)\ dx \\ &= \int (x+2)\ dx + \int \frac{3(x+1)}{x^2+2x+1}\ dx \\ & = \frac12x^2+2x+C_1 + \int \frac{3}{u}\frac{du}{2} \\ &= \frac12x^2+2x+C_1 + \frac32\ln|u| + C_2 \\&= \frac12x^2+2x+\frac32\ln|x^2+2x+1| + C.\end{align}$$

У чомусь нам «пощастило» в тому, що після поділу підміну вдалося зробити. У наступних розділах ми розробимо методи обробки раціональних функцій, де заміна безпосередньо нездійсненна.

Приклад$\PageIndex{11}$: Integration by alternate methods

Оцінюйте$\displaystyle \int \frac{x^2+2x+3}{\sqrt{x}}\ dx$ як з підміною, так і без неї.

Рішення

Ми вже знаємо, як інтегрувати цей конкретний приклад. Перепишіть$\sqrt{x}$ як$x^\frac12$ і спростіть дріб:

$$\frac{x^2+2x+3}{x^{1/2}} = x^\frac32 + 2x^\frac12 + 3x^{-\frac12}.$$

Тепер ми можемо інтегруватися за допомогою правила харчування:

$$\begin{align} \int \frac{x^2+2x+3}{x^{1/2}}\ dx &= \int\left(x^\frac32 + 2x^\frac12 + 3x^{-\frac12}\right)\ dx\\ &= \frac25x^\frac52 + \frac43x^\frac32 + 6x^\frac12 + C\end{align}$$

Це абсолютно прекрасний підхід. Ми демонструємо, як це також можна вирішити за допомогою підміни, оскільки її реалізація досить розумна.

Нехай$u = \sqrt{x} = x^\frac12$; тому

\ [du =\ frac12x^ {-\ frac12} dx =\ frac {1} {2\ sqrt {x}}\ dx\ quad\ quad\ quad 2du =\ frac {1} {\ sqrt {x}}\ dx. $$

Це дає нам$\displaystyle \int \frac{x^2+2x+3}{\sqrt{x}}\ dx = \int (x^2+2x+3)\cdot2\ du$. Що нам робити з іншими$x$ термінами? Так як$u = x^\frac12$,$u^2 = x$, і т.д. потім ми можемо замінити$x^2$ і$x$ з відповідними повноваженнями$u$. Таким чином, ми маємо

$$\begin{align*}\int \frac{x^2+2x+3}{\sqrt{x}}\ dx &= \int (x^2+2x+3)\cdot2\ du\\ &= \int 2(u^4 + 2u^2 + 3)\ du \\ &= \frac25u^5 + \frac43u^3 + 6u + C \\&= \frac25x^\frac52 + \frac43x^\frac32 + 6x^\frac12+C,\end{align*}$$

що, очевидно, та сама відповідь, яку ми отримали раніше. У цій ситуації заміна, можливо, більше роботи, ніж наш інший метод. Фантастична річ у тому, що вона працює. Це демонструє, наскільки гнучка інтеграція.

Заміна та обернені тригонометричні функції

При вивченні похідних обернених функцій ми дізналися, що

$$\frac{d}{dx}\big(\tan^{-1}x\big) = \frac{1}{1+x^2}.$$

Застосовувати правило ланцюга до цього не складно; наприклад,

$$\frac{d}{dx}\big(\tan^{-1}5x\big) = \frac{5}{1+25x^2}.$$

Тепер ми досліджуємо, як підстановка може бути використана для «скасування» певних похідних, які є результатом правила ланцюга, застосованого до зворотних тригонометричних функцій. Почнемо з прикладу.

Приклад$\PageIndex{12}$: Integrating by substitution: inverse trigonometric functions

Оцінити$\int \frac{1}{25+x^2}\ dx$.

Рішення

Цілісний вигляд схожий на похідну від арктангенсної функції. Примітка:

\ [\ почати {вирівнювання}\ розрив {1} {25+x^2} &=\ гідророзриву {1} {25 (1+\ гідророзриву {x^2} {25})}\\ &=\ гідророзриву {1} {25 (1+\ ліворуч (\ frac {x} {5}\ праворуч) ^2)}\\
&=\ гідророзриву {1} {25}\ гідророзрив {1} {1+\ ліворуч (\ frac {x} {5}\ праворуч) ^2}\. \ end {вирівняти}\]

Таким чином

$$\int\frac{1}{25+x^2}\ dx = \frac{1}{25}\int \frac{1}{1+\left(\frac{x}{5}\right)^2}\ dx.$$

Це можна інтегрувати за допомогою підстановки. Набір$u = x/5$, отже,$du = dx/5$ або$dx=5du$. Таким чином

$$\begin{align}\int\frac{1}{25+x^2}\ dx &= \frac{1}{25}\int \frac{1}{1+\left(\frac{x}{5}\right)^2}\ dx \\ &= \frac15\int \frac{1}{1+u^2}\ du \\ &= \frac15\tan^{-1}u + C \\ &= \frac15\tan^{-1}\left(\frac x5\right)+C\end{align}$$

Приклад$\PageIndex{12}$ демонструє загальну техніку, яка може бути застосована до інших інтегралів, які призводять до зворотних тригонометричних функцій. Результати підсумовуються тут.

Теорема$\PageIndex{2}$: Integrals Involving Inverse Trigonomentric Functions

Нехай$a>0$.

1. $\displaystyle \int \frac{1}{a^2+x^2}\ dx = \frac1a\tan^{-1}\left(\frac{x}{a}\right) + C$
2. $\displaystyle \int \frac{1}{\sqrt{a^2-x^2}}\ dx = \sin^{-1}\left(\frac{x}{a}\right)+C$
3. $\displaystyle \int \frac{1}{x\sqrt{x^2-a^2}}\ dx = \frac1a\sec^{-1}\left(\frac{|x|}{a}\right)+C$

Давайте попрактикуємося, використовуючи теорему$\PageIndex{2}$.

Приклад$\PageIndex{13}$: Integrating by substitution: inverse trigonometric functions

Оцініть задані невизначені інтеграли.
$\ стиль відображення\ int\ frac {1} {9+x^2}\ dx,\ quad\ int\ frac {1} {x\ sqrt {x^2-\ frac {1} {100}}}\ dx\ квад\ int\ frac {1} {\ sqrt {5-x^2}}\ dx.\]

Рішення

На кожен можна відповісти за допомогою простого застосування теореми$\PageIndex{2}$.

$\displaystyle \int \frac{1}{9+x^2}\ dx = \frac13\tan^{-1} \frac x3 + C$, як$a = 3$.

$\displaystyle \int \frac{1}{x\sqrt{x^2-\frac{1}{100}}}\ dx = 10\sec^{-1}10x + C$, як$a = \frac1{10}$.

$\displaystyle \int \frac{1}{\sqrt{5-x^2}} = \sin^{-1}\frac{x}{\sqrt{5}}+C$, як$a = \sqrt{5}$.

Більшість застосувань$\PageIndex{2}$ теореми не такі прості. Наступні приклади показують деякі загальні інтеграли, до яких ще можна підійти за допомогою цієї теореми.

Приклад$\PageIndex{14}$: Integrating by substitution: completing the square

Оцінити$\displaystyle \int\frac{1}{x^2-4x+13}\ dx$.

Рішення

Спочатку цей інтеграл, здається, не має нічого спільного з інтегралами в теоремі$\PageIndex{2}$. Оскільки йому не вистачає квадратного кореня, він майже напевно не пов'язаний з дугоподібним або арксекантним. Це, однак, пов'язано з функцією арктангенса.

Ми бачимо це, заповнивши квадрат в знаменнику. Наведемо коротке нагадування про процес тут.

Почніть з квадратики з провідним коефіцієнтом 1. Вона буде мати вигляд$x^2 + bx + c$. Візьміть 1/2 з$b$, квадрат його і додати/відніміть його назад у вираз. Тобто,

$$\begin{align} x^2+bx+ c &= \underbrace{x^2 + bx + \frac{b^2}4}_{(x+b/2)^2} - \frac{b^2}4 + c\\&= \left(x+\frac b2\right)^2 + c-\frac{b^2}4\end{align}$$

У нашому прикладі беремо половину$-4$ і квадратично її, отримуючи$4$. Додаємо/віднімаємо його в знаменник наступним чином:

$$\begin{align}\frac{1}{x^2-4x+13} &= \frac{1}{\underbrace{x^2-4x+4}_{(x-2)^2}-4+13}\\ &=\frac{1}{(x-2)^2 + 9}\end{align}$$

Тепер ми можемо інтегрувати це за допомогою правила арктангенса. Технічно нам потрібно спочатку замінити$u=x-2$, але замість цього ми можемо використовувати Key Idea 10. Таким чином, ми маємо

$$\int \frac{1}{x^2-4x+13}\ dx = \int \frac{1}{(x-2)^2+9}\ dx = \frac13\tan^{-1}\frac{x-2}{3}+C.$$

Приклад$\PageIndex{15}$: Integrals requiring multiple methods

Оцінити$\displaystyle \int \frac{4-x}{\sqrt{16-x^2}}\ dx$.

Рішення

Цей інтеграл вимагає двох різних методів для його оцінки. Ми дістаємося до цих методів, розділивши інтеграл:

$$\int \frac{4-x}{\sqrt{16-x^2}}\ dx = \int \frac{4}{\sqrt{16-x^2}}\ dx - \int \frac{x}{\sqrt{16-x^2}}\ dx.$$

Перший інтеграл обробляється за допомогою простого застосування Теореми$\PageIndex{2}$; другий інтеграл обробляється заміщенням, з$u = 16-x^2$. Звертаємося з кожним окремо.

$\displaystyle \int \frac{4}{\sqrt{16-x^2}}\ dx = 4\sin^{-1}\frac{x}{4} + C.$

$\displaystyle \int\frac{x}{\sqrt{16-x^2}}\ dx$: Встановити$u = 16-x^2$, так$du = -2xdx$ і$xdx = -du/2$. У нас є

$$\begin{align} \int\frac{x}{\sqrt{16-x^2}}\ dx &= \int\frac{-du/2}{\sqrt{u}}\\ &= -\frac12\int \frac{1}{\sqrt{u}}\ du \\ &= - \sqrt{u} + C\\ &= -\sqrt{16-x^2} + C.\end{align}$$

Поєднуючи їх разом, ми маємо

$$\int \frac{4-x}{\sqrt{16-x^2}}\ dx = 4\sin^{-1}\frac x4 + \sqrt{16-x^2}+C.$$

Заміна та певна інтеграція

Цей розділ був зосереджений на оцінці невизначені інтеграли, оскільки ми вивчаємо нову техніку пошуку антипохідних. Однак значна частина часу інтеграція використовується в контексті певного інтеграла. Певні інтеграли, які потребують підстановки, можна обчислити за допомогою наступного робочого процесу:

1. Почніть з певного інтеграла$\displaystyle \int_a^b f(x)\ dx$, який вимагає підміни.
2. Ігнорувати межі; використовувати підстановку для оцінки$\displaystyle \int f(x)\ dx$ та пошуку антидериватива$F(x)$.
3. $F(x)$Оцінюйте за межами; тобто оцінюйте$F(x)\Big|_a^b = F(b) - F(a)$.

Цей робочий процес працює нормально, але заміна пропонує альтернативу, яка є потужною та дивовижною (і трохи економії часу).

За своєю суттю, (використовуючи позначення теореми$\PageIndex{1}$ заміщення) перетворює інтеграли виду$\displaystyle \int F'(g(x))g'(x)\ dx$ в інтеграл виду$\displaystyle \int F'(u)\ du$ з підміною$u = g(x)$. Наступна теорема стверджує, як можна змінювати межі певного інтеграла в міру виконання підстановки.

Теорема$\PageIndex{3}$: Substitution with Definite Integrals

$F$$g$Дозволяти і бути диференційованими функціями, де діапазон$g$ є інтервалом$I$, який міститься в області$F$. Тоді

$$\int_a^b F'\big(g(x)\big)g'(x)\ dx = \int_{g(a)}^{g(b)} F'(u)\ du.$$

Фактично, Теорема$\PageIndex{3}$ стверджує, що після перетворення на інтеграцію щодо$u$, вам не потрібно повертатися до оцінки щодо$x$. Кілька прикладів допоможуть розібратися.

Приклад$\PageIndex{16}$: Definite integrals and substitution: changing the bounds

Оцініть$\displaystyle \int_0^2 \cos(3x-1)\ dx$ за допомогою теореми$\PageIndex{3}$.

Рішення

Спостерігаючи за складом функцій$u=3x-1$, нехай, отже$du = 3dx. As \(3dx$\) не з'являється в цілісному вигляді, розділіть останнє рівняння на 3, щоб отримати$du/3 = dx$.

Встановлюючи$u = 3x-1$, ми неявно заявляємо, що$g(x) = 3x-1$. Теорема$\PageIndex{3}$ стверджує, що нова нижня межа є$g(0) = -1$; нова верхня межа є$g(2) = 5$. Тепер оцінюємо певний інтеграл:

$$\begin{align}\int_1^2 \cos(3x-1) \ dx &= \int_{-1}^5 \cos u \frac{du}{3} \\ &= \frac{1}{3} \sin u\Big|_{-1}^5 \\ &= \frac{1}{3}\big(\sin 5- \sin (-1)\big)\approx -0.039.\end{align}$$

Зверніть увагу, як тільки ми перетворили інтеграл бути з точки зору$u$, ми ніколи не поверталися до використання$x$.

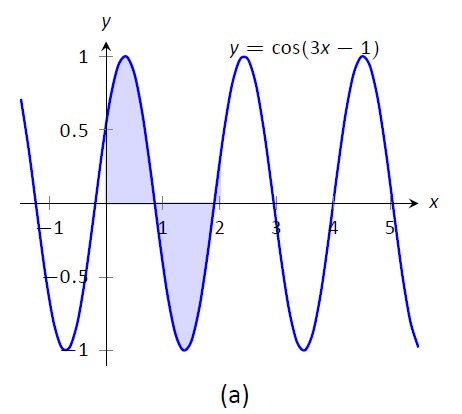
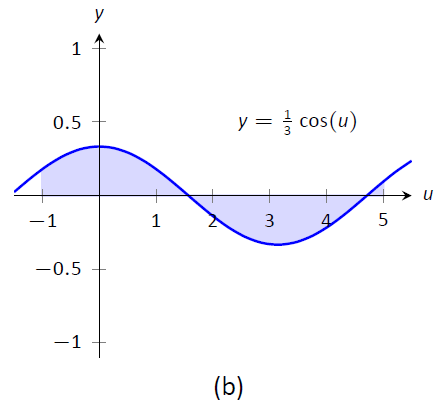
Малюнок$\PageIndex{1}$: Графік областей, визначених визначеними інтегралами Прикладу$\PageIndex{16}$

Графіки на малюнку$\PageIndex{1}$ розповідають більше про історію. У (a) область, визначена початковим інтегралом, затінюється, тоді як у (b) область, визначена новим інтегралом, затінюється. У цій конкретній ситуації райони виглядають дуже схожими; новий регіон «коротший», але «ширший», що дає таку ж площу.

Приклад$\PageIndex{17}$: Definite integrals and substitution: changing the bounds

Оцініть$\displaystyle \int_0^{\pi/2} \sin x \cos x\ dx$ за допомогою теореми$\PageIndex{3}$.

Рішення

Ми побачили відповідний невизначений інтеграл у прикладі$\PageIndex{4}$. У цьому прикладі ми встановили,$u = \sin x$ але заявили, що ми могли б дозволити$u = \cos x$. Для різноманітності ми робимо останнє тут.

Нехай$u = g(x) = \cos x$, даючи$du = -\sin x\ dx$ і значить$\sin x\ dx = -du$. Нова верхня межа є$g(\pi/2) = 0$; нова нижня межа є$g(0) = 1$. Зверніть увагу, як нижня межа насправді більша за верхню межу зараз. У нас є

$$\begin{align} \int_0^{\pi/2} \sin x\cos x\ dx &= \int_1^0 -u\ du \quad \text{\scriptsize (switch bounds \& change sign)}\\ &= \int_0^1 u\ du\\ &= \frac12u^2\Big|_0^1= 1/2.\\ \end{align}$$

На малюнку$\PageIndex{2}$ ми знову намалювали дві області, визначені нашими певними інтегралами. На відміну від попереднього прикладу, вони не несуть ніякої схожості один з одним. Однак теорема$\PageIndex{3}$ гарантує, що вони мають однакову площу.

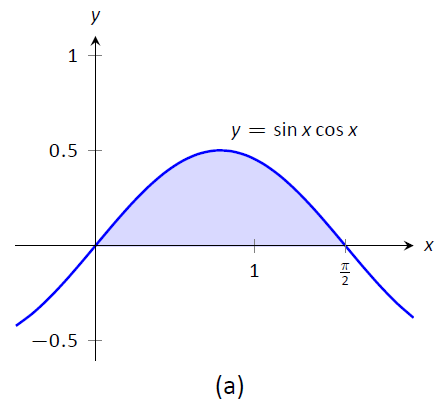
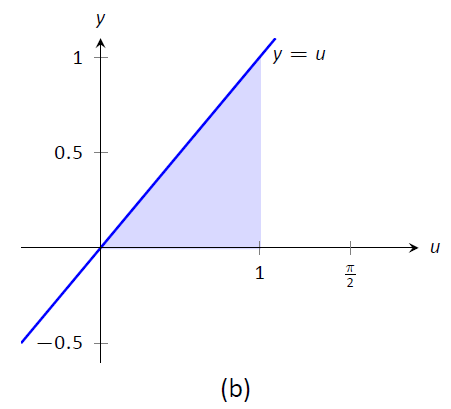
Малюнок$\PageIndex{2}$: Графік областей, визначених визначеними інтегралами Прикладу$\PageIndex{17}$.

Інтеграція шляхом заміщення є потужним і корисним методом інтеграції. Наступний розділ представляє ще одну техніку, яка називається Інтеграція частинами. Оскільки заміна «скасовує» правило ланцюга, інтеграція частинами «скасовує» Правило продукту. Разом ці дві методи забезпечують міцну основу, на якій базується більшість інших методів інтеграції.

Дописувачі та атрибуція

• Template:ContribApexCalc
• Template:ContribMarshall