6.3: Тригонометричні інтеграли

Last updated
Save as PDF

Page ID: 60814

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Функції, що включають тригонометричні функції, корисні, оскільки вони добре описують періодичну поведінку. У цьому розділі описано кілька методик знаходження антипохідних певних комбінацій тригонометричних функцій.

Інтеграли виду$\int \sin^m x\cos^n x\ dx$

Вивчаючи техніку підстановки, ми побачили інтеграл$\int \sin x\cos x\ dx$ в прикладі 6.1.4. Інтеграція не була складною, і можна було легко оцінити невизначений інтеграл, дозволяючи$u=\sin x$ або дозволяючи$u = \cos x$. Цей інтеграл простий, оскільки потужність як синуса, так і косинуса дорівнює 1.

Узагальнено цей інтеграл і розглянуто інтеграли виду$\int \sin^mx\cos^nx\ dx$, де$m,n$ невід'ємні цілі числа. Наша стратегія оцінки цих інтегралів полягає у використанні ідентичності$\cos^2x+\sin^2x=1$ для перетворення високих ступенів однієї тригонометричної функції в іншу, залишаючи один синус або косинус член в цілісному. Ми узагальнюємо загальну техніку в наступній Key Idea.

Ключова ідея 11: Інтеграли, що включають сили синуса та косинуса

Розглянемо$ \int \sin^mx\cos^nx\ dx$, де$m,n$ знаходяться невід'ємні цілі числа.

Якщо$m$ непарне, то$m=2k+1$ для деякого цілого числа$k$. Переписати $\ sin^mx =\ sin^ {2k+1} х =\ sin^ {2k} х\ sin x = (\ sin^2x) ^k\ sin x = (1-\ cos^2x) ^k\ sin x.$$ Тоді $\ int\ sin^mx\ cos^nx =\ int (1-\ cos^2x) ^k\ sin x\ cos^nx\ dx = -\ int (1-u^2) ^ku^n\ du, $ де$u = \cos x$ і$du = -\sin x\ dx$.
Якщо$n$ непарно, то використовуючи заміни, подібні до описаних вище, ми маємо $$\ int\ sin^mx\ cos^nx\ dx =\ int u^m (1-u^2) ^k\ du, $$ де$u = \sin x$ і$du = \cos x\ dx$.
Якщо обидва$m$ і$n$ парні, використовуйте тотожності зменшення потужності $$\ cos^2x =\ frac {1+\ cos (2x)} {2}\ quad\ text {і}\ quad\ sin^2x =\ frac {1-\ cos (2x)} 2$$ для зменшення ступеня інтеграції. Розгорніть результат і знову застосуйте принципи цієї ключової ідеї.

Ми практикуємо застосування Key Idea 11 в наступних прикладах.

Приклад$\PageIndex{1}$: Integrating powers of sine and cosine

Оцініть$\int\sin^5x\cos^8x\ dx$.

Рішення

Потужність синусоїда непарна, тому ми переписуємо$\sin^5x$ як

\[\sin^5x = \sin^4x\sin x = (\sin^2x)^2\sin x = (1-\cos^2x)^2\sin x. \nonumber \]

Наш невід'ємний зараз$ \int (1-\cos^2x)^2\cos^8x\sin x\ dx$. Нехай$u = \cos x$, отже$du = -\sin x\ dx$. Здійснення заміщення та розширення цілісності дає

\[\int (1-\cos^2)^2\cos^8x\sin x\ dx = -\int (1-u^2)^2u^8\ du = -\int \big(1-2u^2+u^4\big)u^8\ du = -\int \big(u^8-2u^{10}+u^{12}\big)\ du. \nonumber \]

Цей кінцевий інтеграл не складно оцінити, даючи

\[\begin{align*} -\int \big(u^8-2u^{10}+u^{12}\big)\ du &= -\frac19u^9 + \frac2{11}u^{11} - \frac1{13}u^{13} + C \\[4pt] &=-\frac19\cos^9 x + \frac2{11}\cos^{11} x - \frac1{13}\cos^{13} x + C.\end{align*}\]

Приклад$\PageIndex{2}$: Integrating powers of sine and cosine

Оцініть$\int\sin^5x\cos^9x\ dx$.

Рішення

Потужності як синусоїдів, так і косинусів непарні, тому ми можемо застосувати методи Key Idea 11 до будь-якої потужності. Ми вирішили працювати з силою терміна косинуса, оскільки в попередньому прикладі використовувалася сила синусоїда.

Переписуємо$\cos^9x$ як

\[\begin{align*} \cos^9 x &= \cos^8x\cos x \\[4pt] &= (\cos^2x)^4\cos x \\[4pt] &= (1-\sin^2x)^4\cos x \\[4pt] &= (1-4\sin^2x+6\sin^4x-4\sin^6x+\sin^8x)\cos x.\end{align*}\]

Переписуємо інтеграл як

\[\int\sin^5x\cos^9x\ dx = \int\sin^5x\big(1-4\sin^2x+6\sin^4x-4\sin^6x+\sin^8x\big)\cos x\ dx. \nonumber \]

Тепер підставляємо і інтегруємо, використовуючи$u = \sin x $ і$du = \cos x\ dx$.

\[\begin{align*} \int u^5(1-4u^2+6u^4-4u^6+u^8)\ du &= \int\big(u^5-4u^7+6u^9-4u^{11}+u^{13}\big)\ du \\[4pt]&= \frac16u^6-\frac12u^8+\frac35u^{10}-\frac13u^{12}+\frac{1}{14}u^{14}+C\\[4pt] &= \frac16\sin^6 x-\frac12\sin^8 x+\frac35\sin^{10} x+\ldots\\[4pt]&\phantom{=}-\frac13\sin^{12} x+\frac{1}{14}\sin^{14} x+C.\end{align*}\]

Примітка технології: Робота, яку ми тут виконуємо, може бути трохи стомлюючою, але важливі навички (вирішення проблем, алгебраїчні маніпуляції тощо). У наш час проблеми такого роду часто вирішуються за допомогою системи комп'ютерної алгебри. Потужна програма Mathematica інтегрується$\int \sin^5x\cos^9x\ dx$ як

\[f(x)=-\frac{45 \cos (2 x)}{16384}-\frac{5 \cos (4 x)}{8192}+\frac{19 \cos (6x)}{49152}+\frac{\cos (8x)}{4096}-\frac{\cos (10 x)}{81920}-\frac{\cos (12 x)}{24576}-\frac{\cos (14 x)}{114688},\]

який явно має іншу форму, ніж наша відповідь у$\PageIndex{2}$ прикладі, який

\[g(x)=\frac16\sin^6 x-\frac12\sin^8 x+\frac35\sin^{10} x-\frac13\sin^{12} x+\frac{1}{14}\sin^{14} x.\]

На малюнку$\PageIndex{1}$ зображений графік$f$ і$g$; вони явно не рівні, але відрізняються лише константою. Тобто$g(x) = f(x) + C$ для якоїсь постійної$C$. Таким чином, у нас є два різних антипохідних однієї функції, тобто обидві відповіді є правильними.

$альт$

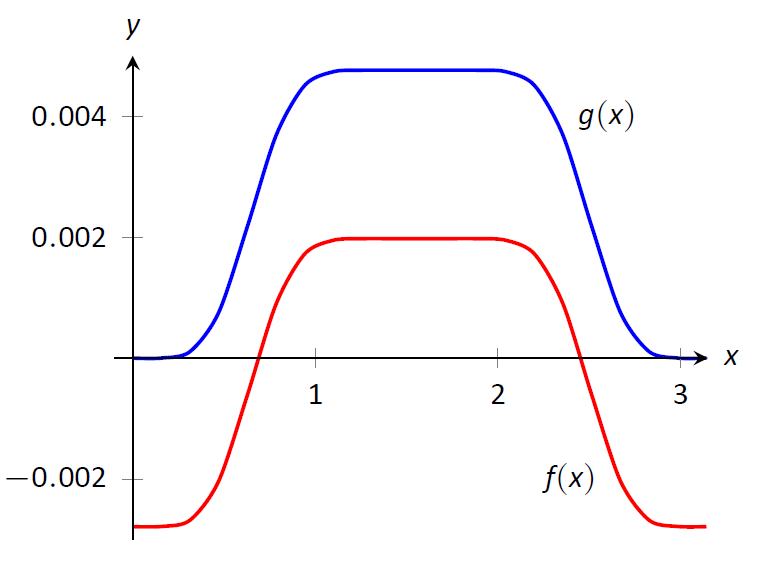
Малюнок$\PageIndex{1}$: Сюжет$f(x)$ і$g(x)$ з Прикладу$\PageIndex{2}$ та Технологічної Примітки.

Приклад$\PageIndex{3}$: Integrating powers of sine and cosine

Оцініть$\int\cos^4x\sin^2x\ dx$.

Рішення

Синус і косинус однакові, тому ми використовуємо формули зменшення потужності і алгебру наступним чином.

\[\begin{align*}\int \cos^4x\sin^2x\ dx &= \int\left(\frac{1+\cos(2x)}{2}\right)^2\left(\frac{1-\cos(2x)}2\right)\ dx \\[4pt] &= \int\frac{1+2\cos(2x)+\cos^2(2x)}4\cdot\frac{1-\cos(2x)}2\ dx\\[4pt] &= \int \frac18\big(1+\cos(2x)-\cos^2(2x)-\cos^3(2x)\big)\ dx\end{align*}\]

$\cos(2x)$Термін легко інтегрується, особливо з Key Idea 10. $\cos^2(2x)$Термін - це ще один тригонометричний інтеграл з рівною потужністю, що вимагає формули зменшення потужності знову. $\cos^3(2x)$Термін - це косинусна функція з непарною потужністю, що вимагає заміни, як це робилося раніше. Ми інтегруємо кожен по черзі нижче.

\[\int\cos(2x)\ dx = \frac12\sin(2x)+C.\nonumber \]

\[\int\cos^2(2x)\ dx = \int \frac{1+\cos(4x)}2\ dx = \frac12\big(x+\frac14\sin(4x)\big)+C. \nonumber \]

Нарешті, переписуємо$\cos^3(2x)$ як

\[\cos^3(2x) = \cos^2(2x)\cos(2x) = \big(1-\sin^2(2x)\big)\cos(2x).\]

Відпускаючи$u=\sin(2x)$, у нас$du = 2\cos(2x)\ dx$, звідси

\[\begin{align*} \int \cos^3(2x)\ dx &= \int\big(1-\sin^2(2x)\big)\cos(2x)\ dx\\[4pt] &= \int \frac12(1-u^2)\ du\\[4pt] &= \frac12\Big(u-\frac13u^3\Big)+C\\[4pt] &= \frac12\Big(\sin(2x)-\frac13\sin^3(2x)\Big)+C\end{align*}\]

Збираючи всі шматки воєдино, у нас є

\[\begin{align*}\int \cos^4x\sin^2x\ dx &=\int \frac18\big(1+\cos(2x)-\cos^2(2x)-\cos^3(2x)\big)\ dx \\[4pt] &= \frac18\Big[x+\frac12\sin(2x)-\frac12\big(x+\frac14\sin(4x)\big)-\frac12\Big(\sin(2x)-\frac13\sin^3(2x)\Big)\Big]+C \\[4pt] &=\frac18\Big[\frac12x-\frac18\sin(4x)+\frac16\sin^3(2x)\Big]+C\end{align*}\]

Процес вище був трохи довгим і нудним, але можливість працювати з такою проблемою, як це, від початку до кінця важливо.

Інтеграли виду$\int\sin(mx)\sin(nx)\ dx,$$\int \cos(mx)\cos(nx)\ dx$, і$\int \sin(mx)\cos(nx)\ dx$.

Функції, які містять продукти синусів і косинусів різних періодів, важливі в багатьох додатках, включаючи аналіз звукових хвиль. Інтеграли виду

\[\int\sin(mx)\sin(nx)\ dx,\quad \int \cos(mx)\cos(nx)\ dx \quad \text{and}\quad\int \sin(mx)\cos(nx)\ dx\]

найкраще підходити, застосувавши формули продукту до суми, знайдені на задній обкладинці цього тексту, а саме

\[\begin{align*} \sin(mx)\sin(nx) &= \frac12\Big[\cos\big((m-n)x\big)-\cos\big((m+n)x\big)\Big] \\[4pt]\cos(mx)\cos(nx) &= \frac12\Big[\cos\big((m-n)x\big)+\cos\big((m+n)x\big)\Big] \\[4pt]\sin(mx)\cos(nx) &= \frac12\Big[\sin\big((m-n)x\big)+\sin\big((m+n)x\big)\Big]\end{align*}\]

Приклад$\PageIndex{4}$: Integrating products of $\sin(mx)$ and $\cos(nx)$

Оцініть$\int\sin(5x)\cos(2x)\ dx$.

Рішення

Застосування формули та подальша інтеграція прості:

\[\begin{align*}\int\sin(5x)\cos(2x)\ dx &= \int \frac12\Big[\sin(3x)+\sin(7x)\Big]\ dx \\[4pt] &= -\frac16\cos(3x) - \frac1{14}\cos(7x) + C\end{align*}\]

Інтеграли виду$\int\tan^mx\sec^nx\ dx$.

При оцінці інтегралів виду$\int \sin^mx\cos^nx\ dx$ теорема Піфагора дозволила нам перетворювати парні сили синуса в парні сили косинуса, і навпаки. Якщо, наприклад, сила синуса була непарною, ми витягнули один$\sin x$ і перетворили решту парної потужності$\sin x$ в функцію, використовуючи повноваження$\cos x$, що призводить до легкої заміни.

Та ж базова стратегія відноситься і до інтегралів форми$\int \tan^mx\sec^n x\ dx$, хоча і трохи більш нюансованих. Наступні три факти виявляться корисними:

$\frac{d}{dx}(\tan x) = \sec^2x$,
$\frac{d}{dx}(\sec x) = \sec x\tan x$, і
$1+\tan^2x = \sec^2x$(Теорема Піфагора).

Якщо integrand можна маніпулювати, щоб розділити$\sec^2x$ термін з рештою секантної влади навіть, або якщо$\sec x\tan x$ термін може бути розділений з рештою$\tan x$ влади навіть, теорема Піфагора може бути використана, що призводить до простої підміни. Ця стратегія викладена в наступній Key Idea.

Ключова ідея 12: Інтеграли, що включають сили дотичної та секансної

Розглянемо$\int\tan^mx\sec^nx\ dx$, де$m,n$ знаходяться невід'ємні цілі числа.

Якщо$n$ парне, то$n=2k$ для деякого цілого числа$k$. Перепишіть$\sec^nx$ як $\ сек^nx =\ сек^ {2k} х =\ сек^ {2k-2} х\ сек^2x = (1+\ tan^2x) ^ {k-1}\ сек^2x.$$ Потім $\ int\ tan^mx\ sec^nx\ dx=\ int\ tan^mx (1+\ tan^2x) ^ {k-1} сек^2x\ dx =\ int u^m (1+u^2) ^ {k-1}\ du, $ де$u = \tan x$ і$du = \sec^2x\ dx$.
Якщо$m$ непарне, то$m=2k+1$ для деякого цілого числа$k$. Перепишіть$\tan^mx\sec^nx$ як $\ tan^mx\ сек ^ nx =\ tan^ {2k+1} х\ сек^nx =\ tan^ {2k} х\ сек^ {n-1} х\ сек х\ сек x\ tan x = (\ сек^2x-1) ^k\ sec^ {n-1} х\ сек х\ tan x.$$ Тоді $\ int\ tan ^ mx\ сек ^ x\ dx=\ int (\ сек^2x-1) ^k\ сек^ {n-1} х\ сек х\ тан х\ dx =\ int (u^2-1) ^ku^ {n-1}\ du, $ де$u = \sec x$ і$du = \sec x\tan x\ dx$.
Якщо$n$ непарне і$m$ парне, то$m=2k$ для деякого цілого числа$k$. Перетворити$\tan^mx $ на$(\sec^2x-1)^k$. Розгорніть новий integrand і використовуйте інтеграцію по частинам, з$dv = \sec^2x\ dx$.
Якщо$m$ парний і$n=0$, перепишіть$\tan^mx$ як $\ tan^mx =\ tan^ {м-2} х\ tan^2x =\ tan^ {м-2} х (\ сек ^ 2x-1) =\ tan^ {м-2}\ sec^2x-\ tan^ {м-2} x.$$ Так $$\ int\ tan^mx\ dx =\ underbrace {\ int\ tan^ {м-2} x.$ Так $\ int\ tan^mx\ dx =\ underbrace {\ int\ tan^ {м-2} x.$ Так $\ int\ tan 2}\ sec^2x\ dx} _ {\ text {\ мале застосувати правило\ #1}}\ quad -\ underbrace {\ int\ tan^ {м-2} x\ dx} _ {\ text {\ маленьке застосувати правило\ # 4 знову}} . $$

Методи, описані в пунктах 1 і 2 Key Idea 12, відносно прості, але прийоми в пунктах 3 і 4 можуть бути досить виснажливими. Кілька прикладів допоможуть з цими методами.

Приклад$\PageIndex{5}$: Integrating powers of tangent and secant

Оцініть$\int \tan^2x\sec^6x\ dx$.

Рішення

Оскільки сила секансу рівна, ми використовуємо правило #1 з Key Idea 12 і витягуємо a$\sec^2x$ в integrand. Решта степеней секансу перетворюємо в сили дотичної.

\[\begin{align*}\int \tan^2x\sec^6x\ dx &= \int\tan^2x\sec^4x\sec^2x\ dx \\[4pt] &= \int \tan^2x\big(1+\tan^2x\big)^2\sec^2x\ dx \end{align*}\]

Тепер підставляємо, з$u=\tan x$, с$du = \sec^2x\ dx$.

\[=\int u^2\big(1+u^2\big)^2\ du \nonumber \]

Ми залишаємо інтеграцію і подальшу підміну читачеві. Остаточна відповідь:

\[=\frac13\tan^3x+\frac25\tan^5x+\frac17\tan^7x+C. \nonumber \]

Приклад$\PageIndex{6}$: Integrating powers of tangent and secant

Оцініть$\int \sec^3x\ dx$.

Рішення

Ми застосовуємо правило #3 з Key Idea 12, оскільки сила секанса непарна, а сила тангенса парна (0 - парне число). Ми використовуємо інтеграцію частинами; правило пропонує дозволити$dv = \sec^2x\ dx$, це означає, що$u = \sec x$.

\[\begin{align*}u&= \sec x & v&=\text{?}\\[4pt]du&= \text{?} & dv&=\sec^2 x\ dx\end{align*}\]

Малюнок$\PageIndex{2}$: Налаштування інтеграції по частинам.

Використовуючи інтеграцію частинами, ми маємо

\[\begin{align*}\int \sec^3x\ dx &= \int \underbrace{\sec x}_u\cdot\underbrace{\sec^2 x\ dx}_{dv}\\[4pt] &= \sec x\tan x - \int \sec x\tan^2x\ dx. \end{align*}\]

Цей новий інтеграл також вимагає застосування правила\ #3 Key Idea:

\[\begin{align*} &= \sec x\tan x - \int \sec x \big(\sec^2 x-1\big)\ dx\\[4pt] &= \sec x\tan x - \int \sec^3x\ dx + \int \sec x\ dx \\[4pt] &= \sec x\tan x -\int \sec^3x\ dx + \ln|\sec x+\tan x| \\[4pt] \end{align*}\]

У попередніх програмах інтеграції частинами ми бачили, де оригінальний інтеграл знову з'явився в нашій роботі. Ми вирішуємо це шляхом додавання$\int \sec^3x\ dx$ до обох сторін, даючи:

\[\begin{align*} 2\int \sec^3x\ dx &= \sec x\tan x + \ln|\sec x+\tan x| \\[4pt]\int \sec^3x\ dx &= \frac12\Big(\sec x\tan x + \ln|\sec x+\tan x|\Big)+C\end{align*}\]

Наведемо ще один приклад.

Приклад$\PageIndex{7}$: Integrating powers of tangent and secant

Оцініть$\int\tan^6x\ dx$.

Рішення

Ми використовуємо правило #4 Ключової ідеї 12.

\[\begin{align*} \int \tan^6x\ dx &= \int \tan^4x\tan^2x\ dx \\[4pt] &= \int\tan^4x\big(\sec^2x-1\big)\ dx\\[4pt] &= \int\tan^4x\sec^2x\ dx - \int\tan^4x\ dx \end{align*}\]

Інтегруйте перший інтеграл із заміною$u=\tan x$; інтегруйте другий, використовуючи правило #4 знову.

\[\begin{align*} &= \frac15\tan^5x-\int\tan^2x\tan^2x\ dx\\[4pt] &= \frac15\tan^5x-\int\tan^2x\big(\sec^2x-1\big)\ dx \\[4pt]&= \frac15\tan^5x -\int\tan^2x\sec^2x\ dx + \int\tan^2x\ dx\\[4pt] \end{align*}\]

Знову ж таки, використовуйте підстановку для першого інтеграла і правило\ #4 для другого.

\[\begin{align*} &= \frac15\tan^5x-\frac13\tan^3x+\int\big(\sec^2x-1\big)\ dx \\[4pt] &= \frac15\tan^5x-\frac13\tan^3x+\tan x - x+C. \end{align*}\]

Ці останні приклади, безумовно, були довгими, з неодноразовим застосуванням одного і того ж правила. Намагайтеся не перевантажувати довжину проблеми, а краще захоплюйтеся тим, наскільки надійним є цей метод рішення. Тригонометрична функція великої потужності може систематично зводитися до тригонометричних функцій нижчих ступенів до тих пір, поки не будуть обчислені всі антипохідні.

У наступному розділі представлена методика інтеграції, відома як тригонометрична заміна, розумна комбінація заміщення та теорема Піфагора.