2.7: Похідні обернених функцій

Нагадаємо,$y=f(x)$ що функція, як кажуть, одна до одного, якщо вона проходить тест горизонтальної лінії; тобто для двох різних$x$ значень$x_1$ і$x_2$, у нас немає$f(x_1)=f(x_2)$. У деяких випадках домен$f$ повинен бути обмежений таким чином, щоб він був один до одного. Наприклад, розгляньте$f(x)=x^2$. $f(-1)= f(1)$Зрозуміло,$f$ що так не один до одного на своєму звичайному домені, але, обмежуючись$f$$(0,\infty)$,$f$ є один до одного.

Тепер нагадаємо, що один до одного функції мають зворотні. Тобто, якщо$f$ один до одного, він має обернену функцію, позначається тим$f^{-1}$, що якщо$f(a)=b$, то$f^{-1}(b) = a$. Домен$f^{-1}$ - це діапазон$f$, і навпаки. Для зручності позначення встановлюємо$g=f^{-1}$ і трактуємо$g$ як функцію$x$.

Так як$f(a)=b$ має на увазі$g(b)=a$, коли$g$ ми складаємо$f$ і отримуємо приємний результат: $$f\big(g(b)\big) = f(a) = b.$$ Загалом,$f\big(g(x)\big) =x$ і$g\big(f(x)\big) = x$. Це дає нам зручний спосіб перевірити, чи є дві функції зворотними один одному: скласти їх, а якщо результат є$x$, то вони є зворотними (на відповідних доменах.)

Коли точка$(a,b)$ лежить на графіку$f$, точка$(b,a)$ лежить на графіку$g$. Це змушує нас виявити, що графік$g$ - це відображення$f$ через лінію$y=x$. На малюнку 2.29 ми бачимо функцію з графіком разом з її зворотним. Подивіться, як точка$(1,1.5)$ лежить на одному графіку, тоді як$(1.5,1)$ лежить на іншому. Через ці відносини все, про що ми знаємо,$f$ можна швидко перенести в знання про$g$.

Малюнок 2.29: Функція$f$ разом з її оберненою$f^{-1}$. (Зверніть увагу, як це не має значення, яку функцію ми$f$ називаємо; інша є$f^{-1}$.)

Для прикладу розглянемо малюнок 2.30, де$(a,b)$ проводиться дотична лінія до$f$ точки. Ця лінія має нахил$f^\prime(a)$. Через відображення поперек$y=x$, ми бачимо, що дотична лінія до$g$ точки$(b,a)$ повинна мати нахил$\frac{1}{f^\prime(a)}$. Це говорить нам про те, що$g^\prime(b) = \frac{1}{f^\prime(a)}.$

Малюнок 2.30: Відповідні дотичні лінії, намальовані до$f\text{ and }f^{-1}$.

Розглянемо:

Ми виявили взаємозв'язок між$f^\prime$ і$g^\prime$ в основному графічним способом. Ми також можемо реалізувати цей зв'язок аналітично. Нехай$y = g(x)$, де знову$g = f^{-1}$. Ми хочемо знайти$y^\prime$. Так як$y = g(x)$, ми це знаємо$f(y) = x$. Використовуючи правило ланцюга та неявну диференціацію, візьміть похідну обох сторін цієї останньої рівності.

$$\begin{align*}\frac{d}{dx}\Big(f(y)\Big) &= \frac{d}{dx}\Big(x\Big) \\ f^\prime(y)\cdot y^\prime &= 1\\ y^\prime &= \frac{1}{f^\prime(y)}\\ y^\prime &= \frac{1}{f^\prime(g(x))} \end{align*}$$

Це призводить нас до наступної теореми.

Теорема 22: Похідні обернених функцій

$f$Дозволяти диференційовний і один до одного на відкритому інтервалі$I$$I$, де$f^\prime(x) \neq 0$ для всіх$x$ в,$J$$g$ Дозволяти бути діапазон$f$ на$I$, нехай бути зворотна функція$f$, і нехай$f(a) = b$ для деяких$a$ в$I$. Тоді$g$ є диференційована функція на$J$, і зокрема,

$1. \left(f^{-1}\right)^\prime (b)=g^\prime (b) = \frac{1}{f^\prime(a)}$\ квад\ текст {і}\ квад 2. \ ліворуч (f^ {-1}\ праворуч) ^\ правий (x) =g^\ правий (x) =\ frac {1} {f^\ прайм (g (x))}\)

Результати Теореми 22 не є тривіальними; позначення спочатку може здатися заплутаним. Уважний розгляд, поряд з прикладами, повинен заслужити розуміння.

У наступному прикладі ми застосуємо Теорему 22 до функції arcsine.

Приклад 75: Пошук похідної оберненої тригонометричної функції

Нехай$y = \arcsin x = \sin^{-1} x$. Знайти$y^\prime$ за допомогою теореми 22.

Малюнок 2.32: Прямокутний трикутник, який визначається$y=\sin^{-1}(x/1)$ довжиною третього катета, знайденого за допомогою теореми Піфагора.

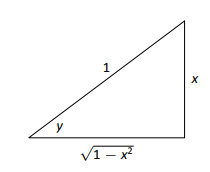
Рішення

Прийнявши наші раніше визначені позначення, нехай$g(x) = \arcsin x$ і$f(x) = \sin x$. Таким чином$f^\prime(x) = \cos x$. Застосовуючи теорему, ми маємо

$$\begin{align*} g^\prime (x) &= \frac{1}{f^\prime(g(x))} \\ &= \frac{1}{\cos(\arcsin x)}. \end{align*}$$

Це останній вислів не відразу висвітлює. Намалювати фігуру допоможе, як показано на малюнку 2.32. Нагадаємо, що синусоїдальну функцію можна розглядати як прийняття кута і повертає співвідношення сторін прямокутного трикутника, зокрема, відношення «протилежне над гіпотенузою». Це означає, що функція arcsine приймає як вхід співвідношення сторін і повертає кут. Рівняння$y=\arcsin x$ можна переписати як$y=\arcsin (x/1)$; тобто розглянути прямокутний трикутник, де гіпотенуза має довжину 1, а сторона, протилежна куту з мірою,$y$ має довжину$x$. Це означає, що кінцева сторона має довжину$\sqrt{1-x^2}$, використовуючи теорему Піфагора.

$$\text{Therefore }\cos (\sin^{-1} x) = \cos y = \sqrt{1-x^2}/1 = \sqrt{1-x^2},\text{ resulting in }$$ $$\frac{d}{dx}\big(\arcsin x\big) = g^\prime (x) = \frac{1}{\sqrt{1-x^2}}.$$

Пам'ятайте, що вхід$x$ функції арксина - це відношення сторони прямокутного трикутника до його гіпотенузи; абсолютне значення цього відношення ніколи не буде більше 1. Тому внутрішня частина квадратного кореня ніколи не буде негативною.

Для того, щоб зробити$y=\sin x$ один до одного, ми обмежуємо його домен до$[-\pi/2,\pi/2]$; на цьому домені діапазон є$[-1,1]$. Тому домен$y=\arcsin x$ є$[-1,1]$ і діапазон є$[-\pi/2,\pi/2]$. Коли$x=\pm 1$, зверніть увагу, як похідна від функції арксина невизначена; це відповідає тому, що як$x\to \pm1$, дотичні лінії до арксину наближаються до вертикальних ліній з невизначеними нахилами.

На малюнку 2.33 ми бачимо$f(x) = \sin x$ та$f^{-1} = \sin^{-1} x$ розміщуємо графіки на відповідних доменах. Лінія, дотична до$\sin x$ точки,$(\pi/3, \sqrt{3}/2)$ має нахил$\cos \pi/3 = 1/2$. Нахил відповідної точки на$\sin^{-1}x$, точці$(\sqrt{3}/2,\pi/3)$, ще раз $$\frac{1}{\sqrt{1-(\sqrt{3}/2)^2}} = \frac{1}{\sqrt{1-3/4}} = \frac{1}{\sqrt{1/4}} = \frac{1}{1/2}=2,$$ перевіряє, що у відповідних точках функція та її зворотний мають взаємні нахили.

Малюнок 2.33: Графіки$\sin x \text{ and }\sin^{-1} x$ поряд з відповідними дотичними лініями.

Використовуючи подібні методи, ми можемо знайти похідні всіх обернених тригонометричних функцій. На малюнку 2.31 ми показуємо обмеження доменів стандартних тригонометричних функцій, що дозволяють їх бути оборотними.

Малюнок 2.31: Домени і діапазони тригонометричних і обернених тригонометричних функцій.

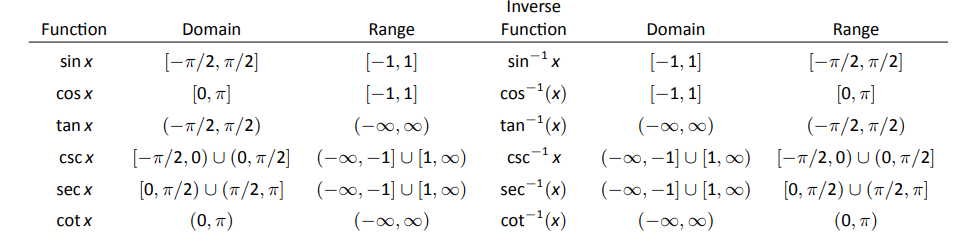
Теорема 23: Похідні обернених тригонометричних функцій

Обернені тригонометричні функції диференційовані на всіх відкритих множині, що містяться в їх областях (як зазначено на рис. 2.31), а їх похідні такі:

$$\begin{align} &1. \frac{d}{dx}\big(\sin^{-1}(x)\big) = \frac{1}{\sqrt{1-x^2}} \qquad &&4.\frac{d}{dx}\big(\cos^{-1}(x)\big) = -\frac{1}{\sqrt{1-x^2}} \\ &2.\frac{d}{dx}\big(\sec^{-1}(x)\big) = \frac{1}{|x|\sqrt{x^2-1}} &&5.\frac{d}{dx}\big(\csc^{-1}(x)\big) = -\frac{1}{|x|\sqrt{x^2-1}} \\ &3.\frac{d}{dx}\big(\tan^{-1}(x)\big) = \frac{1}{1+x^2} &&6.\frac{d}{dx}\big(\cot^{-1}(x)\big) = -\frac{1}{1+x^2} \end{align}$$

Зверніть увагу, як останні три похідні є лише протилежностями перших трьох відповідно. Через це перші три використовуються практично виключно у всьому цьому тексті.

У розділі 2.3 ми заявили, що без доказів чи пояснень$\frac{d}{dx}\big(\ln x\big) = \frac{1}{x}$. Ми можемо обґрунтувати, що зараз використовуємо теорему 22, як показано на прикладі.

Приклад 76: Пошук похідної від y = ln x

Використовуйте теорему 22 для обчислення$\frac{d}{dx}\big(\ln x\big)$.

Рішення

Подивитися$y= \ln x$ як зворотне$y = e^x$. Тому, використовуючи наші стандартні позначення, нехай$f(x) = e^x$ і$g(x) = \ln x$. Бажаємо знайти$g^\prime (x)$. Теорема 22 дає:

$$\begin{align*} g^\prime (x) &= \frac{1}{f^\prime(g(x))} \\ &= \frac{1}{e^{\ln x}} \\ &= \frac{1}{x}. \end{align*}$$

У цьому розділі ми визначили похідну, дали правила для полегшення її обчислення та дали похідні ряду стандартних функцій. Ми повторюємо найважливіші з них у наступній теоремі, призначеної для подальшої роботи.

Теорема 24: Глосарій похідних елементарних функцій

$v$Дозволяти$u$ і бути диференційовні функції, і нехай$a$,$c$ і$n$ бути дійсними числами,$a>0$,$n\neq 0$.