1.E: Застосування обмежень (вправи)

1.1: Вступ до обмежень

Терміни та поняття

1. За вашими власними словами, що означає «знайти межу$f(x)$ як$x$ наближається 3»?
2. Вираз форми$\frac00$ називається _____.
3. T/F: Межа$f(x)$ як$x$ наближається 5 є$f(5)$.
4. Опишіть три ситуації, коли$\lim\limits_{x\to c}f(x)$ не існує.
5. За вашими власними словами, що таке коефіцієнт різниці.

Проблеми

У вправах 6-16 наближають задані межі як чисельно, так і графічно.

6. $\lim\limits_{x\to 1}x^2+3x-5$

7. $\lim\limits_{x\to 0}x^3-3x^2+x-5$

8. $\lim\limits_{x\to 0}\frac{x+1}{x^2+3x}$

9. $\lim\limits_{x\to 3}\frac{x^2-2x-3}{x^2-4x+3}$

10. $\lim\limits_{x\to-1}\frac{x^2+8x+7}{x^2+6x+5}$

11. $\lim\limits_{x\to 2}\frac{x^2+7x+10}{x^2-4x+4}$

12. $\lim\limits_{x\to 2}$, де$f(x) = \begin{cases}x+2 \quad x\le 2\\ 3x-5 \quad x>2 \end{cases}.$

13. $\lim\limits_{x\to 3}$, де$f(x) = \begin{cases}x^2-x+1 \quad & x\le 3\\ 2x+1 &x>3 \end{cases}.$

14. $\lim\limits_{x\to 0}$, де$f(x) = \begin{cases}\cos x \quad & x\le 0\\ x^2+3x+1 &x>0 \end{cases}.$

15. $\lim\limits_{x\to \pi/2}$, де$f(x) = \begin{cases}\sin x \quad & x\le \pi/2\\ \cos x &x>\pi/2 \end{cases}.$

У вправах 16-24 задано функцію$f$$a$ і значення. Орієнтовна межа різницевого коефіцієнта$\lim\limits_{h\to 0}\frac{f(a+h)-f(a)}{h}$, використовуючи$h=\pm 0.1,\, \pm 0.01.$

16. $f(x)=-7x+2,\quad a=3$

17. $f(x)=9x+0.06,\quad a=-1$

18. $f(x)=x^2+3x-7,\quad a=1$

19. $f(x)=\frac{1}{x+1},\quad a=2$

20. $f(x)=-4x^2+5x-1,\quad a=-3$

21. $f(x)=\ln x,\quad a=5$

22. $f(x)=\sin x,\quad a=\pi$

23. $f(x)=\cos x,\quad a=\pi$

1.2: Визначення межі Епсілон-Дельта

Терміни та поняття

1. Що не так з наступним «визначенням» ліміту?

«Межа$f(x)$, як х наближається$a$,$K''$ означає, що враховуючи будь-яке$\delta >0$ існує$\epsilon >0$ таке, що всякий раз$|f(x)-K|<\epsilon$, коли, ми маємо$|x-a|<\delta$.

2. Що дається першим у встановленні межі, толерантності до x або толерантності у y?

3. T/F: завжди$\epsilon$ повинен бути позитивним.

4. T/F: завжди$\delta$ повинен бути позитивним.

Проблеми

У вправах 5-11 доведіть задану межу, використовуючи$\epsilon -\delta$ доказ.

5. $\lim\limits_{x\to5}3-x+-2$

6. $\lim\limits_{x\to3}x^2-3=6$

7. $\lim\limits_{x\to4}x^2+x-5=15$

8. $\lim\limits_{x\to2}x^3-1=7$

9. $\lim\limits_{x\to2}5=5$

10. $\lim\limits_{x\to0}e^{2x}-1=0$

11. $\lim\limits_{x\to0}\sin x = 0$(Підказка: використовуйте той факт, що$|\sin x |\le |x|,$ при рівності тільки тоді, коли$x=0$.)

1.3: Аналітичне знаходження меж

Терміни та поняття

1. Поясніть своїми словами, не використовуючи$ε-δ$ формальності, чому$\lim\limits_{x\to c}b=b$.

2. Поясніть своїми словами, не використовуючи$ε-δ$ формальності, чому$\lim\limits_{x\to c}x=c$.

3. Що означає текст, коли йдеться про те, що певні функції «поведінка «приємна» з точки зору обмежень»? Що, зокрема, «приємно»?

4. Намалюйте графік, який наочно демонструє теорему Стиснення.

5. Вам надається наступна інформація:

(а)$\lim\limits_{x\to1}f(x)=0$

(б)$\lim\limits_{x\to1}g(x)=0$

(c)$\lim\limits_{x\to1}f(x)/g(x) =2$

Що можна сказати про відносні розміри$f(x)$ і$g(x)$ як х наближається до 1?

Проблеми

Використання:

$$\begin{align}\lim\limits_{x\to9}f(x)=6 \qquad \lim\limits_{x\to6}f(x)=9 \\ \lim\limits_{x\to9}g(x)=3 \qquad \lim\limits_{x\to6}g(x)=3 \end{align}$$

оцінити межі, наведені у вправах 6-13, де це можливо. Якщо це неможливо дізнатися, констатуйте так.

6. $\lim\limits_{x\to9}(f(x)+g(x))$

7. $\lim\limits_{x\to9}(3f(x)/g(x))$

8. $\lim\limits_{x\to9} \left ( \frac{f(x)-2g(x)}{g(x)}\right )$

9. $\lim\limits_{x\to6}\left (\frac{f(x)}{3-g(x)}\right )$

10. $\lim\limits_{x\to9}g(f(x))$

11. $\lim\limits_{x\to6}f(g(x))$

12. $\lim\limits_{x\to6}g(f(f(x)))$

13. $\lim\limits_{x\to6}f(x)g(x)-f^2(x)+g^2(x)$

Використання

$$\begin{align}\lim\limits_{x\to1}f(x)=2 \qquad \lim\limits_{x\to10}f(x)=1 \\ \lim\limits_{x\to1}g(x)=0 \qquad \lim\limits_{x\to10}g(x)=\pi \end{align}$$

оцінити межі, наведені у вправах 14-17, де це можливо. Якщо це неможливо дізнатися, констатуйте так.

14. $\lim\limits_{x\to1}f(x)^{g(x)}$

15. $\lim\limits_{x\to10}\cos (g(x))$

16. $\lim\limits_{x\to1}f(x)g(x)$

17. $\lim\limits_{x\to1}g(5f(x))$

У вправах 18-32 оцініть заданий ліміт.

18. $\lim\limits_{x\to3}x^2-3x+7$

19. $\lim\limits_{x\to\pi}\left ( \frac{x-3}{x+5}\right )^7$

20. $\lim\limits_{x\to\pi /4}\cos x \sin x$

21. $\lim\limits_{x\to 0}\ln x$

22. $\lim\limits_{x\to3}4^{{x^3}-8x}$

23. $\lim\limits_{x\to\pi/6}\csc x$

24. $\lim\limits_{x\to0}\ln (1+x)$

25. $\lim\limits_{x\to\pi}\frac{x^2+3x+5}{5x^2-2x-3}$

26. $\lim\limits_{x\to\pi}\frac{3x+1}{1-x}$

27. $\lim\limits_{x\to6}\frac{x^2-4x-12}{x^2-13x+42}$

28. $\lim\limits_{x\to0}\frac{x^2+2x}{x^2-2x}$

29. $\lim\limits_{x\to2}\frac{x^2+6x-16}{x^2-3x+2}$

30. $\lim\limits_{x\to2}\frac{x^2-5x-14}{x^2+10x+16}$

31. $\lim\limits_{x\to-2}\frac{x^2-5x-14}{x^2+10x+16}$

32. $\lim\limits_{x\to-1}\frac{x^2+9x+8}{x^2-6x-7}$\

Використовуйте теорему стискання у вправах 33-36, де це доречно, для оцінки заданої межі.

33. $\lim\limits_{x\to0} x\sin \left (\frac{1}{x}\right )$

34. $\lim\limits_{x\to0}\sin x \cos \left ( \frac{1}{x^2}\right )$

35. $\lim\limits_{x\to1}f(x)$, де$3x-2\le f(x)\le x^3.$

36. $\lim\limits_{x\to3+}f(x),$де$6x-9\le f(x)\le x^2$ на [0,3].

Вправи 37-40, киньте виклик розумінню обмежень, але їх можна оцінити, використовуючи знання, отримані в цьому розділі.

37. $\lim\limits_{x\to0}\frac{\sin 3x}{x}$

38. $\lim\limits_{x\to0}\frac{\sin 5x}{8x}$

39. $\lim\limits_{x\to0}\frac{\ln (1+x)}{x}$

40. $\lim\limits_{x\to0}\frac{\sin x}{x}$, Де x вимірюється в градусах, а не радіанах.

1.4: Односторонні межі

Терміни та поняття

1. Які три способи обмеження може не існувати?

2. T/F: Якщо$\lim\limits_{x\to1-}f(x)=5$, то$\lim\limits_{x\to1}f(x)=5$

3. T/F: Якщо$\lim\limits_{x\to1-}f(x)=5$, то$\lim\limits_{x\to1+}f(x)=5$

4. T/F: Якщо$\lim\limits_{x\to1}f(x)=5$, то$\lim\limits_{x\to1-}f(x)=5$

Проблеми

У вправах 5-12 оцінюйте кожен вираз, використовуючи заданий графік$f(x)$.

5.

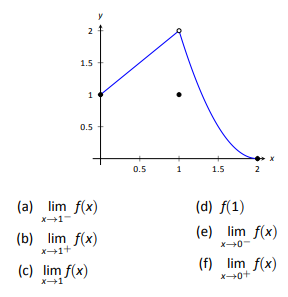
6.

7.

8.

9.

10.

11.

12.

У вправах 13-21 оцініть задані межі кусково визначених функцій$f$.

13. $f(x) = \begin{cases} x+1 \quad &x\le 1\\ x^2-5 &x>1 \end{cases}$
(а)$\lim\limits_{x\to1^-}f(x)$
(б)$\lim\limits_{x\to0^+}f(x)$
(с)$\lim\limits_{x\to1}f(x)$
(г)$f(1)$

14. $f(x) = \begin{cases} 2x^2+5x-1 \quad &x<0 \\ \sin x &x\ge 0 \end{cases}$
(а)$\lim\limits_{x\to0^-}f(x)$
(б)$\lim\limits_{x\to0^+}f(x)$
(с)$\lim\limits_{x\to0}f(x)$
(г)$f(0)$

15. $f(x) = \begin{cases} x^-1 \quad &x<-1 \\ x^3+1 &-1\le x \le 1 \\ x^2+1 &x>1 \end{cases}$
(а)$\lim\limits_{x\to-1^-}f(x)$
(б)$\lim\limits_{x\to1^+}f(x)$
(c)$\lim\limits_{x\to-1}f(x)$
(d)$f(-1)$
(е)$\lim\limits_{x\to1^-}f(x)$
(f)$\lim\limits_{x\to1^+}f(x)$
(г)$\lim\limits_{x\to1}f(x)$
(ч)$f(1)$

16. $f(x) = \begin{cases} \cos x \quad &x<\pi \\ \sin x &x\ge \pi \end{cases}$
(а)$\lim\limits_{x\to\pi^-}f(x)$
(б)$\lim\limits_{x\to\pi^+}f(x)$
(с)$\lim\limits_{x\to\pi}f(x)$
(г)$f(\pi)$

17. $f(x) = \begin{cases} 1-\cos ^2 x \quad &x<a \\ \sin^2 x &x\ge a \end{cases}$, Де$a$ - дійсне число.
(а)$\lim\limits_{x\to a^-}f(x)$
(б)$\lim\limits_{x\to a^+}f(x)$
(с)$\lim\limits_{x\to a}f(x)$
(г)$f(a)$

18. $f(x) = \begin{cases} x+1 \quad &x<1 \\ 1 &x=1 \\ x-1 &x>1 \end{cases}$
(а)$\lim\limits_{x\to1^-}f(x)$
(б)$\lim\limits_{x\to1^+}f(x)$
(с)$\lim\limits_{x\to1}f(x)$
(г)$f(1)$

19. $f(x) = \begin{cases} x^2 \quad &x<2 \\ x+1 &x=2 \\ -x^2+2x+4 &x>2 \end{cases}$
(а)$\lim\limits_{x\to2^-}f(x)$
(б)$\lim\limits_{x\to2^+}f(x)$
(с)$\lim\limits_{x\to2}f(x)$
(г)$f(2)$

20. $f(x) = \begin{cases} a(x-b)^2+c\quad &x<b \\ a(x-b)+c &x\ge b \end{cases}$, де a, b і c - дійсні числа.
(а)$\lim\limits_{x\to b^-}f(x)$
(б)$\lim\limits_{x\to b^+}f(x)$
(с)$\lim\limits_{x\to b}f(x)$
(г)$f(b)$

21. $f(x) = \begin{cases}\frac{|x|}{x} \quad &x\ne 0 \\ 0 &x= 0 \end{cases}$
(а)$\lim\limits_{x\to0^-}f(x)$
(б)$\lim\limits_{x\to0^+}f(x)$
(с)$\lim\limits_{x\to0}f(x)$
(г)$f(0)$

Рецензія

22. Оцініть ліміт:$\lim\limits_{x\to -1}\frac{x^2+5x+4}{x^2-3x-4}$

23. Оцініть ліміт:$\lim\limits_{x\to -4}\frac{x^2-16}{x^2-4x-32}$

24. Оцініть ліміт:$\lim\limits_{x\to -6}\frac{x^2-15x+54}{x^2-6x}$

25. Приблизний межа чисельно:$\lim\limits_{x\to 0.4}\frac{x^2-4.4x+1.6}{x^2-0.4x}$

26. Приблизний межа чисельно:$\lim\limits_{x\to 0.2}\frac{x^2+5.8x-1.2}{x^2-4.2x+0.8}$

1.5: Безперервність

Терміни та поняття

1. Своїми словами опишіть, що означає, щоб функція була безперервною.

2. Своїми словами опишіть, що говорить теорема про проміжні значення.

3. Що таке «корінь» функції?

4. Задані функції$f\text{ and }g$ на інтервалі$I$, як можна використовувати метод бісекції, щоб знайти значення c де$f(c) = g(c)$?

5. T/F: Якщо$f$ визначається на відкритому інтервалі, що містить c, і$\lim\limits_{x\to c} f(x)$ існує, то$f$ є безперервним при c.

6. T/F: Якщо$f$ є безперервним при c, то$\lim\limits_{x\to c} f(x)$ існує

7. T/F: Якщо$f$ безперервний при c, то$\lim\limits_{x\to c^+} f(x)=f(c)$.

8. T/F: Якщо$f$ є безперервним на [a, b], то$\lim\limits_{x\to a^-} f(x)=f(a)$.

9. T/F: Якщо f є безперервним на [0, 1) і [1, 2), то$f$ є безперервним на [0, 2).

10. T/F: Сума неперервних функцій також є безперервною.

Проблеми

У вправах 11-17 разом зі значенням$f$ дається графік функції$a$. Визначте$f$, чи є безперервним при$a$; якщо це не так, вкажіть, чому це не так.

11. $a=1$

12. $a=1$

13. $a=1$

14. $a=0$

15. $a=1$

16. $a=4$

17.
(а)$a=-2$
(б)$a=0$
(с)$a=2$

У вправах 18-21 визначте, чи$f$ є безперервним при зазначених значеннях. Якщо ні, поясніть, чому.

18. $f(x) = \begin{cases} 1 \quad &x=0\\ \frac{\sin x}{x} &x>0 \end{cases}$
(а)$x=0$
(б)$x=\pi$

19. $f(x) = \begin{cases} x^3-x \quad &x<1\\ x-2 &x\ge 1 \end{cases}$
(а)$x=0$
(б)$x=1$

20. $f(x) = \begin{cases} \frac{x^2+5x+4}{x^2 +3x+2} \quad &x\ne -1\\ 3 &x=-1 \end{cases}$
(а)$x=-1$
(б)$x=10$

21. $f(x) = \begin{cases} \frac{x^2-64}{x^2-11x+24} \quad &x\ne 8\\ 5 &x=8 \end{cases}$
(а)$x=0$
(б)$x=8$

У вправах 22-32 дайте інтервали, на яких дана функція безперервна.

22. $f(x)=x^2-3x+9$

23. $g(x) = \sqrt{x^2-4}$

24. $h(k) = \sqrt{1-k}+\sqrt{k+1}$

25. $f(t) = \sqrt{5t^2-30}$

26. $g(t) = \frac{1}{\sqrt{1-t^2}}$

27. $g(x) = \frac{1}{1+x^2}$

28. $f(x) = e^x$

29. $g(s) = \ln s$

30. $h(t) = \cos t$

31. $f(k) = \sqrt{1-e^k}$

32. $f(x) = \sin (e^x+x^2)$

33. $f$Дозволяти бути безперервним на [1,5] де$f(1) = -2 \text{ and }f(5)=-10$. Чи$1<c<5$ існує таке значення$f(c)=-9$? Чому б і ні?

34. $g$Дозволяти бути безперервним на [-3,7] де$g(0)=0 \text{ and }g(2)=25$. Чи$-3<c<7$ існує таке значення, що$g(c)=15?$ чому/чому б і ні?

35. $f$Дозволяти бути безперервним на [-1,1] де$f(-1)=-10 \text{ and }f(1)=10$. Чи$-1<c<1$ існує таке значення, що$f(c)=11?$ чому/чому б і ні?

36. $h$Дозволяти бути безперервним на [-1,1] де$h(-1)=-10 \text{ and }h(1)=10$. Чи$-1<c<1$ існує таке значення, що$h(c)=0?$ чому/чому б і ні?

У вправах 37-40 використовуйте метод бісекції для наближення, з точністю до двох знаків після коми, значення кореня заданої функції в заданому інтервалі.

37. $f(x) = x^2+2x-4\text{ on }[1,1.5]$.

38. $f(x) = \sin x -1/2\text{ on }[0.5,0.55]$.

39. $f(x) = e^x-2\text{ on }[0.65,0.7]$.

40. $f(x) = \cos x -\sin x \text{ on }[0.7,0.8]$.

Рецензія

41. Нехай$f(x) = \begin{cases} x^2-5 \quad &x<5\\ 5x &x\ge 5 \end{cases}$.
(а)$\lim\limits_{x\to 5^-}f(x)$
(б)$\lim\limits_{x\to 5^+}f(x)$
(с)$\lim\limits_{x\to 5}f(x)$
(г)$f(5)$

42. Чисельно наближаються наступні межі:
(a)$\lim\limits_{x\to 4/5^+}\frac{x^2-8.2x-7.2}{x^2+5.8x+4}$
(b)$\lim\limits_{x\to 4/5^-}\frac{x^2-8.2x-7.2}{x^2+5.8x+4}$

43. Наведіть приклад функції,$f(x)$ для якої$\lim\limits_{x\to 0}f(x)$ не існує.

1.6: Межі за участю нескінчен

Терміни та поняття

1. T/F: Якщо$\lim\limits_{x\to 5}f(x)=\infty$, то ми неявно заявляємо, що межа існує.

2. T/F: Якщо$\lim\limits_{x\to \infty}f(x)=5$, то ми неявно заявляємо, що межа існує.

3. T/F: Якщо$\lim\limits_{x\to 1^-}f(x)=-\infty$, то$\lim\limits_{x\to 1^+}f(x)=\infty$.

4. T/F: Якщо$\lim\limits_{x\to 5}f(x)=\infty$, то$f$ має вертикальну асимптоту при$x=5$.

5. T/F: не$\infty/0$ є невизначеною формою.

6. Перерахуйте 5 невизначених форм.

7. Побудувати функцію з вертикальною асимптотою при x = 5 і горизонтальною асимптотою при y = 5.

8. Нехай$\lim\limits_{x\to 7}f(x)=\infty$. Поясніть, як ми знаємо,$f$ що є/не є безперервним в$x=7$.

Проблеми

У вправах 9-14 оцініть задані межі за допомогою графіка функції.

9. $f(x) = \frac{1}{(x+1)^2}$
(а)$\lim\limits_{x\to -1^-}f(x)$
(б)$\lim\limits_{x\to -1^+}f(x)$

10. $f(x) = \frac{1}{(x-3)(x-5)^2}$
(а)$\lim\limits_{x\to 3^-}f(x)$
(б)$\lim\limits_{x\to 3^+}f(x)$
(c)$\lim\limits_{x\to 3}f(x)$
(d)$\lim\limits_{x\to 5^-}f(x)$
(е)$\lim\limits_{x\to 5^+}f(x)$
(f)$\lim\limits_{x\to 5}f(x)$

11. $f(x) = \frac{1}{e^x+1}$
(а)$\lim\limits_{x\to -\infty}f(x)$
(б)$\lim\limits_{x\to \infty}f(x)$
(с)$\lim\limits_{x\to 0^-}f(x)$
(г)$\lim\limits_{x\to 0^+}f(x)$

12. $f(x) = x^2\sin (\pi x)$
(а)$\lim\limits_{x\to -\infty}f(x)$
(б)$\lim\limits_{x\to \infty}f(x)$

13. $f(x)=\cos (x)$
(а)$\lim\limits_{x\to -\infty}f(x)$
(б)$\lim\limits_{x\to \infty}f(x)$

14. $f(x) = 2^x +10$
(а)$\lim\limits_{x\to -\infty}f(x)$
(б)$\lim\limits_{x\to \infty}f(x)$

У вправах 15-18 чисельно наближають наступні межі:
(a)$\lim\limits_{x\to 3^-}f(x)$
(b)$\lim\limits_{x\to 3^+}f(x)$
(c)$\lim\limits_{x\to 3}f(x)$

15. $f(x) = \frac{x^2-1}{x^2-x-6}$

16. $f(x) = \frac{x^2+5x-36}{x^3-5x^2+3x+9}$

17. $f(x) = \frac{x^2-11x+30}{x^3-4x^2-3x+18}$

18. $f(x) = \frac{x^2-9x+18}{x^2-x-6}$

У вправах 19-24 визначте горизонтальні та вертикальні асимптоти, якщо такі є, заданої функції.

19. $f(x) = \frac{2x^2-2x-4}{x^2+x-20}$

20. $f(x) = \frac{-3x^2-9x-6}{5x^2-10x-15}$

21. $f(x) = \frac{x^2+2-12}{7x^3-14x^2-21x}$

22. $f(x) = \frac{x^2-9}{9x-9}$

23. $f(x) = \frac{x^2-9}{9x+27}$

24. $f(x) = \frac{x^2-1}{-x^2-1}$

У вправах 25-28 оцініть заданий ліміт.

25. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{x-5}$

26. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{5-x}$

27. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{x^2-5}$

28. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{5-x^2}$

Рецензія

29. Використовуйте$ε − δ$ доказ, щоб показати це$\lim\limits_{x\to 1}5x-2=3$.

30. Нехай$\lim\limits_{x\to 2}f(x)=3\text{ and }\lim\limits_{x\to 2}g(x)=-1$. Оцініть наступні межі.
(а)$\lim\limits_{x\to 2}(f+g)(x)$
(б)$\lim\limits_{x\to 2}(fg)(x)$
(с)$\lim\limits_{x\to 2}(f/g)(x)$
(г)$\lim\limits_{x\to 2}f(x)^{g(x)}$

31. Нехай$f(x) = \begin{cases}x^2-1 \qquad &x<3 \\ x+5 &x \ge 3 \end{cases}$. Чи скрізь$f$ безперервно?

32. Оцініть ліміт:$\lim\limits_{x\to c}\ln x$.