1.4: Односторонні межі

Last updated
Save as PDF

Page ID: 60783

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми ввели поняття межі м'яко, наближаючи їх значення графічно і чисельно. Далі йшло суворе визначення межі разом з, за загальним визнанням, стомлюючим методом їх оцінки. Попередній розділ дав нам інструменти (які ми називаємо теоремами), які дозволяють нам обчислювати межі з більшою легкістю. Головними серед результатів були факти, що поліноми та раціональні, тригонометричні, експоненціальні та логарифмічні функції (а також їх суми, добуток тощо) поводяться «красиво». У цьому розділі ми чітко визначаємо, що ми маємо на увазі під «красиво».

У розділі 1.1 ми досліджували три способи, за яких межі функцій не існували:

Функція наближалася до різних значень зліва і справа,
Функція зростає без обмежень, і
Функція коливається.

У цьому розділі ми детально досліджуємо концепції #1, вводячи односторонній ліміт. Почнемо з формальних визначень, які дуже схожі на визначення межі, наведеного в розділі 1.2, але позначення дещо інше і$x\neq c$ "" замінюється або$x<c$ "" або "$x>c$.

Визначення 2: Односторонні межі

Ліва межа

$I$Дозволяти бути відкритий інтервал$c$, що містить, і нехай$f$ бути функція визначена на$I$, крім можливо в$c$. Межа$f(x)$, як$x$ підходи$c$ зліва, є$L$, або, ліворучна$c$ межа$f$ at$L$, позначається

\[ \lim\limits_{x\rightarrow c^-} f(x) = L,\]

означає, що даний будь-який$\epsilon > 0$, існує$\delta > 0$ таке, що для всіх$x< c$, якщо$|x - c| < \delta$, то$|f(x) - L| < \epsilon$.

Праворуч межа

$I$Дозволяти бути відкритий інтервал$c$, що містить, і нехай$f$ бути функція визначена на$I$, крім можливо в$c$. Межа$f(x)$, як$x$$c$ наближається справа, є$L$, або, праворучна межа$f$ at$c$ є$L$, позначається

\[ \lim\limits_{x\rightarrow c^+} f(x) = L,\]

означає, що даний будь-який$\epsilon > 0$, існує$\delta > 0$ таке, що для всіх$x> c$, якщо$|x - c| < \delta$, то$|f(x) - L| < \epsilon$.

Практично кажучи, при оцінці лівої межі ми розглядаємо тільки значення$x$ «зліва від»$c$, тобто де$x<c$. За загальним визнанням недосконале позначення$x\to c^-$ використовується для того, щоб мати на увазі, що ми дивимося$x$ на значення зліва від$c$. Позначення не має нічого спільного з позитивними або від'ємними значеннями$x$ або$c$. Аналогічне твердження має місце для оцінки правосторонніх меж; там ми розглядаємо тільки значення$x$ праворуч від$c$, тобто$x>c$. Ми можемо використовувати теореми з попередніх розділів, щоб допомогти нам оцінити ці межі; ми просто обмежуємо наш погляд однією стороною$c$.

Ми практикуємо оцінку лівої та правої меж на низці прикладів.

Приклад 17: Оцінка односторонніх обмежень

Нехай$ f(x) = \left\{\begin{array}{cc} x & 0\leq x\leq 1 \\ 3-x & 1<x<2\end{array},\right.$, як показано на малюнку 1.21. Знайдіть кожне з наступних дій:

$\lim\limits_{x\to 1^-} f(x)$
$\lim\limits_{x\to 1^+} f(x)$
$\lim\limits_{x\to 1} f(x)$
$f(1)$
$\lim\limits_{x\to 0^+} f(x) $
$f(0)$
$\lim\limits_{x\to 2^-} f(x)$
$f(2)$

$альт$
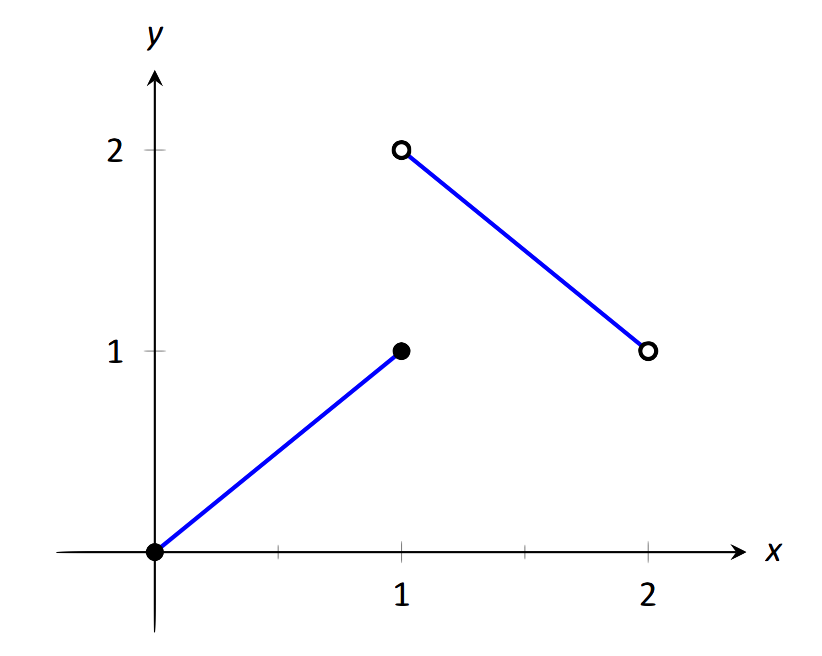
$\text{FIGURE 1.21}$: Графік$f$ у прикладі 17.

Рішення

Для цих проблем наочний посібник графіка, швидше за все, ефективніше оцінює межі, ніж використання$f$ самого себе. Тому ми будемо часто посилатися на графік.

Як$x$ переходить до 1 зліва, ми бачимо, що$f(x)$ наближається до значення 1. Тому$ \lim\limits_{x\to 1^-} f(x) =1.$
Як$x$ переходить до 1 справа, ми бачимо, що$f(x)$ наближається до значення 2. Нагадаємо, що не важливо, що там є «відкрите коло», ми оцінюємо межу, а не значення функції. Тому$ \lim\limits_{x\to 1^+} f(x)=2$.
Межі$f$ як$x$ підходів 1 не існує, про що йшлося в першому розділі. Функція наближається не до одного конкретного значення, а до двох різних значень зліва і справа.
Використовуючи визначення та дивлячись на графік, ми бачимо, що$f(1) = 1$.
Як$x$ йде до 0 праворуч, ми бачимо, що$f(x)$ також наближається 0. Тому$ \lim\limits_{x\to 0^+} f(x)=0$. Зауважте, що ми не можемо розглядати ліву межу в 0$f$, як не визначено для значень$x<0$.
Використовуючи визначення і графік,$f(0) = 0$.
Як$x$ переходить до 2 зліва, ми бачимо, що$f(x)$ наближається до значення 1. Тому$ \lim\limits_{x\to 2^-} f(x)=1.$
Графік і визначення функції показують,$f(2)$ що не визначено.

Зверніть увагу, як ліві та праві межі відрізнялися на$x=1$. Це, звичайно, призводить до того, що межі не існує. Наступна теорема стверджує, що є досить інтуїтивним: межа існує саме тоді, коли ліва та права межі рівні.

Теорема 7: Межі та односторонні межі

$f$Дозволяти функція, визначена на відкритому інтервалі,$I$ що містить$c$. Тоді\[\lim\limits_{x\to c}f(x) = L\] якщо, і тільки якщо,\[\lim\limits_{x\to c^-}f(x) = L \quad \text{and} \quad \lim\limits_{x\to c^+}f(x) = L.\]

Фраза «if, і only if» означає, що два твердження рівнозначні: вони або істинні, або обидва хибні. Якщо межа дорівнює$L$, то ліва і права рука обмежує обидві рівні$L$. Якщо межа не дорівнює$L$, то хоча б одна з лівих і правих меж не дорівнює$L$ (її може навіть не існувати).

Одна річ, яку слід враховувати в прикладах 17 - 20, полягає в тому, що значення функції можеть/не дорівнювати значенню (-ям) її лівої/правої межі, навіть коли ці межі узгоджуються.

Приклад 18: Оцінка меж кусково визначеної функції

Нехай$f(x) = \left\{\begin{array}{cc} 2-x & 0<x<1 \\ (x-2)^2 & 1<x<2 \end{array},\right.$, як показано на малюнку 1.22. Оцініть наступне.

$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$ f(1)$
$ \lim\limits_{x\to 0^+} f(x)$
$f(0)$
$ \lim\limits_{x\to 2^-} f(x)$
$f(2)$

$альт$
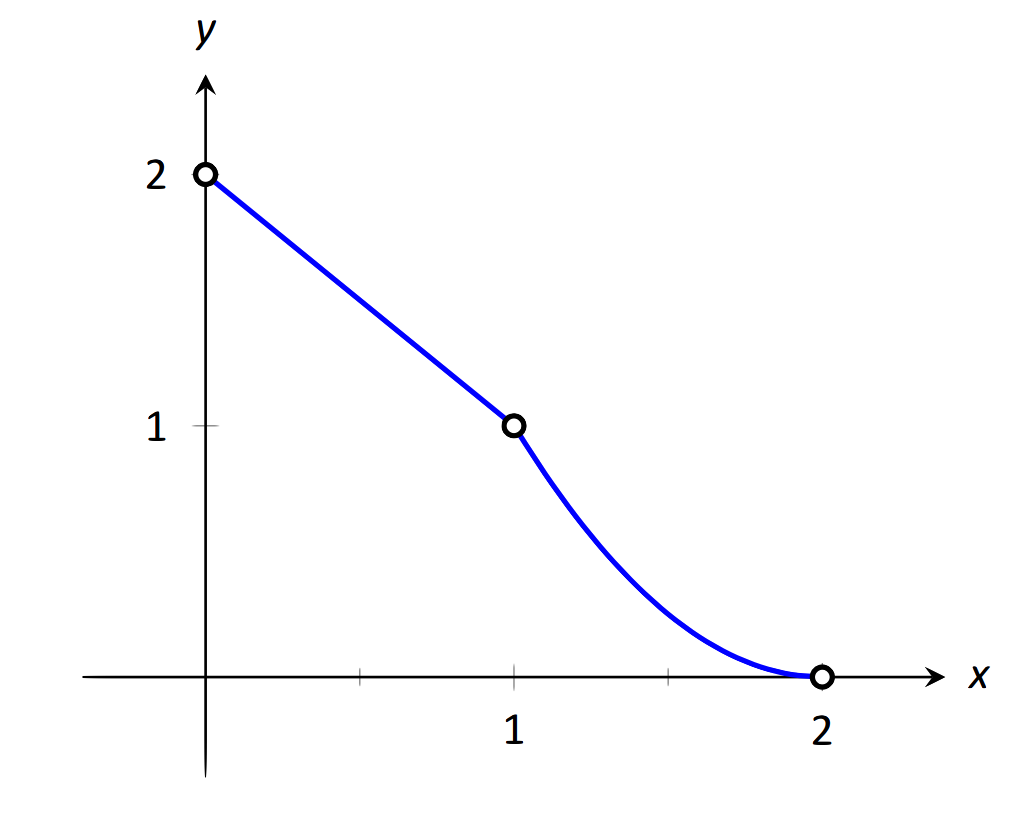
$\text{FIGURE 1.22}$: Графік$f$ з Прикладу 18.

Рішення

Знову ми оцінимо кожен, використовуючи як визначення, так$f$ і його графік.

Як$x$ наближається 1 зліва, ми бачимо, що$f(x)$ наближається до 1. Тому$ \lim\limits_{x\to 1^-} f(x)=1.$
Як$x$ наближається 1 справа, ми бачимо, що знову$f(x)$ наближається до 1. Тому$ \lim\limits_{x\to 1+} f(x)=1$.
Межа$f$ як$x$ підходів 1 існує і дорівнює 1, оскільки$f$ підходи 1 як праворуч, так і зліва. Тому$ \lim\limits_{x\to 1} f(x)=1$.
$f(1)$не визначено. Зверніть увагу, що 1 не знаходиться в області$f$, визначеної задачею, яка позначається на графіку відкритим колом при$x=1$.
Як$x$ переходить до 0 праворуч,$f(x)$ наближається до 2. Отже$ \lim\limits_{x\to 0^+} f(x)=2$.
$f(0)$не визначено як не$0$ знаходиться у домені$f$.
Як$x$ переходить до 2 зліва,$f(x)$ наближається до 0. Отже$ \lim\limits_{x\to 2^-} f(x)=0$.
$f(2)$не визначається як 2 не знаходиться в домені$f$.

Приклад 19: Оцінка меж кусково визначеної функції

Нехай$f(x) = \left\{\begin{array}{cc} (x-1)^2 & 0\leq x\leq 2, x\neq 1\\ 1 & x=1\end{array},\right.$, як показано на малюнку 1.23. Оцініть наступне.

$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$

$альт$
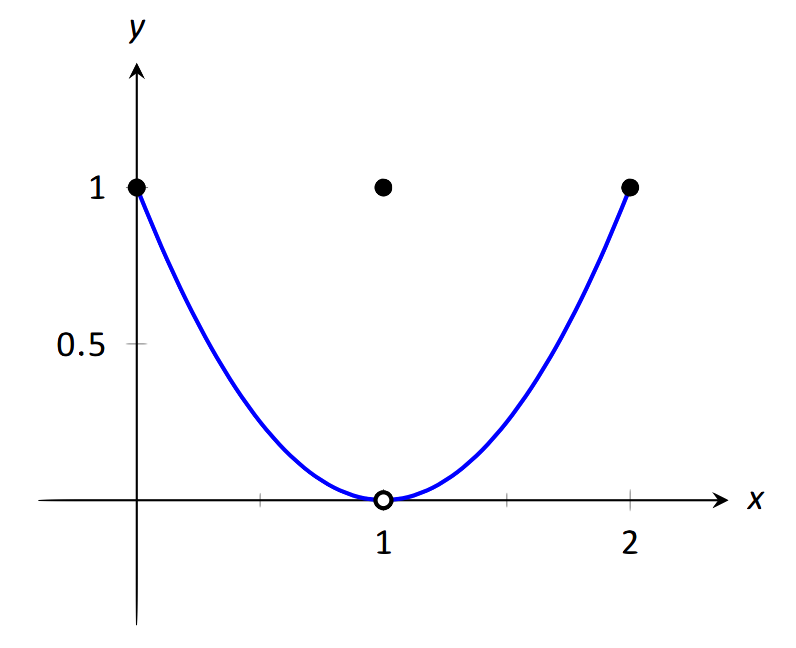
$\text{FIGURE 1.23}$: Графік$f$ у прикладі 19.

Подивившись на графік, зрозуміло, що як ліва, так і права межі$f$, як$x$ наближається до 1, дорівнює 0. Таким чином, також зрозуміло, що межа дорівнює 0; т$ \lim\limits_{x\to 1} f(x) = 0$. Е. Також чітко зазначено, що$f(1) = 1$.

Приклад 20: Оцінка меж кусково визначеної функції

Нехай$f(x) = \left\{\begin{array}{cc} x^2 & 0\leq x\leq 1 \\ 2-x & 1<x\leq 2\end{array},\right.$, як показано на малюнку 1.24. Оцініть наступне.

$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$

$альт$
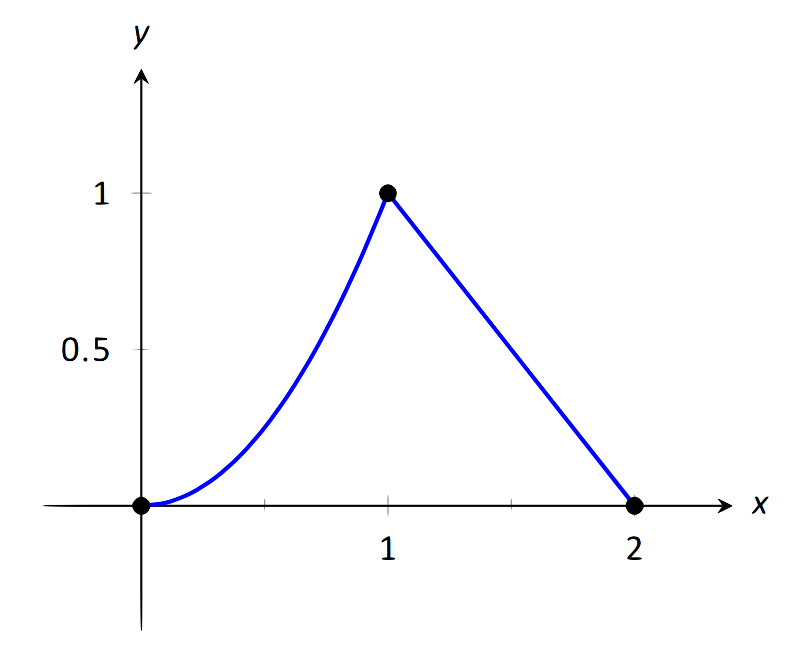
$\text{FIGURE 1.24}$: Графік$f$ у прикладі 20.

Рішення

З визначення функції і її графіка зрозуміло, що всі перераховані нижче рівні:

\[\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^+} f(x) =\lim\limits_{x\to 1} f(x) =f(1) = 1.\]

У прикладах 17 - 20 нас попросили знайти обидва$ \lim\limits_{x\to 1}f(x)$ і$f(1)$. Розглянемо наступну таблицю:

\[\begin{array}{ccc} & \lim\limits_{x\to 1}f(x) & f(1) \\ \hline \text{Example 17} & \text{does not exist} & 1 \\ \text{Example 18} & 1 & \text{not defined} \\ \text{Example 19} & 0 & 1 \\ \text{Example 20} & 1 & 1 \\ \end{array}\]

Тільки в прикладі 20 існують і функції, і ліміт і згодні. Це здається «приємним»; насправді це здається «нормальним». Насправді це важлива ситуація, яку ми досліджуємо в наступному розділі під назвою «Безперервність». Коротше кажучи, безперервна функція - це та, в якій, коли функція наближається до значення як$x\rightarrow c$ (тобто коли$ \lim\limits_{x\to c} f(x) = L$), вона насправді досягає цього значення в$c$. Такі функції поводяться красиво, оскільки вони дуже передбачувані.

Автори та авторства

Template:ContribApexCalc