1.6: Межі за участю нескінчен

Last updated
Save as PDF

Page ID: 60790

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У Визначенні 1 ми заявили, що в$ \lim\limits_{x\to c}f(x) = L$ рівнянні обидва$c$ і$L$ були числами. У цьому розділі ми трохи розслабляємо це визначення, розглядаючи ситуації, коли має сенс дозволити$c$ та/або$L$ бути «нескінченністю».

Як мотивуючий приклад розглянемо$f(x) = 1/x^2$, як показано на малюнку 1.30. Зверніть увагу, як,$x$ наближаючись до 0,$f(x)$ зростає дуже-дуже великий. Здається доречним і описовим, щоб заявити, що\[\lim\limits_{x\rightarrow 0} \frac1{x^2}=\infty.\] Також зверніть увагу, що як$x$ стає дуже великим,$f(x)$ стає дуже, дуже маленьким. Ми могли б представити це поняття за допомогою таких позначень, як\[\lim\limits_{x\rightarrow \infty} \frac1{x^2}=0.\]

$альт$
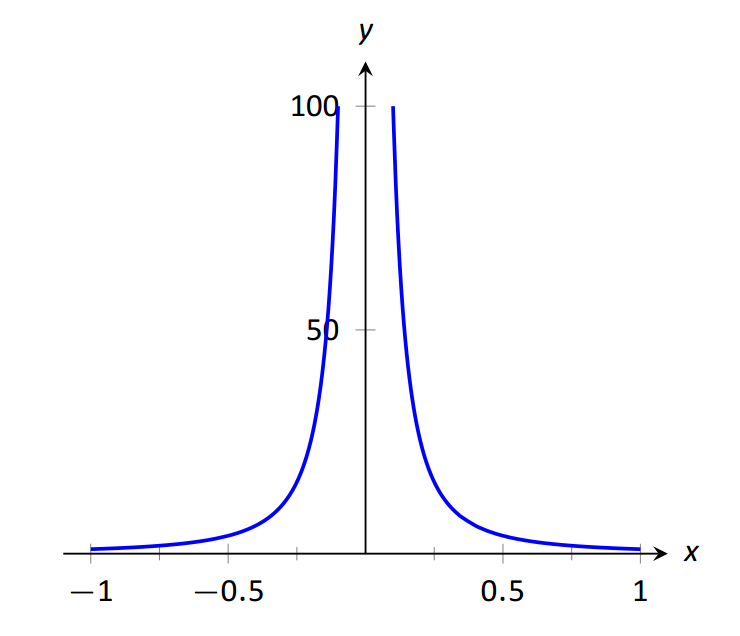
$\text{FIGURE 1.30}$: Графік$f(x)=1/x^2$ для значень$x \text{ near }0$.

Ми досліджуємо обидва види використання по$\infty$ черзі.

Визначення 5: Межа нескінченності

Ми говоримо,$ \lim\limits_{x\rightarrow c} f(x)=\infty$ якщо для кожного$M>0$ існує$\delta>0$ таке, що для всіх$x\neq c$, якщо$|x-c|<\delta$, то$f(x)\geq M$.

Це так само, як$\epsilon$ -$\delta$ визначення з розділу 1.2. У цьому визначенні, задано будь-яке (мале) значення$\epsilon$, якщо ми дозволимо$x$ отримати досить близько до$c$ (в межах$\delta$ одиниць$c$),$f(x)$ то гарантовано буде в межах$\epsilon$$f(c)$. Тут, враховуючи будь-яке (велике) значення$M$, якщо ми дозволимо$x$ отримати досить близько до$c$ (в межах$\delta$ одиниць$c$), то$f(x)$ буде принаймні такий же великий, як$M$. Іншими словами, якщо ми підійдемо досить близько до$c$, то ми можемо зробити$f(x)$ стільки, скільки хочемо. Ми можемо визначити межі,$-\infty$ рівні аналогічним чином.

Важливо зазначити, що, кажучи,$ \lim\limits_{x\to c}f(x) = \infty$ ми неявно заявляємо, що\ textit {the} межа$f(x)$, як$x$ підходів$c$, не існує. Обмеження існує лише тоді, коли$f(x)$ наближається до фактичного числового значення. Ми використовуємо поняття меж, які наближаються до нескінченності, оскільки воно корисне та описове.

Приклад 26: Оцінка меж за участю нескінченності

Знайдіть$ \lim\limits_{x\rightarrow 1}\frac1{(x-1)^2}$, як показано на малюнку 1.31.

$альт$
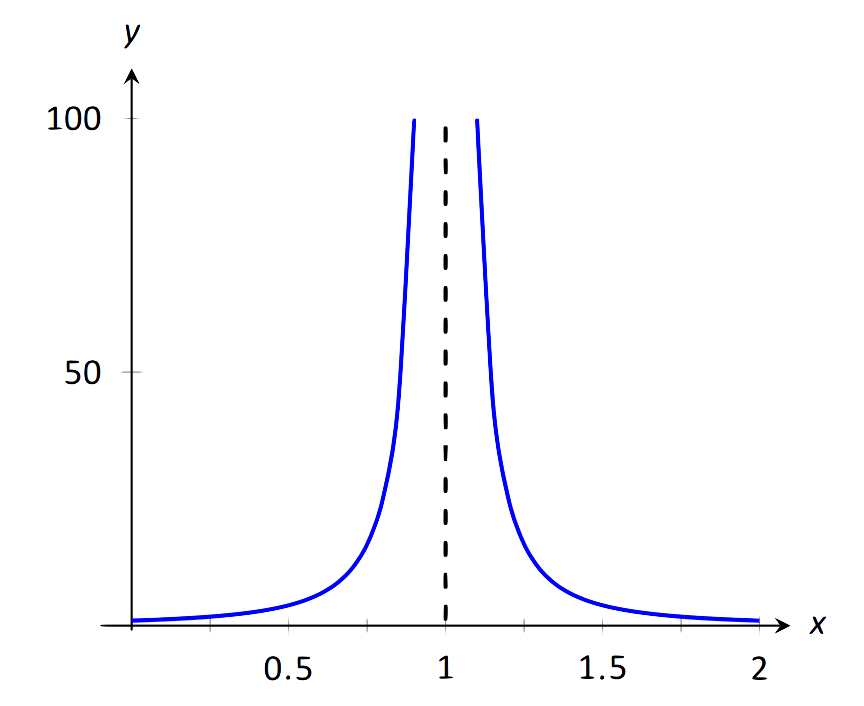
$\text{FIGURE 1.31}$: Дотримуючись нескінченну$x\to 1$ межу, як у прикладі 26.

Рішення

У прикладі 4 розділу 1.1, перевіряючи значення$x$ близьких до 1, ми дійшли висновку, що цієї межі не існує. Тобто він не може дорівнювати жодному дійсному числу. Але межа могла бути нескінченною. І насправді, ми бачимо, що функція, здається, зростає все більше і більше, як$f(.99)=10^4$,$f(.999)=10^6$,$f(.9999)=10^8$. Аналогічна річ відбувається з іншого боку 1. Загалом, нехай дається «велике» значення$M$. Нехай$\delta=1/\sqrt{M}$. Якщо$x$ знаходиться в межах$\delta$ 1, тобто якщо$|x-1|<1/\sqrt{M}$, то:

\[\begin{align*}|x-1| &< \frac{1}{\sqrt{M}} \\ (x-1)^2 &< \frac{1}{M}\\ \frac{1}{(x-1)^2} &> M,\end{align*}\]

це те, що ми хотіли показати. Так можна сказати$\lim\limits_{x\rightarrow 1}1/{(x-1)^2}=\infty$.

Приклад 27: Оцінка меж за участю нескінченності

Знайдіть$\lim\limits_{x\rightarrow 0}\frac1x$, як показано на малюнку 1.32.

$альт$
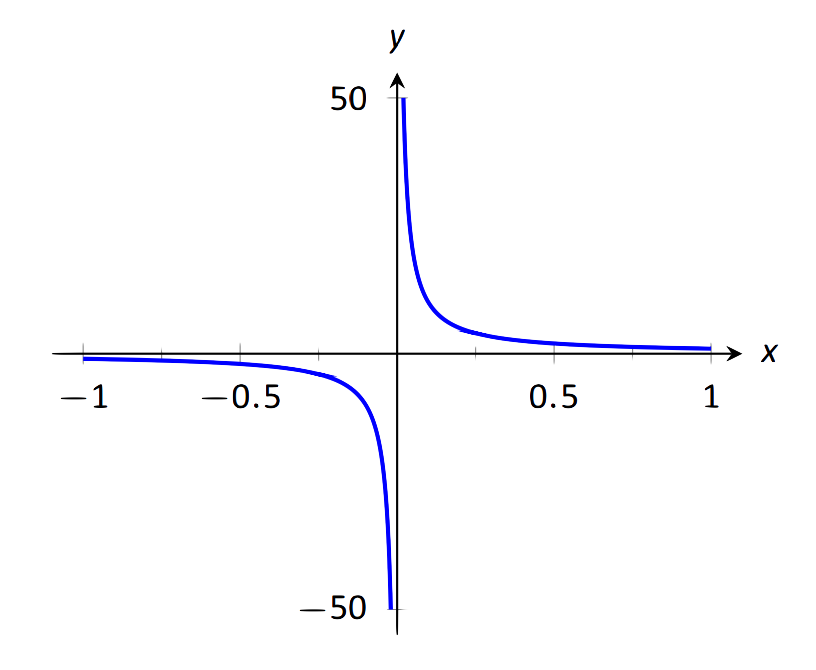
$\text{FIGURE 1.32}$: Оцінка$\lim\limits_{x\to 0}\frac{1}{x}$.

Рішення

Легко помітити, що функція зростає без обмежень біля 0, але вона робить це по-різному з різних сторін 0. Оскільки його поведінка не є послідовною, ми не можемо цього сказати$ \lim\limits_{x\to 0}\frac{1}{x}=\infty$. Однак ми можемо зробити заяву про односторонні межі. Ми можемо констатувати, що$ \lim\limits_{x\rightarrow 0^+}\frac1x=\infty$ і$ \lim\limits_{x\rightarrow 0^-}\frac1x=-\infty$.

Вертикальні асимптоти

Якщо$f(x)$ межа як$x$ наближається$c$ з лівого або правого (або обох) є$\infty$ або$-\infty$, ми говоримо, що функція має вертикальну асимптоту в$c$.

Приклад 28: Пошук вертикальних асимптотів

Знайти вертикальні асимптоти$f(x)=\dfrac{3x}{x^2-4}$.

$альт$
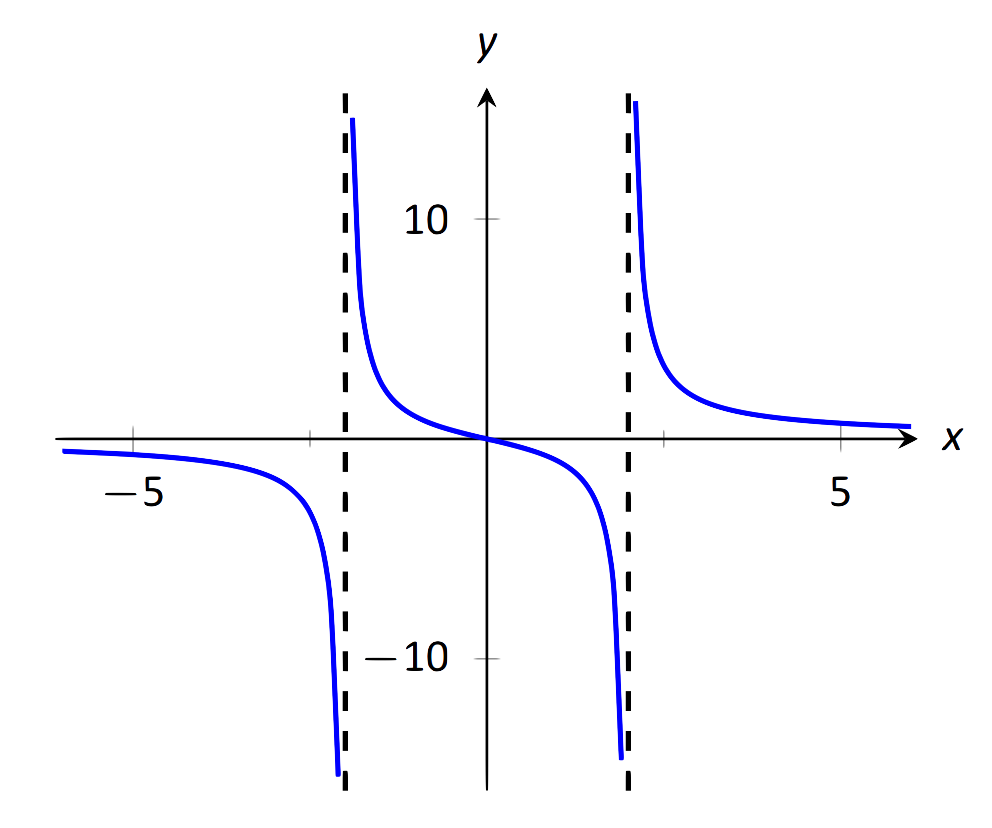
$\text{FIGURE 1.33}$: Графік$f(x) = \frac{3x}{x^2-4}$.

Рішення

Вертикальні асимптоти виникають там, де функція зростає без обмежень; це може відбуватися при значеннях,$c$ де знаменник дорівнює 0. Коли$x$ поруч$c$, знаменник невеликий, що в свою чергу може змусити функцію приймати великі значення. У випадку з заданою функцією знаменник дорівнює 0 at$x=\pm 2$. Заміна значень$x$ близьких до$2$ і,$-2$ здається, вказує на те, що функція прагне до$\infty$ або$-\infty$ в цих точках. Ми можемо графічно підтвердити це, подивившись на рисунок 1.33. Таким чином, вертикальні асимптоти знаходяться при$x=\pm2$.

Коли раціональна функція має вертикальну асимптоту at$x=c$, можна зробити висновок, що знаменник дорівнює 0 at$x=c$. Однак тільки тому, що знаменник дорівнює 0 в певній точці, не означає, що там існує вертикальна асимптота. Наприклад,$f(x)=(x^2-1)/(x-1)$ не має вертикальної асимптоти при$x=1$, як показано на малюнку 1.34. Хоча знаменник стає маленьким поруч$x=1$, чисельник теж стає маленьким, що відповідає кроку знаменника для кроку. По суті, факторинг чисельника, ми отримуємо\[f(x)=\frac{(x-1)(x+1)}{x-1}.\]

Скасувавши загальний термін, ми отримуємо, що$f(x)=x+1$ для$x\not=1$. Таким чином, явно немає асимптоти, скоріше діра існує в графіку в$x=1$.

$альт$
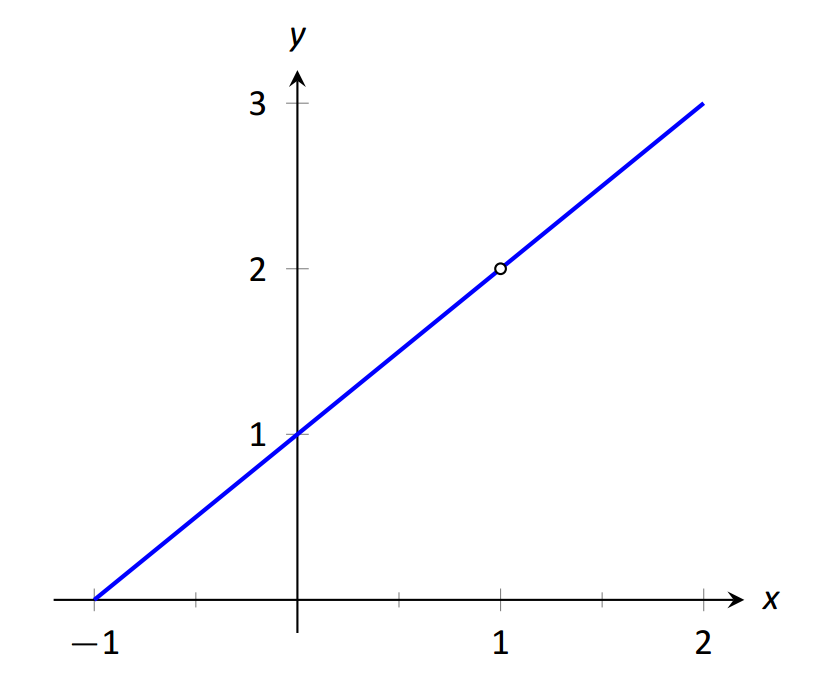
$\text{FIGURE 1.34}$: Графічно показуючи, що$f(x)=\frac{x^2-1}{x-1}$ не має асимптоту в$x=1$.

Наведений вище приклад може здатися трохи надуманим. Ще одним прикладом, що демонструє цю важливу концепцію, є$f(x)= (\sin x)/x$. Цю функцію ми розглядали кілька разів в попередніх розділах. Ми виявили, що$ \lim\limits_{x\to0}\frac{\sin x}{x}=1$; тобто немає вертикальної асимптоти. Жодне просте алгебраїчне скасування не робить цей факт очевидним; ми використали теорему стискання в розділі 1.3, щоб довести це.

Якщо знаменник дорівнює 0 в певній точці, а чисельник - ні, то зазвичай в цій точці буде вертикальна асимптота. З іншого боку, якщо чисельник і знаменник є нулем у цій точці, то в цій точці може бути або не бути вертикальної асимптоти. Цей випадок, коли чисельник і знаменник обидва нуль повертає нас до важливої теми.

невизначені форми

Ми бачили, як межа

\[\lim\limits_{x\rightarrow 0}\frac{\sin x}{x}\quad \text{and}\quad \lim\limits_{x\to1}\frac{x^2-1}{x-1}\]кожен повертає невизначену форму "$0/0$", коли ми сліпо підключаємо$x=0$ і$x=1$, відповідно. Однак не$0/0$ є дійсним арифметичним виразом. Це не вказує на те, що відповідні межі 1 і 2.

З невеликою розумністю можна придумати$0/0$ вирази, які мають межу$\infty$, 0 або будь-яке інше дійсне число. Саме тому цей вислів називають індетермінантним.

Ключова концепція, яку слід зрозуміти, полягає в тому, що такі обмеження насправді не повертаються$0/0$. Швидше, майте на увазі, що ми приймаємо обмеження. Що насправді відбувається, так це те, що чисельник скорочується до 0, тоді як знаменник також скорочується до 0. Відповідні ставки, за якими вони це роблять, дуже важливі і визначають фактичне значення ліміту.

Невизначена форма вказує на те, що потрібно зробити більше роботи, щоб обчислити ліміт. Ця робота може бути алгебраїчною (наприклад, факторинг та скасування) або може вимагати такого інструменту, як теорема стискання. У наступному розділі ми вивчимо техніку під назвою L'hospital Правило, яка забезпечує інший спосіб обробки невизначені форми.

Деякі інші поширені невизначені форми є$\infty-\infty$,$\infty\cdot 0$,$\infty/\infty$,$0^0$,$\infty^0$ і$1^{\infty}$. Знову ж таки, майте на увазі, що це «сліпі» результати оцінки межі, і кожен, сам по собі, не має сенсу. Вираз насправді не$\infty-\infty$ означає «відняти нескінченність з нескінченності». Швидше, це означає «Одна кількість віднімається від іншої, але обидві ростуть без зв'язку». Який результат? Можна отримати кожне значення між$-\infty$ і$\infty$

Зверніть увагу, що$1/0$ і не$\infty/0$ є невизначеними формами, хоча вони також не є абсолютно дійсними математичними виразами. У кожному функція зростає без обмежень, вказуючи на те, що межа буде$\infty$$-\infty$, або просто не існує, якщо ліві і праві межі не збігаються.

Межі на нескінченності та горизонтальні асимптоти

На початку цього розділу ми коротко розглянули, що відбувається з тим$f(x) = 1/x^2$, як$x$ виросли дуже великі. Графічно це стосується поведінки функції до «крайнього правого» графіка. Ми робимо це поняття більш явним у наступному визначенні.

Визначення 6: Межі на нескінченності та горизонтальна асимптота

Ми говоримо,$\lim\limits_{x\rightarrow\infty} f(x)=L$ якщо для кожного$\epsilon>0$ існує$M>0$ таке, що якщо$x\geq M$, то$|f(x)-L|<\epsilon$.
Ми говоримо,$\lim\limits_{x\rightarrow-\infty} f(x)=L$ якщо для кожного$\epsilon>0$ існує$M<0$ таке, що якщо$x\leq M$, то$|f(x)-L|<\epsilon$.
Якщо$\lim\limits_{x\rightarrow\infty} f(x)=L$ або$\lim\limits_{x\rightarrow-\infty} f(x)=L$, ми говоримо, що$y=L$ це горизонтальна асимптота$f$.

Ми також можемо визначити межі, наприклад,$\lim\limits_{x\rightarrow\infty}f(x)=\infty$ об'єднавши це визначення з Визначенням 5.

Приклад 29: Апроксимація горизонтальних асимптотів

Наближена горизонтальна асимптота (и) з$ f(x)=\frac{x^2}{x^2+4}$.

Рішення

Ми наблизимо горизонтальні асимптоти шляхом наближення меж\[\lim\limits_{x\to-\infty} \frac{x^2}{x^2+4}\quad \text{and}\quad \lim\limits_{x\to\infty} \frac{x^2}{x^2+4}.\] Рис. 1.35 (а) показує ескіз$f$, а частина (b) дає значення$f(x)$ для великих величин величини$x$. Здається розумним зробити висновок з обох цих джерел, що$f$ має горизонтальну асимптоту при$y=1$.

$альт$ $альт$
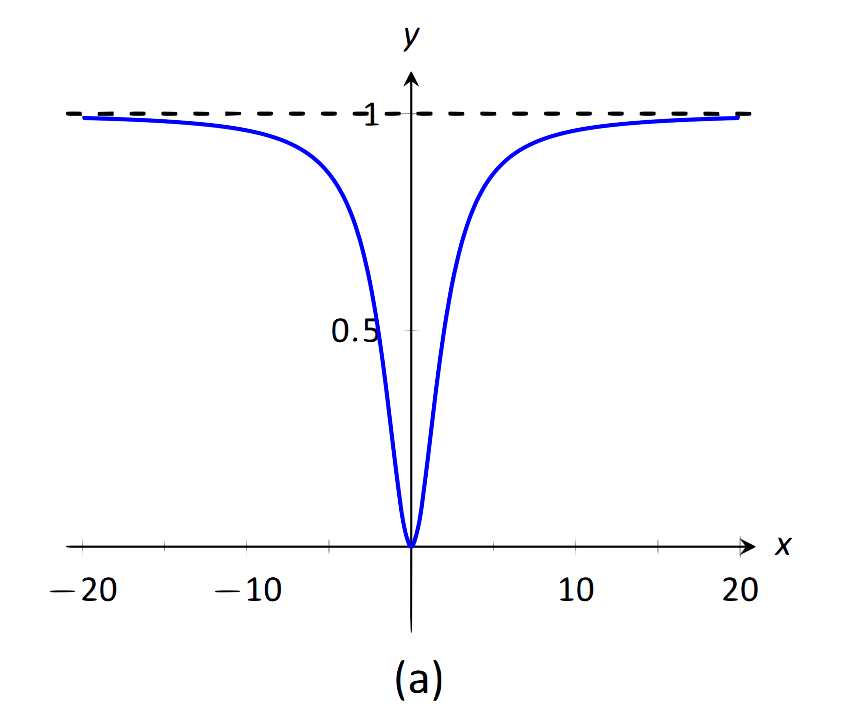
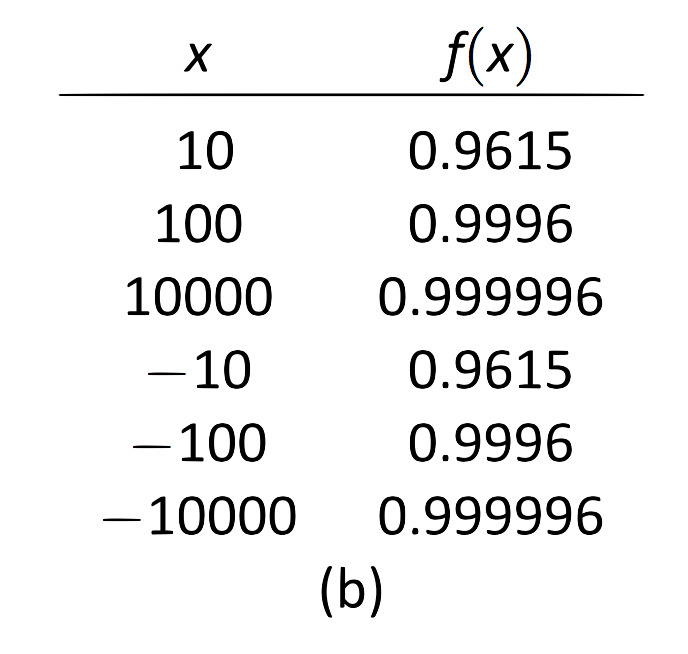
$\text{FIGURE 1.35}$: Використання графіка та таблиці для наближення горизонтальної асимптоти у прикладі 29.

Пізніше ми покажемо, як визначити це аналітично.

Горизонтальні асимптоти можуть приймати найрізноманітніші форми. На малюнку 1.36 (a) показано, що$f(x) = x/(x^2+1)$ має горизонтальну асимптоту$y=0$, де 0 наближається як зверху, так і знизу.

На малюнку 1.36 (b) показано, що$f(x) =x/\sqrt{x^2+1}$ має два горизонтальних асимптоти; один на,$y=1$ а інший в$y=-1$.

Рисунок 1.36 (c) показує, що$f(x) = (\sin x)/x$ має ще більш цікаву поведінку, ніж просто$x=0$; як$x$ наближається$\pm\infty$,$f(x)$ наближається до 0, але коливається, як це робить.

$альт$
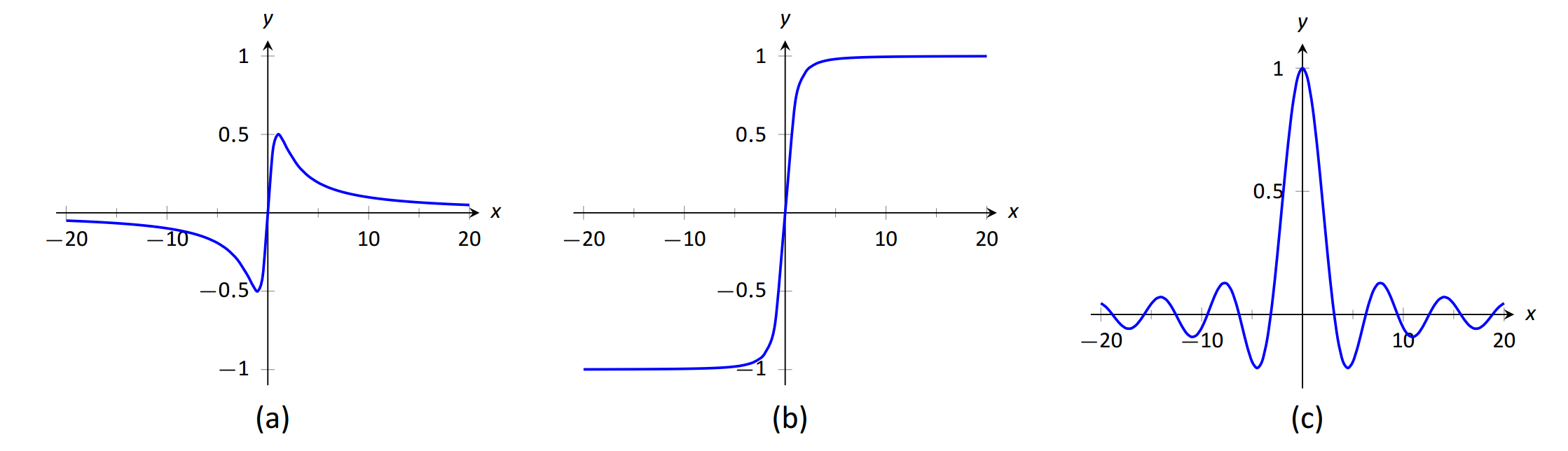
$\text{FIGURE 1.36}$: Враховуючи різні типи горизонтальних асимптотів.

Ми можемо аналітично оцінити межі на нескінченності для раціональних функцій, як тільки зрозуміємо$\lim\limits_{x\rightarrow\infty} 1/x$. Коли$x$ стає все більше і більше, то$1/x$ стає все менше і менше, наближаючись до 0. Ми можемо, насправді, зробити$1/x$ так мало, як ми хочемо, вибравши досить велике значення$x$. З огляду на$\epsilon$, що ми можемо зробити$1/x<\epsilon$, вибираючи$x>1/\epsilon$. Таким чином ми маємо$\lim\limits_{x\rightarrow\infty} 1/x=0$.

Зараз не дуже стрибок, щоб зробити висновок про наступне:

\[\lim\limits_{x\rightarrow\infty}\frac1{x^n}=0\quad \text{and}\quad \lim\limits_{x\rightarrow-\infty}\frac1{x^n}=0\]

Тепер припустимо, нам потрібно обчислити наступну межу:

\[\lim\limits_{x\rightarrow\infty}\frac{x^3+2x+1}{4x^3-2x^2+9}.\]

Хороший спосіб наблизитися до цього - розділити через чисельник і знаменник на$x^3$ (отже, ділення на 1), що є найбільшою$x$ силою з'являтися у функції. Роблячи це, отримуємо

\[\begin{align*}\lim\limits_{x\rightarrow\infty}\frac{x^3+2x+1}{4x^3-2x^2+9} &=\lim\limits_{x\rightarrow\infty}\frac{1/x^3}{1/x^3}\cdot\frac{x^3+2x+1}{4x^3-2x^2+9}\\ &=\lim\limits_{x\rightarrow\infty}\frac{x^3/x^3+2x/x^3+1/x^3}{4x^3/x^3-2x^2/x^3+9/x^3}\\ &= \lim\limits_{x\rightarrow\infty}\frac{1+2/x^2+1/x^3}{4-2/x+9/x^3}.\end{align*}\]

Тоді використовуючи правила для лімітів (які також тримають за межі на нескінченності), а також факт про межі$1/x^n$, ми бачимо, що межа стає\[\frac{1+0+0}{4-0+0}=\frac14.\]

Ця процедура працює для будь-якої раціональної функції. Насправді вона дає нам наступну теорему.

Теорема 11: Межі раціональних функцій на нескінченності

$f(x)$Дозволяти раціональну функцію наступного виду:

\[f(x)=\frac{a_nx^n + a_{n-1}x^{n-1}+\dots + a_1x + a_0}{b_mx^m + b_{m-1}x^{m-1} + \dots + b_1x + b_0},\]

де будь-який з коефіцієнтів може дорівнювати 0, крім$a_n$ і$b_m$.

Якщо$n=m$, то$\lim\limits_{x\rightarrow\infty} f(x) = \lim\limits_{x\rightarrow-\infty} f(x) = \frac{a_n}{b_m}$.
Якщо$n<m$, то$\lim\limits_{x\rightarrow\infty} f(x) = \lim\limits_{x\rightarrow-\infty} f(x) = 0$.
Якщо$n>m$, то$\lim\limits_{x\rightarrow\infty} f(x)$ і$\lim\limits_{x\rightarrow-\infty} f(x)$ обидва нескінченні.

Ми можемо зрозуміти, чому це правда. Якщо найвища сила однакова як у чисельнику, так і в знаменнику (тобто$n=m$), ми опинимося в ситуації, подібній до наведеного вище прикладу, де ми розділимо на$x^n$ і в межі всі члени наближаються до 0, крім$a_nx^n/x^n$ і$b_mx^m/x^n$.$x$ Так як$n=m$, це залишить нас з лімітом$a_n/b_m$. Якщо$n<m$, то після ділення через на$x^m$, всі члени в чисельнику наближаються до 0 в межі, залишивши нас з$0/b_m$ або 0. Якщо$n>m$, і ми намагаємося ділити через на$x^n$, ми в кінцевому підсумку з усіма термінами в знаменнику прагнуть до 0, в той час як$x^n$ термін в чисельнику не наближається до 0. Це свідчить про якусь нескінченну межу.

Інтуїтивно, як$x$ стає дуже великим, всі терміни в чисельнику малі в порівнянні з$a_nx^n$, і аналогічно всі терміни в знаменнику малі в порівнянні з$b_nx^m$. Якщо$n=m$, дивлячись лише на ці два важливі терміни, ми маємо$(a_nx^n)/(b_nx^m)$. Це зводиться до$a_n/b_m$. Якщо$n<m$, функція поводиться як$a_n/(b_mx^{m-n})$, яка прагне до 0. Якщо$n>m$ функція поводиться як$a_nx^{n-m}/b_m$, яка буде, як правило,$\infty$ або$-\infty$ залежно від значень$n$$m$$a_n$,,$b_m$ і чи шукаєте ви$\lim\limits_{x\rightarrow\infty} f(x)$ або$\lim\limits_{x\rightarrow-\infty} f(x)$.

З обережністю ми можемо швидко оцінити межі на нескінченності для великої кількості функцій, враховуючи найбільші повноваження$x$. Наприклад, розглянемо знову$\lim\limits_{x\to\pm\infty}\frac{x}{\sqrt{x^2+1}},$ графічний малюнок\ ref {fig:hzasy} (b). Коли$x$ дуже великий,$x^2+1 \approx x^2$. Таким чином,\[\sqrt{x^2+1}\approx \sqrt{x^2} = |x|,\quad \text{and}\quad \frac{x}{\sqrt{x^2+1}} \approx \frac{x}{|x|}.\] Цей вираз дорівнює 1$x$, коли позитивний, а$-1$ коли$x$ негативний. Звідси ми отримуємо асимптоти$y=1$ і$y=-1$, відповідно.

Приклад 30: Пошук межі раціональної функції

Аналітично підтвердіть, що$y=1$ це горизонтальна асимптота$ f(x) = \frac{x^2}{x^2+4}$, як наближено у прикладі 29.

Рішення

Перш ніж використовувати теорему 11, скористаємося методикою оцінки меж на нескінченності раціональних функцій, що призвело до цієї теореми. Найбільша сила$x$ in$f$ дорівнює 2, тому розділіть чисельник і знаменник$f$ на$x^2$, потім візьміть межі.

\[\begin{align*}\lim\limits_{x\to\infty}\frac{x^2}{x^2+4} &= \lim\limits_{x\to\infty}\frac{x^2/x^2}{x^2/x^2+4/x^2}\\ &=\lim\limits_{x\to\infty}\frac{1}{1+4/x^2}\\ &=\frac{1}{1+0}\\ &= 1. \end{align*}\]

Ми також можемо використовувати теорему 11 безпосередньо; в цьому випадку$n=m$ таким чином межа - це відношення провідних коефіцієнтів чисельника і знаменника, тобто 1/1 = 1.

Приклад 31: Пошук меж раціональних функцій

Використовуйте теорему 11 для оцінки кожного з наступних меж.

$\begin{align}&1.\,\,\lim\limits_{x\rightarrow-\infty}\frac{x^2+2x-1}{x^3+1} \qquad\qquad &&3.\,\,\lim\limits_{x\rightarrow\infty}\frac{x^2-1}{3-x} \\ &2.\,\,\lim\limits_{x\rightarrow\infty}\frac{x^2+2x-1}{1-x-3x^2} && \\ \end{align}$

$альт$ $альт$ $альт$
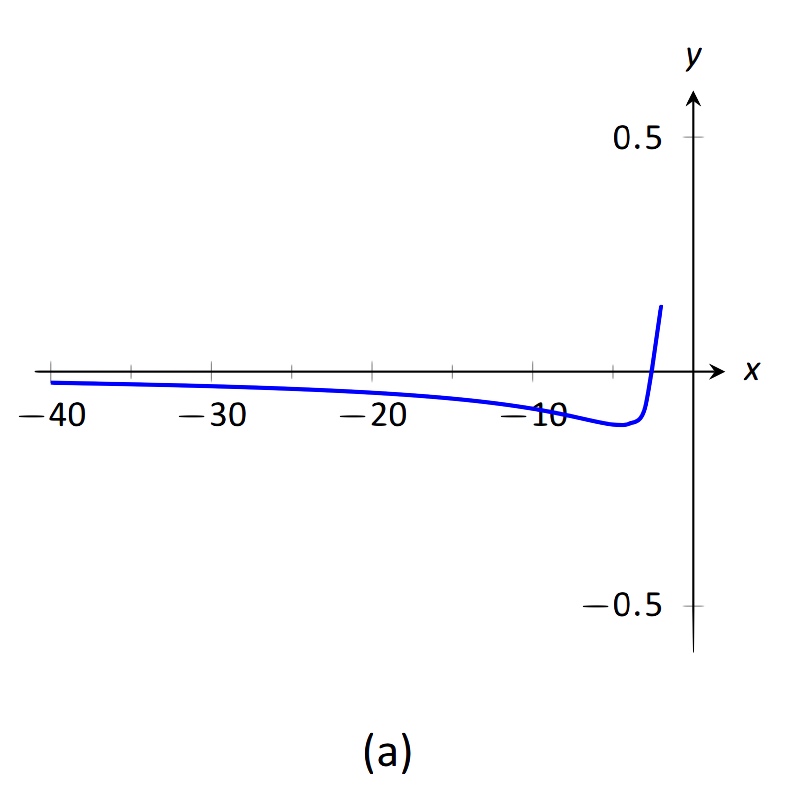
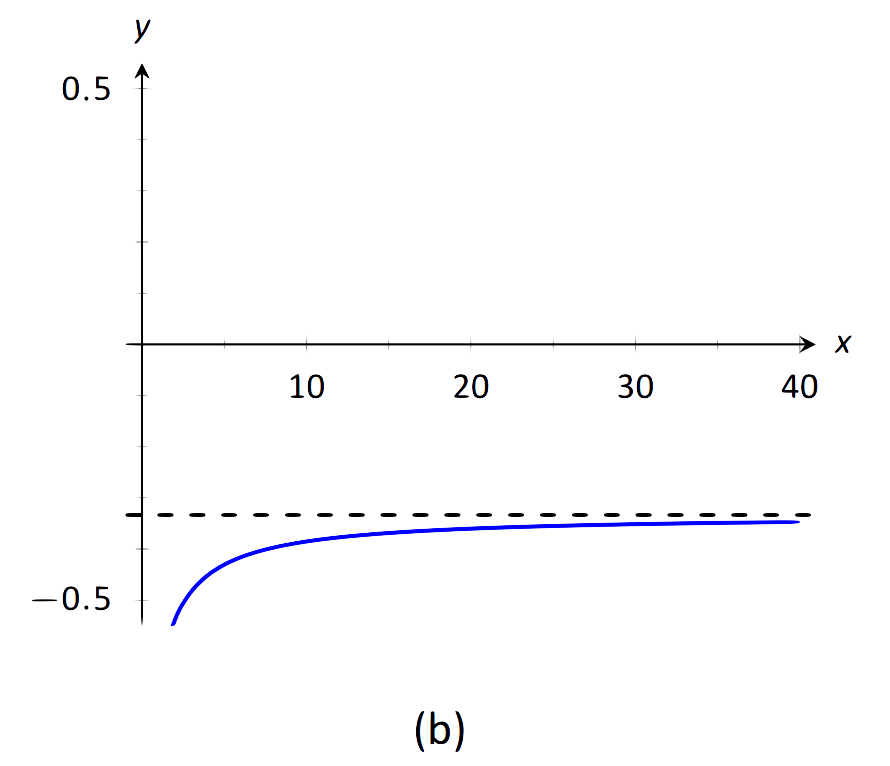
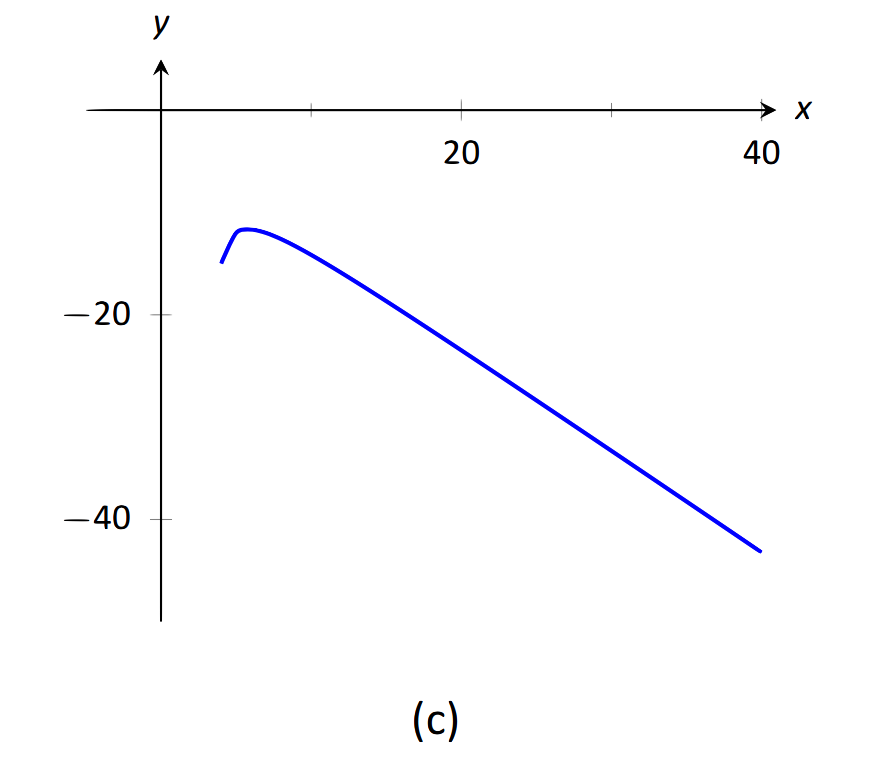
$\text{FIGURE 1.37}$: Візуалізація функцій у прикладі 31.

Рішення

Найвища сила$x$ знаходиться в знаменнику. Тому межа дорівнює 0; див. Рис. 1.37 (а).
Найвища сила$x$ є$x^2$, яка зустрічається як в чисельнику, так і в знаменнику. Таким чином, межа - це відношення коефіцієнтів$x^2$, який є$-1/3$. Див. Малюнок 1.37 (б).
Найвища сила$x$ знаходиться в чисельнику, тому межа буде$\infty$ або$-\infty$. Щоб побачити які, розглянемо тільки домінуючі члени з чисельника і знаменника, які є$x^2$ і$-x$. Вираз в межі буде вести себе як$x^2/(-x) = -x$ для великих значень$x$. Тому межа є$-\infty$. Див. Малюнок 1.37 (с).

Резюме глави

У цьому розділі ми:

визначив ліміт,
знайшли доступні способи наближення їх значень чисельно і графічно,
розробив не дуже простий метод доведення значення межі ($\epsilon-\delta$доказів),
досліджували, коли меж не існує,
визначено неперервність і досліджені властивості неперервних функцій, і
вважаються межі, які беруть участь нескінченність.

Чому? Математика славиться побудовою на собі і обчислення виявляється не винятком. У наступному розділі нас буде цікавити «ділення на 0». Тобто ми захочемо розділити величину на меншу і меншу кількість і подивитися, до якого значення наближається частка. Іншими словами, ми захочемо знайти межу. Ці обмеження дозволять нам, серед іншого, визначити, наскільки швидко щось рухається, коли нам надається лише інформація про позицію.

Пізніше ми захочемо скласти нескінченний список чисел. Ми зробимо це, спочатку склавши кінцевий список чисел, а потім візьміть обмеження, оскільки кількість речей, які ми додаємо, наближається до нескінченності. Дивно, але ця сума часто є кінцевою; тобто ми можемо скласти нескінченний список чисел і отримати, наприклад, 42.

Це лише два короткі приклади того, чому ми зацікавлені в лімітах. Багатьом студентам не подобається ця тема, коли вони вперше знайомляться з нею, але з часом часто формується оцінка на основі сфери її застосування.

Автори та авторства

Template:ContribApexCalc