1.30: Стандартне відхилення

Last updated
Save as PDF

Page ID: 65854

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ця тема вимагає стрибка віри. Це один з рідкісних випадків, коли цей підручник скаже: «Не турбуйтеся про те, чому це правда; просто прийміть це».

Нормальний розподіл, який часто називають кривою дзвінка, симетричний зліва та справа, причому середнє, медіана та режим є значенням у центрі. Є багато значень даних поблизу центру, потім все менше і менше, оскільки значення потрапляють далі від центру. Нормальний розподіл описує дані в багатьох реальних ситуаціях: висоти людей, ваги людей, помилки в вимірюванні, бали на стандартизованих тестах (IQ, SAT, ACT)...

Одним з найкращих способів продемонструвати нормальний розподіл є падіння кульок через дошку рівномірно розташованих кілочків, як показано тут. ^[1] Кожен раз, коли м'яч потрапляє в кілочок, він має п'ятдесят п'ятдесят шансів піти вліво або вправо. Для більшості куль кількість лівих і прав приблизно рівні, а м'яч приземляється поблизу центру. Лише кілька куль мають надзвичайно однобоке число лівих і прав, тому на обох кінцях не так багато куль. Як бачите, розподіл не є ідеальним, але він наближений нормальною кривою, намальованою на склі.

$демонстрація наукового музею, показуючи кульки впали, утворюючи криву$

Стандартне відхилення є мірою розкиду даних: дані з великою кількістю чисел, близьких до середнього, мають менше стандартне відхилення, а дані з числами, віддаленими далі від середнього, мають більше стандартне відхилення. (У цьому підручнику вам буде дано значення стандартного відхилення даних і ніколи не потрібно буде його обчислювати.) Стандартне відхилення - це вимірювальна паличка для певного набору даних.

У нормальному розподілі...

приблизно$68\%$ з чисел знаходяться в межах$1$ стандартного відхилення вище або нижче середнього
приблизно$95\%$ з чисел знаходяться в межах$2$ стандартних відхилень вище або нижче середнього
приблизно$99.7\%$ з чисел знаходяться в межах$3$ стандартних відхилень вище або нижче середнього

Це правило 68-95-99.7 називається емпіричним правилом, оскільки воно засноване на спостереженні, а не на деякій формулі. Ніхто не виявив розрахунку, щоб з'ясувати цифри$68\%$$95\%$, і$99.7\%$ до факту. Замість цього, статистики розглянули безліч різних прикладів нормально розподілених даних і сказали: «Mon Dieu, здається, що якщо підрахувати значення даних, які знаходяться в межах одного стандартного відхилення вище або нижче середнього, ви маєте про$68\%$ дані!» і так далі. ^[2]

Наступне зображення шведською мовою, але ви, ймовірно, можете розшифрувати його, оскільки математика є міжнародною мовою.

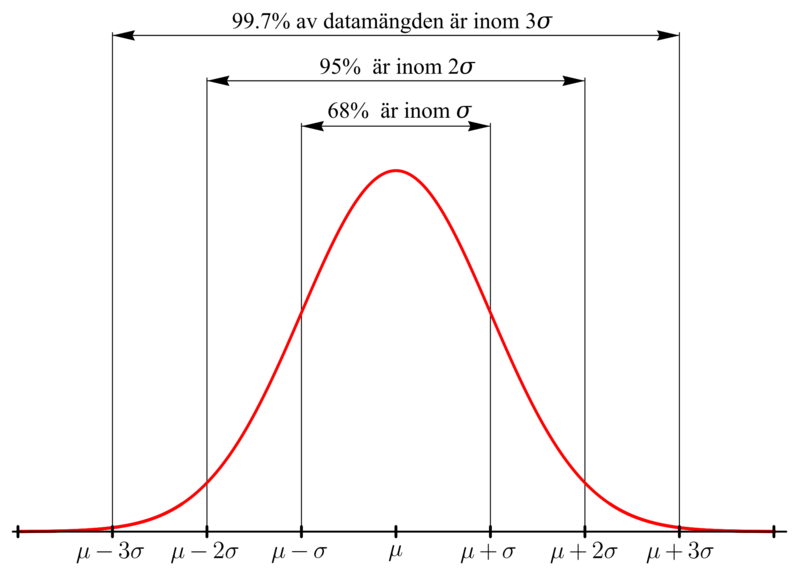
$крива дзвінка, що показує правило 68-95-99.7: відповідні вертикальні лінії на одну одиницю ліворуч і праворуч від центру включають 68 відсотків даних, відповідні вертикальні лінії дві одиниці ліворуч і праворуч від центру включають 95 відсотків даних, і відповідні вертикальні лінії три одиниці ліворуч і праворуч від центру центр включає 99,7 відсотка даних.$

Давайте повернемося до експерименту, що скидає кульку, і давайте припустимо, що стандартне відхилення становить три стовпці шириною. ^[3] На малюнку нижче зелена лінія позначає центр розподілу.

$демонстрація наукового музею, що показує кулі, що впали, утворюючи криву дзвоника, з вертикальними лініями, намальованими, щоб показати$

По-перше, дві червоні лінії - це кожні три стовпці від центру, що є одним стандартним відхиленням вище і нижче центру, тому близько 68% куль буде приземлятися між червоними лініями.

Далі дві помаранчеві лінії - це ще три стовпці далі від центру, що становить шість стовпців або два стандартних відхилення вище і нижче центру, тому близько 95% куль буде приземлятися між помаранчеві лінії.

І, нарешті, дві фіолетові лінії - це ще три стовпці далі від центру, що становить дев'ять стовпців або три стандартні відхилення вище і нижче центру, так що близько 99,7% куль буде приземлитися між фіолетовими лініями. Можна$997$ очікувати, що з$1,000$ кульок приземляться між фіолетовими лініями, залишаючи тільки$3$ поза$1,000$ посадкою за фіолетовими лініями з обох кінців.

Ось результати гри Даміана Лілларда за набрані очки, в порядку зростання, за$80$ ігри, які він грав у сезоні НБА 2018-19. ^[4] Це розбито на вісім рядків по десять чисел кожен, і це загальна кількість$2,069$ очок.

$11$,$13$,$13$,,$13$,$14$,$14$,$15$,$15$,$15$,$16$,,
$16$,$16$,$17$,$17$,$17$,$18$,$18$,,$19$,$19$,$20$,
$20$,$20$,$20$,,$20$,$21$,$21$,$22$,$22$,$23$,$23$,,
$23$,$23$,$24$,$24$,$24$,$24$,$24$,,$24$,$24$,$24$,
$25$,$25$,$25$,,$26$,$26$,$26$,$28$,$28$,$28$,$29$,,
$29$,$29$,$29$,$30$,$30$,$30$,$30$,,$30$,$31$,$31$,
$33$,$33$,$33$,,$33$,$33$,$33$,$34$,$34$,$34$,$35$,,
$36$,$36$,$37$,$39$,$40$,$40$,,$41$,$41$,$42$,$51$

Вправи$\PageIndex{1}$

Це огляд середнього, медіани та режиму; вам потрібно знати середнє значення, щоб виконати наступні вправи стандартного відхилення.

1. Що таке середнє значення даних? (Округлити до найближчої десятої.)

2. Яка медіана даних?

3. Який режим даних?

4. Чи будь-який середній, медіанний або режим здається оманливим, або всі три, здається, представляють дані досить добре?

Відповідь

1. $25.9$балів

2. $24.5$балів

3. $24$балів (що відбувалося вісім разів)

4. всі три, здається, представляють типову кількість набраних балів; середнє значення трохи високе, оскільки немає надзвичайно низьких значень, але є кілька високих значень, які тягнуть середнє значення вгору.

Ось гістограма даних, довільно згрупована в сім однаково розташованих інтервалів. Це показує, що дані приблизно слідують за дзвоноподібною кривою, дещо усіченою зліва та з викидом праворуч.

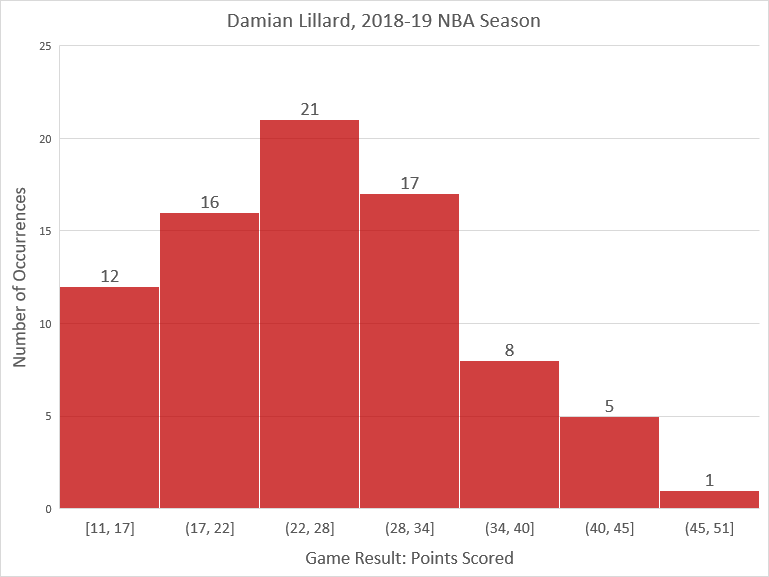
$гістограма або гістограма, що показує 12 балів між 11 і 17, 16 балів вище 17 і до 22, 21 балів вище 22 і до 28, 17 балів вище 28 і до 34, 8 балів вище 34 і до 40, 5 балів вище 40 і до 45, і 1 оцінка вище 45 і до 51.$

Якщо ми введемо дані в програму електронних таблиць, таку як Microsoft Excel або Google Таблиці, ми можемо швидко виявити, що стандартне відхилення - це$8.2$ точки.

Виходячи з емпіричного правила, слід очікувати, що приблизно$68\%$ результати будуть знаходитися в межах$8.2$ пунктів вище і нижче середнього.

Вправи$\PageIndex{1}$

5. Визначте діапазон набраних балів, які знаходяться в межах одного стандартного відхилення від середнього.

6. Скільки результатів$80$ гри знаходяться в межах одного стандартного відхилення від середнього?

7. Чи близька попередня відповідь до$68\%$ загальної кількості результатів гри?

Відповідь

5. $17.7$до$34.1$ очок

6. $54$результатів$80$ гри

7. так;$54\div80=67.5\%$

І ми повинні очікувати, що приблизно$95\%$ результати будуть в межах$2\cdot8.2=16.4$ пунктів вище і нижче середнього.

Вправи$\PageIndex{1}$

8. Визначте діапазон набраних балів, які знаходяться в межах двох стандартних відхилень від середнього.

9. Скільки результатів$80$ гри знаходяться в межах двох стандартних відхилень від середнього?

10. Чи близька попередня відповідь до$95\%$ загальної кількості результатів гри?

Відповідь

8. $9.5$до$42.3$ очок

9. $79$результатів$80$ гри

10. начебто близько, але не дуже;$79\div80=98.75\%$

І ми повинні очікувати, що приблизно$99.7\%$ результати будуть в межах$3\cdot8.2=24.6$ пунктів вище і нижче середнього.

Вправи$\PageIndex{1}$

11. Визначте діапазон набраних балів, які знаходяться в межах трьох стандартних відхилень від середнього.

12. Скільки результатів$80$ гри знаходяться в межах трьох стандартних відхилень від середнього?

13. Чи близька попередня відповідь до$99.7\%$ загальної кількості результатів гри?

Відповідь

11. $1.3$до$50.5$ очок

12. $79$результатів$80$ гри, знову

13. так, це досить близько;$79\div80=98.75\%$

Зверніть увагу, що ми могли б думати про стандартні відхилення, як похибка вимірювання або толерантність: середнє$\pm8.2$, середнє значення$\pm16.4$, середнє значення$\pm24.6$...

Вправи$\PageIndex{1}$

Для американських жінок середня висота становить близько$63.5$ дюймів ($5$футів$3.5$), а стандартне відхилення -$3$ дюйми. Використовуйте емпіричне правило, щоб заповнити пробіли.

14. $68\%$Приблизно жінки повинні бути від _______ до _______ дюймів зросту.

15. $95\%$Приблизно жінки повинні бути від _______ до _______ дюймів зросту.

16. $99.7\%$Приблизно жінки повинні бути від _______ до _______ дюймів зросту.

Для чоловіків США середня висота становить близько$69.5$ дюймів ($5$футів$9.5$), а стандартне відхилення -$3$ дюйми. Використовуйте емпіричне правило, щоб заповнити пробіли.

17. Близько$68\%$ чоловіків має бути від _______ до _______ дюймів у висоту.

18. Близько$95\%$ чоловіків має бути від _______ до _______ дюймів у висоту.

19. Близько$99.7\%$ чоловіків має бути від _______ до _______ дюймів у висоту.

Відповідь

14. $60.5$;$66.5$

15. $57.5$;$69.5$

16. $54.5$;$72.5$

17. $66.5$;$72.5$

18. $63.5$;$75.5$

19. $60.5$;$78.5$

Цей графік на https://tall.life/height-percentile-calculator-age-country/ показує, що, оскільки стандартні відхилення рівні, дві криві дзвінка мають по суті однакову форму, але жіночий графік зосереджений на шість дюймів нижче чоловічого.

Вправи$\PageIndex{1}$

Близько$16\%$ американських самців у сорокові роки важать менше$160$ фунтів і$16\%$ важать більше$230$ фунтів ^[5] Припустіть нормальний розподіл.

20. Який відсоток американських чоловіків важать від$160$ lb і$230$ lb?

21. Яка середня вага? (Підказка: подумайте про симетрію.)

22. Що таке стандартне відхилення? (Підказка: Ви повинні працювати назад, щоб зрозуміти це, але математика не складна.)

23. Виходячи з емпіричного правила, близько$95\%$ чоловіків повинні важити від _______ до _______ фунтів.

Відповідь

20. $68\%$тому що$100\%-(16\%+16\%)=68\%$

21. $195$lb тому що це на півдорозі між$160$ і$230$ lb

22. $35$$195-35$lb тому що$195+35$ lb і lb охоплює$68\%$ дані

23. $125$;$265$

Якщо вам задають тільки одне питання про емпіричному правилі замість трьох в ряд ($68\%$,,$99.7\%$)$95\%$, вас, швидше за все, запитають про$95\%$. Це пов'язано з «$95\%$довірчим інтервалом», який часто згадується стосовно статистики. Наприклад, похибка для опитування зазвичай близька до двох стандартних відхилень. ^[6]

Давайте закінчимо, порівнявши показники трьох команд НФЛ з рубежу століть.

Кількість ігор регулярного сезону, які виграли «Нова Англія Патріоти» кожного сезону НФЛ від 2001-19: ^[7]

рік	виграє
2001	$11$
2002	$9$
2003	$14$
2004	$14$
2005	$10$
2006	$12$
2007	$16$
2008	$11$
2009	$10$
2010	$14$
2011	$13$
2012	$12$
2013	$12$
2014	$12$
2015	$12$
2016	$14$
2017	$13$
2018	$11$
2019	$12$

Вправи$\PageIndex{1}$

Для Патріотів середня кількість виграшів становить$12.2$, і електронна таблиця говорить нам, що стандартне відхилення - це$1.7$ виграші.

24. Існує$95\%$ ймовірність того, що Патріоти виграють між _______ та _______ іграми в сезоні.

25. У 2020 році «Патріоти» виграли$7$ ігри. Чи могли б ви передбачити це на основі даних? Скільки стандартних відхилень від середнього становить це число виграшів?

Відповідь

24. $8.8$;$15.6$

25. Ви б не передбачили цього з даних, оскільки це більше двох стандартних відхилень нижче середнього, тому буде приблизно$2.5\%$ ймовірність того, що це станеться випадковим чином. Насправді трохи більше,$(12.2-7)\div1.7$ ніж$3$, тому це більше трьох стандартних відхилень нижче середнього, що робить його ще більш малоймовірним. (Можливо, ви передбачили, що патріоти погіршаться, коли Том Брейді залишив їх у Тампа-Бей, але ви б не передбачили лише$7$ перемоги на основі попередніх дев'ятнадцяти років даних.)

Кількість ігор регулярного сезону, виграних Баффало Біллс кожного сезону НФЛ від 2001-19: ^[8]

рік	виграє
2001	$3$
2002	$8$
2003	$6$
2004	$9$
2005	$5$
2006	$7$
2007	$7$
2008	$7$
2009	$6$
2010	$4$
2011	$6$
2012	$6$
2013	$6$
2014	$9$
2015	$8$
2016	$7$
2017	$9$
2018	$6$
2019	$10$

Вправи$\PageIndex{1}$

Для законопроектів середня кількість виграшів є$6.8$, і електронна таблиця говорить нам, що стандартне відхилення - це$1.7$ виграші.

26. Існує$95\%$ ймовірність того, що законопроекти виграють між _______ та _______ іграми в сезоні.

27. У 2020 році законопроекти виграли$13$ ігри. Чи могли б ви передбачити це на основі даних? Скільки стандартних відхилень від середнього становить це число виграшів?

Відповідь

26. $3.4$;$10.2$

27. Ви б не прогнозували це з даних, оскільки це більше двох стандартних відхилень вище середнього, тому буде приблизно$2.5\%$ ймовірність того, що це станеться випадковим чином. Насправді$(13-6.8)\div1.7\approx3.6$, так це більше трьох стандартних відхилень вище середнього, що робить його ще більш малоймовірним. Цей збільшений загальний виграш частково пояснюється зовнішніми силами (тобто, Патріоти стають слабшими і програють дві гри законопроектів), але навіть$11$ перемоги були б сміливим прогнозом, не кажучи вже про$13$.

Кількість ігор регулярного сезону, виграних Денвер Бронкос кожного сезону НФЛ з 2001-19: ^[9]

рік	виграє
2001	$8$
2002	$9$
2003	$10$
2004	$10$
2005	$13$
2006	$9$
2007	$7$
2008	$8$
2009	$8$
2010	$4$
2011	$8$
2012	$13$
2013	$13$
2014	$12$
2015	$12$
2016	$9$
2017	$5$
2018	$6$
2019	$7$

Вправи$\PageIndex{1}$

Для Бронкос середня кількість виграшів становить$9.1$, і електронна таблиця говорить нам, що стандартне відхилення - це$2.6$ виграші.

28. Існує$95\%$ ймовірність того, що Бронкос виграє між _______ та _______ іграми в сезоні.

29. У 2020 році «Бронкос» виграв$5$ ігри. Чи могли б ви передбачити це на основі даних? Скільки стандартних відхилень від середнього становить це число виграшів?

Відповідь

28. $3.9$;$14.3$

29. Проблема з прогнозами про Бронкос полягає в тому, що їх стандартне відхилення настільки велике. Ви можете вибрати будь-яке число між$4$ і$14$ виграє і бути в$95\%$ інтервалі. $(9.1-5)\div2.6\approx1.6$, Так що це близько$1.6$ стандартних відхилень нижче середнього, що робить його не дуже незвичайним. У той час як Патріоти і законопроекти більш послідовні, підсумки виграшу Бронкос коливаються досить небагато і тому є більш непередбачуваними.

Гра Плінко на Ціна є найвідомішим прикладом цього; ось кліп Snoop Dogg, який допомагає учаснику виграти гроші. ←
Сповідь: Цей абзац дає вам загальне уявлення про те, як розвивалися ці ідеї, але можуть бути не зовсім історично точними. ←
Я око це, і це здавалося розумним припущенням. ←
Джерело: [1]https://www.basketball-reference.com/players/l/lillada01/gamelog/2019
Джерело: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=17&ved=2ahUKEwjm-d-whavhAhWCFXwKHQxMDz4QFjAQegQIARAC&url=https%3A%2F%2Fwww2.census.gov%2Flibrary%2Fpublications%2F2010%2Fcompendia%2Fstatab%2F130ed%2Ftables%2F11s0205.pdf&usg=AOvVaw1DFDbil78g-qXbIgK6 Ірв
Джерело: [2]https://en.Wikipedia.org/wiki/Standard_deviation
Джерело: [3]https://www.pro-football-reference.com/teams/nwe/index.htm
Джерело: [4]https://www.pro-football-reference.com/teams/buf/index.htm
Джерело: [5]https://www.pro-football-reference.com/teams/den/index.htm

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)

Вправи\(\PageIndex{1}\)