Skip to main content
LibreTexts - Ukrayinska

1.6: Точність та GPE

  1. Last updated
  2. Save as PDF
  • Page ID
    65808

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Точність

    Точність числа - це місце значення правої найзначнішої цифри. Наприклад,\(100.45\) точно на соті місця, а\(3,840\) точні до десятків.

    Вправи\(\PageIndex{1}\)

    Визначте точність (тобто значення місця найправішої значущої цифри) кожного числа.

    1. \(63,400\)

    2. \(63,040\)

    3. \(63,004\)

    4. \(8,000\)

    5. \(8,\overline{0}00\)

    6. \(8,0\overline{0}0\)

    7. \(8,00\overline{0}\)

    8. \(0.085\)

    9. \(0.0805\)

    10. \(0.08050\)

    Відповідь

    1. сотні

    2. десятки

    3. ті

    4. тисячі

    5. сотні

    6. Десятки

    7. ті

    8. Тисячні

    9. Десятисячні

    10. сотень тисячних

    Точність на основі округлення

    У попередньому модулі про десяткові числа ми використовували округлення на основі точності, оскільки ми були округлення до вказаного значення місця; наприклад, округлення до найближчої десятої. Давайте практикуємо це за допомогою овербарів та кінцевих нулів.

    Точне округлення на основі:

    1. Знайдіть округлення цифру в тому місці, до якого ви здійснюєте округлення.
    2. Подивіться на тестову цифру прямо праворуч від округлення цифри.
    3. Якщо контрольна цифра дорівнює 5 або більше, збільште цифру округлення на 1 і опустіть всі цифри праворуч від неї. Якщо контрольна цифра менше 5, залиште округлення однаковою і опустіть всі цифри праворуч від неї.

    Пам'ятайте, коли цифра округлення цілого числа є a\(9\), яка округляється до a\(0\), ми повинні написати перекриття над цим\(0\).

    Крім того, коли цифра округлення десяткового числа є a\(9\), яка округляється до a\(0\), ми повинні включити\(0\) в цей десятковий розряд.

    Вправи\(\PageIndex{1}\)

    Округляйте кожне число до зазначеного значення місця. Обов'язково включіть кінцеві нулі або перекриття, якщо це необхідно.

    11. \(13,997\)(тисячі)

    12. \(13,997\)(сотні)

    13. \(13,997\)(десятки)

    14. \(0.5996\)(десятих)

    15. \(0.5996\)(соті)

    16. \(0.5996\)(тисячні)

    Відповідь

    11. \(14,000\)

    12. \(14,\overline{0}00\)

    13. \(14,0\overline{0}0\)

    14. \(0.6\)

    15. \(0.60\)

    16. \(0.600\)

    Точність при додаванні та відніманні

    Припустимо, відвідуваність великого заходу оцінюється у\(25,000\) людей, але тоді ви бачите, як\(3\) люди йдуть. Це нова оцінка\(24,997\)? Ні, тому що первісна оцінка була точною лише до найближчої тисячі. Ми не можемо почати з неточного числа і закінчити з більш точним числом. Якби ми оцінили, що\(1,000\) люди пішли, то ми могли б переглянути нашу оцінку відвідуваності,\(24,000\) оскільки ця оцінка підтримує той самий рівень точності, що і наша початкова оцінка.

    При додаванні або відніманні чисел з різним рівнем точності відповідь повинна бути округлена до тієї ж точності, що і найменш точні з вихідних чисел.

    Не округляйте початкові числа; спочатку зробіть необхідні обчислення, а потім округліть відповідь як останній крок.

    Вправи\(\PageIndex{1}\)

    Додайте або відніміть, як зазначено. Округлити до відповідного рівня точності.

    17. Знайдіть комбіновану вагу чотирьох упаковок з наступними вагами:\(9.7\) lb,\(13\) lb,\(10.5\) lb,\(6.1\) lb.

    18. Знайдіть комбіновану вагу чотирьох упаковок з наступними вагами:\(9.7\) lb,\(13.0\) lb,\(10.5\) lb,\(6.1\) lb.

    19. Купуючи страховку орендаря, Чандра оцінює вартість свого страхового майна в $\(10,200\). Після продажу деяких предметів, що оцінюються в $\(375\), якою буде переглянута оцінка?

    20. Чандра знає, що вона має приблизно $ на\(840\) своєму чековому рахунку. Після використання своєї дебетової картки для здійснення двох покупок на\(25.95\) суму $ та $\(16.38\), скільки вона залишила б на своєму рахунку?

    Відповідь

    17. \(39\)фунт

    18. \(39.3\)фунт

    19. $\(9,800\)

    20. $\(8\overline{0}0\)

    Якщо ви множаєте на точне число, ви можете вважати це повторним доповненням. Наприклад, припустимо, що ви вимірюєте вагу об'єкта, щоб бути\(4.37\) унціями, і ви хочете знати вагу трьох з цих об'єктів; множення\(4.37\) разів\(3\) таке ж, як додавання\(4.37 + 4.37 + 4.37 = 13.11\) унцій. Точність все ще до сотих місць. Питання про значні цифри не стосується точних цифр, тому було б неправильно розглядати\(3\) як наявність лише одного sig рис. (Ставтеся до точних чисел, як роялті; їх точність ідеальна, і було б образа навіть поставити під сумнів.)

    Найбільша можлива похибка вимірювання (GPE)

    Припустимо, ви зважуєте собаку шкалою, яка відображає вагу, округлену до найближчого фунта. Якщо шкала говорить, що сер Баркс-А-Лот важить\(23\) фунти, він може важити в будь-якому місці від\(22.5\) фунтів до майже\(23.5\) фунтів. Справжня вага може бути стільки, скільки\(0.5\) фунтів вище або нижче виміряної ваги, яку ми могли б написати як\(23\pm0.5\).

    Тепер припустимо, що ви зважуєте сера Баркса-А-Лот за допомогою шкали, яка відображає вагу, округлену до найближчої десятої частини фунта. Якщо шкала говорить, що сер Баркс-А-Лот важить\(23.0\) фунти, ми тепер знаємо, що він може важити в будь-якому місці від\(22.95\) фунтів до майже\(23.05\) фунтів. Справжня вага може бути стільки, скільки\(0.05\) фунтів вище або нижче виміряної ваги, яку ми могли б написати як\(23.0\pm0.05\).

    Зростаючи рівень точності вимірювання, ми зменшуємо найбільшу можливу похибку вимірювання або GPE. GPE завжди половина точності; якщо точність до найближчої десятої\(0.1\), GPE становить половину однієї десятої, або п'яти сотих,\(0.05\). GPE завжди буде a\(5\) в місці праворуч від місця значення точності числа.

    Інший спосіб думати про GPE полягає в тому, що він дає діапазон значень, які округляються до числа, про який йде мова. Повернутися до зважування сера Баркса-А-Лот:\(23\pm0.5\) говорить нам нижнє значення та верхнє значення. \(23-0.5=22.5\)це найнижча вага, який буде округлити до\(23\). Аналогічно,\(23+0.5=23.5\) це найбільша вага, який буде округлити вниз до\(23\). Так, можливо, ми повинні сказати\(23.49\) або\(23.499\), і т.д., для верхньої межі тут, але простіше просто сказати\(23.5\) і погодитися, що\(23.5\) це верхня межа, хоча вона буде округлити вгору, а не вниз. Використовуючи нерівності, ми могли б представити\(23\pm0.5\) як діапазон значень\(22.5\leq\text{weight}<23.5\) замість цього.

    Коли вас попросять ідентифікувати GPE, це може допомогти подумати: «Які мінімальні та максимальні числа, які округляють до заданого числа?» Наприклад, припустимо, що відвідуваність матчу Портленд Торнс оцінюється як\(14,000\) люди. Це число точно до найближчої тисячі. Мінімальне число, яке буде округлити до\(14,000\) буде\(13,500\) (тому що\(13,449\) буде округлити вниз до\(13,000\)), а максимальне число, яке буде округлити вниз,\(14,000\) буде трохи нижче\(14,500\) (тому що\(14,500\) буде округлити до\(15,000\)). Оскільки ці цифри знаходяться\(500\) далеко від\(14,000\), GPE є\(500\). Якщо оцінка вірна до найближчої тисячі, ми знаємо, що фактична відвідуваність знаходиться в межах\(\pm\) 500 від\(14,000\).\(14,000\)

    Вправи\(\PageIndex{1}\)

    21. Пакет важить\(3.76\) кілограми. Що таке ГПЕ?

    22. Рулон пластикового покриття товщиною\(0.00031\) дюймів. Що таке GPE в дюймах?

    23. Пластикові листи товщиною\(0.00031\) дюймів називають\(0.31\) мил. Що таке ГПЕ в милах?

    Відповідь

    21. \(\pm 0.005\)фунт

    22. \(\pm 0.000005\)в

    23. \(\pm 0.005\)мил

    Нагадаємо з попереднього модуля, що точність вимірювання - це кількість значущих цифр. Давайте об'єднаємо ідеї точності, точності та найбільшої можливої похибки вимірювання.

    Вправи\(\PageIndex{1}\)

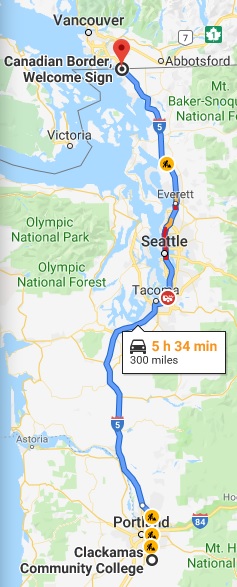
    Карта Google показує 300-мильний маршрут від Громадського коледжу Клакамас на північ до канадського кордону

    Карти Google зазначають, що відстань їзди від головного кампуса CCC до канадського кордону становить\(300\) милі. (Примітка: це округлено до найближчої милі.)

    24. Яка точність?

    25. Що таке точність?

    26. Що таке ГПЕ?

    Очікується, що новий стадіон матиме навколо\(23,000\) місць.

    27. Яка точність?

    28. Що таке точність?

    29. Що таке ГПЕ?

    Ємність бензобака автомобіля -\(14.2\) галони.

    30. Яка точність?

    31. Що таке точність?

    32. Що таке ГПЕ?

    Відповідь

    24. три значущі цифри

    25. одне місце; найближча\(1\) миля

    26. \(\pm 0.5\)милі

    27. дві значущі цифри

    28. тисячі місць; найближчі\(1,000\) місця

    29. \(\pm 500\)сидіння

    30. три значущі цифри

    31. Десяте місце; найближчий\(0.1\) галон

    32. \(\pm 0.05\)галь

    Ось короткий виклад важливих термінів з цих двох модулів. Їх легко змішати, але пам'ятаючи, що «точність» та «значення місця» обидва починаються з «p» може бути корисним.

    Резюме термінів

    Значущі цифри: цифри в числі, які ми довіряємо, щоб бути правильними

    Точність: кількість значущих цифр

    Точність: значення місця найправішої значущої цифри

    Найбільша можлива похибка вимірювання (GPE): половина точності