9.4: Десяткові
- Page ID
- 67017
Значення десяткових знаків найкраще зрозуміти, коли людина має реальне розуміння значення місця та дробів. Десяткове позначення, яке ми зазвичай використовуємо, є продовженням значення місця в десятці основи. Десяткова крапка вказує на те, що наступні цифри представляють десяті, соті, тисячні і т.д. тому людина повинна розуміти, що означають ці дроби, щоб зрозуміти і зробити зв'язок з десятковими знаками.
Ключ до розуміння взаємозв'язку між десятковими числами та дробами (або змішаними числами) починається з правильного ЧИТАННЯ десяткового числа. Більшість людей читають 5.3 як «п'ять пунктів три», що не допомагає зрозуміти його значення. Слід прочитати «п'ять і три десятих». При цьому зв'язок між десятковим 5.3 і змішаним числом\(5 \frac{3}{10}\) зрозуміла. Аналогічно 18.035 слід читати «Вісімнадцять і тридцять п'ять тисячних» і відповідає змішаному числу\(18\frac{35}{1000}\). Ось ще кілька:
- 0.309 і\(\frac{309}{1000}\) обидва правильно прочитані «триста дев'ять тисячних»
- 10.04 і\(10\frac{4}{100}\) обидва правильно прочитані «десять і чотири сотих»
Зверніть увагу, що десяткова крапка читається як «і». Десяткова крапка (і слово «і») відокремлює цілу частину від дробової частини змішаного числа. Це єдино правильне вживання слова «і» при читанні чисел. 760 читається «сімсот шістдесят». Поширена помилка - читати 760 як «сімсот шістдесят». Якщо десяткової крапки немає, не кажіть слово «і».
Люди, які просто дізнаються про десяткові знаки (як діти початкової школи), НЕ повинні читати число 5.4 як «п'ять точок чотири». Це короткий спосіб читання числа, який доречно використовувати лише після того, як хтось дійсно розуміє зв'язок між десятковими числами та дробами. Пам'ятайте, що число, записане в десятковій формі, насправді просто інший спосіб написати змішане число, де знаменник дробової частини - це ступінь десяти! Назва дробової частини (десяті, соті, тисячні і т.д.) - це місце останньої цифри числа після десяткової крапки, яка також буває знаменником числа, записаного в дробовому вигляді.
Подивіться ще раз на 0.309 і\(\frac{309}{1000}\). У десятковій точці три цифри (або значень значень) після десяткової крапки. У дробі є три нулі після 1 (що є числом 1000 в знаменнику). Те ж саме стосується 18.035 і\(18\frac{35}{1000}\). Для 5.3 і\(5\frac{3}{10}\) десяткова кома має одну цифру після коми, а дріб має один нуль після 1. Найкраще, якщо студентам дозволять виявити цей факт для себе. Завжди важливіше відкривати стосунки (які часто стають правилами) самостійно. Студенти, яких регулярно просять правильно читати десяткові, дроби та змішані числа, швидше за все, зроблять це конкретне відкриття самостійно.
Мішані числа, такі як 5.3 і 18.035, також можуть бути записані відразу як неправильні дроби. Знаменник дробу все одно буде таким же, як якщо б він був записаний як змішане число. Чисельник - це число без десяткової крапки взагалі. Наприклад, 5.3 можна записати як\(5\frac{3}{10}\) або\(\frac{53}{10}\); а 18.035 можна записати як\(18\frac{35}{1000}\) або\(\frac{18035}{1000}\).
Зверніть увагу, що коли ви вперше записуєте десяткове число як дріб, це не обов'язково в простій (або зменшеній) формі.
На рядку пропишіть словами, як читати кожен з наступних десяткових знаків. Не використовуйте слово «точка». Потім під ним запишіть кожну десяткову дробу. Якщо число більше або дорівнює 1, спочатку запишіть дріб як змішане число, а потім запишіть його як неправильний дріб. Спрощуйте будь-яку дріб, яка не в найпростішому вигляді. Показати всі кроки (включаючи початкові дроби перед спрощенням).
а. 0,4 _________________________________________________________________
0.4 =
б. 0,26 _________________________________________________________________
0,26 =
c. 3.08 _____________________________________________________________
3.08 =
д. 9,85 _____________________________________________________________
9,85 =
е. 17.305 _________________________________________________________
17,305 =
Запишіть кожен правильний дріб як десятковий. Запишіть кожен неправильний дріб спочатку як змішане число (не зменшуйте), а потім також як десяткове число. Не використовуйте свій калькулятор.
а.\(\frac{14}{100}\) = __________
б.\(\frac{8}{1000}\) = __________
с.\(\frac{435}{100}\) = _______________ = _______________
д.\(\frac{5638}{10}\) = _______________ = _______________
е.\(\frac{305}{100}\) = _______________ = _______________
Правило, яке ви можете запам'ятати для множення дробів, полягає в тому, щоб помножити числа разом, як якщо б не було десяткової крапки, а потім перемістіть десяткову крапку праворуч від загальної кількості місць, в яких вона знаходиться для обох чисел. Наприклад, (8) (0.4) виконується множенням 8 разів 4, а потім переміщенням десяткової крапки в одне місце, щоб отримати 3.2. Аналогічно (0.06) (0.7) робиться множенням 6 разів 7 і переміщенням десяткової крапки в три розряди (два на 0,06 і ще один на 0,7 на загальну суму три), щоб отримати 0,042. Багато людей роблять це важче, ніж насправді, і не розуміють, що вони можуть легко помножити 0,3 і 0,4 в голові. Це так само просто, як 3\(\cdot\) 4 і переміщення десяткової коми в два місця, щоб отримати 0,12. Тепер, як приблизно 1,1 рази 1,2? Це просто 11 разів 12 з десятковим переміщенням у два місця: 1.32.
Давайте поспостерігаємо, чому це правило множення десяткових знаків працює, переписуючи числа як дроби в першу чергу. Ключ тут полягає в тому, щоб записати числа, більші або рівні одиниці, як неправильні дроби. Потім помножте (не скасовуючи і не зменшуючи) дроби. Нарешті, перепишіть дріб як десятковий.
(8) (0,4) =\(\frac{8}{1} \cdot \frac{4}{10} = \frac{32}{10}\) = 3.2 (зверніть увагу, що десяткова крапка - одне місце в для .4)
(1.2) (1.01)\(\frac{12}{10} \cdot \frac{101}{100} = \frac{1212}{1000}\) = 1.212
(Зверніть увагу, що десяткова крапка становить три місця в, один для 1,2 плюс два більше для 1.01)
Помножте наступні десяткові знаки подумки, а відповідь напишіть на бланку. Потім зробіть це ще раз, показуючи ті самі кроки, як показано в попередніх двох прикладах, де кожен десятковий спочатку записується як дріб, потім помножте чисельники та знаменники, а потім перетворіть цю відповідь (не спрощуйте) у десяткову. Не використовуйте свій калькулятор.
а. (0,4) (.07) = ______________
(0.4) (.07) =
б. (1,6) (0,2) = ______________
(1.6) (0.2) =
с. (0,25) (0,3) = ______________
(0,25) (0,3) =
д. (2,2) (0,3) = ______________
(2,2) (0,3) =
Розпізнавання еквівалентних десяткових знаків та порівняння десяткових знаків
Нулі, які знаходяться за останньою ненульовою цифрою десяткового числа, можуть бути додані або видалені без зміни значення десяткового числа. Якщо ви подивитеся на якусь еквівалентну фракцію, ви зрозумієте, чому це має бути правдою. Наприклад,
\[\dfrac{14}{10} = \dfrac{140}{1000} = \dfrac{1400}{10000} = \dfrac{14000}{100000}. \nonumber \]
Всі вони еквівалентні\(\frac{14}{100}\) тому, що чисельник і знаменник був помножений на деяку ступінь 10 (10, 100 або 1000), щоб отримати один з інших еквівалентних дробів. Якщо замінити кожен з чотирьох дробів вище на їх десяткові еквіваленти, то отримаємо 0,14 = 0,14 = 0,140 = 0,1400 = 0,14000. Давайте назвемо будь-які нулі в кінці останньої ненульової цифри десяткової «кінцевої нулі». Тоді ми можемо зробити висновок, що будь-яке число, що починається з .14, що має кінцеві нулі, також еквівалентно, як 0.1400000.
Два десяткових знака рівні лише в тому випадку, якщо один можна зробити так, щоб він виглядав ідентично іншому, додаючи або видаляючи кінцеві нулі. Ви також можете визначити, чи є вони еквівалентними, видаливши надлишкові кінцеві нулі з кожного, щоб побачити, чи вони ідентичні.
Для першого заданого десяткового числа обведіть будь-який з наступних чотирьох десяткових знаків, які дорівнюють йому.
| а. | 1.900; | 1.0900 | 1.9 | 1.90000 | 0,190 |
| б. | 4.034; | 4.0340 | 4.0334 | 4.0034 | 4.3040 |
Щоб порівняти два або більше десяткових знаків, які не рівні, але мають однакову кількість цифр після коми, ви можете написати кожен як дріб з тим же знаменником, а потім порівняти чисельник. Наприклад, 0,14 менше 0,21, оскільки чотирнадцять сотих менше двадцяти сотих. В основному, в даному випадку це так само, як порівняння цілих чисел. Ви зможете визначити, що більше, порівнюючи кожне число, як ніби не було десяткової крапки. Але, майте на увазі, що це має сенс лише в тому випадку, якщо числа, які ви дивитеся на мають однакову кількість цифр після коми.
Порівняйте кожне з наступних десяткових знаків за допомогою <, = or >.
| а. | 3.5 | 0.9 |
| б. | 35.06 | 35.0600 |
| c. | 0.089 | 0.098 |
Щоб порівняти два або більше десяткових знаків, які не рівні, що не всі мають однакову кількість цифр після десяткової крапки, спочатку запишіть кожну десяткову з однаковою кількістю цифр після десяткової крапки (додаючи кінцеві нулі до одного або декількох, якщо це необхідно). Роблячи це, ви порівнюєте десяті з десятими, або соті з сотими тощо, як ви це робили у вправі 5.
Порівняйте кожне з наступних десяткових знаків за допомогою <, = or >.
| а. | 3.51 | 3.488 |
| б. | 35.061 | 35.35 |
| c. | 0.08933 | 0.0894 |
Якщо в знаменнику записується дріб зі степенем десять, то базово записати одне і те ж число в десятковій формі. Ви зробили це у вправі 2. Будь-який дріб, який записаний зі ступенем 10 в знаменнику, може бути записаний як кінцевий десятковий. Це означає, що можна записати число з кінцевими нулями. Але що робити, якщо дріб не має степеня 10 (як 10, 100, 1000 і т.д.) в знаменнику? Іноді це може бути складно!
Якщо дріб БЕЗ степеня десяти в знаменнику МОЖНА записати як еквівалентний дріб ЗІ степенем десяти в знаменнику, то її можна записати як кінцевий десятковий.
Наприклад,\(\frac{1}{2}\) можна записати як\(\frac{5}{10}\) (помноживши чисельник і знаменник на 5)
Тому\(\frac{1}{2}\)\(\frac{5}{10}\) = 0.5 (не забудьте прочитати це як п'ять десятих)
Ну, це було не надто важко, але як щодо\(\frac{7}{80}\)? Питання в тому, чи можна помножити знаменник, 80, на щось, щоб отримати 10, 100, 1000, 10000 і т.д. немає цілого числа можна помножити 80 на, щоб отримати 10, 100 або 1000. Але, якщо помножити 80 разів 125, це дорівнює 100000. Отже, помноживши і 7, і 80 на 125, ми отримаємо еквівалентний дріб,\(\frac{875}{10000}\) для\(\frac{7}{80}\) якого тепер можна записати як десятковий 0,0875.
Як щодо написання\(\frac{5}{6}\) як закінчення десяткової? Ну, немає нічого, що можна помножити 6 на, щоб отримати 10 або 100 або 1000 або 10000. Чи є, можливо, якесь число ми могли б помножити 6 на, щоб отримати деяку вищу потужність десяти? Ну, це гарне питання! Насправді, немає, але як ви могли бути впевнені? Ви, звичайно, не можете спробувати кожну силу десяти, оскільки існує нескінченна кількість їх, щоб спробувати.
Було б непогано, якби був простий спосіб визначити, чи можна записати будь-який заданий дріб як кінцевий десятковий. Ключ полягає в тому, щоб розглянути множники знаменника дробу, які можуть бути записані як кінцевий десятковий. Якщо дріб можна записати як кінцевий десятковий, то існує якийсь еквівалентний дріб, де знаменник повинен бути степенем десяти: 10 або 100 або 1000 і т.д.
Напишіть просту факторизацію кожного з наступних:
а. 10 = _______________
б. 100 = _______________
с. 1000 = _______________
д. 10000 = _______________
е. 100000 = _______________
Які єдині прості множники ступенів 10? ______________
Якщо сила десяти має три фактори 5, скільки факторів 2 вона має? ______
Якщо потужність десяти має два фактори 2, скільки факторів 5 вона має? _____
Повноваження десяти мають лише 2s та 5s як прості фактори та нічого іншого.
Давайте повернемося до наших трьох чисел,\(\frac{1}{2}\),\(\frac{7}{80}\), і\(\frac{5}{6}\), що ми намагалися написати як закінчуючі десяткові знаки і проаналізувати ситуацію.
\(\frac{1}{2}\)спрощується, і в його простому факторованном вигляді в знаменнику є рівно один 2. Щоб записати як еквівалентний дріб зі знаменником, який є степеню десять, він повинен мати тільки 2s і 5s як прості множники в знаменнику, і однакове число кожного! Тому множення ще на 5 в чисельнику і знаменнику зробило хитрість!
Простий множник чисельник і знаменник цього скороченого дробу:\(\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5}\)
Ми повинні визначити, чи можна помножити знаменник на щось, щоб отриманий знаменник складався лише з 2s та 5s та однакового числа кожного. Ну, є чотири фактори 2 і один фактор 5. Оскільки нам потрібно однакове число кожного множника, складання еквівалентного дробу шляхом множення чисельника та знаменника ще на три множника 5 зробить трюк.
\(\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5} \cdot \frac{5 \cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.0875\)
В обох прикладах зверніть увагу, що ми або множимо на додаткові множники 2 або 5, але не обидва!
А як щодо\(\frac{5}{6}\)? Ну, це зменшується, і просте факторизація знаменника 2\(\cdot\) 3. Незалежно від того, на що множиться знаменник, ми будемо застрягати з коефіцієнтом 3 в знаменнику. Оскільки єдиними простими множниками степенів 10 є 2 і 5, у знаменнику не може бути простого множника 3, якщо ми хочемо, щоб в кінцевому підсумку з лише степеню 10 в знаменнику. Тому, оскільки в знаменнику неможливо записати\(\frac{5}{6}\) як еквівалентний дріб зі степенем десять, його не можна записати як закінчувальну десяткову.
Як щодо\(\frac{63}{72}\)? Якщо просте множник знаменника, то отримаємо 2\(\cdot\) 2\(\cdot\) 2\(\cdot\) 3\(\cdot\) 3.
Ну, як ви думаєте? Можна\(\frac{63}{72}\) записати як закінчувальну десяткову? ________
Поясніть, чому чи чому ні.
Один із способів перевірити, що ви отримуєте правильні результати, є використання калькулятора. За\(\frac{1}{2}\), у нас вийшло 0,5, яке ви можете перевірити, виконавши ділення 1\(\div\) 2 на своєму калькуляторі.
Скористайтеся калькулятором, щоб знайти десятковий еквівалент для кожного з наступних параметрів:
а.\(\frac{7}{80}\) = _____________
б.\(\frac{63}{72}\) = _____________
Хммм, ви отримали 0.0875 для частини a? _________
Якщо ви зробили частину b на вашому калькуляторі, ви отримали кінцеву десяткову 0.875?
Це те, що ви очікували? Чому чи чому ні?
Причина\(\frac{63}{72}\) може бути записана як кінцева десяткова, тому що в спрощеному вигляді він має тільки 2 і/або 5 в якості простих множників. Ось як закінчити цю задачу, спростивши спочатку, а потім помноживши на будь-які необхідні множники 2 або 5, щоб отримати однакове число кожного:
\(\frac{63}{72} = \frac{3 \cdot 3 \cdot 7}{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3} = \frac{7}{2 \cdot 2 \cdot 2} \cdot \frac{5\cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.875\)
Для кожного дробу визначте, чи можна його записати як еквівалентний дріб зі ступенем десять в знаменнику. Якщо дріб не може бути записаний як кінцевий десятковий, поясніть, чому б ні. В іншому випадку показуйте ВСІ кроки (як показано в попередніх прикладах), щоб записати їх як термінальну десяткову. Кроки наведені нижче.
- Спрощуйте, якщо це можливо
- Простий коефіцієнт знаменника
- Помножте чисельник і знаменник на відповідну кількість множників 2 або 5, щоб знаменник був степенем 10
- Спрощення чисельника і знаменника
- Запишіть як закінчувальну десяткову
Потім перевірте свою відповідь калькулятором, взявши вихідний дріб і розділивши чисельник на знаменник. Ви повинні отримати той самий десятковий, отриманий, виконавши п'ять кроків, описаних вище.
а.\(\frac{3}{4}\)
б.\(\frac{9}{20}\)
c.\(\frac{9}{15}\)
д.\(\frac{18}{25}\)
е.\(\frac{5}{14}\)
Гаразд, тепер ми маємо справу з тими дробами, які не можуть бути записані як кінцеві десяткові числа. Будь-який спрощений дріб, який має принаймні один простий коефіцієнт, який не є 2 або 5, є в цій категорії. Давайте розглянемо\(\frac{5}{6}\) ще раз. Один із способів записати це як десяткове число - розділити 5 на 6.
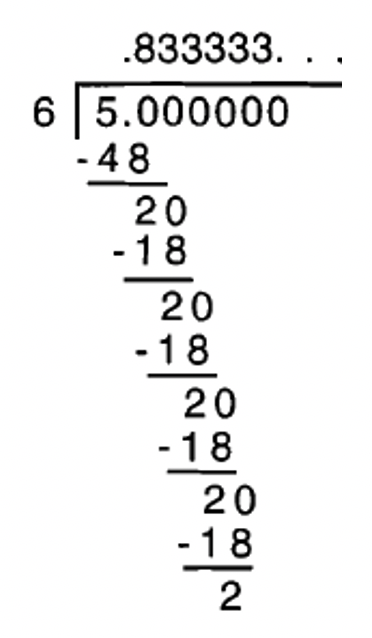
Як ви могли бачити, я продовжую ділити 6 на 20, пишу 3, помножити, щоб отримати 18, відняти від 20, отримати 2, збити 0, і почати все спочатку. Це може тривати на віки віків. Таким чином, 3 в кінці буде слідом назавжди. Це НЕ кінцева десяткова кома, оскільки число не може бути записано з кінцевими нулями. В даному випадку існують задні 3s. Три крапки в кінці (звані еліпсами) числа, щоб показати, що 3 повторюються назавжди. Відповідь можна записати як 0.8333333... або\(0.8\bar{3}\). Не забудьте поставити еліпси (три крапки) в кінці числа! Смуга над 3 вказує на те, що 3 повторюється назавжди і назавжди. Ось інші способи представлення того ж самого:\(0.8\overline{33}\) або\(0.8333\bar{3}\). У першому випадку сказано, що 33 повторюється назавжди. У другому випадку, це говорить після перших трьох 3-х, 3 повторюється назавжди. В обох випадках, коли ви виписуєте його в довгому вигляді, це виглядає як 0.8333333... так що це одне і те ж число. Зазвичай ми напишемо 0.8333333... або\(0.8\bar{3}\).
Напишіть 0.8333333... або ще трьома\(0.8\bar{3}\) способами, відмінними від\(0.8\overline{33}\) або\(0.8333\bar{3}\).
____________________, ____________________, і ____________________
Одна річ, щоб помітити про те, що сталося, коли ми розділили 5 на 6 є те, що я продовжував отримувати 2 після кожного віднімання в діленні, це як залишок. Також пам'ятайте, що при діленні кожен залишок повинен бути меншим або рівним, ніж те, на що ви ділите.
Запишіть можливі залишки для кожного числа.
а. 6: _________________________________
б. 7: _________________________________
c. 9: _________________________________
д. 11: _________________________________
е. 3: _________________________________
Давайте тепер розглянемо, що відбувається, коли ви робите обчислення довгих ділення\(\frac{4}{11}\) і\(\frac{2}{7}\).
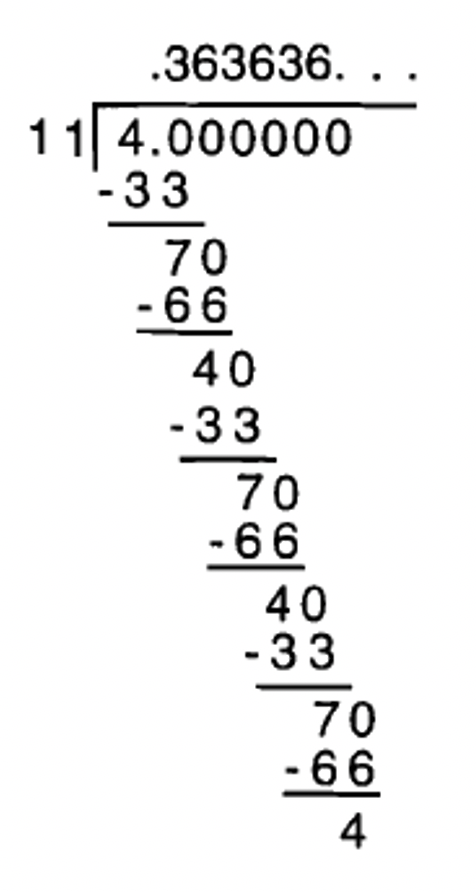 |
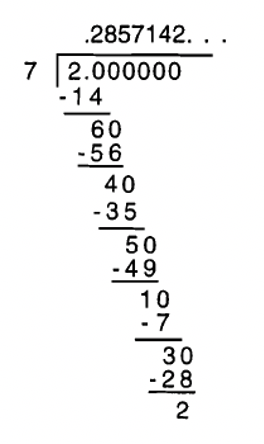 |
В обох цих випадках, врешті-решт, ви отримуєте залишок, який ви отримали раніше, тому обчислення повторюється. У разі ділення 4 на 11 з'являються два залишки, перш ніж буде деякий повторення 4 і 7. З 16d ви повинні були зрозуміти, що єдино можливі залишки для 11 - це 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 і 10. Тепер, якщо ви отримали залишок 0 при діленні, ви б закінчуючи десяткової. Таким чином, при діленні на 11, більшість залишків ви можете отримати в ряд, перш ніж один повтор становить 10 поспіль. Але в разі\(\frac{4}{11}\), залишки повторюються після 4 і 7. Це означає, що ви продовжуєте ділитися на 40 або 70 (оскільки ви приносите нуль вниз), і саме тому в частному цифри починають повторюватися. Не забудьте поставити еліпси (три крапки) в кінці числа, якщо є візерунок повторюваних цифр.
Тепер у випадку ділення 2 на 7, залишки, які ви отримуєте, коли йдете, - це 6, потім 4, потім 5, потім 1, потім 3, а потім 2. Коли ви збиваєте 0, ви знову ділите 7 на 20, а отже, залишки повторюються. Зверніть увагу, що послідовність залишків (6, 4, 5, 1, 3 і 2) відрізняється від послідовності цифр, які повторюються в частці. Цифри, які повторюються в частці, - 285714, так\(\frac{2}{7}\) = 0,285714285714... або\(0.\overline{285714}\).
Оскільки існує лише шість можливих залишків, відмінних від нуля при діленні на 7, лише послідовність з 6 цифр може повторитися. При цьому всі шість можливих залишків 7 з'явилися в довгому діленні.
Існує багато способів вираження нескінченного або повторюваного десяткового 0.285714285714... або\(0.\overline{285714}\). Перш за все, щоб встановити, що повторюється, ви хотіли б бачити послідовність цифр, що повторюються принаймні два рази через. Отже, 0.285714285714... є найкоротшим способом відображення його при використанні еліпсів (трьох крапок). Якщо ви просто написали 0.285714..., не було б зрозуміло, повторюється чи ні 4 або 14 повторюється тощо.
Ось кілька інших способів написати 0.285714285714... крім того\(0.\overline{285714}\).
0.285714285714285714...
0.285714285714 2857142...
(У цьому випадку ви бачите це як 857142, що повторюється з цього моменту)
0.2857142857142857...
(У цьому випадку ви бачите це як 142857, що повторюється з цього моменту)
\(0.28\overline{571428}\)
(У цьому випадку ви бачите це як 571428, що повторюється з цього моменту)
Напишіть 0.285714285714... ще два способи використання еліпсів (три крапки) і ще два способи використання смуги над повторюваною послідовністю цифр.
Визначте, що з наступного еквівалентно 0.383432432432...
Один із способів зробити це - записати номер у довгій формі, ретельно продовжуючи візерунок, а потім перевіряйте цифри по одному місці за раз.
- 0.3834324324...
- 0.383432432...
- 0.3834323432...
- \(0.38343\overline{243}\)
- \(0.38\overline{34324}\)
Майте на увазі, що якщо ви знаходите десятковий еквівалент для дробу з 17 в знаменнику, то перед тим, як ви побачите повторення, може бути до шістнадцяти цифр поспіль. Тепер, очевидно, є тільки 10 цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) в базовій десятці. Зверніть увагу, що послідовність цифр, що повторюються в частці, абсолютно відрізняється від можливих залишків, які ви можете отримати, коли ви ділите на 17, оскільки залишок може бути більше, ніж однозначне число.
а Скільки можливих залишків може бути, якщо розділити число на 33?
b. робити довге ділення, щоб записати\(\frac{31}{33}\) як повторювану десяткову з використанням еліпсів, а потім використовуючи смугу над повторюваними цифрами в цьому рядку: __________________________________
Показувати роботу тут:
c При довгому діленні, скільки цифр повторюється? ______
d У довгому поділі, які залишки ви б продовжували отримувати, якщо ви продовжували поділ назавжди? _________________
Використовуйте калькулятор, щоб написати кожен як повторюваний десятковий. Напишіть відповідь двома способами, спочатку смужкою над повторюваними цифрами, а потім в довгій формі, використовуючи еліпси. Зверніть увагу, що ваш калькулятор може округлити або не округлити останню показану цифру. Він не може відображати цифри, що повторюються назавжди, тому ви повинні бути достатньо кмітливими, щоб знати, чи десяткове показ на дисплеї є терміналом, чи це наближення.
а.\(\frac{5}{9}\) = ________________ = _______________________________
б.\(\frac{5}{7}\) = ________________ = _______________________________
в.\(\frac{1}{6}\) = ________________ = ___________________________________
д.\(\frac{2}{3}\) = ________________ = _______________________________
е.\(\frac{7}{11}\) = ________________ = _______________________________
ф.\(\frac{5}{12}\) = ________________ = _______________________________
г.\(\frac{8}{15}\) = ________________ = _______________________________
ч.\(\frac{16}{45}\) = ________________ = _______________________________
i.\(\frac{5}{66}\) = ________________ = _______________________________
Якщо ви змінюєте спрощений дріб на десятковий, де знаменник дорівнює x, скільки цифр не більше може повторюватися в частному? _________
Ну, ви дізналися, як писати кінцеві десяткові дроби як дроби, і як писати дроби як десяткові. Ви повинні мати можливість визначити, чи можна записати дріб як кінцевий або повторюваний десятковий, перш ніж робити фактичне ділення.
Раціональні числа визначаються як числа, які можуть бути виражені у співвідношенні двох цілих чисел. Дроби, як ми зазвичай посилаємося на них (без десяткових крапок або квадратних коренів і т.д. в чисельнику або знаменнику) є раціональними числами. Оскільки всі дроби можуть бути записані як кінцеві або нескінченні (нескінченні, повторювані) десяткові, то всі кінцеві і повторювані десяткові числа також є раціональними числами. У вправі 1 ви написали деякі кінцеві десяткові дроби як дроби. Оскільки всі некінцеві десяткові числа прийшли з дробу, тепер ми хочемо мати можливість піти навпаки і написати повторюваний десятковий як дріб. У нас є чудовий трюк для того, щоб зробити саме це!
Скажімо, ми хотіли написати\(0.\overline{72}\) або 0.7272727272... як дріб.
По-перше, зверніть увагу, що це зовсім інше число від 0.72, оскільки 0.72 - сімдесят дві соті, або\(\frac{72}{100}\). Це спрощує\(\frac{18}{25}\). Так, 0 .72 і\(\frac{18}{25}\) є однаковим числом. Ви можете перевірити, щоб переконатися в\(\frac{18}{25}\) правильності дробу, скориставшись калькулятором і розділивши 18 на 25. Калькулятор повинен читати 0.72, з чого ми і почали.
Гаразд, так як ми пишемо\(0.\overline{72}\) як дріб? Оскільки це повторювана десяткова кома, яка має нескінченно багато цифр, немає єдиної потужності десяти, яку ми можемо поставити в знаменник. Хитрість полягає в тому, щоб використовувати алгебру для запису числа таким чином, що усуває нескінченно повторювану частину десяткового числа. Для початку\(0.\overline{72}\) випишемо довгий шлях:
\(0.\overline{72}\)= .727272727272... і назвіть його числом х, так x = 0.72727272727272...
Пам'ятайте, що якщо помножити десяткову крапку на 10, десяткова крапка переміщається на одне місце вправо, а при множенні десяткової крапки на 100 десяткова крапка переміщається на два розряди вправо і т.д.
Якщо х = 0,727272727272..., то випишіть, що дорівнює 10х, 100х і 1000х. Випишіть його, не використовуючи смужку над повторюваними цифрами. Використовуйте еліпси (три крапки).
10х = _______________________________
100х = _______________________________
1000х = _______________________________
Гаразд, давайте працювати з х = 0.727272727272... і 100х = 72.727272727272...
а. в алгебрі, що таке 100х - х? _________ (Підказка: Відніміть коефіцієнти.)
б Обчислити 100х - х іншим способом: вирівняти десяткові крапки і відняти 0.727272727272... з 72.7272727272... Зверніть увагу, що якщо десяткові знаки вишикувалися, «хвости» в кінці обох повторюваних десяткових знаків точно однакові, тому їх слід легко відняти. Покажіть роботу нижче.
c. Напишіть рівняння таким чином, щоб відповідь на частину a дорівнювала відповіді на частину b. Потім скористайтеся алгеброю для розв'язання x. Показати роботу.
d Спростіть дріб, який ви отримали для x в частині c Показати роботу.
e Використовуйте калькулятор, щоб переписати дріб, який ви отримали в частині c, як десятковий:
Чи дорівнює вона\(0.\overline{72}\)? __________
Якщо так, ви повинні були написати\(0.\overline{72}\) як правильний дріб!
Ось хитрість для зміни повторюваних десяткових знаків на спрощені дроби:
Викличте число, яке ви намагаєтеся записати у вигляді десяткової змінної, як\(n\) або x.
Якщо є одна повторювана цифра, обчислити 10x; якщо є дві повторювані цифри, обчислити 100x; якщо є три повторювані цифри, обчислити 1000x тощо Це вирівнює повторювані десяткові знаки між собою так, щоб хвіст x та інше число (10x, 100x, 1000x і т.д.) однакове.
Потім відніміть х з іншого числа (10x, 100x, 1000x і т.д.) Хвости обох чисел відірвуться, і у вас повинна бути алгебраїчна задача, яку потрібно вирішити на цьому етапі. Переконайтеся, що ви пишете свою відповідь у вигляді скороченого дробу з лише цілими числами в чисельнику та знаменнику.
Ось два приклади. Якщо ви пишете число в десятковій формі без смужки над числом, не забудьте поставити еліпси (три крапки) в кінці!
|
Пишіть\(0.\bar{2}\) як спрощений дріб. Нехай х\(0.\bar{2}\) = .222222... Так як повторюється тільки одна цифра, помножте х на 10. Тоді 10х = 2,222222... \[\begin{aligned} 10x = & 2.22222.... \\ - x = & .2222..... \\ \hline 9x = & 2 \end{aligned} \nonumber \] \[x = \frac{2}{9}\nonumber \] Використовуйте калькулятор, щоб перевірити це\(\frac{2}{9} = 0.\bar{2}\) |
Пишіть\(0.\overline{54}\) як спрощений дріб. Нехай х\(0.\overline{54}\) = .545454... Так як дві цифри повторюються, помножте х на 100. Тоді 100х = 54,545454... \[\begin{aligned} 100x = & 54.545454... \\ - x = & .545454... \\ \hline 99x = & 54 \end{aligned} \nonumber \] \[x = \frac{54}{99} = \frac{6}{11}\nonumber \] Використовуйте калькулятор, щоб перевірити це\(\frac{6}{11} = 0.\overline{54}\) |
Перепишіть кожен з наступних десяткових знаків як спрощені дроби. Для повторення десяткових знаків використовуйте техніку, показану в попередніх прикладах. Потім перевірте свою відповідь за допомогою калькулятора, розділивши чисельник на знаменник, щоб побачити, чи відповідає результат початковій задачі.
а. 0,4
б\(0.\bar{4}\) Почніть з дозволу х =\(0.\bar{4}\) або х = 0,44444...
с. 0,06 =
d\(0.\overline{06}\) Почніть з дозволу х =\(0.\overline{06}\) або х = 0,060606...
е. 0,9
f\(0.\bar{9}\) Почніть з дозволу х =\(0.\bar{9}\) або х = 0,9999... (ця відповідь може вас здивувати)
г. 0,45
h\(0.\overline{45}\) Почніть з дозволу х =\(0.\overline{45}\) або х = 0,454545...
я. 0,084
j\(0.\overline{084}\) Почніть з дозволу х =\(0.\overline{084}\) або 0.084084084...
Іноді арифметика стає трохи складнішою. Розглянемо написання 0.14444... як дріб. 4 повторюється, починаючи з двох знаків після коми. Ми занурюємося вперед, як і раніше, але є невеликий глюк в кінці, тому що одна сторона рівняння буде мати десяткову крапку в ньому. Якби ми розділили на 9, дріб буде мати десяткову крапку в чисельнику, так що це не зменшене раціональне число; і чисельник, і знаменник повинні бути цілими числами. Ось основні кроки до цього моменту.
\(10n = 1.444444...\)і\(n = 0.144444\)
Віднімаючи, отримуємо\(9n = 1.3\)
Один із способів виправити цю ситуацію - помножити обидві сторони рівняння на 10 (або 100 або 1000 за потребою), щоб усунути десяткове число. Це схоже на очищення дробів шляхом множення обох сторін рівняння на найменш спільний знаменник.
Так помножте обидві сторони\(9n = 1.3\) на 10, щоб отримати\(90n = 13\). Потім розділіть на 90, щоб отримати\(\frac{13}{90}\).
Ще один спосіб виправити цю ситуацію - написати праву частину рівняння у вигляді дробу. Пам'ятайте, що 1.3 - це\(\frac{13}{10}\). Отже, рівняння є\(9n=\frac{13}{10}\).
Ви можете перехресно множити, щоб отримати,\(90n = 13\) а потім розділити на 90, щоб отримати\(n = \frac{13}{90}\)
У будь-якому випадку пам'ятайте, що зменшений дріб - це відношення двох цілих чисел, які є відносно простими.
Перепишіть кожен повторюваний десятковий, використовуйте техніку, показану в попередньому прикладі, як спрощений дріб. Потім за допомогою калькулятора розділіть чисельник на знаменник і подивіться, чи відповідає результат початковій задачі.
а. 0.02828...
б. 0,2888...
c. 0,00666...
д. 0.1011011...
е. 0,3999...
Отже, що ви думали про відповідь на 24f і 25e? Обидва вони трохи запаморочливі. Це важко прийняти, але 0.999999... насправді таке ж число, як 1. Це не менше 1 це рівно 1! Для 24f, якщо пустити\(10n = 9.999...\) і\(n =0 .999...\), то віднімаючи\(n\) з\(10n\) врожайності\(9n = 9\), так\(n = 1\). Це важко проковтнути, але це правда! Інший спосіб побачити це - усвідомити, що 1/3 + 2/3 = 1. Але 1/3 = 0,333333... і 2/3 = 0,666666... Потім 1/3 + 2/3 = 0,33333... + 0,66666... = 0,99999... Ми знаємо 1/4 + 2/3 = 1, тому 0.99999... також повинен дорівнювати 1, а також. О, цей матеріал просто занадто крутий!
Для 0.39999... результат повторення 9s після десяткового числа складає 0.39999... = 0.4 =\(\frac{4}{10} = \frac{2}{5}\).
Таким чином, в основному, будь-яке число з купою кінцевих 9s закінчується тим, що закінчується десяткової.
Всі числа, з якими ми мали справу до цих пір дробів, закінчуючи десяткові, і повторювані десяткові числа складають раціональні числа. Кожне раціональне число може бути записано як співвідношення двох відносно простих цілих чисел, а також може бути записано як кінцеве або повторюване десяткове число. І навпаки, кожне закінчення і повторення десяткового числа є раціональним числом.
О, але є ще... набагато більше!
Раціональні складають дуже малу частину дійсних чисел. Щоб завершити реальну систему числення, ми повинні говорити про ірраціональні числа. Кожне дійсне число є або раціональним, або ірраціональним. Ті числа, які не можна записати як співвідношення двох відносно простих цілих чисел, є ірраціональними. Ті десяткові числа, які не закінчуються і не повторюються, є ірраціональними. Отже, як вони виглядають?
Одним з найбільш відомих ірраціональних чисел є\(\pi\). Саме число є відношенням окружності кола до його діаметру. Схоже, що це співвідношення двох цілих чисел, але це не так! \(\pi\)може бути тільки наближений. Найбільш поширене наближення - 3,14 або 22/7. Жоден з них не дорівнює\(\pi\) тому, що обидва вони є раціональними числами, і\(\pi\) ні!
Інші ірраціональні числа - це квадратні корені чисел, які не є ідеальними квадратами, або кубові корені чисел, які не є ідеальними кубами тощо.
Наприклад, ці цифри нераціональні:\( \sqrt{5}, \sqrt{3}, \sqrt{12}, \sqrt{20}, \sqrt[3]{35}, \sqrt[4]{72}\)
Напишіть п'ять ірраціональних чисел, ще не перерахованих вище ________________________
Чи\(\sqrt{9}\) нераціонально? _____ Чому чи чому ні? ________________________________
Інший спосіб висловити ірраціональне число в десятковій формі - це скласти десяткове число, яке, можливо, має певний шаблон до нього, але ніколи не закінчується або повторюється. Два приклади цього типу - 2.12112111211112... і 5.010203040506070809010011012...
Запишіть чотири ірраціональних числа в десятковій формі, що показує чітку закономірність.
Запишіть як раціональне число, так і ірраціональне число в десятковій формі, що знаходиться між 0,53 і 0,54.
Запишіть як раціональне число, так і ірраціональне число в десятковій формі, що знаходиться між 0.53333... і 0.54444...
Раціональний ______________________
Ірраціональний ______________________
Класифікуйте кожне з наступних чисел як раціональне або ірраціональне.
а. 0,428222... ___________________
б. 0,283848... ___________________
c.\(\frac{5}{13}\) ___________________
д.\(\sqrt{80}\) ___________________
е.\(\sqrt{100}\) ___________________
ф.\(\pi\) ___________________
