Skip to main content
LibreTexts - Ukrayinska

1.8: Десяткові

  1. Last updated
  2. Save as PDF
  • Page ID
    59088

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Ім'я і запис десяткових знаків
    • Круглі десяткові
    • Додавання та віднімання десяткових знаків
    • Множення і ділення десяткових знаків
    • Перетворення десяткових знаків, дробів та відсотків
    Примітка

    Більш ретельне ознайомлення з темами, розглянутими в цьому розділі, можна знайти в розділі Преалгебра, Десяткові числа.

    Ім'я та запис десяткових знаків

    Десяткові числа - це ще один спосіб запису дробу s, знаменниками яких є повноваження 10.

    \[\begin{array} {ll} {0.1 = \frac { 1 } { 10 }} &{0.1 \text { is "one tenth" }} \\ {0.01 = \frac { 1 } { 100 }} &{0.01 \text { is "one hundredth }} \\ {0.001 = \frac { 1 } { 1,000 }} &{0.001 \text { is "one thousandth }} \\ {0.0001 = \frac { 1 } { 10,000 }} &{0.0001 \text { is "one ten-thousandth" }} \end{array}\]

    Зверніть увагу, що «десять тисяч» - це число більше одиниці, але «одна десятитисячна» - це число менше одиниці. «й» в кінці назви говорить про те, що число менше одиниці.

    Коли ми називаємо ціле число, ім'я відповідає значенню місця на основі степеней десяти. Ми читаємо 10 000 як «десять тисяч» і 10 000 000 як «десять мільйонів». Аналогічним чином імена десяткових знаків відповідають їх значенням дробу. \(\PageIndex{1}\)На малюнку показані назви значень місць зліва і праворуч від десяткової крапки.

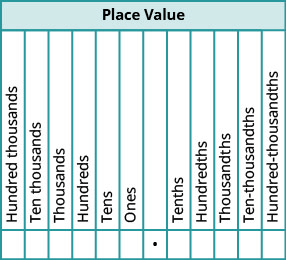
    Буде показано таблицю з назвою Place Value. Зліва направо рядок читає «Сто тисяч», «Десять тисяч», «Тисячі», «Сотні», «Десятки» і «Одиниці». Потім є порожня комірка, а під нею знаходиться десяткова крапка. Праворуч від цього клітини читають «Десяті», «Соті», «Тисячні», «Десятитисячні» і «Стотисячні».
    Малюнок\(\PageIndex{1}\): Значення місця десяткових чисел відображаються ліворуч і праворуч від десяткової крапки.
    Вправа\(\PageIndex{1}\)

    Назвіть десяткове число\(4.3\).

    Відповідь

    Наводиться таблиця з чотирма кроками. Додатково наведено число 4.3. Перший крок говорить «Крок 1. Назвіть число ліворуч від десяткової крапки.» Праворуч від цього зазначається, що «4 знаходиться зліва від десяткової крапки». Праворуч від цього він читає «чотири», а потім великий порожній пробіл.Другий крок говорить «Крок 2. Запишіть «і» для десяткової крапки.» Праворуч від цього він читає «чотири і», а потім порожній пробіл.Третій крок говорить «Крок 3. Назвіть частину «number» праворуч від десяткової крапки так, ніби це ціле число.» Праворуч від цього він читає «3 праворуч від десяткової крапки». Праворуч від цього написано «чотири і три», а потім порожній.Нарешті, останній крок говорить «Крок 4. Назвіть десятковий розряд.» Праворуч від цього написано «чотири і три десяті».

    Вправа\(\PageIndex{2}\)

    Назвіть десяткове число\(6.7\).

    Відповідь

    шість і сім десятих

    Вправа\(\PageIndex{3}\)

    Назвіть десяткове число\(5.8\).

    Відповідь

    п'ять і вісім десятих

    Ми підсумовуємо кроки, необхідні для назви десяткового числа нижче.

    НАЗВА ДЕСЯТКОВОГО.
    1. Назвіть число ліворуч від десяткової крапки.
    2. Запишіть «і» для десяткової крапки.
    3. Назвіть частину «число» праворуч від десяткової крапки так, ніби це ціле число.
    4. Назвіть десятковий розряд останньої цифри.
    Вправа\(\PageIndex{4}\)

    Назвіть десяткове:\(−15.571\).

    Відповідь
      \(−15.571\)
    Назвіть число ліворуч від десяткової крапки. негативні п'ятнадцять __________________________________
    Запишіть «і» для десяткової крапки. негативні п'ятнадцять і __________________________________
    Назвіть число праворуч від десяткової крапки. негативні п'ятнадцять і п'ятсот сімдесят один __________
    The\(1\) знаходиться в тисячному місці. негативні п'ятнадцять і п'ятсот сімдесят одна тисячна
    Вправа\(\PageIndex{5}\)

    Назвіть десяткове:\(−13.461\).

    Відповідь

    негативні тринадцять і чотириста шестьдесят одна тисячна

    Вправа\(\PageIndex{6}\)

    Назвіть десяткове:\(−2.053\).

    Відповідь

    негативні дво- і пятьдесят тритисячні

    Коли ми пишемо чек, пишемо як числівники, так і назву числа. Давайте подивимося, як записати десяткове з імені.

    Вправа\(\PageIndex{7}\): How to Write decimals

    Напишіть «чотирнадцять і двадцять чотири тисячні» як десяткове число.

    Відповідь

    Наводиться таблиця з чотирма кроками. Перший крок говорить «Крок 1. Шукайте роботу «і» — вона знаходить десяткову крапку. Поставте десяткову крапку під словом «і'. Перекладіть слова перед «і» в ціле число і помістіть його ліворуч від десяткової крапки.» Праворуч від цього у нас є слова «чотирнадцять і двадцять чотири тисячні». Під цим словом ми маємо «чотирнадцять і двадцять чотири тисячні» зі словом «і» підкреслено. Під цим словом ми маємо невеликий порожній пробіл, відокремлений від більшого пробілу десятковою крапкою. Під цим у нас є 14 у маленькому порожньому просторі, за яким слідує десяткова крапка та більший порожній простір.Другий крок говорить «Крок 2. Відзначте потрібну кількість десяткових знаків праворуч від десяткової крапки, зазначивши значення місця, зазначене останнім словом.» Праворуч від цього написано «Останнє слово - тисячні». Праворуч від цього є число 14, за яким слідує десяткова крапка і три невеликі пробіли. Під порожніми пробілами пишуться слова «десяті», «соті» і «тисячні».Третій крок говорить «Крок 3. Переведіть слова після «і» в число праворуч від десяткової крапки. Запишіть число в пробілах — поставивши кінцеву цифру на останнє місце». Праворуч від цього, у нас є 14 після десяткової, а потім порожній пробіл, а потім 2 і 4 на інших двох раніше порожніх пробілах.Нарешті, останній крок говорить «Крок 4. Заповніть нулі для власників порожніх місць у міру необхідності». Праворуч від цього написано «Нулі потрібні на десятому місці». Праворуч від цього, у нас є 14 після коми, а потім 0, 2 і 4, відповідно, на порожніх пробілах. Нижче цього ми маємо «чотирнадцять і двадцять чотири тисячні написано 14.024».

    Вправа\(\PageIndex{8}\)

    Пишіть як десяткове число: тринадцять і шестьдесят вісім тисячних.

    Відповідь

    13.068

    Вправа\(\PageIndex{9}\)

    Запишіть як десяткове число: п'ять і дев'яносто чотири тисячні.

    Відповідь

    5.094

    Підсумовуємо кроки до написання десяткового числа.

    НАПИШІТЬ ДЕСЯТКОВУ.
    1. Шукайте слово «і» —воно знаходить десяткову крапку.
      • Поставте десяткову крапку під словом «і». Переведіть слова перед «і» в ціле число і помістіть його зліва від десяткової крапки.
      • Якщо немає «і», напишіть «0» з десятковою крапкою праворуч.
    2. Відзначте потрібну кількість десяткових знаків праворуч від десяткової крапки, зазначивши значення місця, зазначене останнім словом.
    3. Переведіть слова після «і» в число праворуч від десяткової крапки. Запишіть число в пробілах - поставивши остаточну цифру на останнє місце.
    4. Заповніть нулі для власників місць у міру необхідності.

    Круглі десяткові

    Округлення десяткових знаків дуже схоже на округлення цілих чисел. Ми будемо округлити десяткові числа методом, заснованим на тому, який ми використовували для округлення цілих чисел.

    Вправа\(\PageIndex{10}\)

    Округлення 18.379 до найближчої сотої.

    Відповідь

    Наводиться таблиця з чотирма кроками. Перший крок говорить «Крок 1: Знайдіть задане значення місця і позначте його стрілкою». Праворуч від цього, ми маємо число 18.379; над ним, є слова сотні місце, яке має стрілку, що вказує на 7.Другий крок говорить «Крок 2. Підкресліть цифру праворуч від заданого значення місця.» Праворуч від цього ми маємо 18.379 з 9 підкресленими.Третій крок говорить «Крок 3. Ця цифра більше або дорівнює 5? Нижче написано: «Так: додайте 1 до цифри в даному місці значення». Нижче написано: «Ні: не змінюйте цифру в даному місці значення». Праворуч від цього написано «Оскільки 9 більше або дорівнює» Праворуч від цього у нас є число 18.379 з позначкою 9 «видалити» та 7 з позначкою «додати 1».Нарешті, останній крок говорить «Крок 4. Перепишіть число, прибравши всі цифри праворуч від округлення цифри». Праворуч від цього ми маємо 18.38, а потім «18.38 - 18.379 округлено до найближчої сотої».

    Вправа\(\PageIndex{11}\)

    Округлення до найближчої сотої: 1.047.

    Відповідь

    1.05

    Вправа\(\PageIndex{12}\)

    Округлення до найближчої сотої: 9.173.

    Відповідь

    9.17

    Тут ми підсумовуємо кроки для округлення десяткового числа.

    КРУГЛІ ДЕСЯТКОВІ ЗНАКИ.
    1. Знайдіть задане значення місця і позначте його стрілкою.
    2. Підкресліть цифру праворуч від значення місця.
    3. Ця цифра більше або дорівнює 5?
      • Так — додайте 1 до цифри у вказаному значенні місця.
      • Ні — не змінюйте цифру в заданому місці.
    4. Перепишіть число, видаливши всі цифри праворуч від округлення цифри.
    Вправа\(\PageIndex{13}\)

    Круглий 18.379 до найближчого

    1. десятий
    2. ціле число.
    Відповідь

    Круглий 18.379

    1. до найближчої десятої

    Знайдіть десяте місце за допомогою стрілки. .
    Підкресліть цифру праворуч від заданого значення місця. .
    Оскільки 7 більше або дорівнює 5, додайте 1 до 3. .
    Перепишіть число, видаливши всі цифри праворуч від округлення цифри. .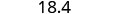
    Зверніть увагу, що видалені цифри НЕ були замінені нулями. Так, 18,379 округлено до найближчої десятої дорівнює 18,4.


    2. до найближчого цілого числа
    Знайдіть ті місця за допомогою стрілки. .
    Підкресліть цифру праворуч від заданого значення місця. .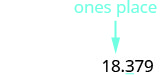
    Оскільки 3 не більше або дорівнює 5, не додавайте 1 до 8. .
    Перепишіть число, видаливши всі цифри праворуч від округлення цифри. .
      Отже, 18,379 округляється до найближчого цілого числа - 18.
    Вправа\(\PageIndex{14}\)

    Округлення 6.582 до найближчого

    1. сотий
    2. десятий
    3. ціле число.
    Відповідь
    1. 6.58
    2. 6.6
    3. 7
    Вправа\(\PageIndex{15}\)

    Круглий 15.2175 до найближчого

    1. тисячного
    2. сотий
    3. десятий.
    Відповідь
    1. 15.218
    2. 15.22
    3. 15.2

    Додавання та віднімання десяткових знаків

    Щоб додати або відняти десяткові числа, ми вибудовуємо десяткові крапки. Вибудовуючи десяткові крапки таким чином, ми можемо додати або відняти відповідні значення місця. Потім ми додаємо або віднімаємо числа так, ніби вони були цілими числами, а потім розміщуємо десяткову крапку в сумі.

    ДОДАЙТЕ АБО ВІДНІМАЙТЕ ДЕСЯТКОВІ ЗНАКИ.
    1. Запишіть числа так, щоб десяткові крапки вибудовувалися вертикально.
    2. Використовуйте нулі в якості власників місця, якщо потрібно.
    3. Додайте або відніміть числа так, ніби вони цілі числа. Потім помістіть десяткову крапку у відповіді під десятковими крапками в заданих числах.
    Вправа\(\PageIndex{16}\)

    Додати:\(23.5+41.38\).

    Відповідь

    \[\text{Write the numbers so that the decimal points line up vertically.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
    \[\text{Put 0 as a placeholder after the 5 in 23.5. Remember, } \frac{5}{10} = \frac{50}{100}, \text{ so } 0.5 = 0.50 \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
    \[\text{Add the numbers as if they were whole numbers . Then place the decimal point in the sum.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline 64.88 \end{array}\]

    Вправа\(\PageIndex{17}\)

    Додати:\(4.8+11.69\).

    Відповідь

    \(16.49\)

    Вправа\(\PageIndex{18}\)

    Додати:\(5.123+18.47\).

    Відповідь

    \(23.593\)

    Вправа\(\PageIndex{19}\)

    Відніміть:\(20−14.65\).

    Відповідь

    \[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {20 - 14.65} \\ {20.} \\ {-14.65} \\ \hline \end{align}} \\ {\text{Remember, 20 is a whole number, so place the decimal point after the 0.}} &{} \end{array}\]
    \[\begin{array} {ll} {\text{Put zeros to the right as placeholders.}} &{ \begin{align} {20.00} \\ {-14.65} \\ \hline \end{align}} \end{array}\]
    \[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {\tiny{9} \quad \tiny{9}\qquad} \\ {\small{1} \not{\small{10}} \not{\small10}\not{\small10}}\\ {\not{2}\not{0.}\not{0}\not{0}} \\ {-14.65} \\ \hline \\{5.35} \end{align}} \end{array}\]

    Вправа\(\PageIndex{20}\)

    Відніміть:\(10−9.58\).

    Відповідь

    0,42

    Вправа\(\PageIndex{21}\)

    Відніміть:\(50−37.42\).

    Відповідь

    12.58

    Множення та ділення десяткових знаків

    Множення десяткових знаків дуже схоже на множення цілих чисел - ми просто повинні визначити, де розмістити десяткову крапку. Процедура множення десяткових знаків матиме сенс, якщо ми спочатку перетворимо їх в дроби, а потім множимо.

    Отже, давайте подивимося, що ми отримаємо як добуток десяткових знаків, перетворюючи їх у дроби в першу чергу. Ми зробимо два приклади пліч-о-пліч. Шукайте викрійку!

      .

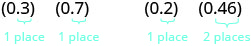    Перетворити на дроби.    		 .
    Помножити. .
    Перетворити на десяткові знаки. .
    Таблиця\(\PageIndex{1}\)

    Зверніть увагу, в першому прикладі ми помножили два числа, щоб кожен мав одну цифру після десяткової крапки і твір мав два знака після коми. У другому прикладі ми помножили число з одним десятковим знаком на число з двома знаками після коми і добуток мав три знака після коми.

    Ми множимо числа так само, як ми робимо цілі числа, тимчасово ігноруючи десяткову крапку. Потім ми підраховуємо кількість десяткових крапок у множниках, і ця сума говорить нам кількість десяткових знаків у добутку.

    Правила множення позитивних і негативних чисел стосуються і десяткових знаків теж, звичайно!

    При множенні двох чисел

    • якщо їх ознаки однакові, продукт позитивний.
    • якщо їх ознаки різні, продукт негативний.

    Коли ми множимо знакові десяткові числа, спочатку визначаємо знак добутку, а потім множимо так, ніби числа обидва позитивні. Нарешті, пишемо виріб відповідним знаком.

    МНОЖТЕ ДЕСЯТКОВІ ЗНАКИ.
    1. Визначте ознаку вироби.
    2. Пишіть у вертикальному форматі, вишикуючи цифри праворуч. Помножте числа так, ніби вони цілі числа, тимчасово ігноруючи десяткові крапки.
    3. Розставте десяткову крапку. Число десяткових знаків у добутку - це сума кількості десяткових знаків у множниках.
    4. Напишіть виріб відповідним знаком.
    Вправа\(\PageIndex{22}\)

    Помножити:\((−3.9)(4.075)\).

    Відповідь
      \((−3.9)(4.075)\)
    Прикмети різні. Продукт буде негативним.  
    Пишіть у вертикальному форматі, вишикуючи цифри праворуч. .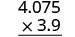
    Помножити. .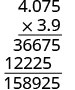
    Додайте кількість десяткових знаків у множниках\((1 + 3)\).

    .
    Поставте десяткову крапку на 4 розряди праворуч.    		 .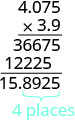
    Ознаки різні, тому продукт негативний. \((−3.9)(4.075) = −15.8925\)
    Вправа\(\PageIndex{23}\)

    Помножити:\(−4.5(6.107)\).

    Відповідь

    \(−27.4815\)

    Вправа\(\PageIndex{24}\)

    Помножити: −10,79 (8,12).

    Відповідь

    \(−87.6148\)

    У багатьох інших класах, особливо в науках, ви будете множити десяткові числа на ступені 10 (10, 100, 1000 тощо). Якщо помножити кілька виробів на папері, ви можете помітити закономірність, що стосується кількості нулів у степені 10 до числа десяткових знаків, ми переміщаємо десяткову крапку вправо, щоб отримати твір.

    ПОМНОЖТЕ ДЕСЯТКОВУ КОМУ НА СТУПІНЬ ДЕСЯТЬ.
    1. Перемістіть десяткову крапку вправо на ту ж кількість знаків, що і кількість нулів в ступені 10.
    2. Додайте нулі в кінці числа за потребою.
    Вправа\(\PageIndex{25}\)

    Помножити 5,63

    1. на 10
    2. на 100
    3. на 1000.
    Відповідь

    Дивлячись на кількість нулів, кратних десяти, ми бачимо кількість знаків, які нам потрібно перемістити десяткове вправо.

    ⓐ

      \(5.63(10)\)
    Існує 1 нуль в 10, тому перемістіть десяткову крапку на 1 місце вправо. .

    ⓑ

      \(5.63(100)\)
    Є 2 нулі в 100, тому перемістіть десяткову крапку на 2 розряди вправо. .

    ⓒ

       
    Є 3 нулі в 1000, тому перемістіть десяткову крапку на 3 місця вправо. .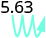
    В кінці потрібно додати нуль. .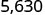
    Вправа\(\PageIndex{26}\)

    Помножити 2,58

    1. на 10
    2. на 100
    3. на 1000.
    Відповідь
    1. 25.8
    2. 258
    3. 2 580
    Вправа\(\PageIndex{27}\)

    Помножити 14,2

    1. на 10
    2. на 100
    3. на 1000.
    Відповідь
    1. 142
    2. 1 420
    3. 14 200

    Так само, як і при множенні, ділення десяткових знаків дуже схоже на ділення цілих чисел. Ми просто повинні з'ясувати, де десяткова крапка повинна бути розміщена.

    Щоб розділити десяткові числа, визначте, на яку потужність 10 помножити знаменник, щоб зробити його цілим числом. Потім помножте чисельник на ту саму потужність 10. Через еквівалентну властивість fractions ми не змінили значення дробу! Ефект полягає в переміщенні десяткових крапок в чисельнику і знаменнику на однакову кількість знаків вправо. Наприклад:

    \[\begin{array} { c } { \frac { 0.8 } { 0.4 } } \\ { \frac { 0.8 ( 10 ) } { 0.4 ( 10 ) } } \\ { \frac { 8 } { 4 } } \end{array}\]

    Ми також використовуємо правила поділу позитивних і негативних чисел десятковими числами. При діленні знакових десяткових знаків спочатку визначте знак частки, а потім діліть так, ніби числа обидва позитивні. Нарешті, напишіть частку відповідним знаком.

    Ми переглядаємо позначення та словниковий запас для поділу:

    \[\begin{array} {ll} {} &{\underset{\text{quotient}}{c}} \\ {\underset{\text{dividend}}{a} \div \underset{\text{divisor}}{b} = \underset{\text{quotient}}{c}} & {\underset{\text{divisor}}{b})\overline{\underset{\text{dividend}}{a}}} \end{array}\]

    Ми напишемо кроки, які потрібно зробити при діленні десяткових знаків, для зручності довідки.

    ДІЛИМО ДЕСЯТКОВІ ЗНАКИ.
    1. Визначте ознаку частки.
    2. Зробіть дільник цілим числом, «перемістивши» десяткову крапку вправо. «Перемістіть» десяткову крапку в дивіденді на ту саму кількість місць - додаючи нулі за потребою.
    3. Розділити. Помістіть десяткову крапку в частку над десятковою крапкою в дивіденді.
    4. Напишіть частку відповідним знаком.
    Вправа\(\PageIndex{28}\)

    Розділити:\(−25.65\div (−0.06)\).

    Відповідь

    Пам'ятайте, що ви можете «перемістити» десяткові числа в дільнику та дивіденді через властивість еквівалентних дробів.

      \(−25.65\div (−0.06)\)
    Прикмети ті ж. Коефіцієнт позитивний.
    Зробіть дільник цілим числом, «перемістивши» десяткову крапку вправо.  
    «Перемістити» десяткову крапку в дивіденд на таку ж кількість знаків. .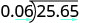
    Розділити.
    Помістіть десяткову крапку в частку над десятковою крапкою в дивіденді.    		 .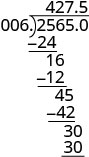
    Напишіть частку відповідним знаком. \(−25.65\div (−0.06) = 427.5\)
    Вправа\(\PageIndex{29}\)

    Розділити:\(−23.492\div (−0.04)\).

    Відповідь

    687.3

    Вправа\(\PageIndex{30}\)

    Розділити:\(−4.11\div(−0.12)\).

    Відповідь

    34.25

    Поширене застосування поділу цілих чисел на десяткові числа - це коли ми хочемо знайти ціну одного предмета, який продається як частина мульти-упаковки. Наприклад, припустимо, що випадок з 24 пляшками з водою коштує\($3.99\). Щоб знайти ціну однієї пляшки з водою, ми розділимо\($3.99\) на 24. Ми показуємо цей поділ у Вправі\(\PageIndex{31}\). У розрахунках з грошима округляємо відповідь до найближчого цента (сотого).

    Вправа\(\PageIndex{31}\)

    Розділити:\($3.99\div 24\).

    Відповідь
    Наведено .99 розділений на 24. Завдання довгого поділу встановлюється з 24 діленням 3.99. Наводиться таблиця з вказівками зліва і математичними кроками праворуч. Перший крок говорить: «Поставте десяткову крапку в частку над десятковою крапкою в дивіденді. Ділимо як зазвичай. Коли ми зупинимося? Так як цей поділ передбачає гроші, округляємо їх до найближчого цента (сотого). Для цього ми повинні віднести поділ на тисячне місце». Праворуч від цього, у нас є довга проблема поділу, встановлена з 24 діленням 3.990. Коефіцієнт задається як 0.166. Щоб показати роботу, нижче 3.990 він читає 24, суцільна горизонтальна лінія, 159, 144, суцільна горизонтальна лінія, 150, 144, суцільна горизонтальна лінія, і, нарешті, 6. П'ятий крок говорить «Округлити до найближчого цента». Праворуч від цього, ми маємо $0.166 приблизно дорівнює $0.17 і, отже, >.99 ділиться на 24 $0.17». >
      \($3.99\div 24\)
    Помістіть десяткову крапку в частку над десятковою крапкою в дивіденді.  
    Ділимо як зазвичай.
    Коли ми зупиняємося? Так як це поділ передбачає гроші, округляємо їх до найближчого цента (сотих.) Для цього треба віднести поділ на тисячне місце.    		 .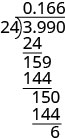
    Округлити до найближчого цента. \($0.166\approx $0.17\)
    \($3.99\div 2\approx $0.17\)
    Вправа\(\PageIndex{32}\)

    Розділити:\($6.99\div 36\).

    Відповідь

    \($0.19\)

    Вправа\(\PageIndex{33}\)

    Розділити:\($4.99\div 12\).

    Відповідь

    \($0.42\)

    Перетворення десяткових дробів, дробів та відсотків

    Переводимо десяткові дроби в дроби, позначивши місце останньої (найдальшої правої) цифри. У десятковому 0.03 3 знаходиться на сотому місці, тому 100 - знаменник дробу, еквівалентний 0,03.

    \[00.03 = \frac { 3 } { 100 }\]

    Зверніть увагу, коли число зліва від десяткового числа дорівнює нулю, ми отримуємо дріб, чисельник якого менше його знаменника. Дроби, подібні до цього, називаються правильними дробами.

    Кроки, які потрібно зробити для перетворення десяткового дробу, підсумовуються у вікні процедури.

    ПЕРЕТВОРЕННЯ ДЕСЯТКОВОГО ДРОБУ В ПРАВИЛЬНИЙ ДРІБ.
    1. Визначте місце значення кінцевої цифри.
    2. Запишіть дріб.
      • чисельник — «числа» праворуч від десяткової крапки
      • знаменник — значення місця, відповідне кінцевій цифрі
    Вправа\(\PageIndex{34}\)

    Запишіть 0.374 як дріб.

    Відповідь
      0,374
    Визначте місце значення кінцевої цифри. .

    Напишіть дріб для 0.374:

    • Чисельник - 374.
    • Знаменник - 1000.
    		 \(\dfrac{374}{1000}\)
    Спростити дріб. \(\dfrac{2\cdot 187}{2\cdot 500}\)
    Розділіть загальні фактори. \(\dfrac{187}{500}\)
    Отже,\(0.374=\dfrac{187}{500}\)

    Ви помітили, що кількість нулів у знаменнику\(\dfrac{374}{1000}\) збігається з кількістю десяткових знаків у 0,374?

    Вправа\(\PageIndex{35}\)

    Запишіть 0.234 як дріб.

    Відповідь

    \(\dfrac{117}{500}\)

    Вправа\(\PageIndex{36}\)

    Запишіть 0.024 як дріб.

    Відповідь

    \(\dfrac{3}{125}\)

    Ми навчилися перетворювати десяткові числа в дроби. Тепер ми зробимо зворотне - перетворить дробові дроби в десяткові. Пам'ятайте, що брусок дробу означає поділ. Так\(\dfrac{4}{5}\) може бути написано\(4\div 5\) або\(5)\overline{4}\). Це призводить до наступного методу перетворення дробу в десятковий.

    ПЕРЕТВОРЕННЯ ДРОБУ В ДЕСЯТКОВИЙ.

    Щоб перетворити дріб в десятковий, розділіть чисельник дробу на знаменник дробу.

    Вправа\(\PageIndex{37}\)

    Запишіть\(-\dfrac{5}{8}\) як десяткове число.

    Відповідь

    Оскільки дробний бар означає поділ, ми починаємо з написання\(\dfrac{5}{8}\) як\(8)\overline{5}\). Тепер ділимо.

    Це довга задача ділення з 8 діленням 5.000 і 0.625 як частка. Нижче 5.000 ми маємо 48, суцільна горизонтальна лінія, 20, 16, суцільна горизонтальна лінія, 40, і остаточна горизонтальна лінія. Таким чином, п'ять восьмих дорівнює 0,625.

    Вправа\(\PageIndex{38}\)

    Запишіть\(-\dfrac{7}{8}\) як десяткове число.

    Відповідь

    −0,875

    Вправа\(\PageIndex{39}\)

    Запишіть\(-\dfrac{3}{8}\) як десяткове число.

    Відповідь

    −0,375

    Коли ми ділимо, ми не завжди отримаємо нульовий залишок. Іноді частка закінчується десятковою комою, яка повторюється. Повторювана десяткова - це десяткова кома, в якій остання цифра або група цифр повторюється нескінченно. Смуга розміщується над повторюваним блоком цифр, щоб вказати, що він повторюється.

    ПОВТОРЮВАНІ ДЕСЯТКОВІ

    Повторювана десяткова - це десяткова кома, в якій остання цифра або група цифр повторюється нескінченно.

    Смуга розміщується над повторюваним блоком цифр, щоб вказати, що він повторюється.

    Вправа\(\PageIndex{40}\)

    Запишіть\(\dfrac{43}{22}\) як десяткове число.

    Відповідь

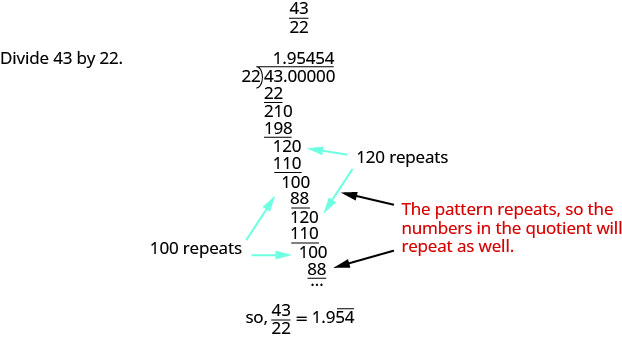
    Наведено число 43/22. Напрямок віддано на «Розділити 43 на 22». Дано довгу задачу ділення з 22 діленням 43.00000 з часткою 1.95454. Нижче 43.00000 ми маємо 22, суцільна горизонтальна лінія, 210, 198, суцільна горизонтальна лінія, 120, 110, горизонтальна лінія, 100, 88, суцільна горизонтальна лінія, 120, 110, суцільна горизонтальна лінія, 100, 88, суцільна горизонтальна лінія, а потім три точки. Зазначається, що 120 повторюється і що 100 повторюється. Це далі експлуатується як «Візерунок повторюється, тому числа в частці повторюватимуться також. В кінці нам дається твердження, що 43/22 дорівнює 1,954 з невеликою горизонтальною лінією над 54.

    Вправа\(\PageIndex{41}\)

    Запишіть\(\dfrac{27}{11}\) як десяткове число.

    Відповідь

    \(2.\overline{45}\)

    Вправа\(\PageIndex{42}\)

    Запишіть\(\dfrac{51}{22}\) як десяткове число.

    Відповідь

    \(2.3\overline{18}\)

    Іноді нам, можливо, доведеться спростити вирази з дробами та десятковими числами разом.

    Вправа\(\PageIndex{43}\)

    Спростити:\(\dfrac{7}{8}+6.4\).

    Відповідь

    Спочатку ми повинні змінити одне число, щоб обидва числа були в одній формі. Ми можемо змінити дріб на десятковий, або змінити десятковий на дріб. Зазвичай простіше змінити дріб на десятковий.

        \(\dfrac{7}{8}+6.4\)
    \(\dfrac{7}{8}\)Змінити на десяткову. .  
    Додати.   \(0.875+6.4\)
        \(7.275\)
        Отже,\(\dfrac{7}{8}+6.4 = 7.275\)
    Вправа\(\PageIndex{44}\)

    Спростити:\(\dfrac{3}{8}+4.9\).

    Відповідь

    \(5.275\)

    Вправа\(\PageIndex{45}\)

    Спростити:\(5.7 + \dfrac{13}{20}\).

    Відповідь

    \(6.35\)

    Відсоток - це коефіцієнт, знаменник якого дорівнює 100. Відсоток означає на сто. Ми використовуємо символ відсотка,%, щоб показати відсоток.

    ВІДСОТОК

    Відсоток - це коефіцієнт, знаменник якого дорівнює 100.

    Оскільки відсоток - це співвідношення, його легко можна виразити у вигляді дробу. Відсоток означає на 100, тому знаменник дробу дорівнює 100. Потім ми міняємо дріб на десятковий, діливши чисельник на знаменник.

    \[\begin{array} {llll} {} &{\text{6%}} &{\text{78%}} &{\text{135%}} \\ {\text { Write as a ratio with denominator } 100. } &{\dfrac{6}{100}} &{\dfrac{78}{100}} &{\dfrac{135}{100}} \\ { \text { Change the fraction to a decimal by dividing}} &{0.06} &{0.78} &{1.35}\\ {\text{the numerator by the denominator.}} &{} &{} &{} \end{array}\]

    Ви бачите візерунок? Щоб перетворити процентне число в десяткове число, переміщаємо десяткову крапку на два розряди вліво.

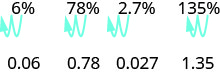
    Перша частина цього малюнка показує 6% зі стрілкою, проведеною між 6 та знаком відсотка до простору ліворуч від 6, а потім до простору далі ліворуч від цього простору. Нижче наведено число 0,06. Друга частина цього малюнка показує 78% зі стрілкою, проведеною між 8 і знак відсотка до простору між 7 і 8, а потім до простору зліва від 7. Нижче наведено число 0,78. Третя частина цього малюнка показує 2,7% зі стрілкою, проведеною від десяткової крапки до пробілу ліворуч від 2, а потім до простору далі ліворуч від цього простору. Нижче наведено число 0.027. Четверта частина цього малюнка показує 135% зі стрілкою, проведеною між 5 та знаком відсотка до простору між 3 і 5, а потім до простору між 1 і 3. Нижче наведено число 1.35.
    Малюнок\(\PageIndex{2}\)
    Вправа\(\PageIndex{46}\)

    Перетворіть кожен відсоток у десятковий:

    1. 62%
    2. 135%
    3. 35,7%.
    Відповідь
    1.  
      .
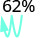
    Перемістіть десяткову крапку на два розряди вліво. 0,62
    2.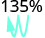  
      .
    Перемістіть десяткову крапку на два розряди вліво. 1.35
    3.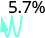  
      .
    Перемістіть десяткову крапку на два розряди вліво. 0,057
    Вправа\(\PageIndex{47}\)

    Перетворіть кожен відсоток у десятковий:

    1. 9%
    2. 87%
    3. 3,9%.
    Відповідь
    1. 0,09
    2. 0,87
    3. 0.039
    Вправа\(\PageIndex{48}\)

    Перетворіть кожен відсоток у десятковий:

    1. 3%
    2. 91%
    3. 8,3%.
    Відповідь
    1. 0,03
    2. 0.91
    3. 0.083

    Перетворення десяткового числа в відсоток має сенс, якщо ми пам'ятаємо визначення відсотків і маємо на увазі значення місця.

    Щоб перетворити десяткове число в відсоток, пам'ятайте, що відсоток означає на сто. Якщо ми змінимо десятковий дріб, знаменник якого дорівнює 100, легко змінити цей дріб на відсоток.

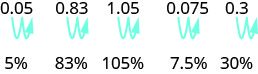
    \[\begin{array} {llll} {} &{0.83} &{1.05} &{0.075} \\ {\text {Write as a fraction }} &{\frac{83}{100}} &{\small{1}\frac{5}{100}} &{\frac{75}{1000}} \\ { \text {The denominator is 100.}} &{} &{\frac{105}{100}} &{\frac{7.5}{100}}\\ {\text{Write the ratio as a percent.}} &{\text{83%}} &{\text{105%}} &{\text{7.5%}} \end{array}\]

    Розпізнати закономірність? Щоб перетворити десяткове число в відсоток, ми переміщаємо десяткову крапку на два розряди вправо, а потім додаємо знак відсотка.

    Перша частина цього малюнка показує 0,05 зі стрілкою, проведеною від десяткової крапки до пробілу між 0 і 5, а потім до пробілу після 5. Нижче наведено число 5%. Друга частина цього малюнка показує 0,83 зі стрілкою, проведеною від десяткової крапки до пробілу між 8 і 3, а потім до пробілу після 3. Нижче наведено число 83%. Третя частина цього малюнка показує 1,05 зі стрілкою, проведеною від десяткової крапки до пробілу між 0 і 5, а потім до пробілу після 5. Нижче наведено число 105%. Четверта частина цього малюнка показує 0,075 зі стрілкою, проведеною від десяткової крапки до пробілу між 0 і 7, а потім до пробілу між 7 і 5. Нижче наведено число 7,5%. П'ята частина цього малюнка показує 0,3 зі стрілкою, проведеною від десяткової крапки до пробілу після 3, а потім пробіл далі праворуч від цього 3. Нижче наведено число 30%.
    Малюнок\(\PageIndex{3}\)
    Вправа\(\PageIndex{49}\)

    Перетворіть кожне десяткове число у відсотки:

    1. 0,51
    2. 1,25
    3. 0.093.
    Відповідь
    1.  
      .
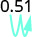
    Перемістіть десяткову крапку на два розряди вправо. \(51%\)
    2.  
      .
    Перемістіть десяткову крапку на два розряди вправо. \(125%\)
    3.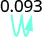  
      .
    Перемістіть десяткову крапку на два розряди вправо. \(9.3%\)
    Вправа\(\PageIndex{50}\)

    Перетворіть кожне десяткове число у відсотки:

    1. 0,17
    2. 1.75
    3. 0.0825
    Відповідь
    1. 17%
    2. 175%
    3. 8,25%
    Вправа\(\PageIndex{51}\)

    Перетворіть кожне десяткове число у відсотки:

    1. 0,41
    2. 2.25
    3. 0.0925.
    Відповідь
    1. 41%
    2. 25%
    3. 9,25%

    Ключові концепції

    • Назвіть десяткову
      1. Назвіть число ліворуч від десяткової крапки.
      2. Запишіть «і» для десяткової крапки.
      3. Назвіть частину «число» праворуч від десяткової крапки так, ніби це ціле число.
      4. Назвіть десятковий розряд останньої цифри.
    • Напишіть десяткову
      1. Шукайте слово «і» - воно знаходить десяткову крапку. Поставте десяткову крапку під словом «і». Перекладіть слова перед «і» в ціле число і помістіть його ліворуч від десяткової крапки. Якщо немає «і», напишіть «0» з десятковою крапкою праворуч.
      2. Відзначте потрібну кількість десяткових знаків праворуч від десяткової крапки, зазначивши значення місця, зазначене останнім словом.
      3. Переведіть слова після «і» в число праворуч від десяткової крапки. Запишіть число в пробілах - поставивши остаточну цифру на останнє місце.
      4. Заповніть нулі для власників місць у міру необхідності.
    • Округлити десяткову
      1. Знайдіть задане значення місця і позначте його стрілкою.
      2. Підкресліть цифру праворуч від значення місця.
      3. Ця цифра більше або дорівнює 5? Так — додайте 1 до цифри у вказаному значенні місця. Ні — не змінюйте цифру в заданому місці.
      4. Перепишіть число, видаливши всі цифри праворуч від округлення цифри.
    • Додавання або віднімання десяткових знаків
      1. Запишіть числа так, щоб десяткові крапки вибудовувалися вертикально.
      2. Використовуйте нулі в якості власників місця, якщо потрібно.
      3. Додайте або відніміть числа так, ніби вони цілі числа. Потім помістіть десяткову кому у відповіді під десятковими крапками в заданих числах.
    • Множення десяткових знаків
      1. Визначте ознаку вироби.
      2. Пишіть у вертикальному форматі, вишикуючи цифри праворуч. Помножте числа так, ніби вони цілі числа, тимчасово ігноруючи десяткові крапки.
      3. Розставте десяткову крапку. Число десяткових знаків у добутку - це сума десяткових знаків у множниках.
      4. Напишіть виріб відповідним знаком.
    • Помножте десяткове число на ступінь десяти
      1. Перемістіть десяткову крапку вправо на ту ж кількість знаків, що і кількість нулів в ступені 10.
      2. Додайте нулі в кінці числа за потребою.
    • Розділити десяткові числа
      1. Визначте ознаку частки.
      2. Зробіть дільник цілим числом, «перемістивши» десяткову крапку вправо. «Перемістіть» десяткову крапку в дивіденд на таку ж кількість знаків - додаючи нулі в міру необхідності.
      3. Розділити. Помістіть десяткову крапку в частку над десятковою крапкою в дивіденді.
      4. Напишіть частку відповідним знаком.
    • Перетворення десяткового дробу на правильний дріб
      1. Визначте місце значення кінцевої цифри.
      2. Запишіть дріб: чисельник — «числа» праворуч від десяткової крапки; знаменник — значення місця, відповідне кінцевій цифрі.
    • Перетворити дріб на десятковий Розділіть чисельник дробу на знаменник.