3.5: Алгоритми віднімання
- Page ID
- 66895
Вам знадобляться: Базові блоки (Матеріальні карти 4-15)
Найбільш поширеним алгоритмом віднімання є стандартний алгоритм віднімання справа наліво, де ви починаєте в стовпці одиниць і віднімаєте, потім переміщаєтеся вліво і віднімаєте в кожному стовпці. Проблема, звичайно, полягає в тому, коли верхня цифра менше нижньої цифри і доводиться перегрупувати. Отримайте свої блоки Base Ten зараз, щоб побачити, що насправді відбувається.
Розглянемо задачу віднімання 425 —158. З наших знань про значення місця ми знаємо, що 425 це 4\(\times\) 100 + 2\(\times\) 10 + 5 (або 400 + 20 + 5) і 158 - 1\(\times\) 100 + 5\(\times\) 10 + 8 (або 100 + 50 + 8). Використовуючи блоки Base Ten, 425 буде представлений з 4 квартирами, 2 лонгами та 5 одиницями, тоді як 158 будуть представлені 1 квартира, 5 лонгів та 8 одиниць. Отже, проблему віднімання можна придумати наступним чином:
Використання базових блоків\[\begin{aligned} (4 \text{ flat(s) } + 2 \text{ long(s) } + 5 \text{ unit(s) }) \\ \underline{– (1 \text{ flat(s) } + 5 \text{ long(s) } + 8 \text{ unit(s) })} \end{aligned} \nonumber \]
Використовуючи блоки, задача віднімання показана нижче:
Ми не можемо відняти 8 одиниць з 5 одиниць, тому довгий обмінюється на десять одиниць, що дає 4 квартири, 1 довгий і 15 одиниць в minuend. Тепер ми також не можемо відняти 5 лонгів з 1 довгого, тому 1 квартира обмінюється на десять лонгів, що дає 3 квартири, 11 лонгів і 15 одиниць в minuend. Тепер ми можемо відняти кожен стовпець, який показаний на наступній сторінці. Для віднімання можна використовувати підхід «забрати» або «відсутні доповнення». Використовуйте свої базові блоки для роботи з цими проблемами.
Використання базових блоків\[\begin{aligned} &(3 \text{ flat(s) } + 11 \text{ long(s) } + 15 \text{ unit(s)}) \\ -& (1 \text{ flat(s) } + 5 \text{ long(s) } + 8 \text{ unit(s)}) \\ \hdashline &2 \text{ flat(s) } + 6 \text{ long(s) } + 7 \text{ unit(s)}) = \underline{267} \end{aligned} \nonumber \]
Задача віднімання з використанням блоків показана нижче:
Оскільки ми працюємо в Base Ten, відповідь (різниця) дорівнює 267. Так, 425 —158 = 267.
Проблему можна працювати за допомогою діаграми, де залишається достатньо місця між мінуендом та відніманням, щоб обміни могли бути зроблені в minuend. Зверніть увагу на кроки, показані, якщо ви працюєте з цією проблемою за допомогою базової діаграми, як показано нижче.
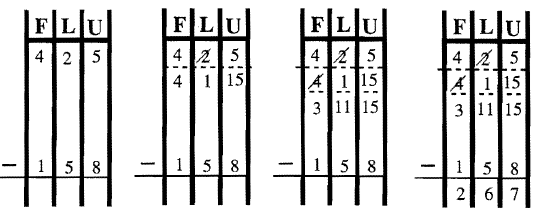
Тепер ми виконаємо цей базовий алгоритм в різних базах. Зверніть увагу на підставу при відніманні! Наприклад, у першому прикладі нижче ви повинні обміняти флет на ще 9 лонгів (оскільки це Base Nine). Один із способів показати це насправді додати 9 (база) до кількості лонгів вже там, так що я перекреслити 5, і додати 9, щоб отримати 14. Якщо ви пишете його таким чином, пам'ятайте, що номер, який ви пишете, знаходиться в базовій десятці, а не в базі, в якій ви працюєте. Написати його таким чином, мабуть, найпростіше, коли ви вперше починаєте віднімати. Більш елегантний спосіб - написати його так само, як ви працюєте в базовій десятці, тобто поставивши 1 перед 5 у стовпці лонгів, так що це виглядає як 15 (це не означає п'ятнадцять), що в Base Nine представляє 14 лонгів (5 лонг+9 більше від біржі)! Показані обидва способи її написання. Можливо, ви захочете використовувати свої базові блоки, щоб допомогти візуалізувати фактичні обміни, що здійснюються. Вивчіть наступні приклади. Перевірте кожну відповідь, додавши відповідь до відніманого і подивіться, що ви отримаєте minuend!
| \(\begin{aligned} 253_{\text{nine}} \\ \underline{-182_{\text{nine}}} \end{aligned}\) |
| \(\begin{aligned} 3\text{E}1_{\text{twelve}} \\ \underline{-14\text{T}_{\text{twelve}}} \end{aligned}\) |
| \(\begin{aligned} 402_{\text{five}} \\ \underline{-233_{\text{five}}} \end{aligned}\) |
| \(\begin{aligned} 1010_{\text{two}} \\ \underline{-111_{\text{two}}} \end{aligned}\) |
Перевірка:\(\begin{aligned} 11_{\text{two}} \\ \underline{+111_{\text{two}}} \\ 1010_{\text{two}} \end{aligned}\)
У прикладах 3 і 4, коли мені потрібно було зробити обмін, і ліворуч був нуль, обмін повинен був бути зроблений на більш високому місці значення спочатку. Потім обміни робляться вниз по рядку, поки ви не зможете відняти. Цей випадок відбувається в базовій десятці весь час, коли ви віднімаєте число від 100, 1000, 10000 тощо Більшість людей просто починають перетинати кожен нуль і ставити 9 вище за ними за звичкою, не маючи уявлення, чому вони це роблять. Щоб відняти 235 з 1000, спочатку слід перекреслити 1, поставити над ним нуль і поставити 1 перед нулем на місці ста (яка торгується в 1000 за 10 сотень), потім слід перекреслити те 10 на місці сотні, поставити над ним 9 і поставити 1 перед нулем на місці десятка (який обмінюється 10 сотень на 9 сотень і 10 десятків), потім слід перекреслити, що 10, поставити 9 над ним і 1 перед нулем на своєму місці (який обмінює 10 десятків на 9 десятків і 10 одиниць). Потім ви можете відняти, як показано в прикладі праворуч. Важливо дійсно розуміти, що тут відбувається, тому що дітям зазвичай дуже важко, коли є нуль, щоб перекреслити.
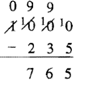
Виконайте наступні завдання віднімання. Ви можете використовувати блоки або діаграми, щоб допомогти візуалізувати проблему, але врешті-решт ви хочете працювати над тим, щоб мати можливість робити їх без маніпуляцій. Під кожною задачею перевірте, додавши різницю (відповідь) до віднімання (число віднімається) і перевірте, чи є сума minuend (число зверху). Використовуйте будь-який алгоритм додавання, який ви віддаєте перевагу.
| а.\(\begin{aligned} 4 5 2_{\text{thirteen}} \\ \underline{-1 3 \text{E}_{\text{thirteen}}} \end{aligned}\) | б.\(\begin{aligned} 8 3 1_{\text{nine}} \\ \underline{-6 7 0_{\text{nine}}} \end{aligned}\) | c.\(\begin{aligned} 2 0 0 4_{\text{six}} \\ \underline{-3 3 5_{\text{six}}} \end{aligned}\) | д.\(\begin{aligned} 4 2 1_{\text{five}} \\ \underline{-2 3 2_{\text{five}}} \end{aligned}\) | е.\(\begin{aligned} 1 0 0_{\text{three}} \\ \underline{-1 1_{\text{three}}} \end{aligned}\) |
Перевірте кожну проблему тут:
| а. | б. | c. | д. | е. |
Традиційний, стандартний алгоритм віднімання не обов'язково найкращий, і є багато інших, які ви будете вивчати в решті частини цього набору вправ.
Наступний алгоритм був навчений багатьом людям перед «новою математикою», і тому я називаю його алгоритмом Олдтаймера. Це схоже на Стандартний алгоритм тим, що ви починаєте праворуч і рухаєтеся вліво. Але ви не перегрупувати (формально відомий як запозичення). Спочатку подивіться ще раз на приклад використання Стандартного алгоритму для віднімання 95 — 28. Оскільки ви не можете відняти 8 з 5, ви перегрупуєте з 9, перекреслюючи 9 та написавши 8, щоб ви могли поставити 1 перед 2. Тепер в колонці одиниці 15 — 8 = 7, а в десятці - 8 — 2 = 6. Відповідь - 67. Цей новий метод починається так само. Ви не можете відняти 8 з 5, але замість того, щоб перегрупувати з 9, ви додаєте 1 до числа під 9, і ставите 1 перед 5. Зверніть увагу, що в стовпці одиниці, 15 - 8 = 7, а в стовпці десяти, замість 8 —2, у вас є 9 —3, що є тією ж відповіддю 6. Перевага цього методу полягає в тому, якщо ви ставите 1 у верхній частині одного стовпця, ви компенсуєте додаванням 1 в нижній частині наступного стовпця. Вам не доведеться турбуватися про перетин речей і зробити безлад, і вам не доведеться думати про цифру в стовпці зліва, поки ви не перейдете до цього стовпця, щоб відняти - не намагайтеся перегрупувати і зациклюватися там! Подивіться на два способи пліч-о-пліч. Якщо ви використовуєте новий метод, вам доведеться залишати простір між рядком віднімання та віднімання, якщо вам потрібно поставити там 1.
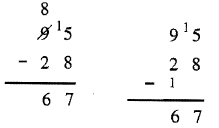
Що мені дуже подобається в методі Олдтаймера, так це те, що його набагато простіше перевірити. Просто складіть кожен стовпець. Немає перенесення: 7 + 8 = 15 і 6 + 1 + 2 = 9. Це вітерець. Щоб перевірити стандартний алгоритм, ну це щось на зразок безладу, і вам потрібно буде записати його де-небудь ще і перевірити його. Вивчіть наступні приклади.
Вам все одно доведеться бути дуже обережним, щоб приділити пильну увагу підставі. Коли ви ставите 1 перед цифрою, пам'ятайте, що вона позначає число, яке є основою. Ще один спосіб вказати те ж саме - виписати, що це означає, як показано нижче. Ті ж п'ять прикладів проілюстровані знову, роблячи це таким чином. Це не так елегантно, але якщо це допомагає їхати додому те, що насправді відбувається, зробіть це так.
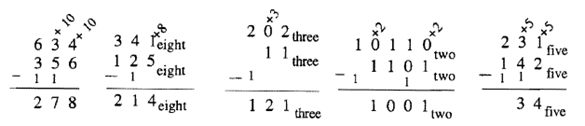
Відніміть наступне за допомогою алгоритму Олдтаймера. Перевірте свої відповіді, склавши.
| а.\(\begin{aligned} 5 0 3 6 \\ \underline{-3 4 1 8} \end{aligned}\) | б.\(\begin{aligned} 314_{\text{four}} \\ \underline{-221_{\text{four}}} \end{aligned}\) | c.\(\begin{aligned} 5 \text{T} 2_{\text{twelve}} \\ \underline{-2 3 \text{E}_{\text{twelve}}} \end{aligned}\) | д.\(\begin{aligned} 4 1 3_{\text{six}} \\ \underline{-3 2 4_{\text{six}}} \end{aligned}\) | е.\(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-1 0 1_{\text{two}}} \end{aligned}\) |
| ф.\(\begin{aligned} 537_{\text{nine}} \\ \underline{-273_{\text{nine}}} \end{aligned}\) | г.\(\begin{aligned} 312_{\text{five}} \\ \underline{-224_{\text{five}}} \end{aligned}\) | ч.\(\begin{aligned} 502_{\text{seven}} \\ \underline{-235_{\text{seven}}} \end{aligned}\) | я.\(\begin{aligned} 200_{\text{three}} \\ \underline{-121_{\text{three}}} \end{aligned}\) | Дж.\(\begin{aligned} 523_{\text{eight}} \\ \underline{-265_{\text{eight}}} \end{aligned}\) |
Тепер, коли ви освоїли цей алгоритм, ось ще один для вас. Це алгоритм зліва направо, де не відбувається перегрупування до кінця проблеми - ви перегрупуєте з відповіді! Ось як це працює. Почніть з крайнього лівого стовпчика і відніміть. Перейти до наступного стовпця. Відніміть, якщо це можливо. Якщо вам потрібно перегрупувати, поставте 1 перед верхньою цифрою, як зазвичай, і поставте косу риску через попередню цифру у відповіді. Ви заберете від відповіді врешті-решт. Перейдіть до наступного стовпця, поки не закінчите стовпчик пристрою. Потім поверніться назад і відніміть одну з усіх цифр зі слешем через них. Вивчіть наступний приклад, який показаний крок за кроком.
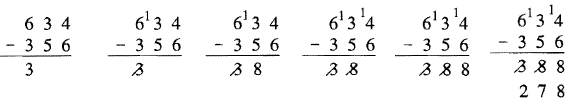
Ось кілька прикладів в інших базах. Якщо ви віддаєте перевагу, замість того, щоб ставити 1 перед цифрою під час перегрупування, ви можете поставити, наприклад, +4, якщо це в базовій четвірці, як це було показано для попереднього алгоритму внизу останньої сторінки.
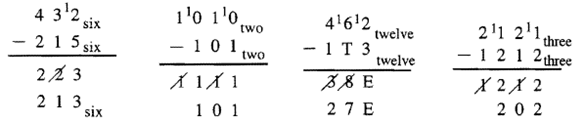
Перевірте наведені вище приклади, виконавши наступні проблеми додавання.
| \(\begin{aligned} 213_{\text{six}} \\ \underline{+215_{\text{six}}} \end{aligned}\) | \(\begin{aligned} 101_{\text{two}} \\ \underline{+101_{\text{two}}} \end{aligned}\) | \(\begin{aligned} 2 7 \text{E}_{\text{twelve}} \\ \underline{+1 \text{T} 3_{\text{twelve}}} \end{aligned}\) | \(\begin{aligned} 202_{\text{three}} \\ \underline{+1212_{\text{three}}} \end{aligned}\) |
Відніміть наступне за допомогою алгоритму зліва направо..
| а.\(\begin{aligned} 8 0 4 2 \\ \underline{-1 3 2 5} \end{aligned}\) | б.\(\begin{aligned} 4132_{\text{five}} \\ \underline{-2413_{\text{five}}} \end{aligned}\) | c.\(\begin{aligned} 7210_{\text{eight}} \\ \underline{-5564_{\text{eight}}} \end{aligned}\) | д.\(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{-569_{\text{thirteen}}} \end{aligned}\) | е.\(\begin{aligned} 1 1 0 1_{\text{two}} \\ \underline{-1 1_{\text{two}}} \end{aligned}\) |
Перевірте відповіді на вправу 4, виконавши відповідну проблему додавання
У цьому алгоритмі є ще одна маленька деталь. Якщо ви закреслюєте нуль, необхідно продовжити перекреслення цифри зліва від нуля. Якщо в рядку більше одного нуля, коли ви йдете вліво, перехрестіть кожен нуль, поки не дійдете до ненульової цифри. Потім відніміть 1 з кожного перекресленого числа, як і раніше. Зверніть увагу на базу: У другому прикладі нижче число перед 40five дорівнює 34five. У третьому прикладі число перед 100two дорівнює 11два. Вивчіть наступні приклади.
Відніміть наступне за допомогою алгоритму зліва направо.
| а.\(\begin{aligned} 8 0 4 2 \\ \underline{-1 3 4 5} \end{aligned}\) | б.\(\begin{aligned} 4132_{\text{five}} \\ \underline{-2433_{\text{five}}} \end{aligned}\) | c.\(\begin{aligned} 7210_{\text{eight}} \\ \underline{-5214_{\text{eight}}} \end{aligned}\) | д.\(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{-539_{\text{thirteen}}} \end{aligned}\) | е.\(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-10 1_{\text{two}}} \end{aligned}\) |
Перевірте відповіді на вправу 6, виконавши відповідну проблему додавання.
Алгебра допоможе розібратися в наступному алгоритмі:
М — S = М — S + х — х = М + х — S — х = (М + х) — (S + х)
М — S = М — S + х — х = М — х — S + х = (М —х) — (S — х)
В основному, це говорить про те, що для віднімання двох чисел, M (minuend) і S (віднімання), ви отримаєте ту ж відповідь, якщо спочатку додати (або відняти) одне і те ж число до обох M і S перед відніманням. Алгоритм Олдтаймера працює через цей факт. Наприклад, коли ви ставите 1 перед цифрою одиниці minuend і 1 нижче десятизначної цифри віднімання, ви додаєте як 10 до minuend, так і до віднімання; потім, ви віднімаєте.
Цей алгоритм особливо корисний, якщо minuend має рядок нулів в кінці. Відніміть 1 з мінуенда і спочатку відніміть, а потім виконайте віднімання. Подивіться, як це працює:
| \(\begin{aligned} 100000 && && 99999 \\ \underline{–65378} && && \underline{–65377} \\ 34622 &&= && 34622 \end{aligned}\) | \(\begin{aligned} 3000 && && 2999\\ \underline{–1264} && && \underline{–1263} \\ 1736 && = && 1736 \end{aligned}\) |
Ну, як ви думаєте? Чи не друге віднімання, показане в кожній парі, простіше зробити, ніж перше? Я тільки що віднімала 1 з minend і віднімала спочатку!
Складіть дві власні проблеми віднімання, використовуючи цей метод для віднімання.
Цей алгоритм також добре працює, якщо віднімання близьке до ступеня основи, як 100, 1000 тощо Наприклад, для задачі віднімання 4503 — 997 додайте 3 до мінуенду та відніміть так, щоб задача стала 4506 — 1000 = 3506. У задачі Base Four\(2302_{\text{four}} – 333_{\text{four}}\) додайте 1 до обох, щоб отримати\(2303_{\text{four}} – 1000_{\text{four}} = 1303_{\text{four}}\)
Складіть дві власні проблеми віднімання, використовуючи цей метод для віднімання. Використовуйте базу, відмінну від 10.
Вищевказаний метод іноді називають комплементарним методом. Існує ще більш конкретний підхід, який називається комплементарним алгоритмом. Він спирається на ідею доповнень, які ми визначили в більш ранньому наборі вправ. У базовій десятці, пари доповнень були 1 & 9, 2 & 8, 3 & 7, 4 & 6 і 5 & 5. Для комплементарного методу ви знайдете дуже специфічне доповнення віднімання та додаєте його як до мінуенду, так і до віднімання перед відніманням. Доповнення, в даному випадку, є 1, за яким слідують лише нулі, такі, що кількість нулів - це однакова кількість цифр у минуенді. По-перше, вам доведеться придумати простий спосіб знайти доповнення заданого числа.
Нижче наведено приклади, що показують, як знайти доповнення (C) заданого числа (A), якщо ви хочете, щоб A + C складалося до числа B.
А = 74 і В = 1000.
Рішення
Щоб знайти C, додайте 6 до 74, щоб отримати 80, потім 20, щоб отримати 100 і 900, щоб отримати 1000. С = 926.
А =\(24_{\text{six}}\) і В =\(1000_{\text{six}}\).
Рішення
Щоб знайти C, додайте 2 одиниці, щоб отримати 3 лонги, потім 3 лонги, щоб отримати 1 квартиру і 5 квартир, щоб отримати 1 блок. Тоді C =\(532_{\text{six}}\).
Існують і інші способи з'ясувати доповнення. Наприклад, у базовій десятці, якщо A дорівнює 28403, і ви хочете C такий, що A + C = 1000000, ви можете знайти відповідь, написавши фактичне доповнення 3, що дорівнює 7, для цифри одиниці. Рухайтеся вліво. Ви хочете, щоб цифра для кожного місця значення, що при додаванні до цифри там дає суму 9. Робіть це до тих пір, поки число не матиме стільки цифр, скільки нулів в 1000000. У цьому випадку відповідь - 971597. Складніше пояснити, ніж робити! Якщо у вас є свій власний спосіб з'ясувати доповнення, це здорово! Не тримайте це в секреті.
Знайти доповнення (C) заданого числа (A) таке, що A + C = B.
а. а = 538 і Б = 10000
б. а =\(212_{\text{four}}\) і В =\(1000_{\text{four}}\)
с. а =\(1011_{\text{two}}\) і В =\(10000_{\text{two}}\)
Ось як працює цей взаємодоповнюючий метод. Розглянемо задачу 452 — 74. Нам потрібно знайти число, яке при додаванні до 74 дорівнює 1000. Як вибрати, до чого він повинен скласти, як у 1000? Якщо перше число (minuend) є 2-значним числівником, ви хочете 1 з 2 нулями (100). Якщо перше число (minuend) є 3-значним числівником, ви хочете 1 з 3 нулями (1000) і так далі. Цей крок однаковий у всіх підставах. Повернутися до проблеми: 452 — 74:926 - це те, що потрібно додати до 74, щоб отримати 1000 (з прикладу 1). Додайте 926 до мінуенду та відніміть, щоб отримати нову задачу віднімання, яка є: 1378 - 1000 = 378. Відповідь - новий минуенд без першої цифри: 378. Досить дикий! Подивіться на\(402_{\text{six}} –24_{\text{six}}\). Нам потрібно знайти число, яке при додаванні до\(24_{\text{six}}\) є\(1000_{\text{six}}\)., яке\(532_{\text{six}}\) з Прикладу 2. Додайте\(532_{\text{six}}\) до minuend і відніміть, щоб отримати нову проблему віднімання, яка є\(1304 – 1000_{\text{six}} = 304_{\text{six}}\). Знову ж таки, відповідь - новий мінуенд без першої цифри:\(304_{\text{six}}\). Так ось хитрість - Просто додайте доповнення до minuend, зніміть першу цифру, і це відповідь! Віднімання немає.
Відніміть за допомогою комплементарного методу: 912 — 573
Рішення
427 - це число, яке при додаванні до 573 дорівнює 1000. Додаємо до мінусу: 427 + 912 = 1339. Знімаємо першу цифру і відповідь 339.
Відніміть\(301_{\text{four}} – 212_{\text{four}}\) за допомогою комплементарного алгоритму.
Рішення
З 10.b., доповнення є\(122_{\text{four}}\). \(301_{\text{four}} + 122_{\text{four}} = 1023_{\text{four}}\).
Отже, відповідь є\(23_{\text{four}}\).
Відніміть\(1100_{\text{two}} – 1011_{\text{two}}\) за допомогою комплементарного алгоритму і вашу відповідь з 10.c.
Виконайте наступні завдання віднімання за допомогою комплементарного методу.
| а.\(\begin{aligned} 5034 \\ \underline{–357} \end{aligned}\) | б.\(\begin{aligned} 420_{\text{five}} \\ \underline{–231_{\text{five}}} \end{aligned}\) |
Додатковий метод насправді простіше зробити з блоками - як тільки ви отримаєте повісити його. Вийміть свої блоки Base Three, щоб зробити наступний приклад і проблеми.
Для обчислення\(212_{\text{three}} – 120_{\text{three}}\) представляють\(212_{\text{three}}\) і\(120_{\text{three}}\) з блоками, як показано нижче.
Мінуенд показаний зліва. Оскільки його найбільшим «блоком» є квартира, наступний «місце значення» вгору блок. Отже, проблема полягає в тому, щоб з'ясувати, що потрібно додати до віднімання (показано праворуч), щоб зробити блок. Це було б 1 довший і 1 більш плоский. Іншими словами, якщо ви додали довгий і плоский до віднімання, у вас буде блок, чи не так? Додайте таку ж кількість до мінуенду, показаного зліва вище. Виглядати він повинен наступним чином:
Якщо відняти зараз, відповідь буде новий minuend з найбільшим блоком видалено. Тому відповідь - 2 лонга і 2 одиниці, або\(22_{\text{three}}\) Найважливішим кроком є з'ясування того, що потрібно додати до віднімання, щоб зробити блок. Потім, також додайте його до minuend, видаліть найбільший блок з нового minuend, і це відповідь! Та да!
Оскільки малювання блоків іноді громіздко, ще один спосіб наочно показати, що відбувається, - це використовувати скорочені зображення для базових трьох блоків, квартир, лонгів та одиниць (3B, 3F, 3L, U), як показано нижче.
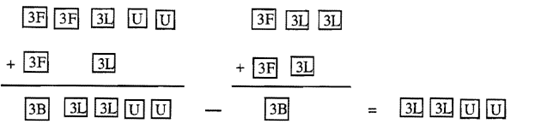
На наступній сторінці використовуйте відповідні базові блоки для віднімання\(120_{\text{three}} - 12_{\text{three}}\) та\(213_{\text{four}} - 133_{\text{four}}\) використання комплементарного методу. Поясніть, як це зробити, і покажіть повні або скорочені картинки з базовими блоками.
a Використовуйте базові три блоки та додатковий метод для віднімання\(120_{\text{three}} – 12_{\text{three}}\).
б Використовуйте базові чотири блоки та додатковий метод для віднімання\(213_{\text{four}} – 133_{\text{four}}\).
Поясніть, як кожен студент робить завдання віднімання 634 — 152.
a Мері робить віднімання в голові, думаючи вголос «534, 484, 482". Що таке її міркування?
б Педро робить віднімання, думаючи вголос «634 і 48 682, відняти 200 - 482». Що таке його міркування?
Інший метод віднімання називається Віднімання з базового алгоритму. Цей особливо приємний для роботи в інших базах. При цьому методі ніколи не потрібно віднімати з числа більше підстави.
Стандартний алгоритм:
| \(\begin{aligned} 534 \\ \underline{-256} \end{aligned}\)робити біржі\(\begin{aligned} {}^{4}&& {}^{12} &&{}^{14} \\ \cancel{5} &&\cancel{3}&&4 \\ -2&&5&&6 \\ \hline 2&&7&&8 \end{aligned}\) |
Використовуючи метод Відняти від Base, якщо у вас є місце, де нижнє число більше верхнього числа, перегрупуйте, як у традиційному методі, потім відніміть нижнє число від основи та додайте результат до верхнього числа. Перевага цього методу полягає в тому, що ви ніколи не віднімаєте число з будь-якого числа, більшого за основу. Це хороший метод для людей, яким потрібно використовувати пальці для віднімання.
Віднімаємо з базового алгоритму:
При використанні цього методу в інших основах обведіть базове число при перегрупуванні. Наприклад, при роботі в базовій шести, 6 не існує, і написання 10 може бути заплутаним, навіть якщо це правильно.
Відніміть наступне за допомогою алгоритму Віднімання з базового алгоритму. Це ті ж проблеми з #6. Не забудьте обвести базове число при перегрупуванні.
| а.\(\begin{aligned} 8 0 4 2 \\ \underline{-1345} \end{aligned}\) | б.\(\begin{aligned} 4 1 3 2_{\text{five}} \\ \underline{-2433_{\text{five}} } \end{aligned}\) | c.\(\begin{aligned} 7 2 1 0_{\text{eight}} \\ \underline{ -5214_{\text{eight}}} \end{aligned}\) | д.\(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{ -539_{\text{thirteen}}} \end{aligned}\) | е.\(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-101_{\text{two}} } \end{aligned}\) |
Чи знаєте ви інший алгоритм додавання або віднімання? Якщо так, опублікуйте його з поясненням на форумі для додаткового кредиту.
