3.4: Віднімання
- Page ID
- 66906
Вам знадобиться: Калькулятор, Базові блоки (Матеріальні картки 4-15) C-Strips (Матеріальні картки 16A-16L)
Як би ви використовували маніпулятив, щоб пояснити, як робити віднімання маленькій дитині?
Існує два різних підходи до віднімання. Один з нас знайомий з методом Take-Away. Типовим способом хтось може представити ідею віднімання, кажучи: «Якщо я поклав п'ять яблук в миску, а потім забираю два яблука, скільки залишилося в мисці?» На малюнку нижче показано це як проблему віднімання, коли після того, як два яблука виймаються з миски, залишається три яблука.
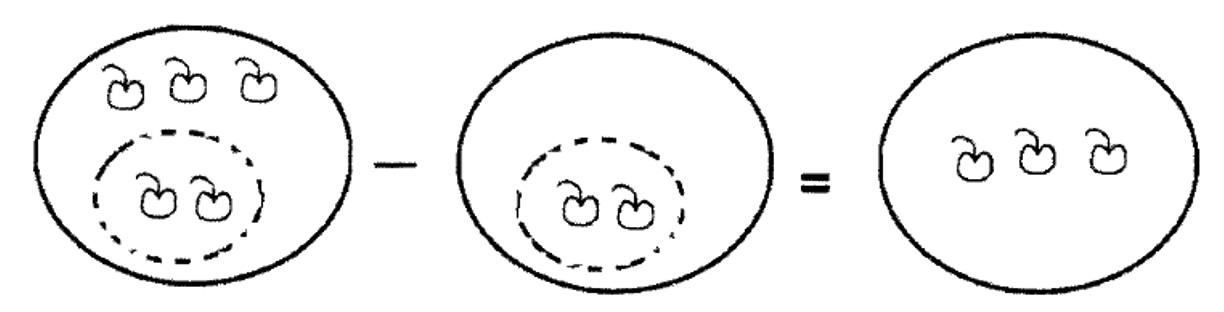
Наведена вище проблема ілюструє підхід до віднімання.
Словник віднімання: Для x — y = z, x називається минуендом, y називається відніманням, а z (відповідь) називається різницею.
Для задачі віднімання 7 — 3 вкажіть
Якщо B є підмножиною A, то n (A) — n (B) = n (A — B)
Своїми словами поясніть, як використовувати визначення віднімання. Які кроки беруть участь?
Приклади того, як зробити віднімання за допомогою визначення теорії множин:
Використовуйте визначення теорії множин віднімання, щоб показати, що 5 - 2 = 3.
Нехай A = {v, w, x, y, z} і B = {w, z}. Оскільки n (А) = 5, n (B) = 2 і В\(\subseteq\) А,
\[\begin{aligned} 5 – 2 &= n(A) – n(B) && \text{ by substituting } n(A) \text{ for 5 and } n(B) \text{ for 2} \\ &= n(A – B) && \text{ by the set theory definition of subtraction} \\ &= n(\{v,x,y\}) && \text{ by computing }A – B \\ &= 3 && \text{ by counting the elements in } A – B \end{aligned} \nonumber \]
Тому 5 — 2 = 3.
Використовуйте визначення теорії множин віднімання, щоб показати, що 6 - 1 = 5.
Нехай A {1, 2, 3, 4, 5, 6} і B = {4}. Оскільки n (А) = 6, n (B) = 1 і B\(\subseteq\) A,
\[\begin{aligned} 6 – 1 &= n(A) – n(B) && \text{ by substituting } n(A) \text{ for 6 and } n(B) \text{ for 1} \\ &= n(A – B) && \text{ by the set theory definition of subtraction} \\ &= n(\{1, 2, \mathbf{3}, 5, 6\}) && \text{ by computing }A – B \\ &= 5 && \text{ by counting the elements in } A – B \end{aligned} \nonumber \]
Тому 6— 1 = 5.
Використовуйте визначення теорії множин віднімання, щоб показати, що 3 — 0 = 3.
Нехай A = {x, y, z} і B = {}. Оскільки n (A) =3, n (B) =0 і B\(\subseteq\) A,
\[\begin{aligned} 3 – 0 &= n(A) – n(B) && \text{ by substituting } n(A) \text{ for 3 and } n(B) \text{ for 0} \\ &= n(A – B) && \text{ by the set theory definition of subtraction} \\ &= n(\{x,y,z\}) && \text{ by computing }A – B \\ &= 3 && \text{ by counting the elements in } A – B \end{aligned} \nonumber \]
Тому 3 — 0 = 3.
Для кожної задачі віднімання нижче надайте два множини, які дозволяють використовувати визначення віднімання для пошуку відповіді. Потім обчислити відповідь, використовуючи це визначення.
- 7 - 3
- 6 - 0
- 4 - 4
Частини b і c вправи 4 ілюструють дві знайомі властивості віднімання.
Перша властивість стверджує, що для будь-якого цілого числа\(m\),\(m – 0 = m\). Використовуючи наші знання з теорії множин, виберіть перший набір A, який має m елементів, а потім виберіть другий набір B, який має нульові елементи - є лише один набір, який ви можете вибрати, і це нульовий або порожній набір, {}. Тоді A — {} = А. Отже, це факт, що m — 0 = 0.
Друга властивість стверджує, що для будь-якого цілого числа m, m — m = 0. Це має бути істинним, тому що для будь-якої множини A, будь то m елементів або будь-яка інша кількість елементів, ми знаємо з теорії множин, що A — A = {}.
Ми будемо використовувати підхід Take-Away для виконання завдань віднімання в Єгипті зараз.
Вам нагадують символи та їх індуї-арабські еквіваленти нижче:
| | (1) |
 (10) |
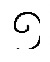 (100) |
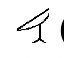 (1 000) |
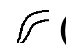 (10 000) |
 (100 000) |
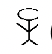 (1 000 000) |
Щоб використовувати підхід Take-Away, ми хочемо бачити віднімання як підмножину minuend, а потім видалити віднімання з minuend. Символи, які залишаються в minuend є різниця. У цьому першому прикладі зверніть увагу на те, як виконується наступне віднімання. У цьому випадку ви можете бачити віднімання як підмножини minuend. Навколо того, що потрібно забрати, ставиться коробка, і остаточна відповідь зрозуміла.
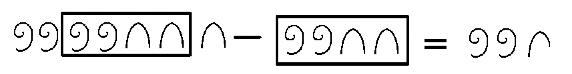
Іноді обмін доводиться робити в minuend, перш ніж можна буде зробити віднімання. Наприклад, розглянемо наступне віднімання:
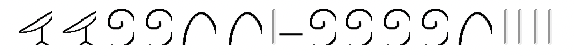
Першим кроком було б зробити деякі обміни в minuend. Одну квітку лотоса потрібно обміняти на десять сувоїв і одну п'яткову кістку обміняти на десять штабів. Після цього віднімання можна виконати, як показано нижче:
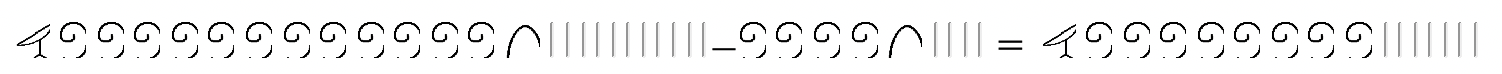
У наведеному вище прикладі поставте поле навколо підмножини, яка видаляється з minuend.
Наступним відніманням буде
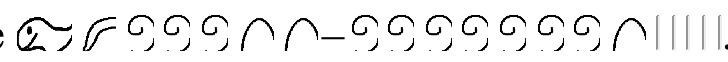
. Цього разу віднімання буде показано у вигляді вертикальної задачі з мінуендом та відніманням, показаними у вікні. Для того, щоб зробити віднімання, спочатку загострений палець в мінуенді потрібно обміняти на десять квіток лотоса. Потім одну квітку лотоса потрібно обміняти на десять сувоїв і одну п'яткову кістку обміняти на десять ударів. Нарешті, підмножина (віднімається) забирається з мінуенда. Я простежував, що видаляється. Символи, що залишилися в minuend, є відповіддю (
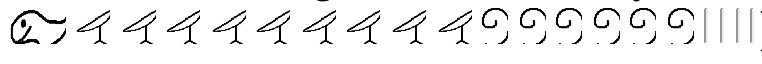
), як показано на ілюстрації нижче.
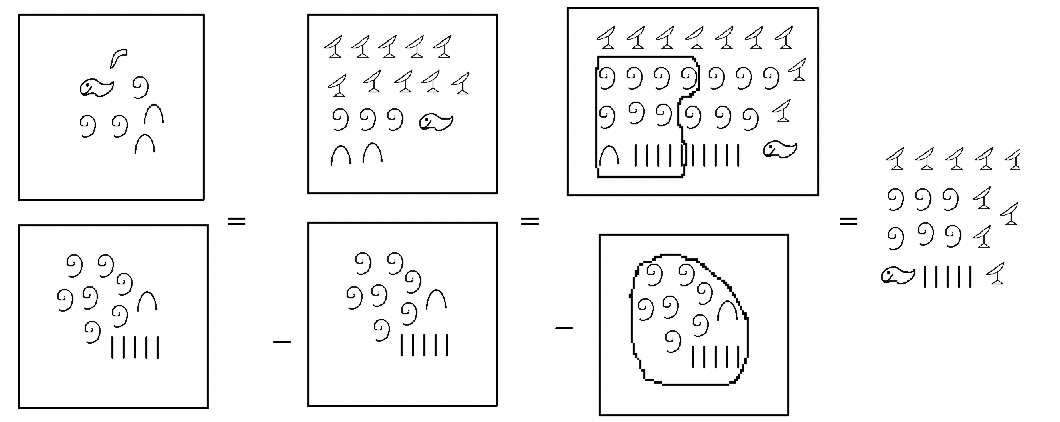
Виконайте наступні завдання віднімання в єгипетській мові, показуючи всі кроки. Ви можете моделювати проблему, як вам подобається, якщо кроки зрозумілі.
|
а. 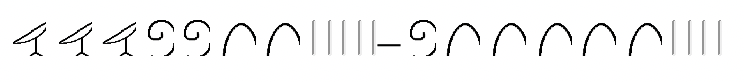 |
б.  |
Давайте використаємо підхід на винос, щоб відняти числівники майя. Це схоже на додавання в тому, що ви видаляєте підмножину на кожному рівні - біржі або торги, можливо, доведеться зробити, перш ніж мати можливість забрати на будь-якому рівні. Зверніть пильну увагу на те, на якому рівні ви перебуваєте при здійсненні обмінів. Крапку на одному рівні можна торгувати для групи з 20 на наступному рівні вниз, за винятком від третього рівня до другого рівня - одна точка на третьому рівні замінюється групою з 18 на другому рівні. Вивчіть наступні приклади. Подивіться, чи зможете ви з'ясувати, які біржі робляться. Я вкажу обміни, які здійснюються з одного рівня на інший стрілкою вниз.
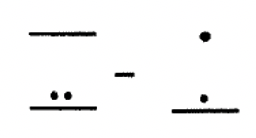
Рішення

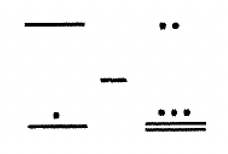
Рішення
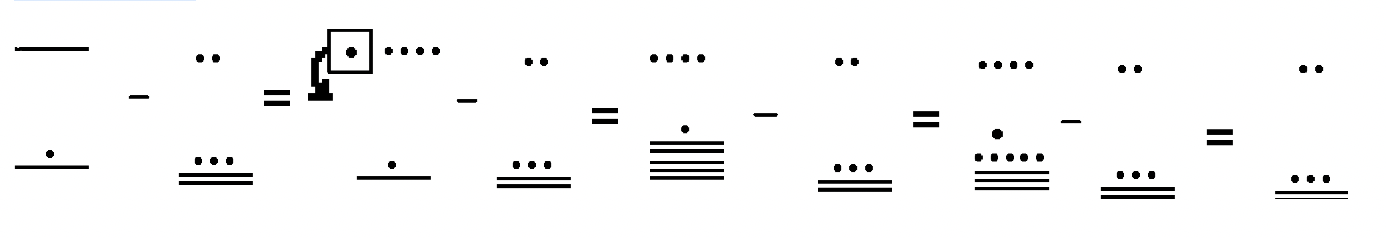
У прикладах 1 та 2 зауважте, що, оскільки обміни робляться в minuend (так що ви можете використовувати підхід на винос), віднімання просто продовжує повторюватися. По черзі, ви можете спочатку показати обмін, який робиться для minuend, зробити перерву (як пунктирну лінію, як показано нижче), а потім записати проблему віднімання та віднімання. Ось ще один спосіб, ви можете показати кроки для Прикладу 2.
Виконайте наступну проблему віднімання в майя і показати всі кроки.
Ось ще кілька прикладів.
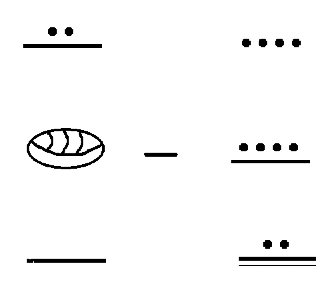
Рішення
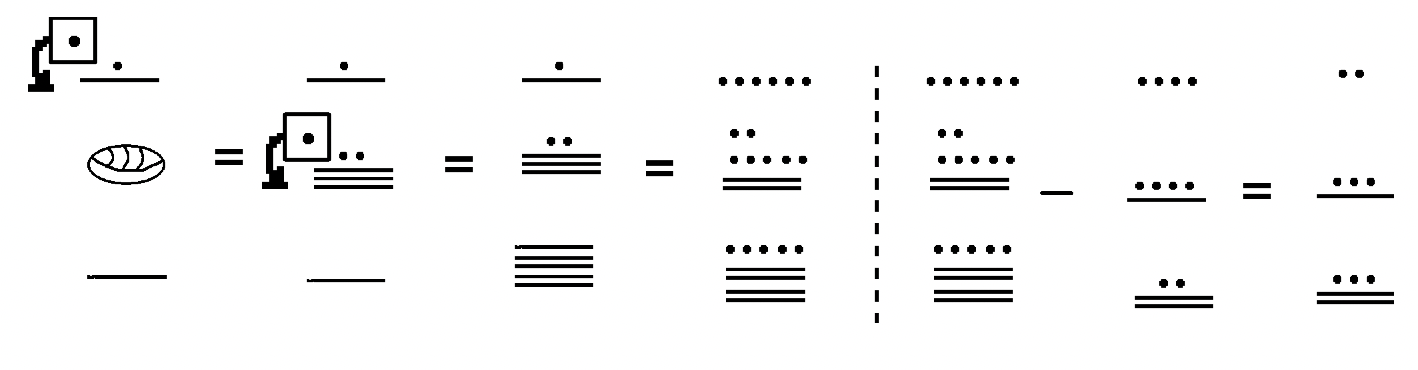
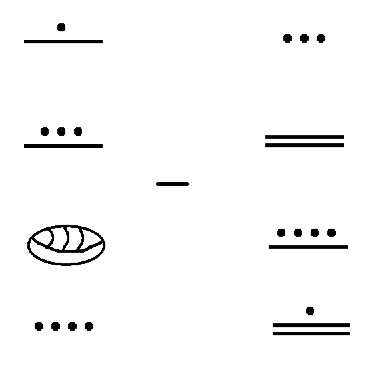
Рішення
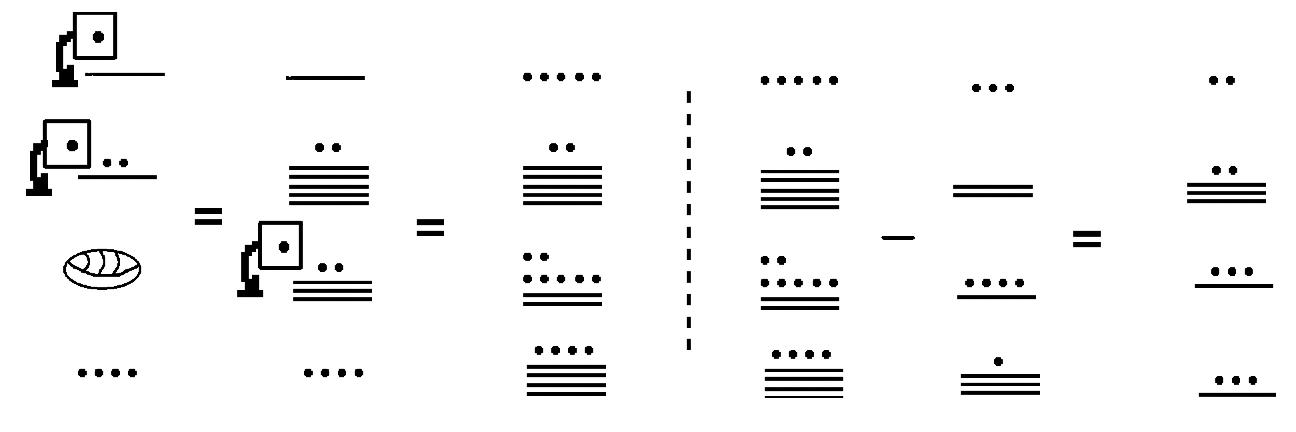
Потрібно багато концентрації та зусиль, щоб правильно працювати з ними. Виконуйте кожен крок обережно, тому що легко помилитися. Кожен з попередніх чотирьох прикладів можна перевірити, додавши відповідь до відніманого і побачивши, чи є сума мінуендом. Інший спосіб перевірити - перетворити minuend і subtrahend в індуї-арабську, відняти в індуї-арабській, а потім перетворити різницю в майя, переконавшись, що відповідь така ж, як і той, який ви придумали, коли ви зробили це в майя. Ось перевірка на прикладі 4:46,084 —25,396 = 20,688. Я зробив помилки з цієї проблеми в перший раз через, але знайшов свої помилки, перевіривши і почавши спочатку. Обов'язково слід перевірити свої відповіді. Спробуйте зробити приклади 3 і 4 вище самостійно, перш ніж перейти до наступної вправи.
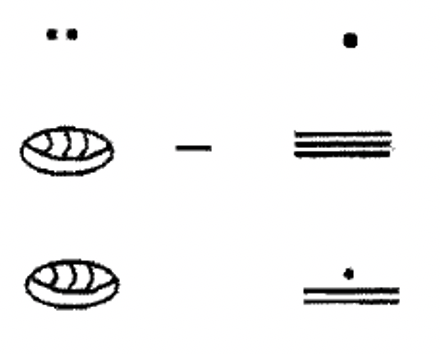
Виконайте наступні завдання віднімання в майя. Показати всі кроки і перевірити!
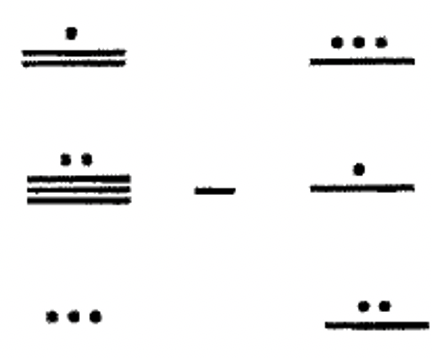 |
 |
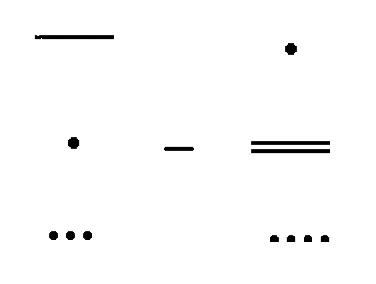 |
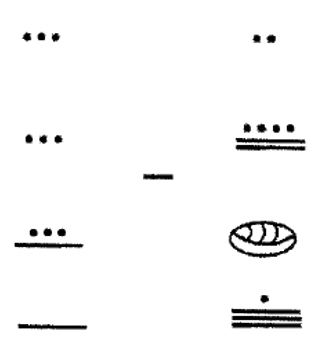 |
Виймаємо набір базових чотирьох блоків. Ми збираємося зробити проблему віднімання 17 - 7 в базовій четвірці. \(101_{\text{four}}\)є базовою четвіркою для 17 і\(13_{\text{four}}\) є базовою чотирма числівниками для 7. Ми зробимо купу, яка називається Pile A, використовуючи базові чотири блоки для представлення 17 та іншу купу, яка називається Pile B, для представлення 7. Ваші купи повинні виглядати приблизно так, як ви бачите праворуч.
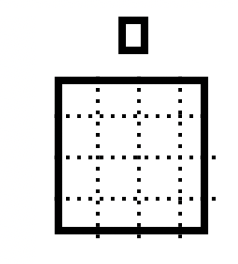 |
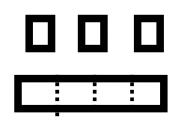 |
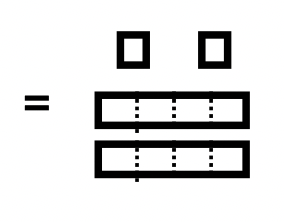
Нижче наведено ілюстрацію виконуваної задачі віднімання. Для того, щоб використовувати підхід на винос, купа B повинна бути підмножиною купи А. Ця точна підмножина повинна бути вилучена з купи А. По-перше, квартира в палі A повинна бути замінена на 3 лонги і 4 одиниці, щоб ви могли насправді побачити купу B всередині палі А. Є коробка навколо підмножини (купа B), яку потрібно видалити з купи А, зверніть увагу, як він відповідає Pile B. Після того, як забирають ці блоки, залишаються 2 лонги та 2 одиниці. Тому завершена задача віднімання є\(101_{\text{four}} – 13_{\text{four}} = 22_{\text{four}}\).
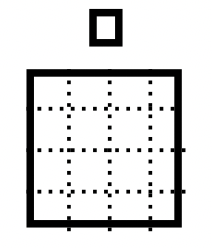 Купа А Купа А |
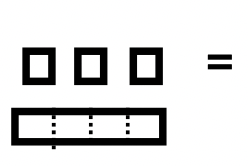 Ворс B Ворс B |
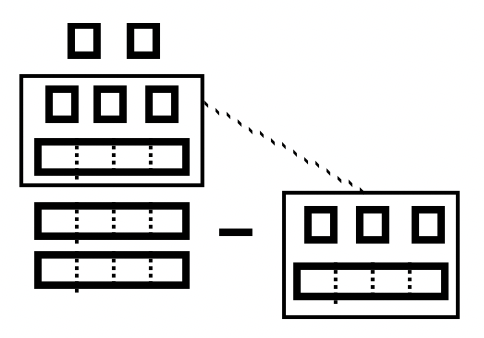 Ворс А - Ворс B Ворс А - Ворс B |
 |
Вийдіть і використовуйте базові блоки, щоб зробити наступні вправи! Дотримуйтесь вказівок.
Підрахуйте 17 одиничних блоків і зробіть обмін з базовими п'ятьма блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін в базовій п'ятірці, напишіть 17 як основу п'ять числівників на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 9 одиниць і зробіть обміни з базовими п'ятьма блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обміни в базовій п'ятій основі, напишіть 9 як основу п'ять числівників на просторі, передбаченому для купи B нижче. Якщо необхідно, зробіть обмін в купі A так, щоб точна підмножина купи B була помічена в купі А. Візьміть ті блоки в купі A, які представляють блоки в палі B. Блоки, залишені в палі A, є тими, які залишилися після віднімання блоків, які були в купі B. Якщо необхідно, зробити будь-які обміни з базовою п'ятьма блоки, а потім запишіть це число як основу п'ять числівників на третьому бланку, наданому нижче.
Нижче наведено проблему віднімання, яку ви щойно виконали в Base Five:
____________ + _____________ = _____________________
Паля A Купа B Різниця палі A і B
Перетворіть різницю (відповідь) на базову десятку. Вона повинна бути 8, так як 17 - 9 = 8. Це?
Проілюструйте проблему віднімання за допомогою блоків нижче. Покажіть кроки.
Підрахуйте 17 одиничних блоків і зробіть обмін з базовими вісьмома блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін в базовій вісім, напишіть 17 як базову вісім цифр на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 7 одиниць і зробіть обміни з базовими вісьмома блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обмін у вісім базових, напишіть 7 як базову вісім числівників на просторі, передбаченому для купи B нижче. Якщо необхідно, зробіть обмін в купі A так, щоб точна підмножина купи B була помічена в купі А. Візьміть ті блоки в купі A, які представляють блоки в палі B. Блоки, залишені в палі A, є тими, які залишилися після віднімання блоків, які були в купі B. Якщо необхідно, зробити будь-які обміни з базою. вісім блоків, а потім запишіть це число як основу вісім числівників на третьому бланку, наданому нижче.
Нижче наведено проблему віднімання, яку ви щойно виконали в Base Eight:
____________ + _____________ = _____________________
Паля A Купа B Різниця палі A і B
Перетворіть різницю (відповідь) на базову десятку. Вона повинна бути 10, так як 17 - 7 = 10. Це? Проілюструйте проблему віднімання за допомогою блоків нижче. Покажіть кроки.
Підрахуйте 21 блок блоків і зробіть обмін з базовими трьома блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін в основі три, напишіть 21 як основу три цифри на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 7 одиниць і зробіть обмін з базовими трьома блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обмін в основі три, напишіть 7 як основу три цифри на просторі, передбаченому для купи B нижче. Якщо необхідно, зробіть обмін в купі A так, щоб точна підмножина купи B була помічена в купі А. Візьміть ті блоки в купі A, які представляють блоки в палі B. Блоки, залишені в палі A, є тими, які залишилися після віднімання блоків, які були в купі B. Якщо необхідно, зробити будь-які обміни з базою. три блоки, а потім запишіть це число як основу три числівники на третьому бланку, наданому нижче.
Нижче наведено проблему віднімання, яку ви щойно виконали в Base Three:
Паля A Купа B Різниця палі A і B
Перетворіть різницю (відповідь) на базову десятку. Вона повинна бути 14, так як 21 —7 = 14. Це? Проілюструйте проблему віднімання за допомогою блоків нижче. Покажіть кроки.
Напишіть три завдання віднімання з вправ 8, 9 та 10 у вертикальному форматі, як у базовій четвірці (мій приклад), показаний праворуч. Вивчіть цю проблему Base Four, а також три проблеми, які ви записуєте. Спробуйте з'ясувати спосіб виконання завдань віднімання за допомогою паперу та олівця, а не за допомогою базових блоків. Іншими словами, спробуйте придумати власний алгоритм (метод) для виконання віднімання в інших базах. Поясніть свій метод і покажіть кілька прикладів. Пізніше ви будете вивчати алгоритми віднімання.
\[ \begin{aligned} 101_{\text{ four}} \\ \underline{ - 13_{\text{ four}}} \\ 22_{\text{ four}} \end{aligned} \nonumber \]
Використовуючи свої C-Strips, зробіть два поїзди, як зазначено. Нехай B + N буде першим поїздом\(t_{1}\), і нехай H + R буде другим поїздом,\(t_{2}\). Місце\(t_{1}\) примикає до t 2, як показано нижче. Знайдіть поїзд (запишіть його як єдину С-смужку), який при додаванні до t 2 сформує шлейф, рівний по довжині\(t_{1}\). Цей поїзд називається різницею двох поїздів,\(t_{1}\)\(t_{2}\) і позначається\(t_{1} –t_{2}\). Що таке\(t_{1} –t_{2}\)?

Використовуйте C-Strips, щоб знайти наступні відмінності. Намалюйте схему своєї роботи.
| а. Н — Л | б. S — D | c. Б — Ш |
| d. (Б + К) — N | е. (О + У) — П |
Використовуйте C-Strips для перевірки та ілюстрації кожного з наступних тверджень:
| а. (S + Y) — Y = S | б. (Н — Р) + Р = Н | в. (Б + Р) — Б = Р |
| d. Н — (Л+ Г) = Н — Л —Д | е. (Б + У) — (К + Л) = (В — К) + (У — Л) |
У вправі 12 для визначення різниці був використаний новий підхід. Існує два різних способи визначення віднімання - підхід на винос та підхід відсутніх додатків. Ми можемо використовувати модель для того, як різниця була визначена за допомогою поїздів і тепер застосувати її до визначення віднімання для цілих чисел. Нижче наведено визначення віднімання за допомогою моделі того, як різниця була визначена за допомогою поїздів у Вправі 12.
Визначення віднімання (підхід відсутніх додатків): Нехай a та b будуть будь-якими двома цілими числами. a — b - ціле число c таке, що a = b + c. Іншими словами, якщо до відніманого c додається, b, сума - минуенд, a. Відповідь, c, називається відсутнім додатком.
Чи існує відповідь на ціле число для кожної задачі віднімання цілого числа? Іншими словами, чи закрито віднімання цілих чисел? Поясніть свою відповідь і надайте контрприклад, якщо він не закритий.
Визначте, які множини, якщо такі є, закриті під віднімання. Наведіть контрприклад, якщо набір не закритий.
| а. {0} | б. {0, 2, 4, 6,...} |
Якщо ви думаєте про віднімання з точки зору відсутнього підходу додавання, то ми говоримо, що твердження a — b = c і a = b + c еквівалентні один одному. Розглянемо твердження, 8 — 2 = 6. Вона еквівалентна твердженню 8 = 2 + 6. Ми також знаємо, що 2 + 6 = 6 + 2 через комутативного властивості додавання. Тому 8 = 6 + 2, що в свою чергу еквівалентно твердженню 8 — 6 = 2. Це дає нам чотири факти про те, як зв'язати числа 2, 6 та 8 за допомогою додавання та віднімання.
| 8 — 2 = 6 |
| 8 = 2 + 6 |
| 8 — 6 = 2 |
| 8 = 6 + 2 |
Деякі вчителі пов'язують віднімання та додавання, використовуючи ідею «сімейства фактів», такі як чотири факти вище, що є одним фактом сім'ї.
Важливо зазначити, що кожне твердження додавання дає нам два твердження віднімання, саме стільки людей дізнаються свої факти віднімання. Через цей зв'язок між додаванням та відніманням, як тільки дитина дізнається основні факти додавання, природно слідують факти віднімання.
Запишіть два твердження віднімання, які еквівалентні кожному оператору додавання.
Ви можете здивуватися, чому я написав заяви про додавання у вправі 14 зі знаком плюс зліва від знака рівності, на відміну від того, як мені довелося написати два факти додавання в сімействі фактів, що стосуються 2, 6 і 8 у верхній частині сторінки. Це тому, що 8 + 4 = 12 - це той самий факт, що 12 = 8 + 4 через симетричну властивість рівності, яка визначена нижче.
Симетрична властивість рівності стверджує, що для будь-якого рівняння, якщо a = b, то також вірно, що b = a
Тому цілком нормально написати чотири факти вище як
| 2 + 6 = 8 |
| 6 + 2 = 8 |
| 8 — 2 = 6 |
| 8 — 6 = 2 |
Використовуйте симетричну властивість рівності, щоб переписати кожне рівняння.
| а. 7 — 3 = 4: _____ | б. 9 — 1 = 8: _____ |
Чи існує симетрична властивість нерівності? Поясніть.
Примітка: Нерівність відноситься до less than (<) and/or greater than (>).
Давайте зробимо проблему віднімання, використовуючи відсутній підхід доповнення в єгипетському. Налаштування точно така ж, як при використанні підходу на винос, але спосіб, яким ви йдете про пошук відповіді, відрізняється. Перший приклад, який ми розглянули в єгипетській мові, був
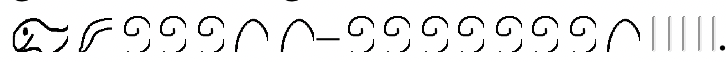
Ми запитуємо себе: «Що потрібно додати до
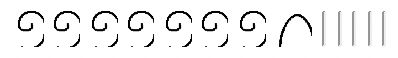
щоб отримати
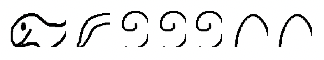
?» Ще один спосіб висловити це - написати:
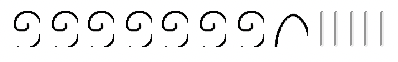
+?????? =
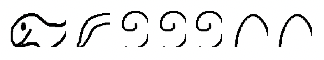
. Ми починаємо з перетворення в minuend, поки він не містить віднімання. Ми зробили ці точні кроки при використанні підходу на винос. Але щоб отримати остаточну відповідь, відзначимо, що потрібно додати до віднімання, щоб отримати мінуенд. Відповідь:

. Ілюстрація показана нижче.
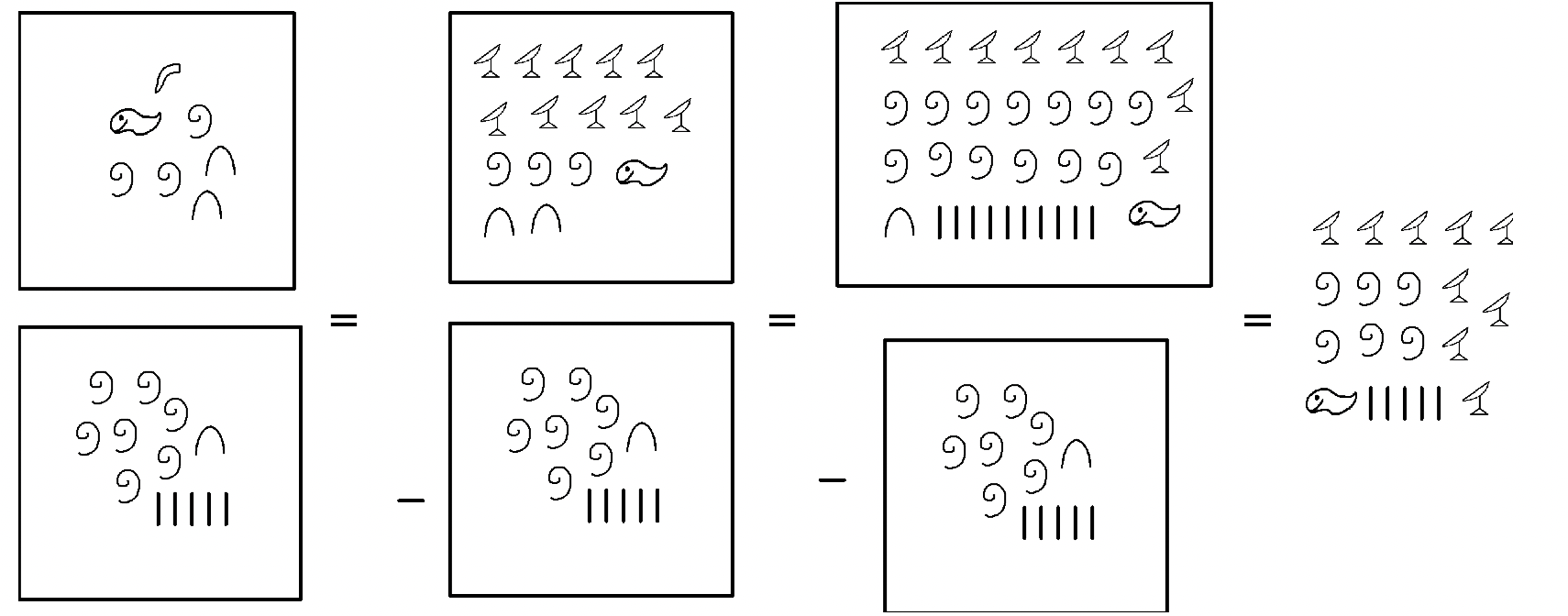
Щоб перевірити, чи відсутні доповнення (відповідь) + віднімається = минуенд. Іншими словами, чи вірно наступне твердження про додавання?
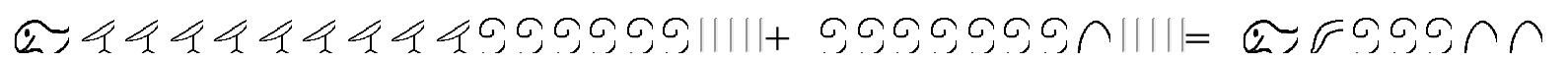
Ще один спосіб перевірки - перетворення на індуї-арабську мову.
Той самий підхід може бути використаний для віднімання в майя. Кроки, які використовуються для підготовки до пошуку відсутніх додатків, точно такі ж, як при використанні підходу на винос. Але щоб обчислити відповідь, на кожному рівні ви вирішуєте, які символи потрібно додати до віднімання, щоб отримати те, що знаходиться в мінуенді.
Хоча може бути важко розрізнити два підходи до віднімання, це спосіб, який ви думаєте про проблему, що робить її різною. Наприклад, одна дитина, яка дізнається про віднімання, може подумати про проблему 8 - 3, думаючи: «Якщо у мене 8 копійок в одній руці і забрати 3 з них, щоб покласти в кишеню, скільки залишилося в моїй руці?» Це підхід на винос. Дитина може обчислити відповідь, підраховуючи назад —7, 6, 5 або фактично використовуючи копійки або маніпуляції, де 8 копійки кладуть в одну руку, 3 забирають, а те, що залишилося, підраховується, щоб отримати відповідь. Інша дитина може подумати про ту саму проблему віднімання таким чином —"Якщо у мене є 3 копійки, скільки ще копійок мені потрібно, щоб у мене було 8 копійок?» Це відсутній підхід доповнення.
Складіть дві проблеми зі словами, які потребують обчислення завдання віднімання 8 - 3. Перший повинен використовувати підхід на винос, а другий - використовувати підхід відсутніх доповнень. Поясніть і покажіть, як би ви вирішували кожну проблему слова, використовуючи даний підхід.
| a. підхід на винос |
| б Відсутні доповнення Підхід |
Без використання маніпуляцій кожну задачу віднімання можна сформулювати як проблему додавання відсутніх додатків. Іншими словами, щоб знайти відповідь на 8 — 3, ви розбираєтеся, що йде в бланку на 3 + ____ = 8. Оскільки 3 + 5 = 8, то 8 - 3 = 5.
Виконайте наступні завдання віднімання, використовуючи підхід відсутніх доповнень. Заповніть пробіли
| а. 9 — 7 = ____ тому що _____________ |
| б. 13 — 6 = ____ тому що _____________ |
| c. 88 — 8 = ____ тому що ______________ |
| д. 70 — 14 = ____ тому що _____________ |
Використовуйте базові блоки для обчислення наступних задач віднімання, використовуючи підхід відсутніх додатків. Почніть з формування двох паль, один для мінуенда (Паля А) і один для віднімання (Паля B). Потім з'ясуйте, що повинно йти в третій купі (Купа X) так, щоб B + X = A. показати, як ви знайшли відповідь.
\(231_{\text{five}} – 140_{\text{five}}\)
\(100_{\text{two}} – 11_{\text{two}}\)
\(135_{\text{twelve}} – T6_{\text{twelve}}\)
Відсутній підхід доповнення іноді називають адитивним (або австрійським) алгоритмом.
Цей підхід дуже корисний для виконання віднімання на числовому рядку.
Розглянемо визначення віднімання з використанням підходу відсутніх доповнень. У ньому написано відповідь на a — b = c, де c - число, яке потрібно додати до b, щоб отримати c, або b + c = a.
Подумайте про це, використовуючи числовий рядок. Як би ми знайшли відповідь на 7 — 3? Нам потрібно знайти число, щоб додати до 3, що дає нам відповідь 7. Іншими словами, що б піти в порожньому 3 + ____ = 7? Я знаю, що ви знаєте відповідь, але як ми можемо отримати відповідь, використовуючи числовий рядок?
По-перше, ми повинні визначити новий термін: вектор. Вектор - це спрямований відрізок лінії. В основному спрямований вектор виглядає як стрілка. Вона має певну довжину і вказує в певному напрямку. Оскільки ми будемо використовувати горизонтальні числові лінії, ми будемо використовувати горизонтальні вектори. Стрілка, що вказує вправо, буде позначати позитивне число, а стрілка, що вказує вліво, - негативне число.
Нижче наведено числовий рядок з деякими векторами, показаними вище. Вектор a має довжину 6 одиниць і стрілка вказує вправо. Тому вона являє собою число +6. Вектор b також має довжину 6 одиниць, але він вказує ліворуч. Тому вона являє собою число -6.

а Яке число представляє вектор c? _________
б Яке число представляє вектор d? _________
Тепер ми готові використовувати вектори в поєднанні з відсутнім підходом додавання для обчислення завдання віднімання. Повернемося до проблеми 7 — 3. Відсутній підхід доповнення стверджує, що відповідь на проблему віднімання - це число, яке при додаванні до числа після знака віднімання дає число, яке знаходиться перед знаком віднімання. Оскільки 3 - це число після знака віднімання, ми повинні знайти число для додавання до 3, яке дасть відповідь 7. Використовуючи числовий рядок, це означає, що якщо ви починаєте з 3, як ви можете дістатися до 7? Іншими словами, намалюйте вектор, який починається з 3 і закінчується в 7. Переконайтеся, що стрілка вказує на 7. Число, яке представляє вектор, є відповіддю на задачу. Ілюстрація показана нижче. Вектор має довжину 4 і вказує праворуч, тому відповідь дорівнює 4, який написаний над вектором, щоб вказати відповідь.

Спробуємо проблему 2 - 9. Потім 9 + ____ = 2. На числовій лінії намалюйте вектор, який починається з 9 і закінчується на 2. Потім подивіться, яке число представляє вектор, щоб знайти відповідь. Вектор, показаний нижче, дає відповідь -7.
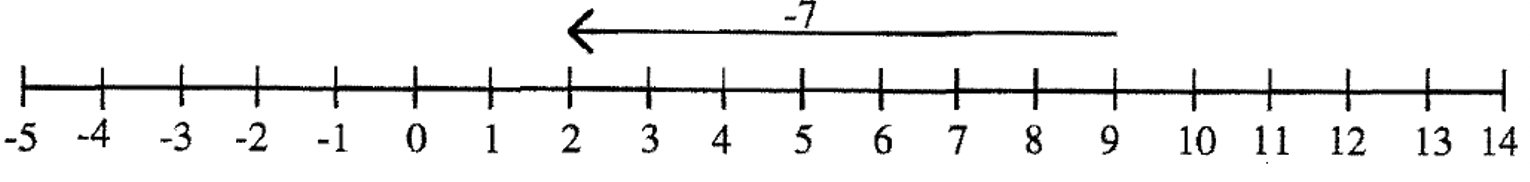
Знайти відповідь на наступні задачі віднімання можна за допомогою спрямованих векторів на числовому рядку у поєднанні з підходом відсутніх доповнень. Намалюйте вектори.
|
а. 10 - 4 = 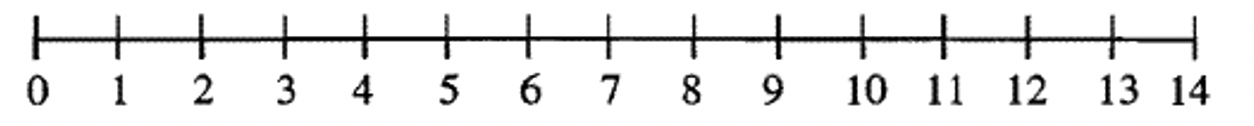 |
|
б. 12 - 5 = 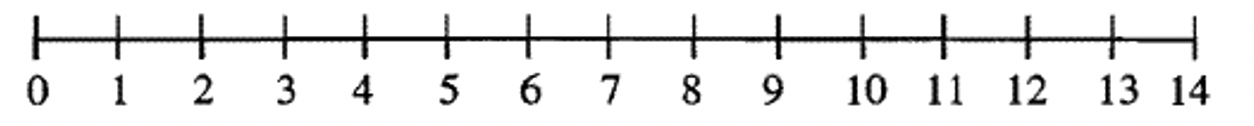 |
|
c. 8 - 3 = 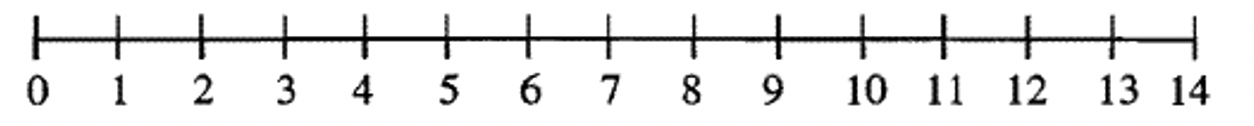 |
|
д. 9 - 7 = 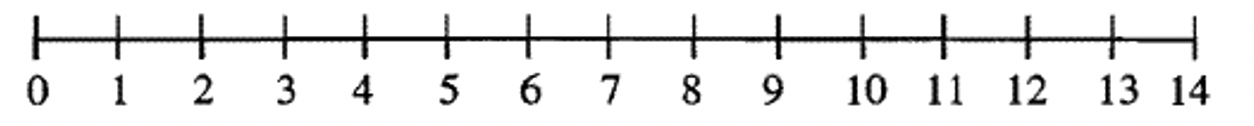 |
|
е. 3 - 10 = 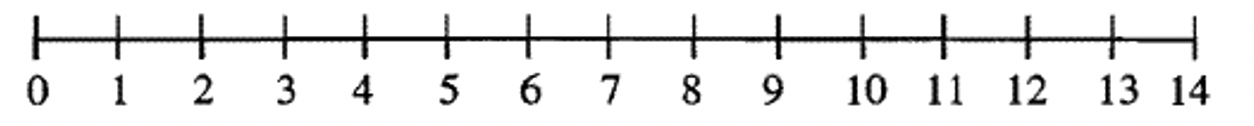 |
|
ф. 5 - 8 = 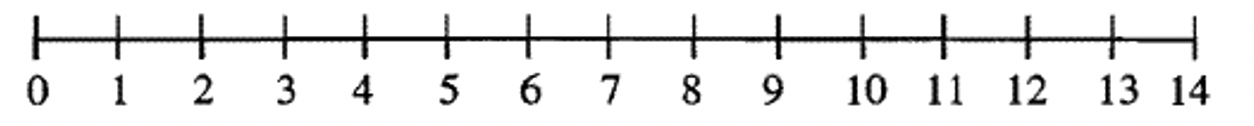 |
|
г. 1 - 13 = 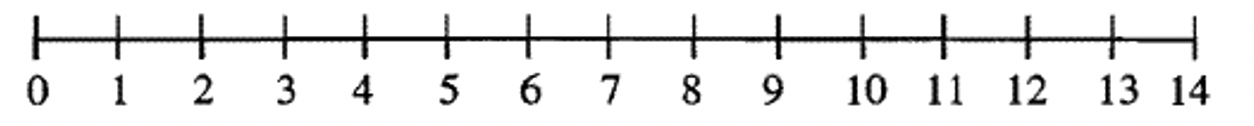 |
|
ч. 9 - 9 =  |
Дивлячись на вектори a — d нижче, з'ясуйте, яка задача віднімання виконувалася, а потім вкажіть відповідь. Наприклад, вектор b прийшов від виконання завдання -1 — 5. Отже, -1 — 5 = -6 (оскільки вектор b має довжину 6 одиниць і йде вліво).

| Вектор a: ____ | Вектор b: ____ | Вектор c: ____ |
