3.3: Алгоритми додавання
- Page ID
- 66890
Вам знадобляться: Калькулятор, Базові блоки (Матеріальні карти 4-15)
Немає жодного алгоритму, який кожен використовує для складання чисел разом. Викладач повинен бути знайомий з декількома методами, щоб можна було охопити найбільшу кількість учнів. Важливим є те, що студенти розуміють, що означає додавання, і вміють складати числа так чи інакше. Якщо студент з'ясовує алгоритм, який працює самостійно, я думаю, що це приголомшливо. Це показує творчість, і студент, ймовірно, не забуде його. Я сподіваюся, що все більше вчителів усвідомлюють, що багато шляхів можуть призвести до правильного вирішення проблеми, і що зазвичай немає підстав наполягати на тому, щоб студенти працювали над проблемою певним чином. Існує багато способів вирішення проблеми, і різноманітність слід заохочувати. Цей курс трохи відрізняється, тому що ви, мабуть, зацікавлені в тому, щоб стати викладачем. Тому для вас важливо навчитися якомога більше способів роботи з проблемами, а також виявити деякі власні методи. У цьому розділі ви будете вивчати різноманітні алгоритми додавання і повинні мати можливість опрацювати і пояснити процедури роботи проблеми за допомогою будь-якого з представлених методів. Ви дізнаєтеся деякі нові методи додавання і будете використовувати їх для додавання чисел в базовій десятці, а також в інших базах.
МЕТОД DOT для додавання стовпців однозначних цифр
Ось метод додавання декількох цифр разом без необхідності тримати велику загальну кількість у вашій голові. Ідея полягає в тому, що ви додаєте лише дві одиничні цифри одночасно. Кожного разу, коли ви додаєте та отримуєте число понад 9, ви ставите крапку і зберігаєте лише цифру пристрою у вашій пам'яті. Точка позначає десятку. Наприклад, оскільки 6 + 7 = 13 (це 10 + 3), ви пишете крапку і думаєте 3. Подумайте 6 + 7 = точка 3. У наведеному нижче прикладі, щоб додати вісім чисел разом, загальним підходом було б скласти перші дві цифри разом, а потім продовжувати додавати наступну цифру, поки не будуть додані всі вісім цифр. Іншими словами, хтось може подумати: 6 + 7 це 13, 13 + 8 - 21, 21 + 3 - 24, 24 + 5 - 29, 29 + 9 - 38, 38 + 4 - 42 і 42 + 7 - 49. Хоча це дає правильну відповідь, легко втратити слід на цьому шляху. При показаному DOT МЕТОДІ крапка ставиться числом, якщо після його додавання сума дорівнює десяти або більше. На кожному кроці шляху, Я написав в дужках, яке число ви думаєте про після додавання кожної цифри. Для початку дивіться вісім цифр, які потрібно додати. Крок 1:6 + 7 = 13 так напишіть крапку і подумайте 3; Крок 2:3 + 8 = 11 так напишіть крапку і подумайте 1; Крок 3:1 + 3 = 4 так подумайте 4; Крок 4:4 + 5 =9 так подумайте 9; Крок 5:9 + 9 = 18 так напишіть крапку і подумайте 8; Крок 6:8 + 4 = 12 так напишіть крапку і подумайте 2; Крок 7:2 + 7 = 9 так написати 9 під планкою, так як всі цифри мають додано. Підрахуйте точки (4), що позначає скільки десятків (40) і напишіть перед 9. Відповідь 49. Спробуйте це самостійно зараз!
| Старт\[ \begin{aligned} 6 \\ 7\\ 8 \\ 3 \\ 5\\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Крок 1\[ \begin{aligned} 6 \\ 7 &\cdot (3)\\ 8 \\ 3 \\ 5\\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Крок 2\[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot (1)\\ 3 \\ 5\\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Крок 3\[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 &\ (4) \\ 5\\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Крок 4\[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5 &\ (9) \\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Крок 5\[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5\\ 9 &\cdot (8) \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Крок 6\[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5\\ 9 &\cdot \\ 4 &\cdot (2)\\ \underline{+ 7} \end{aligned} \nonumber \] | Крок 7\[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5\\ 9 &\cdot \\ 4 &\cdot\\ + 7 &\ (9) \\ \hline 49 \end{aligned} \nonumber \] |
| \[ \begin{aligned} \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5\\ 9 &\cdot \\ 4 &\cdot\\ \underline{+ 7 } \\ 49 \end{aligned} \nonumber \] |
У прикладі, щойно показаному на попередній сторінці, відображається кожен крок, включаючи те, що ви думаєте. Насправді це швидкий алгоритм, і якщо ви подивилися на проблему після того, як хтось це зробив, робота зліва - це все, що ви б бачили. Праворуч наведено ще два приклади. Власне, кожна - це однакова сума чисел, написаних в різному порядку, що є ще одним способом перевірки додавання! Швидка перевірка при додаванні лише двох чисел полягає в тому, щоб змінити порядок і додати знову.
| \[ \begin{aligned} 3 \\ 9 &\cdot\\ 6 \\ 5 &\cdot\\ 4 \\ 7 &\cdot \\ 7 &\cdot\\ \underline{+ 8 } \\ 49 \end{aligned} \nonumber \] | \[ \begin{aligned} 6 \\ 3\\ 7 &\cdot\\ 9 &\cdot\\ 7 &\cdot \\ 5 \\ 8 &\cdot\\ \underline{+ 4 } \\ 49 \end{aligned} \nonumber \] |
Вправа 1
Використовуйте метод dot, щоб додати наступні стовпці цифр, показаних праворуч.
| \[ \begin{aligned} 3 \\ 9 \\4 \\5\\2\\6\\8\\6\\ \underline{+ 7} \end{aligned} \nonumber \] | \[ \begin{aligned} 6 \\ 7 \\ 9\\3\\5\\8\\2\\2\\ \underline{+ 9} \end{aligned} \nonumber \] | \[ \begin{aligned} 2\\9\\6\\4\\2\\5\\7\\9\\ \underline{+ 3} \end{aligned} \nonumber \] | \[ \begin{aligned} 5\\8\\7\\6\\3\\9\\2\\5\\ \underline{+ 7} \end{aligned} \nonumber \] |
До речі, ви могли б поставити крапки ліворуч або праворуч від цифри, робити все, що вам найбільш зручно. Якщо ви додаєте без паперу та олівця, використовуйте пальці, щоб відстежувати точки! Замість того, щоб писати крапку, поставте палець вгору. Принадність цього доповнення в тому, що вам ніколи не доведеться тримати в голові число вище дев'яти!
Точковий метод також може бути використаний для додавання декількох цифр, записаних у горизонтальному форматі. Крапки можуть бути розміщені над числівниками. Спробуйте його на наступних проблемах. Складіть власні проблеми для частини d і частини е.
| а. 7 + 6 + 4 + 5 + 9 + 6 + 8 + 3 + 4 + 9 + 8 = ____ |
| б. 4 + 9 + 6 + 2 + 9 + 7 + 7 + 6 + 8 + 4 + 8 = ____ |
| c. 7 + 9 + 8 + 5 + 9 + 4 + 2 + 6 + 9 + 8 + 7 = ____ |
| д. |
| е. |
Метод подряпин
Метод подряпин схожий на метод точки. Кожен раз, коли ви додаєте і отримуєте число більше дев'яти, ви подряпаєте останню додану цифру. Подряпина, як і точка, буде представляти десять. Так само, як і в точковому методі, ви зберігаєте лише цифру пристрою у вашій пам'яті або в якості альтернативи, запишіть цифру блоку праворуч і трохи нижче цифри просто подряпані. Це можна зробити і в точковому методі. Я проілюструю кроки, що беруть участь, записуючи цифри пристрою на цей раз. Коли сума менше десяти, вона тримається у вашій голові. Дужки будуть використані для позначення того, що я думаю в голові. Наступна проблема точно така ж, яку я робив раніше при використанні методу точки. Для початку дивіться вісім цифр, які потрібно додати. Крок 1:6 + 7 = 13 так подряпати 7 і написати 3; Крок 2:3 + 8 = 11 так подряпати 8 і написати 1; Крок 3:1 + 3 = 4 так думайте 4; Крок 4:4 + 5 =9 так подумайте 9; Крок 5:9 + 9 = 18 так подряпати 9 і написати 8; Крок 6:8 + 4 = 12 так подряпати 4 і написати 2; Крок 7:2 + 7 = 9 так напишіть 9 під бар, оскільки всі цифри були додані. Порахуйте подряпини (4), що позначає скільки десятків (40) і напишіть перед 9. Відповідь 49. Спробуйте проблему самостійно.

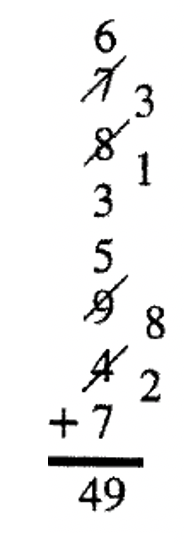
Вищезазначена проблема показує кожен крок, включаючи те, що ви думаєте, як ви йдете разом. Якби ви подивилися на проблему після того, як хтось це зробив, це виглядало б так, як ви бачите зліва. Більше прикладів наведено праворуч. Зберігати цифру пристрою в пам'яті швидше, ніж записувати їх на кожному кроці. Спробуйте обидва способи і десять прийняти те, що є найпростішим та/або швидшим для вас.
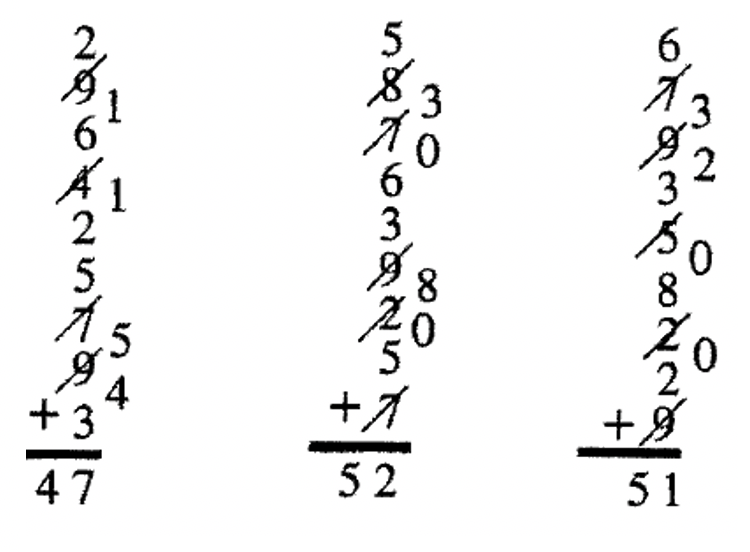
Використовуйте метод нуля, щоб додати наступні стовпці цифр. Складіть власну проблему з принаймні 12 чисел для частини е.
| а.\( \begin{aligned} 3 \\ 9 \\3 \\6\\5\\8\\6\\ \underline{+ 7} \end{aligned}\) | б.\( \begin{aligned} 5 \\ 3 \\ 9\\6\\7\\4\\2\\ \underline{+ 7} \end{aligned}\) | c.\( \begin{aligned} 8\\8\\5\\7\\9\\7\\6\\ \underline{+ 3} \end{aligned}\) | д.\( \begin{aligned} 7\\6\\4\\3\\8\\9\\7\\ \underline{+ 9} \end{aligned}\) | е. |
Методи Dot and Scratch можуть бути використані для додавання числівників з більш ніж однією цифрою. Додайте один стовпець за раз, залишаючи трохи місця між стовпцями для точок, якщо ви використовуєте метод Dot. Праворуч наведено приклад додавання за допомогою методу Scratch зі звичайним методом додавання справа наліво і перенесення. У цьому випадку я тримаю цифру кожного блоку в голові, на відміну від запису кожної цифри вниз після кожної подряпини. Перша колонка має чотири подряпини, тому 4 переноситься на колонку 2. ПРИМІТКА: Якщо ви не практикуєте кілька проблем, використовуючи ці методи, ймовірно, не буде простіше додати, використовуючи один із цих способів, ніж будь-який метод, який ви звикли використовувати. Але якщо ви практикуєте, ви, ймовірно, станете свистом на додаток і ніколи не повернетеся до старого шляху!
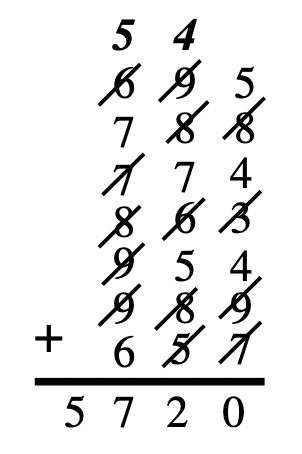
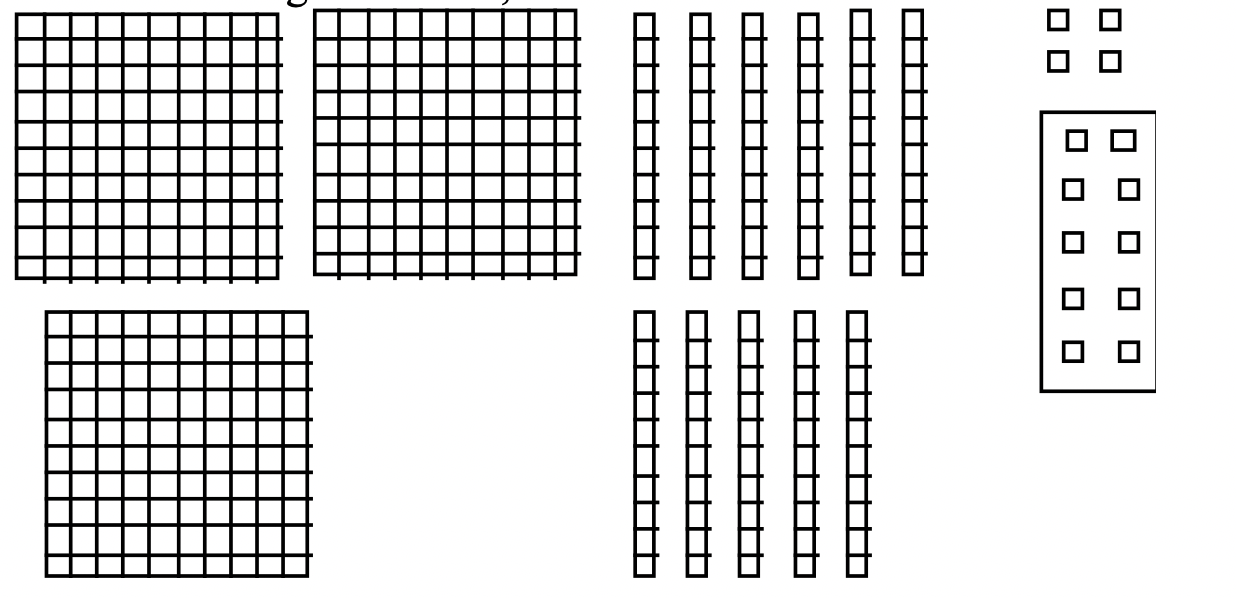
Найбільш поширеним алгоритмом додавання є стандартний алгоритм додавання справа наліво, який часто називають стандартним алгоритмом додавання. Це той, який майже кожен виріс, навчаючись. Ви починаєте справа і додаєте цифри. Під рядком проставляється цифра одиниці, а цифра десятка переноситься вгорі наступного стовпця зліва. Отримайте свої базові десять блоків зараз, щоб зрозуміти, що насправді відбувається.
Розглянемо проблему додавання 246 + 178. З наших знань про значення місця ми знаємо, що 246 це 2 100 + 4
10 + 6 (або 200 + 40 + 6) і 178 - 1
100 + 7
10 + 8 (або 100 + 70 + 8). Використовуючи блоки Base Ten, 246 будуть представлені з 2 квартирами, 4 лонгами та 6 одиницями, тоді як 178 будуть представлені 1 квартира, 7 лонг і 8 одиниць. Отже, проблему додавання можна придумати наступним чином:
Використання базових блоків
\ [\ почати {вирівняний} 2\ текст {плоский (и)} + 4\ текст {довгі (и)} +6\ текст {одиниці (и)}\
\ підкреслення {+ 1\ текст {плоский (и)} + 7\ текст {довгі (и)} + 8\ текст {одиниці (и)}}\ кінець {вирівняний}\ nonumber\]
Ця проблема додавання з використанням блоків показана нижче:
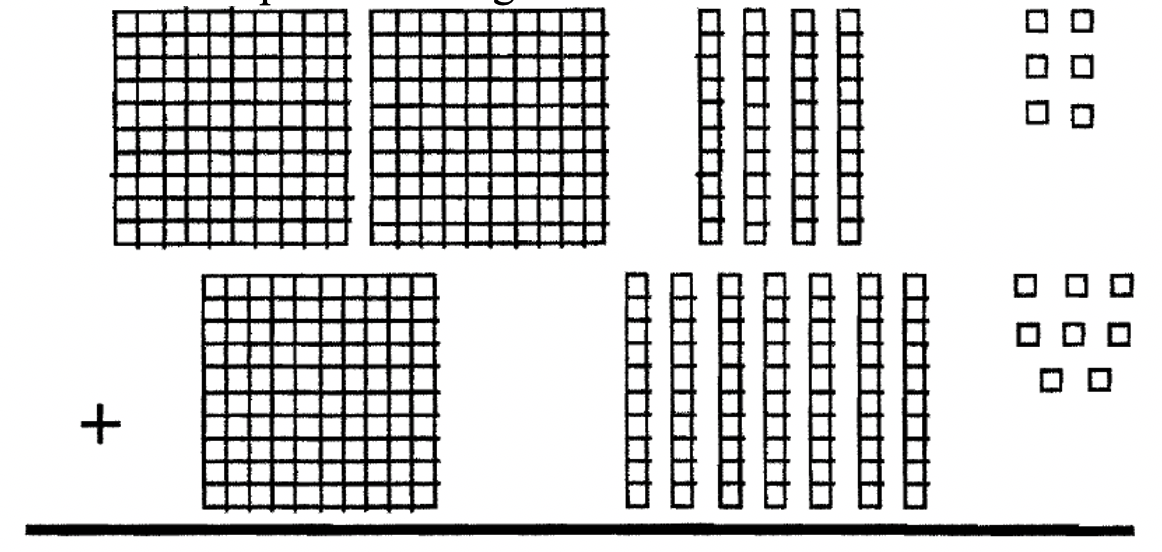
Якщо додати, то отримаємо:
\ [\ почати {вирівняний} 2\ текст {плоский (и)} + 4\ текст {довгі (и)} +6\ текст {одиниці (и)}\\ підкреслення {+ 1
\ текст {плоский (и)} + 7\ текст {довгі (и)} + 8\ текст {одиниці (и)}}\\ 3\ текст {плоскі (и)} +11\ текст {довгі (и)} +11\ текст {довгі (и)} +11\ текст {довгі (и)} +8\ текст {одиниці (и)} 14\ текст {одиниця (и)}\ кінець {вирівняний}\ nonumber\]
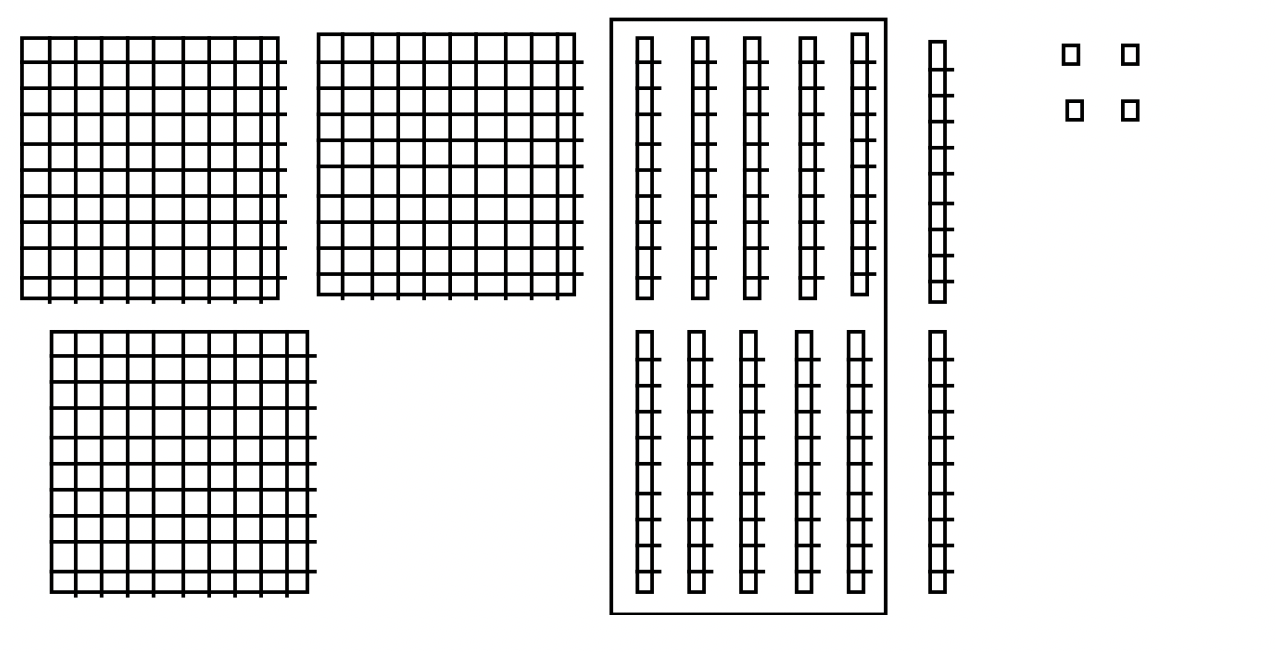
Торги тепер можна здійснювати. Десять з 14 одиниць можна обміняти на тривалий час. Це залишає нас з 3 квартирами, 12 лонг і 4 одиниці. Сума і угоди проілюстровані блоками на наступній сторінці.
Після торгів сума = 3 флет (и) + 12 лонг (ів) + 4 одиниці (ів)
Після об'єднання блоків сума показана нижче.
Наступний крок - торгувати десятьма одиницями протягом довгого часу. Я поставив коробку навколо одиниць, щоб торгувати вище. Це дає 3 квартири, 12 лонг і 4 одиниці, як показано нижче.
Тепер десять з 12 лонгів можна обміняти на квартиру. Я поставив коробку близько десяти з лонгів, щоб торгувати вище. Після обміну сума становить 4 квартири, 2 лонги і 4 одиниці, що становить 424. Це проілюстровано нижче.

Після того, як всі торгуються, остаточна сума = 4 флет (и) + 2 довгі (и) + 4 одиниці (и)
Ми знаходимося в базовій десятці, тому відповідь 424. Тому 246 + 178 = 424.
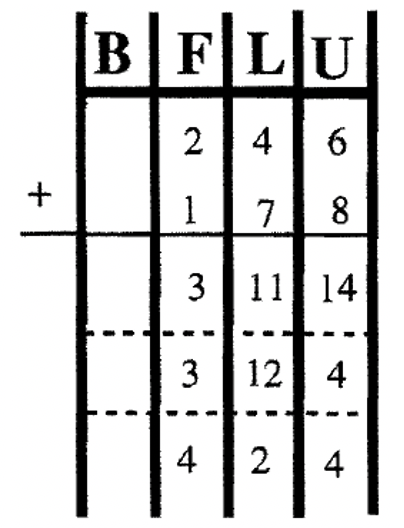
У попередньому прикладі додавання 246 + 178 за допомогою базових блоків десять лонгів можна було обміняти на квартиру одночасно, коли десять одиниць були обмінені на довгий час. Я робив лише одну торгівлю за раз, тому що в стандартному алгоритмі додавання ми не поєднуємо всі блоки (або розміщуйте значення) одночасно. Спочатку одиниці складаються разом, щоб отримати 14. 4 записується в колонку одиниці, а інші 10 одиниць записуються як 1 довгий в наступному стовпці, щоб означати, що є ще один довгий. Тепер є 1 + 4 + 7 лонгів, щоб скласти, що 12. 2 записано в стовпці лонгів, а інші 10 одиниць записуються як 1 квартира в наступному стовпці, щоб означати, що є ще одна квартира. Нарешті, є 1 + 2 + 1 квартири, щоб скласти, що 4. Таким чином, сума становить 4 квартири, 2 лонги і 4 одиниці, що становить 424. Обміни робляться - це те, що перенесення - це все про. Праворуч - ще один спосіб відстеження будинків, квартир, лонгів і одиниць. Зверніть увагу на торги, що здійснюються на кожному кроці. Якщо найбільший додаток має x цифр, я роблю x + 1 стовпці, щоб дозволити перенесення. У цій задачі є три цифри для кожного додатка, тому я зробив чотири стовпці, щоб дозволити можливий блок.
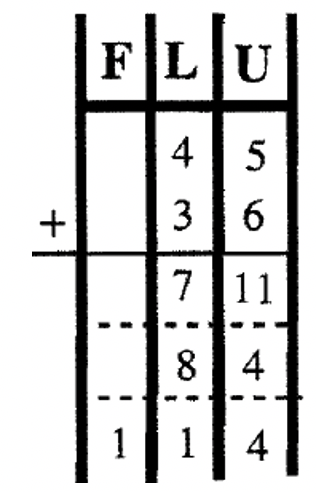
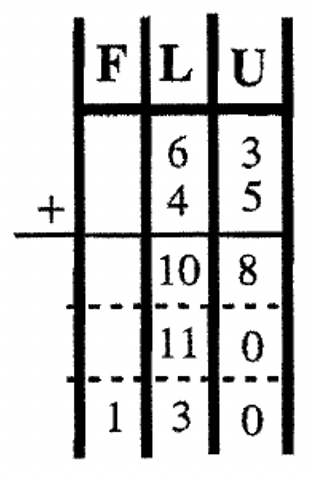
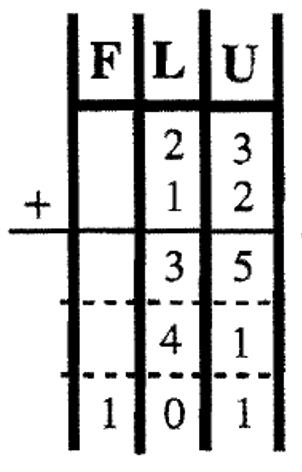
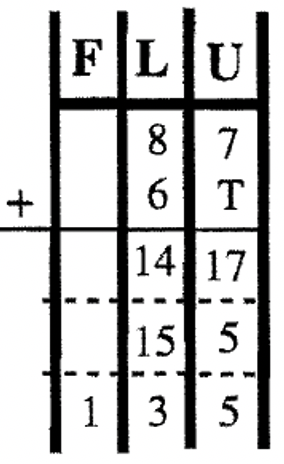
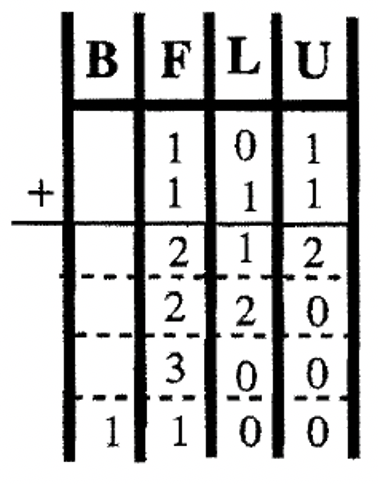
Тепер давайте виконаємо цей базовий алгоритм в інших базах. Якщо ви додаєте в Base Seven, хитрість тут полягає в тому, щоб згадати основні факти додавання в Base Seven. Ви повинні знати свої таблиці додавання. Пам'ятайте\(5_{\text{seven}} + 6_{\text{seven}} = 11_{\text{ten}}\), який є\(14_{\text{seven}}\) (який є одним довгим і чотирма одиницями в базовій сімки). Вивчіть приклади нижче. Щоб допомогти візуалізувати угоди, проблеми спочатку виконуються за допомогою діаграми з сумами, написаними в базовій десятці, щоб відстежувати одиниці, лонги, квартири тощо При обміні блоків, перетворення на належну одиницю здійснюється. Потім ті ж проблеми виконуються без використання діаграм та використання традиційного методу перенесення - тут ви додаєте базу, надану під час проходження. Спробуйте ці п'ять проблем самостійно, перш ніж переходити до наступної вправи.
| \(\begin{aligned} 45_{\text{seven}} \\ \underline{+36_{\text{seven}}} \end{aligned} \) | \(\begin{aligned} 63_{\text{eight}} \\ \underline{+ 45_{\text{eight}}} \end{aligned} \) | \(\begin{aligned} 23_{\text{four}} \\ \underline{+ 12_{\text{four}}} \end{aligned} \) | \(\begin{aligned}87_{\text{twelve}} \\ \underline{+ 6T_{\text{twelve}}} \end{aligned} \) | \(\begin{aligned} 101_{\text{two}} \\ \underline{+ 111_{\text{two}}} \end{aligned}\) |
 |
 |
 |
 |
 |
Ті ж приклади опрацьовані нижче за допомогою традиційного алгоритму перенесення.
| \(\begin{aligned} ^{1} \\& 45_{\text{seven}} \\& \underline{+36_{\text{seven}}} \\ & 114_{\text{seven}}\end{aligned} \) | \(\begin{aligned} ^{1} && ^{1} \\&63_{\text{eight}} \\ &\underline{+ 45_{\text{eight}}} \\& 130_{\text{eight}} \end{aligned} \) | \ (\ почати {вирівняний} &^ {1}\\ 23_ {\ текст {чотири}}\\ підкреслення {+ 12_ {\ текст {чотири}}}\\ 101_ {\ текст {чотири}}\ кінець {вирівняний}\) |
\ (\ почати {вирівняний} &^ {11}\ 87_ {\ текст {дванадцять}}\\\ підкреслення {+ 6T_ {\ текст {дванадцять}}\ 135_ {\ текст {дванадцять}}\\ текст {дванадцять}}\ кінець {вирівняний}\) |
\ (\ почати {вирівняний} 101_ {\ текст {два}}\\ підкреслення {+ 111_ {\ текст {два}}}\\ 1100_ {\ текст {два}}\ кінець {вирівняний}\) |
Додайте наступне. Виконайте кожну проблему, використовуючи діаграми, як показано в попередніх прикладах. Використовуйте свої базові блоки, щоб візуалізувати проблему далі.
| а.\(\begin{aligned} &7 & E && 1 & \ {}_{\text{thirteen}} \\ + & 5 &8 &&4& \ {}_{\text{thirteen}} \end{aligned}\) | б.\(\begin{aligned} &1 & 1 && 0 && 1 \ {}_{\text{two}} \\ +& 1 & 0 && 0 && 1 \ {}_{\text{two}} \end{aligned}\) | c.\(\begin{aligned} &3 & 2 && 0 && 4 \ {}_{\text{five}} \\ +& 4 & 0 && 1 && 3 \ {}_{\text{five}} \end{aligned}\) | д.\(\begin{aligned} &6 & 1 && 2 & \ {}_{\text{nine}} \\ + & 4 &5 &&6& \ {}_{\text{nine}} \end{aligned}\) |
 |
 |
 |
 |
| е.\(\begin{aligned} &1 &&0 & 1 && 1 && 1 \ {}_{\text{two}} \\ +&1&& 1 & 1 && 0 && 1 \ {}_{\text{two}} \end{aligned}\) | ф.\(\begin{aligned} 2&&2 && 1 && 2 & \ {}_{\text{three}} \\ + && 2 &&2 && 2 & \ {}_{\text{three}} \end{aligned}\) | г.\(\begin{aligned} &4 & 6 && 1 && 3 \ {}_{\text{twelve}} \\ +& 5 & T && 3 && 9 \ {}_{\text{twelve}} \end{aligned}\) | ч.\(\begin{aligned} &4 & 3 && 4 && 3 \ {}_{\text{seven}} \\ +& 4 & 1 && 4 && 5 \ {}_{\text{seven}} \end{aligned}\) |
 |
 |
 |
 |
Зрештою, ви повинні мати можливість робити вищезазначені проблеми без використання діаграм або маніпуляцій. Ви завжди можете думати з точки зору блоків, як ви їх працюєте. Додайте наступне, використовуючи традиційний алгоритм перенесення. Практикуйте, поки не відчуєте себе впевнено і не вмієте додавати без використання діаграм або маніпуляцій.
| а.\(\begin{aligned} &7 & E && 1 & \ {}_{\text{thirteen}} \\ + & 5 &8 &&4& \ {}_{\text{thirteen}} \end{aligned}\) | б.\(\begin{aligned} &1 & 1 && 0 && 1 \ {}_{\text{two}} \\ +& 1 & 0 && 0 && 1 \ {}_{\text{two}}\\ \hline \end{aligned}\) | c.\(\begin{aligned} &3 & 2 && 0 && 4 \ {}_{\text{five}} \\ +& 4 & 0 && 1 && 3 \ {}_{\text{five}}\\ \hline \end{aligned}\) | д.\(\begin{aligned} &6 & 1 && 2 & \ {}_{\text{nine}} \\ + & 4 &5 &&6& \ {}_{\text{nine}} \end{aligned}\) |
| е.\(\begin{aligned} &1 &&0 & 1 && 1 && 1 \ {}_{\text{two}} \\ +&1&& 1 & 1 && 0 && 1 \ {}_{\text{two}} \end{aligned}\) | ф.\(\begin{aligned} 2&&2 && 1 && 2 & \ {}_{\text{three}} \\ + && 2 &&2 && 2 & \ {}_{\text{three}}\\ \hline \end{aligned}\) | г.\(\begin{aligned} &4 & 6 && 1 && 3 \ {}_{\text{twelve}} \\ +& 5 & T && 3 && 9 \ {}_{\text{twelve}} \\ \hline \end{aligned}\) | ч.\(\begin{aligned} &4 & 3 && 4 && 3 \ {}_{\text{seven}} \\ +& 4 & 1 && 4 && 5 \ {}_{\text{seven}} \\ \hline \end{aligned}\) |
Інший спосіб додавання - це використання розширеного позначення. Наш перший приклад, 246 + 178, можна записати як (200 + 40 + 6) + (100 + 70 + 8). Використовуючи комутативні і асоціативні властивості, цю суму можна записати як (200 + 100) + (40 + 70) + (6 + 8) або 300 + 110 + 14 = 300 + (100 + 10) + (10 + 4) = (300 + 100) + (10 + 10) + 4 = 400 + 20 + 4 = 424. Коли виписано так, можливо, більш зрозуміло, що насправді додається, на відміну від того, щоб робити це методом, не замислюючись про місце вартості кожної цифри.
6. Додати за допомогою розширеної нотації. Показати всі кроки.
а. 43 + 47
б. 88 + 54
7. Припустимо, два різних учні складають два числа разом, як показано в двох задачах праворуч. Обидва мають дуже схожі методи. Поясніть, чим займається кожен студент і чому це має сенс. Потім, складіть ще дві проблеми і додайте, використовуючи один з цих методів.
| \(\begin{aligned}859 \\ \underline{+ 467} \\ 16 \\ 110 \\ \underline{+ 1200} \\ 1326 \end{aligned}\) | \(\begin{aligned}859 \\ \underline{+ 467} \\ 1200 \\ 110 \\ \underline{+ 16} \\ 1326 \end{aligned}\) |
Нижче наведено роботу трьох різних студентів, які роблять одну і ту ж проблему додавання. З'ясуйте, що робить кожен студент, щоб отримати відповідь, перш ніж читати далі.
| \(\begin{aligned}859 \\ \underline{+ 467} \\ 1200 \\ 1310 \\ 1326 \end{aligned}\) | \(\begin{aligned}859 \\ \underline{+ 467} \\ 1259 \\ 1319 \\ 1326 \end{aligned}\) | \(\begin{aligned}859 \\ \underline{+ 467} \\ 866 \\ 926 \\ 1326 \end{aligned}\) |
Перший студент починається з додавання сотень разом (800 + 400 = 1200). Далі десятки складаються разом (50 + 60 = 110) і ця відповідь додається на (1200 + 110 = 1310). Нарешті, додаються ті (9 + 7 = 16), і це додається, щоб отримати відповідь (1310 + 16 = 1326). Другий учень бере перше число і додає на сотні друге число (859 + 400 = 1259). Далі додаються десятки другого числа (1259 + 60 = 1319). Нарешті, ті додаються на (1319 + 7 = 1326). Третій учень починається з першого числа і додає на одиницях другої цифри першої (859 + 7 = 866). По-друге, додається десятка цифри другого числа (866 + 60 = 926). Нарешті, сотні додаються на (926 + 400 = 1326). Хтось може бути більш схильний використовувати один з цих методів, якщо вони додаються в голові.
Складіть власну проблему і вирішуйте, використовуючи три способи, описані вище. Поясніть метод та кроки, які використовуються для отримання правильної відповіді.
Інший метод, який використовується для додавання, - це алгоритм додавання зліва направо. Деякі з останніх кількох прикладів насправді використовують алгоритми зліва направо. У розширеній нотації ви можете додати зліва направо або справа наліво. Багато людей вважають алгоритм додавання зліва направо легше, оскільки немає перенесення. Існує пара способів виконання цього методу. Почніть з додавання крайнього лівого стовпчика цифр. Коли ви переходите до наступного стовпця праворуч, ви додаєте цифри. Якщо сума більше 9, напишіть цифру одиниці під цим стовпцем і підкреслюйте цифру, вже поставлену відразу ліворуч. Це схоже на перенесення, але вам не потрібно переходити до наступного стовпця - він додається до відповіді пізніше. Продовжуйте, поки не додасте цифри пристрою. Потім поверніться назад і додайте одну до всіх цифр, які підкреслені. Чи можете ви зрозуміти чому? Наступний приклад крок за кроком використовує цей алгоритм.
| Крок 1: Починаючи з крайнього лівого стовпця, додайте цифри (3 і 4). Оскільки 3 + 4 = 7, напишіть 7 під цим крайнім лівим стовпцем. | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline 7 & && && \end{aligned}\) |
| Крок 2: Додайте цифри в наступному стовпці праворуч. Починаючи з 6 + 8 = 14, напишіть 4 під цим стовпцем і підкреслюйте цифру зліва (\(\underline{7}\)). | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline \underline{7} && 4 && && \end{aligned}\) |
| Крок 3: Додайте цифри в наступному стовпці праворуч. Оскільки 3 + 2 дорівнює 5, напишіть 5 під цим стовпцем. | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline \underline{7} && 4 && 5 && \end{aligned}\) |
| Крок 4: Додайте цифри в наступному стовпці праворуч. Починаючи з 7 + 8 = 15, напишіть 5 під цим стовпцем і підкреслюйте цифру зліва (\(\underline{5}\)). | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline \underline{7} && 4 && \underline{5} && 5 \end{aligned}\) |
| Крок 5: Останній крок - переписати відповідь на проблему, додавши 1 до будь-якої цифри, яка підкреслена. Таким чином, відповідь - 8465. | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline \underline{7} && 4 && \underline{5} && 5 \\ 8 && 4 && 6 && 5 \end{aligned}\) |
Примітка. Крок 5 - це те, як виглядає проблема, коли вона виконана, як показано на прикладах нижче. Вивчіть, а потім спробуйте наступні приклади самостійно, перш ніж переходити до наступної вправи.
| \(\begin{aligned} 6483 \\ +5734 \\ \hline 1\underline{1} \underline{1} 1 7 \\ 12217 \end{aligned}\) | \(\begin{aligned} 5417 \\ +3971 \\ \hline \underline{8} 388 \\ 9388 \end{aligned}\) | \(\begin{aligned} 63925 \\ +41738 \\ \hline 10\underline{4}6 \underline{5} 3 \\ 105663 \end{aligned}\) | \(\begin{aligned} 787878 \\ +65656 \\ \hline \underline{7}\underline{4}\underline{2}\underline{4} \underline{2}4 \\ 853534 \end{aligned}\) |
| а.\(\begin{aligned} 5386 \\ \underline{+ 6723}\end{aligned}\) | б.\(\begin{aligned} 65381 \\\underline{+ 46082}\end{aligned}\) | c.\(\begin{aligned} 6789 \\ \underline{+ 9879}\end{aligned}\) | д.\(\begin{aligned} 70426 \\ \underline{+ 57908}\end{aligned}\) |
У алгоритмі зліва направо, коли 9 підкреслено, ви повинні продовжувати підкреслення, щоб включити цифру зліва від дев'яти (якщо ліворуч є цифра). Якщо цифра зліва дорівнює 9, продовжуйте підкреслення, щоб включити цифру зліва від неї. Продовжуйте підкреслювати, поки не підкреслите цифру, яка не є дев'яткою. Потім, коли ви повернетеся назад, додайте до підкресленого числа 1, (яке тепер буде більше однієї цифри). Вивчіть, а потім практикуйте наступні чотири приклади самостійно, перш ніж спробувати наступну вправу.
| \(\begin{aligned} 4672 \\ \underline{+ 5826} \\ \underline{9} 498 \\ \\ 10498 \end{aligned}\) | \(\begin{aligned} 8468 \\ \underline{+ 5538} \\ 1 \underline{399} 6 \\ \\ 14006 \end{aligned}\) | \(\begin{aligned} 5798 \\ \underline{+ 4605} \\ \underline{9} \underline{39}3 \\ \\ 10403 \end{aligned}\) | \(\begin{aligned} 35776 \\ \underline{+ 64525} \\ \underline{99} \underline{29}1 \\ \\ 100301 \end{aligned}\) |
Використовуючи цю техніку, перший приклад додає від 1 до 9, щоб отримати 10. У другому прикладі 1 додається до 399, щоб отримати 400. У третьому прикладі 1 додається до 9, щоб отримати 10, а 1 додається до 39, щоб отримати 40. У четвертому прикладі 1 додається до 99, щоб отримати 100, а 1 додається до 29, щоб отримати 30.
Використовуйте алгоритм зліва направо, щоб додати наступні числа, використовуючи вищевказану техніку.
| а.\(\begin{aligned} 7658 \\ \underline{+ 1147}\end{aligned}\) | б.\(\begin{aligned} 4804 \\\underline{+ 5659}\end{aligned}\) | c.\(\begin{aligned} 5679 \\ \underline{+ 7350}\end{aligned}\) | д.\(\begin{aligned} 98765 \\ \underline{+ 7238}\end{aligned}\) |
На наступній сторінці наведено деякі проблеми додавання в інших базах. Алгоритм додавання зліва направо використовується. Будьте уважні, зверніть увагу на підставу. Наприклад, у Base Six кожного разу, коли ви додаєте та отримуєте число вище 5 (що є найвищою цифрою в базовій шістці), ви записуєте лише цифру одиниці під цим стовпцем і підкреслюєте цифру зліва. У Base Three кожного разу, коли ви додаєте та отримуєте число вище 2 (що є найвищою цифрою в базовій третій), ви записуєте лише цифру одиниці під цим стовпцем і підкреслюєте цифру зліва від неї. У Base Twelve кожного разу, коли ви додаєте та отримуєте число вище E (що є найвищою цифрою в Base Twelve), ви записуєте лише цифру одиниці під цим стовпцем і підкреслюєте цифру зліва від неї. Переконайтеся, що ви розумієте і можете зробити ці наступні приклади успішно самостійно, перш ніж перейти до наступного абзацу та прикладів.
| \(\begin{aligned} 423 \ {}_{\text{six}} \\ \underline{+503} \ {}_{\text{six}} \\ 13\underline{2}0 \ {}_{\text{six}} \\ 1330 \ {}_{\text{six}} \end{aligned}\) | \(\begin{aligned} 839 {}_{\text{twelve}} \\ \underline{+ E58} \ {}_{\text{twelve}} \\ 17\underline{8}5 \ {}_{\text{twelve}} \\ 1795 \ {}_{\text{twelve}}\end{aligned}\) | \(\begin{aligned}580 \ {}_{\text{nine}} \\ \underline{+ 723} \ {}_{\text{nine}} \\ 1\underline{3}13 \ {}_{\text{nine}} \\ 1413 \ {}_{\text{nine}}\end{aligned}\) | \(\begin{aligned}1011 \ {}_{\text{two}} \\ \underline{+ 1011} \ {}_{\text{two}} \\ 10\underline{0}\underline{0}0 \ {}_{\text{two}} \\ 10110 \ {}_{\text{two}}\end{aligned}\) | \(\begin{aligned}2012 \ {}_{\text{three}} \\ \underline{+ 1112} \ {}_{\text{three}} \\ 10\underline{1}\underline{2}1 \ {}_{\text{three}} \\ 10201 \ {}_{\text{three}}\end{aligned}\) |
Нижче наведено кілька прикладів, де вам потрібно зробити деяке безперервне підкреслення, подібне до прикладів, показаних раніше в Base Ten. Приділіть пильну увагу підстави. Якщо ви підкреслюєте 5 в Base Six, ви повинні продовжувати підкреслювати цифру зліва, поки не підкреслите цифру менше 5! Якщо ви підкреслюєте 2 в Base Three, ви повинні продовжувати підкреслювати цифру зліва, поки не підкреслите цифру менше 2! Якщо ви підкреслюєте E в Base Twelve, ви повинні продовжувати підкреслювати цифру ліворуч, доки ви не підкреслите цифру менше E!. Вивчіть і практикуйте п'ять прикладів нижче самостійно, перш ніж спробувати наступну вправу.
| \(\begin{aligned} 324 \ {}_{\text{six}} \\ \underline{+132} \ {}_{\text{six}} \\ \underline{45}0 \ {}_{\text{six}} \\ 500 \ {}_{\text{six}} \end{aligned}\) | \(\begin{aligned} 367 \ {}_{\text{twelve}} \\ \underline{+ 35E} \ {}_{\text{twelve}} \\ \underline{6E}6 \ {}_{\text{twelve}} \\ 706 \ {}_{\text{twelve}}\end{aligned}\) | \(\begin{aligned} 528 \ {}_{\text{nine}} \\ \underline{+367} \ {}_{\text{nine}} \\ \underline{88}6 \ {}_{\text{nine}} \\ 1006 \ {}_{\text{nine}}\end{aligned}\) | \(\begin{aligned} 1011 \ {}_{\text{two}} \\ \underline{+1110} \ {}_{\text{two}} \\ 1\underline{01}01 \ {}_{\text{two}} \\ 11001 \ {}_{\text{two}}\end{aligned}\) | \(\begin{aligned} 22021 \ {}_{\text{three}} \\ \underline{+1002} \ {}_{\text{three}} \\ \underline{2}0\underline{02}0 \ {}_{\text{three}} \\ 100100 \ {}_{\text{three}}\end{aligned}\) |
Вправа 11
Використовуйте алгоритм додавання зліва направо, щоб додати наступне. Зверніть пильну увагу на базу!!!
| а.\(\begin{aligned} 514 \ {}_{\text{six}} \\ \underline{ + 342 \ {}_{\text{six}}} \end{aligned}\) | б.\(\begin{aligned}835 \ {}_{\text{eleven}} \\ \underline{ + 658 \ {}_{\text{eleven}}} \end{aligned}\) | c.\(\begin{aligned}473 \ {}_{\text{eight}} \\ \underline{ + 473 \ {}_{\text{eight}}} \end{aligned}\) | д.\(\begin{aligned}1111 \ {}_{\text{two}} \\ \underline{ + 1010 \ {}_{\text{two}}} \end{aligned}\) | а.\(\begin{aligned}2034 \ {}_{\text{five}} \\ \underline{ + 1112 \ {}_{\text{five}}} \end{aligned}\) |
| ф.\(\begin{aligned}7E1 \ {}_{\text{thirteen}} \\ \underline{ + 584 \ {}_{\text{thirteen}}} \end{aligned}\) | ф.\(\begin{aligned}1101 \ {}_{\text{two}} \\ \underline{ + 1001 \ {}_{\text{two}}} \end{aligned}\) | ф.\(\begin{aligned}3204 \ {}_{\text{five}} \\ \underline{ + 4013 \ {}_{\text{five}}} \end{aligned}\) | ф.\(\begin{aligned}612 \ {}_{\text{nine}} \\ \underline{ + 456 \ {}_{\text{nine}}} \end{aligned}\) |
| j.\(\begin{aligned}10111 \ {}_{\text{two}} \\ \underline{ + 11101 \ {}_{\text{two}}} \end{aligned}\) | к.\(\begin{aligned}2212 \ {}_{\text{three}} \\ \underline{ + 222_{\text{three}}} \end{aligned}\) | л.\(\begin{aligned}4613_{\text{twelve}} \\ \underline{ + 5T39_{\text{twelve}}} \end{aligned}\) | м.\(\begin{aligned}4343_{\text{seven}} \\ \underline{ + 4145_{\text{seven}}} \end{aligned}\) |
Перерахуйте всі бази від двох до тринадцяти, в яких кожна з наступних проблем додавання є дійсною.
| а.\(\begin{aligned} 403 \\ \underline{+ 542} \\ 1245 \end{aligned}\) | б.\(\begin{aligned}729\\ \underline{+ 526} \\ W52\end{aligned}\) | c.\(\begin{aligned}E83\\ \underline{+ 1T3} \\ 1166\end{aligned}\) | д.\(\begin{aligned}1011\\ \underline{+ 1111} \\ 2122\end{aligned}\) | е.\(\begin{aligned}2012\\ \underline{+ 1011} \\ 3023\end{aligned}\) |
Хтось почав робити кожну з цих проблем додавання, використовуючи стандартний алгоритм справа наліво. З'ясуйте, в якій основі знаходиться кожна проблема додавання, і закінчити обчислення.
| а.\(\begin{aligned} 64 \\ \underline{+ 46} \\ 2 \end{aligned}\) | б.\(\begin{aligned}53\\ \underline{+ 28} \\ 2\end{aligned}\) | c.\(\begin{aligned}21\\ \underline{+ 12} \\ 0\end{aligned}\) | д.\(\begin{aligned}57\\ \underline{+ 66} \\ 3\end{aligned}\) |
Хтось додавав 47 + 68 в голові і сказав вголос: «47 + 70 = 117 і два менше 115». Поясніть її міркування.
Інша людина додала 47 + 68 в голові і сказала вголос «40 + 60 - 100, а 8 + 7 - 15, тому відповідь 115». Поясніть його міркування.
Методи у вправах 14 і 15 можна назвати методами Break-Apart. Ви розбиваєте один або обидва додатки, використовуючи місце значення числа. Подумки обчислити 97 + 88, а потім пояснити метод, який ви використовували.
Чи є якісь додаткові хитрощі, які ви використовуєте? Додатковий кредит для обміну на Форумі
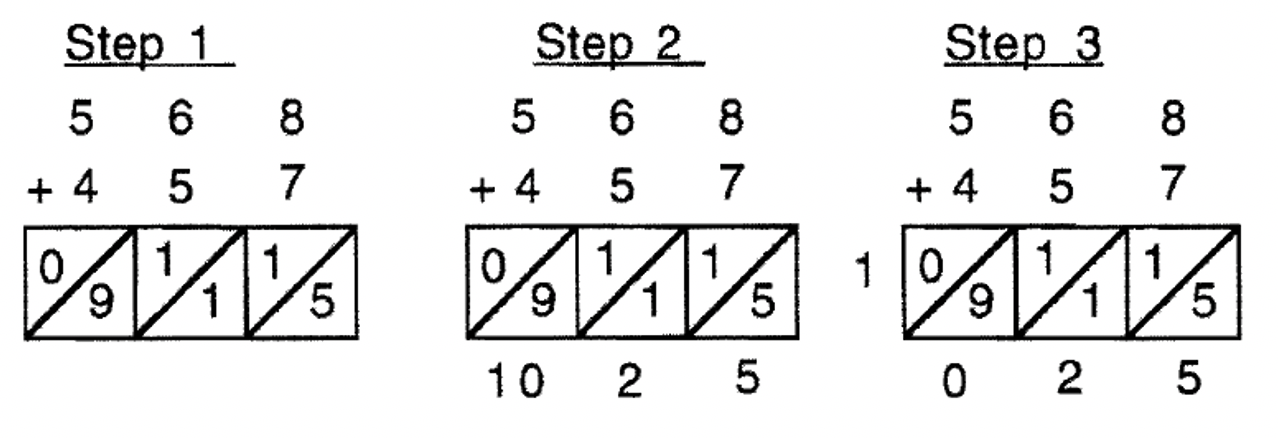
Нижче наведено ще один алгоритм додавання, який називається Метод решітки для додавання, який використовується для складання двох чисел разом. Спочатку складаємо стовпчики вниз, потім вниз по діагоналі. Проблема додавання - 568 + 457, а відповідь - 1,025. Подивіться, чи зможете ви зрозуміти, як це зробити, і зрозуміти, чому це працює. Ми будемо використовувати метод решітки знову, коли ми робимо множення.
Використовуйте метод решітки для обчислення 456 + 659. Покажіть свою роботу.
Використовуйте метод решітки, щоб обчислити наступне:
| а.\(12_{\text{six}} + 25_{\text{six}}\) | б.\(T4E_{\text{thirteen}} + 190_{\text{thirteen}}\) |
Навчитися оцінювати - дуже корисний навик. Ідея полягає в тому, щоб перетворити фактичні числа в задачі на більш прості числа, які легко обчислити подумки. У вправі 14, 47 + 68 близький до додавання 50 + 70, що 120. 120 досить близько - це в межах 5% від точної відповіді 115. Навіть якщо вам потрібно знати точну відповідь, якщо ви робите швидку оцінку, ви зазвичай можете сказати, чи перебуваєте ви в парку для м'ячів. Іноді оцінка - це все, що дійсно необхідно. Наприклад, якщо ви робите покупки для продуктів і маєте обмежену кількість готівки на руках, щоб заплатити за них, ви можете подумки скласти те, що ви витрачаєте, коли йдете разом. Найшвидший спосіб оцінити - це округлити. І якщо ви хочете переконатися, що ви не перевищуєте виділену суму, ви завжди можете просто округлити. Припустимо, у вас в кошику було десять товарів на такі суми:
| $6,75 | $3.23 | $1.25 | $7.18 | $2.98 | $1.89 | $1.50 | $2.45 | $3,69 | $1.76 |
Є багато способів округлити та додати - ви можете округлити до найближчого долара або до найближчого долара (щоб переконатися, що ви не перейдете) або, можливо, до найближчих 50 центів. Я збираюся припустити, що ви вже знаєте, як округлити числа. І ви повинні бути в змозі додати в голові, використовуючи пальці і Dot Method. Нижче наведено три приклади того, як ви можете отримати оцінку того, що буде продуктовий рахунок.
| Округлення до найближчого долара: 7 + 3 + 1 + 7 + 3 + 2 + 2 + 2 + 4 + 1 = 32 |
| Округлення до найближчого долара: 7 + 4 + 2 + 8 + 3 + 2 + 2 + 3 + 4 + 1 = 36 |
| Округлення до найближчих 50 копійок: 7 + 3 + 1,5 + 7 + 3 + 2 + 1,5 + 2,5 + 3,5 + 1 = 32 |
Фактична сума становить $31.68, що надзвичайно близько до нашої приблизної оцінки $32, яку ми отримали округлення як до найближчого долара, так і до найближчих 50 центів. Якщо ви працюєте з більш високими цінами предметів, ви можете округлити до найближчих десяти або ста доларів тощо.
Подумки оцініть вартість продуктового рахунку, що містить наступні цінові предмети. Поясніть, як ви це зробили. Потім порівняйте свою відповідь з фактичною сумою.
| $4.67 | $8.21 | $9.53 | $5.33 | $2.79 | $1.89 | $2.14 | $4.65 | $5.14 | $0.83 |
Уявіть, що ви йдете по магазинах, і ви купуєте десять предметів, де кожен елемент менше $10. Перерахуйте фактичну вартість кожної позиції (складіть їх) і оцініть загальну суму. Потім обчислити фактичну вартість десяти пунктів.
Коли ви думаєте, що ви можете отримати занадто високу або низьку оцінку? Наведемо приклад.
