3.2: Поєднання
- Page ID
- 66891
Вам знадобиться: Базові блоки (Матеріальні карти 4-15)
Ми почнемо цей набір вправ з з'ясування того, як скласти в єгипетській системі числення. Вам нагадують символи та їх індуї-арабські еквіваленти нижче:
| | (1) |
 (10) |
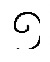 (100) |
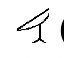 (1 000) |
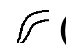 (10 000) |
 (100 000) |
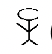 (1 000 000) |
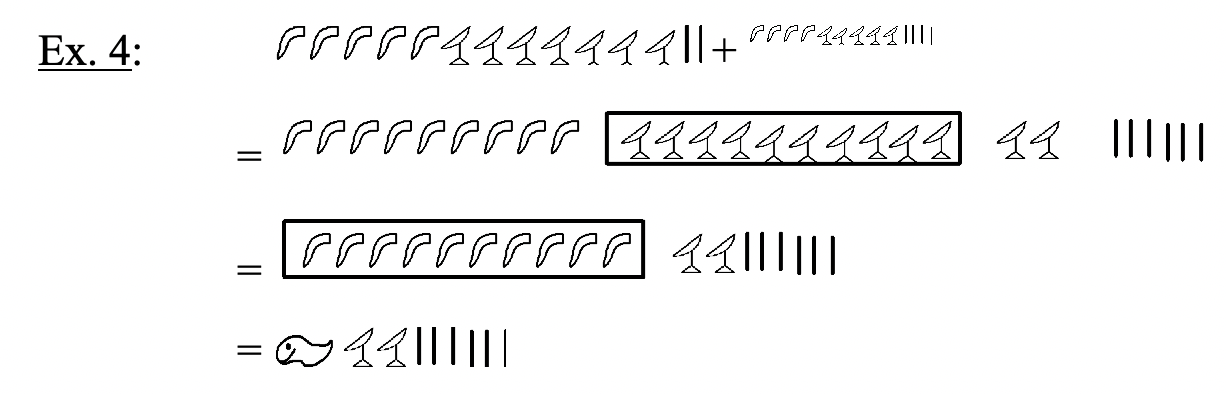
Оскільки єгипетська система числення є базовою адитивною системою, сума двох чисел утворюється простим об'єднанням символів з обох числівників разом. Оскільки це система Base Ten, обмін може бути здійснений у будь-який час, коли є десять одного символу, замінивши десять одного символу для наступного вищого символу. Щоб показати, що відбувається обмін, ви можете обвести, поставити коробку навколо або підкреслити десять того ж символу. У наступних прикладах біржі позначаються, поставивши поле навколо групи з десяти символів, які повинні бути замінені новим символом на наступному кроці. Після кожного обміну може знадобитися зробити ще один обмін. Вивчіть наступні приклади єгипетських проблем додавання. Спробуйте думати в єгипетському, як ви робите це, просто дотримуючись правил об'єднання та обміну, на відміну від мислення про те, що цифри кожна цифра розшифровується в індуї-арабською мовою. Пропрацювавши кожну проблему, ви завжди можете повернутися назад і перевірити, спочатку перетворивши кожну з додаються числівників (доповнення) на індуї-арабську, склавши їх разом, а потім перевіривши, чи сума узгоджується з відповіддю, отриманою в єгипетській мові.
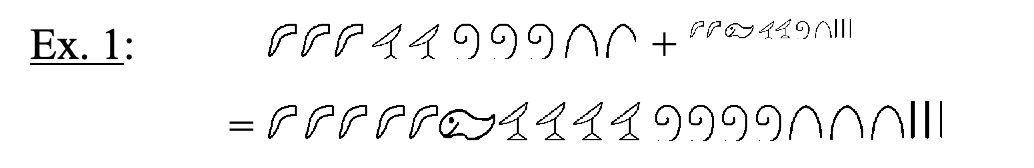 |
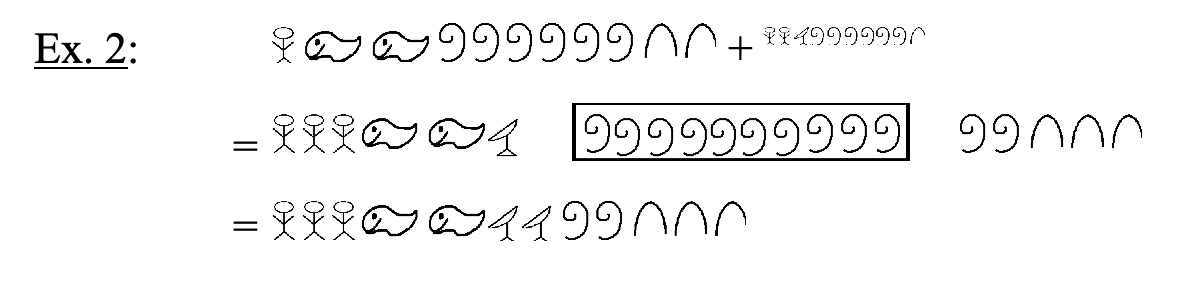 |
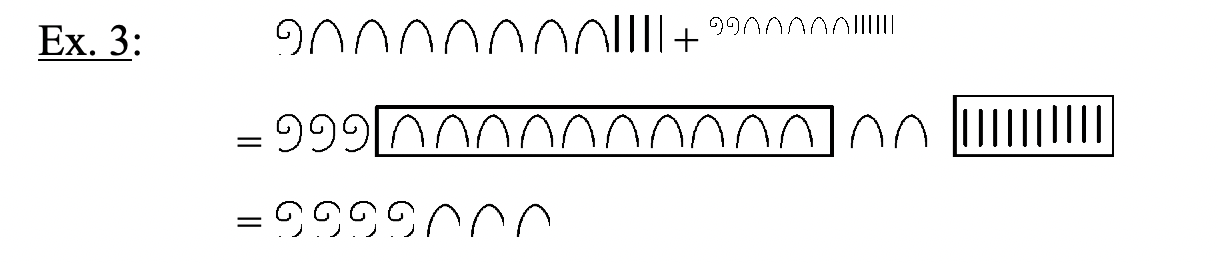 |
 |
Додайте наступні єгипетські числівники. Показати всі кроки, вказавши будь-які зроблені обміни. Знову ж таки, спробуйте працювати через них, думаючи лише єгипетською мовою. Ви завжди можете повернутися назад і перевірити, коли ви закінчите, роблячи їх на індуї-арабською мовою. Складіть власні проблеми для частини е і частини f.
|
а. 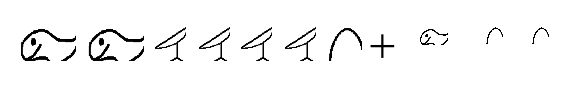 |
|
б. 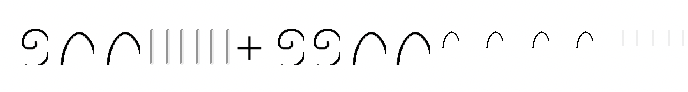 |
|
c. 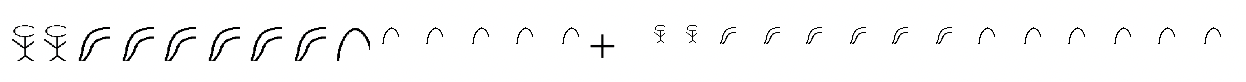 |
|
д. 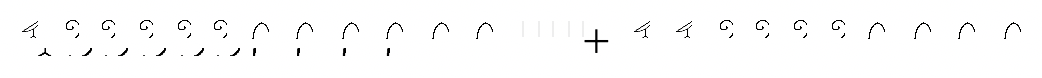 |
Давайте зробимо вигляд, що наша нинішня система грошей була строго в базовій десятці, так що єдиною валютою, яку ми використовували, були копійки, копійки, купюри в один долар, десятидоларові купюри, сто доларові купюри, тисячі доларових купюр і так далі. Замість малювання зображень грошей будуть використані ці скорочення для кожного виду монети або купюри: пенні (A), копійки (B), купюра в один долар (C), десятидоларова купюра (D), стодоларова купюра (E), тисячна купюра (F) і так далі. Оскільки більшість з вас розглядає можливість вступу до викладацької професії, вам, мабуть, не потрібно буде обробляти що-небудь вище, ніж тисяча доларів. Принаймні так, як я пишу це в 1999 році, але хто знає, що має майбутнє, правда?
Покажіть, які обміни можна здійснити для кожного з наступних дій:
| а. ааааааааааа = ____ | б. CCCCCCCCCC = ____ | с. FFFFFFFFFF = ____ |
Сформуйте кожну суму, об'єднавши два додатки в одну одноразову. Зробіть обмін в міру необхідності, щоб сума була представлена найменшою кількістю монет або купюр. Показати всі кроки, вказавши будь-які зроблені обміни.
| а. CCAADDCB + BBBBBBBBAACC |
| б. АААААЦККККККСЦЦЕЕЕЕ+ККККББВ |
| c ЕЕЕЕЕЕЕЕЕАААААААА+ЕЕЕААА |
| d. ДДДДКККБББББББ+ДДДДДККБББББББББ |
Щоб додати в системі майя, першим кроком є об'єднання символів на кожному рівні разом. Символи на кожному рівні повинні поєднуватися окремо. Потім на кожному рівні подивіться, чи можна зробити якісь обміни. Групу з п'яти точок завжди можна обміняти на відрізок лінії. Обмін з одного рівня на наступний трохи складніше. Група з 20 на одному рівні може торгуватися на одну точку на наступному рівні вгору, за винятком від другого до третього рівня, де група з 18 на другому рівні може торгуватися за одну точку на третьому рівні. Вивчіть наступні приклади одного рівня числівників майя, що складаються разом. Кожен раз, коли відбувається обмін, коло або коробка буде поставлена навколо того, що буде замінено на наступному кроці. Стрілка буде використовуватися, щоб вказати, чи відбувається обмін з одного рівня на наступний рівень вгору. Стрілка вказує, що точка буде на наступному рівні вгору на наступному кроці замість суми в коробці на початковому рівні. Дивіться приклад 2 нижче: Від кроку 2 до кроку 3 чотири відрізки лінії на першому рівні замінюються крапкою на другому рівні.
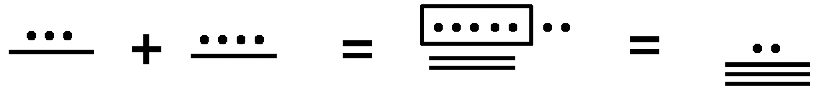
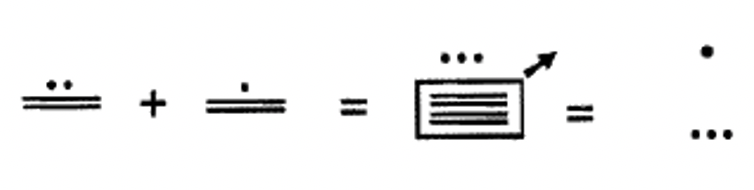

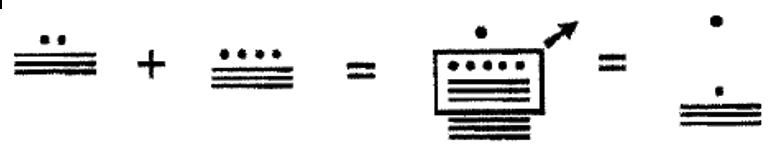
Додайте наступні однорівневі цифри майя разом. Зробіть будь-які необхідні обміни і покажіть всі кроки.
|
а. 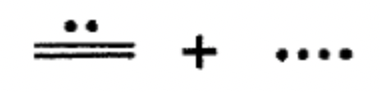 |
|
б. 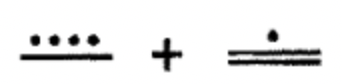 |
|
c. 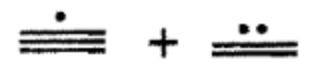 |
Вивчіть наступні приклади на цій та наступній сторінці додавання числівників майя разом. Все це більше одного рівня. Великі простори використовуються для розмежування між різними рівнями. Спробуйте зробити їх самостійно на власному папері.
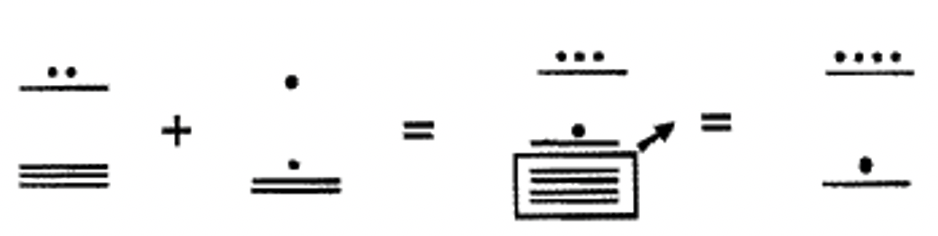


Пам'ятайте, групу з 18 на другому рівні можна обміняти на точку на третьому рівні!
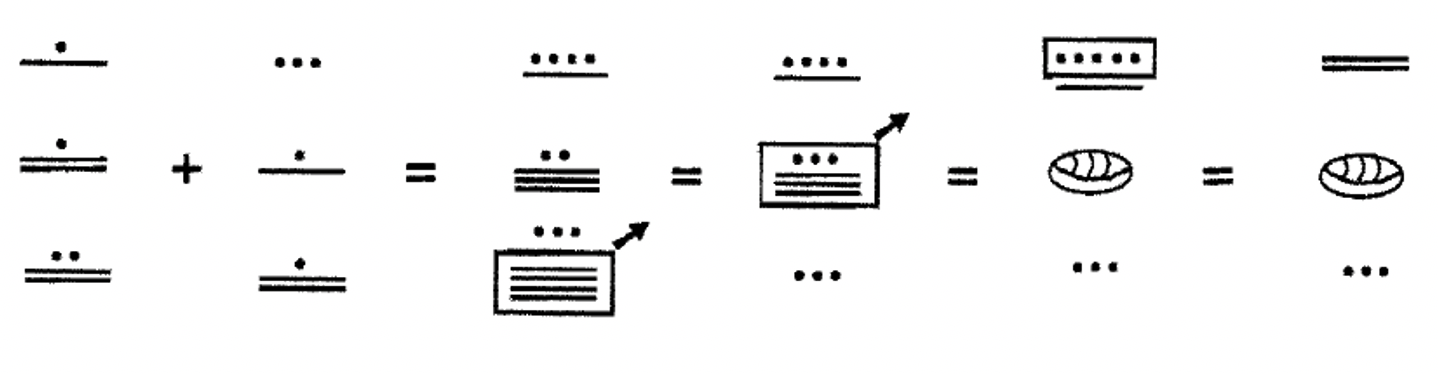
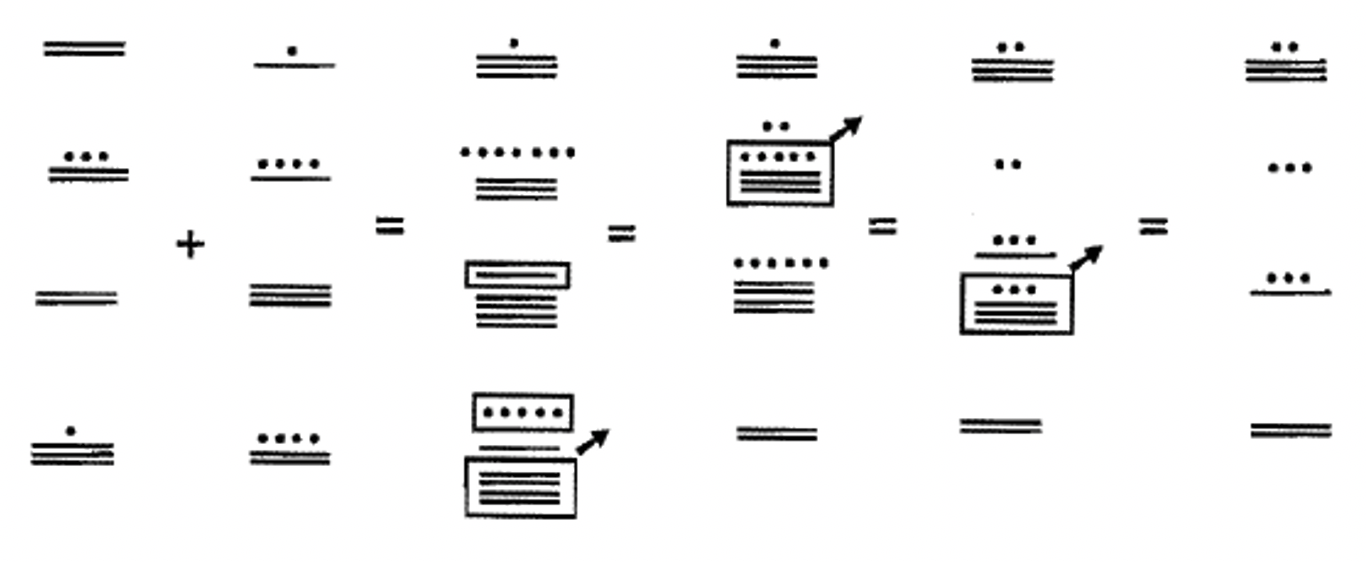
Після виконання кожного з наведених вище прикладів виключно в майя, я перевірив кожну проблему, перетворивши кожен додаток на індуїстсько-арабську, додавши в базовій десятці, перетворюючи суму в майя і переконавшись, що відповідь узгоджена з відповіддю, яку я отримав. Коли я перевірив приклад 5 (76,896 + 46,754 = 123,650), досить складна проблема, вона не перевіряла. Так що я переробив проблему, поки я не отримав це право. Це гарна ідея, щоб перевірити вашу роботу ретельно, як ви йдете вперед, що вимагає сильних доз концентрації, зусиль і терпіння. В іншому випадку досить легко зробити одну або кілька помилок під час обчислень. Майте на увазі, що якщо все, що ви робите, це перетворити на індуї-арабську, додати і перетворити назад на майя, ви не отримаєте кредит, тому що це не покаже всі кроки, пов'язані, об'єднання, обмін тощо, які ви зобов'язані показати, коли ви виконуєте вправи. Спробуйте кожен з наведених вище прикладів на окремому аркуші паперу, щоб переконатися, що ви працюєте з ними правильно. Зауважте, що послідовність кроків, показана для кожного з прикладів, може бути не єдиним способом отримати правильну відповідь.
Складіть наступні числівники майя разом. Зробіть будь-які необхідні обміни і покажіть всі кроки. Це дуже гарна ідея, щоб перевірити свою роботу, і це не означає, що шукати відповідь у рішеннях! Після додавання в майя, перетворіть відповідь на індуї-арабську. Потім перетворіть оригінальні два числа на індуї-арабську мову і складіть разом і подивіться, чи відповідає вона відповіді.
|
а. 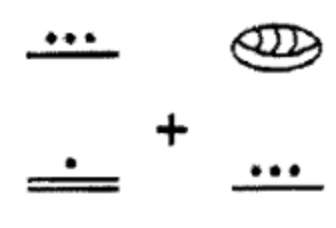 |
|
б. 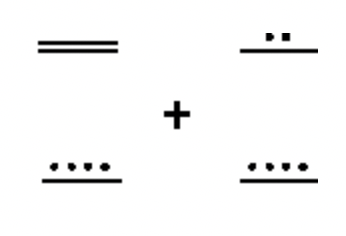 |
|
c. 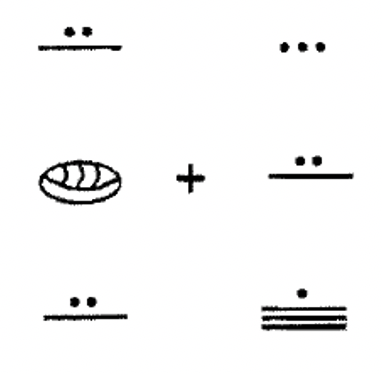 |
|
д. 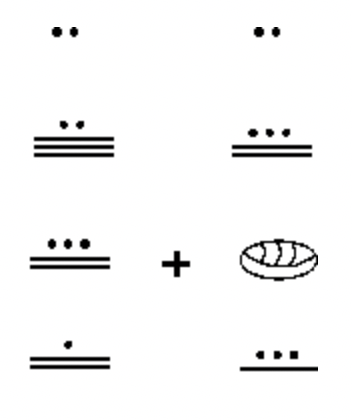 |
|
е.  |
Підрахуйте 15 одиничних блоків і зробіть обмін з базовими чотирма блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін в базовій четвірці, напишіть 15 як основу чотири цифри на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 13 одиниць і зробіть обмін з базовими чотирма блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обміни в базовій четвертій основі, напишіть 13 як базову чотири цифри на просторі, передбаченому для купи B нижче. Щоб додати, просто об'єднайте блоки з Pile A і Pile B, щоб сформувати одну велику купу блоків. Ви формуєте об'єднання палі A і ворсу B! Зробіть всі можливі обміни базовими чотирма блоками, а потім запишіть кількість одиниць у об'єднаній купі як основу чотири цифри на наданому просторі.
Поєднання двох паль таке ж, як і формування суми двох числівників. Ви тільки що додали два числа разом в іншій базі.
Нижче наведено проблему додавання, яку ви щойно виконали в Base Four.
____________ + _____________ = ____________
Ворс A Ворс B Комбінований ворс
Підрахуйте 15 одиничних блоків і зробіть обмін базовими сімома блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін в базовій семи, напишіть 15 як базовий сім числівник на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 13 одиниць і зробіть обмін базовими сімома блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обміни в базовій семи, напишіть 13 як базову сім числівників на просторі, передбаченому для купи B нижче. Щоб додати, просто об'єднайте блоки з Pile A і Pile B, щоб сформувати одну велику купу блоків. Ви формуєте об'єднання палі A і ворсу B! Зробіть всі можливі обміни базовими сімома блоками, а потім напишіть кількість одиниць у комбінованій купі як основу сім числівників на просторі, наданому нижче.
Поєднання двох паль таке ж, як і формування суми двох числівників. Ви тільки що додали два числа разом в іншій базі.
Нижче наведено проблему додавання, яку ви щойно виконали в Base Seven
____________ + _____________ = ____________
Ворс A Ворс B Комбінований ворс
Підрахуйте 15 одиничних блоків і зробіть обмін з базовими двома блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін у базі два, напишіть 15 як основу дві цифри на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 13 одиниць і зробіть обмін з базовими двома блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обмін у базі два, напишіть 13 як основу дві цифри на просторі, передбаченому для купи B нижче. Щоб додати, просто об'єднайте блоки з Pile A і Pile B, щоб сформувати одну велику купу блоків. Ви формуєте об'єднання палі A і ворсу B! Зробіть всі можливі обміни з базовими двома блоками, а потім запишіть кількість одиниць у об'єднаній купі як основу двох числівників на наданому просторі.
Поєднання двох паль таке ж, як і формування суми двох числівників. Ви тільки що додали два числа разом в іншій базі.
Нижче наведено проблему додавання, яку ви щойно виконали в Base Two.
____________ + _____________ = ____________
Ворс A Ворс B Комбінований ворс
Підрахуйте 15 одиничних блоків і зробіть обмін з базовими дев'ятьма блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін на основі дев'яти, напишіть 15 як базову дев'ять числівників на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 13 одиниць і зробіть обміни з базовими дев'ятьма блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обмін у дев'ятій основі, напишіть 13 як базову дев'ять числівників на просторі, передбаченому для купи B нижче. Щоб додати, просто об'єднайте блоки з Pile A і Pile B, щоб сформувати одну велику купу блоків. Ви формуєте об'єднання палі A і ворсу B! Зробіть всі можливі обміни з базовими дев'ятьма блоками, а потім запишіть кількість одиниць у комбінованій купі як основу дев'ять числівників на наданому просторі.
Поєднання двох паль таке ж, як і формування суми двох числівників. Ви тільки що додали два числа разом в іншій базі.
Нижче наведено проблему додавання, яку ви щойно виконали в Base Nine.
____________ + _____________ = ____________
Ворс A Ворс B Комбінований ворс
Підрахуйте 15 одиничних блоків і зробіть обмін з базовими трьома блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін в базі три, напишіть 15 як основу три цифри на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 13 одиниць і зробіть обмін з базовими трьома блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обмін в основі три, напишіть 13 як основу три цифри на просторі, передбаченому для купи B нижче. Щоб додати, просто об'єднайте блоки з Pile A і Pile B, щоб сформувати одну велику купу блоків. Ви формуєте об'єднання палі A і ворсу B! Зробіть всі можливі обміни з базовими трьома блоками, а потім напишіть кількість одиниць у об'єднаній купі як основу три цифри на просторі, наданому нижче.
Поєднання двох паль таке ж, як і формування суми двох числівників. Ви тільки що додали два числа разом в іншій базі.
Нижче наведено проблему додавання, яку ви щойно виконали в Base Three
____________ + _____________ = ____________
Ворс A Ворс B Комбінований ворс
Підрахуйте 15 одиничних блоків і зробіть обмін з базовими вісьмома блоками. Покладіть їх у стопку, яка називається Pile A, і ЗБЕРЕЖІТЬ ЦЮ СТОПКУ. Оскільки ви зробили обмін у базовій вісім, напишіть 15 як базову вісім цифр на просторі, передбаченому для купи A нижче. Тепер порахуйте ще 13 одиниць і зробіть обміни з базовими вісьмома блоками. Покладіть їх у купу, яка називається Pile B. Оскільки ви зробили обмін у вісім базових, напишіть 13 як базову вісім числівників на просторі, передбаченому для купи B нижче. Щоб додати, просто об'єднайте блоки з Pile A і Pile B, щоб сформувати одну велику купу блоків. Ви формуєте об'єднання палі A і ворсу B! Зробіть всі можливі обміни з базовими вісьмома блоками, а потім напишіть кількість одиниць у комбінованій купі як основу вісім числівників на просторі, наданому нижче.
Поєднання двох паль таке ж, як і формування суми двох числівників. Ви тільки що додали два числа разом в іншій базі.
Нижче наведено проблему додавання, яку ви щойно виконали в Base Eight.
____________ + _____________ = ____________
Ворс A Ворс B Комбінований ворс
Напишіть шість завдань додавання з вправ 6 -11 у вертикальному форматі, як у базовій шістці, показаному нижче. Вивчіть цю задачу Base Six, а також всі шість завдань з попередніх шести вправ. Спробуйте придумати спосіб вирішення проблем додавання за допомогою паперу та олівця, а не за допомогою базових блоків. Іншими словами, спробуйте придумати свій алгоритм (метод) для виконання додавання в інших базах. Поясніть свій метод і покажіть кілька прикладів. У наступному наборі вправ ви будете вивчати алгоритми додавання.
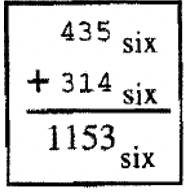
Нехай m < b і n < b. Давайте визначимо слово «доповнення» числа\(m_{b}\), в заданій базі b, щоб бути числом\(n_{b}\), таким\(m_{b} + n_{b} = 10_{b}\). (Не читайте 10b як «десять, база b»). Іншими словами, подумайте про mb як кількість одиничних одиниць менше основи, b Тоді доповненням, n b, буде кількість одиничних одиниць, які потрібно додати до m b таким чином, що сума m b і n b можна було б торгувати рівно один довго. Примітка: Доповнення, як визначено тут, не має нічого спільного зі словом доповнення, як ми визначили та використовували його в теорії наборів! Приклади на наступній сторінці повинні пояснити це визначення.
Ось кілька прикладів доповнень. Основа повинна бути вказана.
У базовій десятці: 3 і 7 є доповненнями, оскільки 3 + 7 = 10
4 і 6 є доповненнями, оскільки 4 + 6 = 10
8 є доповненням 2, так як 8 + 2 = 10
5 є доповненням 5, так як 5 + 5 = 10
У базовій вісімці: доповнення\(5_{\text{eight}}\) становить 3,\(_{\text{eight}}\) оскільки 5\(_{\text{eight}}\) + 3\(_{\text{eight}}\) = 10\(_{\text{eight}}\)
4\(_{\text{eight}}\) і 4\(_{\text{eight}}\) є доповненнями, оскільки 4\(_{\text{eight}}\) + 4\(_{\text{eight}}\) = 10\(_{\text{eight}}\)
2\(_{\text{eight}}\) і 6\(_{\text{eight}}\) є доповненнями, оскільки 2\(_{\text{eight}}\) + 6\(_{\text{eight}}\) = 10\(_{\text{eight}}\)
7\(_{\text{eight}}\) є доповненням 1,\(_{\text{eight}}\) так як 7\(_{\text{eight}}\) + 1\(_{\text{eight}}\) = 10\(_{\text{eight}}\)
Напишіть доповнення кожного числа:
| а.\(7_{\text{nine}}\) | б.\(5_{\text{seven}}\) | c.\(2_{\text{tweleve}}\) |
| д.\(3_{\text{eleven}}\) | е.\(2_{\text{six}}\) | ф.\(1_{\text{two}}\) |
| г.\(2_{\text{three}}\) | ч.\(1_{\text{four}}\) | я.\(3_{\text{five}}\) |
Хоча не обов'язково свідомі зусилля, багато людей використовують доповнення та асоціативну властивість додавання додавати. Наприклад, деякі люди використовують наступну стратегію для додавання в базову десятку. Припустимо, проблема полягала в тому, щоб додати 8 і 6. Людина може подумати: «У мене є 8, і потрібно лише 2 більше, щоб дістатися до 10. Якщо я беру 2 з 6 і додаю його до 8, то у мене є 10 + 4, що дорівнює 14" Іншими словами, завдання 8 + 6 стає 8 + (2 + 4) = (8 + 2) + 4 = 10 + 4 = 14. Звичайно, вони роблять це більш автоматично, ніж це виглядає при записі.
Такий же тип стратегії може бути використаний і в інших базах. Вивчіть наступні приклади. Це може допомогти, якщо ви використовуєте одиниці та лонги в базових блоках.
\(4_{\text{nine}} + 8_{\text{nine}} = 4_{\text{nine}} + (5_{\text{nine}} + 3_{\text{nine}}\))
= (\(4_{\text{nine}} + 5_{\text{nine}}) + 3_{\text{nine}}\)
=\(10_{\text{nine}} + 3_{\text{nine}}\)
=\(13_{\text{nine}}\) (що становить 1 довгий і 3 одиниці в базовій дев'ятці)
\(T_{\text{twelve}} + 9_{\text{twelve}} = T_{\text{twelve}} + (2_{\text{twelve}} + 7_{\text{twelve}}\))
= (\(T_{\text{twelve}} + 2_{\text{twelve}}) + 7_{\text{twelve}}\)
=\(10_{\text{twelve}} + 7_{\text{twelve}}\)
=\(17_{\text{twelve}}\) (що становить 1 довгий і 7 одиниць у базі дванадцяти)
\(4_{\text{six}} + 4_{\text{six}} = 4_{\text{six}} + (2_{\text{six}} + 2_{\text{six}}\))
= (\(4_{\text{six}} + 2_{\text{six}}) + 2_{\text{six}}\)
=\(10_{\text{six}} + 2_{\text{six}}\)
=\(12_{\text{six}}\) (що становить 1 довгий і 2 одиниці в базовій шести)
Використовуйте базові блоки або визначення доповнень, щоб виконати такі проблеми додавання:
| а.\(7_{\text{eleven}} + 8_{\text{eleven}}\) | б.\(4_{\text{five}} + 3_{\text{five}}\) |
| c.\(2_{\text{eight}} + 7_{\text{eight}}\) | д.\(9_{\text{thirteen}} + 5_{\text{thirteen}}\) |
| е.\(3_{\text{four}} + 3_{\text{four}}\) | ф.\(6_{\text{seven}} + 4_{\text{seven}}\) |
| г.\(2_{\text{three}} + 2_{\text{three}}\) = | ч.\(1_{\text{two}} + 1_{\text{two}}\) |
| я.\(3_{\text{six}} + 5_{\text{six}}\) | Дж.\(7_{\text{nine}} + 5_{\text{nine}}\) |
Тепер, коли ви можете додавати однозначні числа в будь-яку базу, ви можете складати таблиці додавання. Нижче наведені таблиці додавання в базовій п'ятій та базовій вісімці. Оскільки Base Five має п'ять цифр, її таблиця додавання повинна бути сіткою п'ять на п'ять, а оскільки Base Eight має вісім цифр, її таблиця додавання повинна бути сіткою вісім на вісім. Зверніть увагу, як симетрія, комутативна властивість і властивість, що x + 0 = x для всіх х робить більшу частину таблиці легко заповнити. При складанні таблиць додавання (а пізніше при складанні таблиць множення) в різних базах слід позначити, що це за таблиця. Якщо ви це зробите, то умовність буде полягати в тому, що не потрібно виписувати слово, за якою основою воно знаходиться праворуч від кожного числівника.
Таблиця\(\PageIndex{1}\): Таблиця додавання п'яти базових
| + | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 10 |
| 2 | 2 | 3 | 4 | 10 | 11 |
| 3 | 3 | 4 | 10 | 11 | 12 |
| 4 | 4 | 10 | 11 | 12 | 13 |
Таблиця\(\PageIndex{2}\): Таблиця додавання вісім базових
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Складіть таблиці додавання в зазначену базу.
| а. базова таблиця з трьома додаванням |
| b. таблиця додавання шести базових |
| c Базова таблиця додавання двох |
