2.2: Системи нумерації
- Page ID
- 66885
У цьому наборі вправ ви дізнаєтеся про дві стародавні системи числення - китайці та майя.
Китайські цифри
Китайські числівники використовуються і сьогодні. Символи для деяких китайських числівників наведені нижче.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 100 | 1 000 |
 |
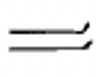 |
 |
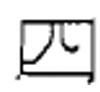 |
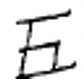 |
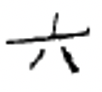 |
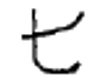 |
 |
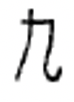 |
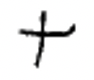 |
 |
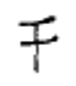 |
Китайські цифри формуються шляхом написання символів по вертикалі і використання мультиплікативного принципу, що спрощує запис числівників за рахунок виключення повторення символів. Наприклад, китайці пишуть числівник для 3,058, думаючи\(3 \times 1000 + 5 \times 10 + 8\) і запишіть символи 3, 1000, 5, 10 і 8 в такому порядку, щоб представити це число. Незважаючи на те, що ви можете думати про 8 як\(8 \times 1\), 1 не записано. Ця китайська цифра (3,058) показана зліва. Справа показана китайська цифра для 872.
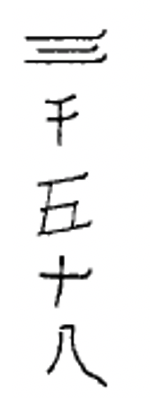
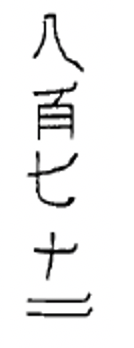
Нижче наведено ще кілька китайських числівників. Переконайтеся, що ви розумієте, як читати всі з них, перш ніж пробувати вправи.
| 6 400 | 87 | 9 531 | 2 605 | 4 011 | 7 000 |
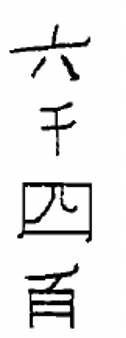 |
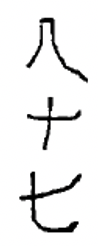 |
 |
 |
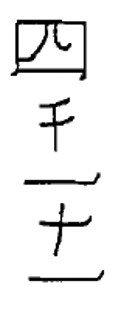 |
 |
Напишіть кожну індуїстсько-арабську цифру як китайську цифру.
- 5 093
- 610
- 427
- 8 008
Таким чином, вам не доведеться продовжувати повертатися назад сторінку, щоб запам'ятати ці символи, ось знову китайські цифри ви, ймовірно, потрібно подивитися на, щоб зробити наступну вправу.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 100 | 1000 |
 |
 |
 |
 |
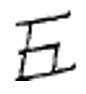 |
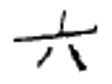 |
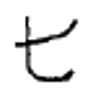 |
 |
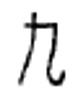 |
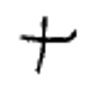 |
 |
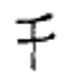 |
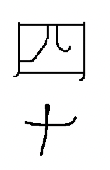
Перепишіть кожну китайську цифру індуї-арабською цифрою.
| а. ____ | б. ____ | c. ____ | д. ____ | е. ____ |
 |
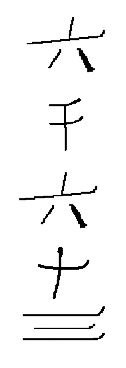 |
 |
 |
 |
Зверніть увагу в китайській системі, що числа більше дев'яти мають символи, написані парами. Щоб написати 800, необхідно написати символ на 8 над символом на 100. ВАЖЛИВЕ ЗАУВАЖЕННЯ: Це вірно, навіть якщо у значенні місця є лише «1", див. 2d вище. Ви ПОВИННІ пам'ятати, щоб написати символ «один» над символом для «десятка»! Хоча мультиплікативний принцип дозволяє записати менше символів, ніж проста адитивна система (принаймні для більшості числівників), подальше спрощення дозволило б нам пропустити написання другого числівника кожної пари. Це спрацювало б, якби ми використовували позицію символу для позначення розміру цієї групи (10, 100, 1000 тощо) Цей тип системи називається позиційною системою числення. Для того, щоб відстежувати позицію, де не використовується цифра, необхідний символ для нуля. Хоча китайська система не потребує символу для нуля, коло було введено, щоб представляти нуль у 1200.
Числівники майя
Остаточна система, про яку ми дізнаємося в цьому наборі вправ, використовує позиційну систему і схожа на китайську систему тим, що символи для числівників пишуться зверху вниз. Числівники майя були розроблені майя жерці південної Мексики і Центральної Америки близько 300 до н.е. Вважається, що це найдавніша позиційна система числення, що включає нуль і використовує його для заповнювача.
Деякі числівники майя наведені нижче. Спробуйте розібратися з викрійкою і потім заповнити відсутні цифри.
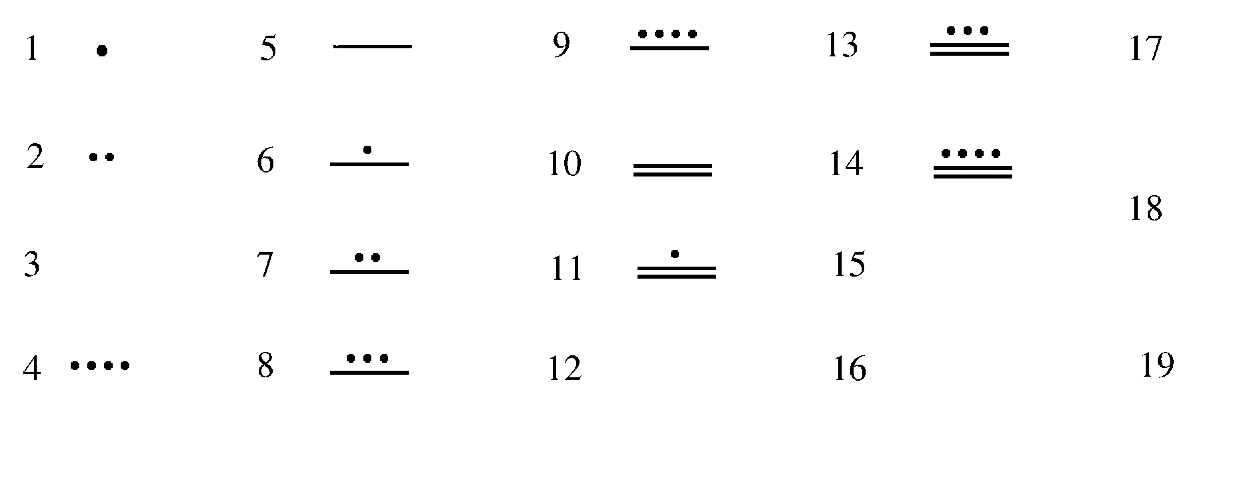
Поясніть, які символи є в цій системі, що вони означають і як система працює для принаймні числівників від одного до дев'ятнадцяти.
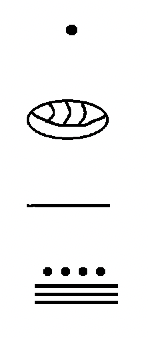
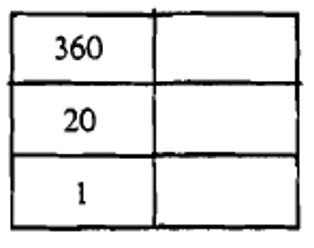
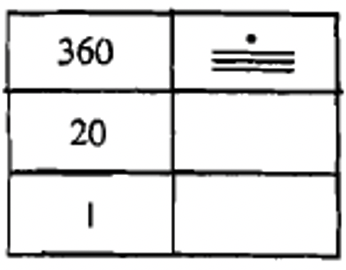
З того, що ви бачили в цій системі досі, це може виглядати як проста адитивна система. Можна здогадатися, що цифра для 20 буде чотири відрізки лінії і що цифра для 103 буде двадцять відрізків лінії і три точки. На перший погляд вона дуже схожа на систему підрахунку. Однак майя використовували вертикальну позиційну систему. Нижній рівень представляв, скільки одиниць (або одиниць), другий рівень вгору представляв, скільки 20-х років, третій рівень вгору представляв скільки 360 (20 18), четвертий рівень вгору представляв скільки 7200 (20 18 20), п'ятий рівень вгору представляв скільки 144,000 (20 18 20) і т.д. крім другого і третього рівня, кожне місце значення збільшується кратним 20. Це майже система Base Twenty, за винятком того дивного третього рівня. Чому третій рівень в 18 разів перевищує другий рівень, пояснюється пізніше. Дивлячись на діаграму зліва, яка показує перші чотири значення місця, може допомогти вам зрозуміти систему.
| 7200-х |
| 360-е |
| 20-х |
| 1-х |
Щоб спробувати зрозуміти все це, ми розглянемо деякі числівники майя, які зараз мають більше однієї позиції. Цифри від одного до дев'ятнадцяти використовують лише нижній рівень, тому не очевидно, що система майя є позиційною, поки ви не порахуєте минуле дев'ятнадцять.
Зліва - дворівневий числівник майя. У нижньому рівні є 16, що представляє 16 одиниць, або 16 (\(16 \times 1\)), плюс є 7 на другому рівні вгору, що представляє 7 груп по двадцять, або 140 (\(7 \times 20\)). Ми додаємо значення кожного рівня, 16 + 140, тому цифра, яку ви бачите, представляє 156.
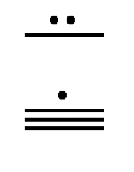
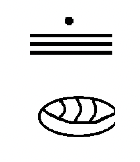
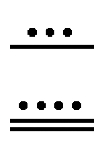
До цих пір ви бачили два основні символи в цій системі - точка (), яка представляє номер один і відрізок лінії (), який представляє число п'ять. Як згадувалося раніше, повинен бути символ для нуля, щоб включити використання значення місця. Для цього майя використовували оболонку, яка виглядала приблизно так:
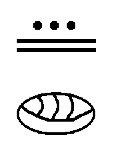
Зліва - дворівнева цифра майя з нулем у нижньому рівні, що представляє нульові одиниці, або 0, плюс 13 на другому рівні вгору, що представляє 13 груп по двадцять, або 260 (\(13 \times 20\)). Таким чином, після додавання значень разом (0 + 260), цифра, яку ви бачите, являє собою число 260.
Створіть індуїстсько-арабський еквівалент кожної цифри майя. Покажіть, як ви отримали відповіді. Зверніть увагу, що між кожним значенням місця слід залишати належний простір. В іншому випадку хтось може неправильно зробити висновок, що число, показане для 5a, представляє 14, що було б відповіддю, якщо не було місця.
| а. ____ | б. ____ | c. ____ |
 |
 |
 |
Тепер, ми будемо йти на деякі три і чотири рівня майя числівник. Пам'ятайте, що значення місця для третього рівня вгору дорівнює 360, а значення місця для четвертого рівня вгору - 7200. Подивіться, чи зможете ви розібратися в них самостійно.
| а. ____ | б. ____ | c. ____ | д. ____ | е. ____ |
 |
 |
 |
 |
 |
Як ви це зробили? Переконайтеся, що якщо у вас все ще виникли проблеми з розумінням будь-якого з них, ви повернетеся і знову працюєте через них.
Це трохи складніше, щоб почати з індуїстсько-арабської цифри і перетворити його на майя, але з трохи терпіння і практики, ви будете робити це швидко і точно! Перш ніж показати метод для цього, спробуйте виконати наступну вправу. Підказка: Це повинно бути легко, а не важко - калькулятор не потрібно. Подумайте про значення місця різних рівнів в системі майя.
Напишіть еквіваленти числівників майя для кожного з наступних чисел:
| а. 1 | б. 20 | c. 360 | д. 7200 | д. 144000 |
Щоб перетворити число на числівник майя, перше, що вам доведеться визначити, скільки рівнів буде мати числівник. Запам'ятайте рівні: 1, 20, 360, 7200, 144000, 2880000 тощо Таким чином, будь-яка цифра менше 20 має один рівень, цифра між 20 і 359 має два рівні, цифра між 360 і 7199 має три рівні, цифра між 7200 і 143999 має чотири рівні, і так далі.
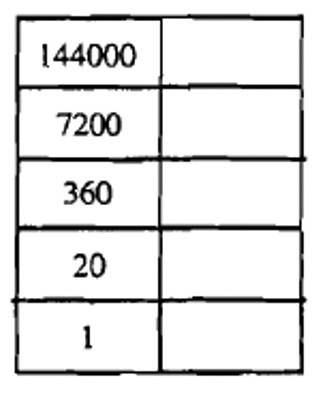
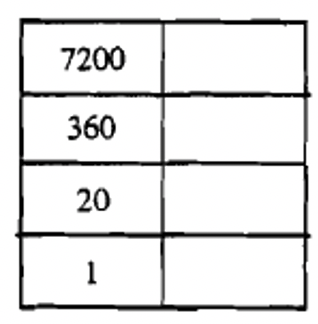
Це може допомогти, якщо ви створите таблицю з правильною кількістю рівнів, встановлених вже з пробілом, щоб заповнити символ, який ви будете використовувати на кожному рівні. Наприклад, подивіться нижче на чотири найпоширеніші діаграми, які ви будете використовувати.
 |
 |
 |
 |
Почнемо з числа 174. Переконайте себе, що це буде дворівневий числівник. Ми почнемо у верхній частині, яка є 20 місце значення. Ми повинні запитати себе, скільки 20-х років у 174? Це питання поділу:\(174 \div 20 = 8\), залишок 14. Ми можемо почати будувати числівник майя, починаючи з дворівневої діаграми і заповнивши 8 на другому рівні вгору, як показано нижче.
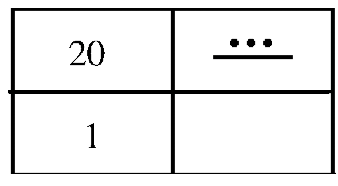
Поки що у нас є вісім груп по двадцять, або 160 заповнених, що залишає ще 14 (решту) для розміщення. Коли ви спускаєтеся до місця одиниць, залишок заповнюється туди. Отже, наступним кроком є заповнення 14 в місці одиниць. Зробіть це на вакантному місці на показаній схемі. Перш ніж відчувати себе задоволеним, що все правильно, перевірте свою відповідь, обчисливши щойно побудовану вами цифру майя і подивіться, чи справді це 174. Потім позбудьтеся від діаграми і напишіть відповідь як числівник майя, як показано праворуч.
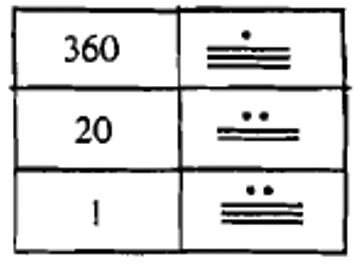
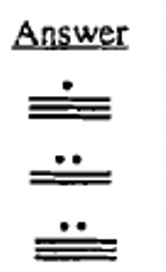
Спробуємо інший номер. Ми перетворимо 6017 в числівник майя. Це буде трирівнева цифра, тому ми почнемо з трирівневої діаграми і з'ясувати, скільки 360 в 6017. Робимо таку задачу поділу:\(6017 \div 360 = 16\), залишок 257. Це говорить нам поставити символ для 16 на третьому рівні вгору (360-е місце). Тепер нам належить взяти залишок, 257, і з'ясувати, скільки 20-х в ньому є, щоб дізнатися, що поставити на другому рівні. Робимо таку задачу поділу:\(257 \div 20 = 12\), залишок 17. Оскільки залишилося лише значення місця одиниць (нижній рівень), решта 17 йде на цьому рівні. Послідовність заповнення графіків наведена нижче. Переконайтеся, що ви повернетеся назад і перевірити свою роботу, перетворивши цифру назад в індуї-арабську (\(1 \times 17 + 12 \times 20 + 16 \times 360\)) і побачивши, чи дійсно вона дорівнює 6017.
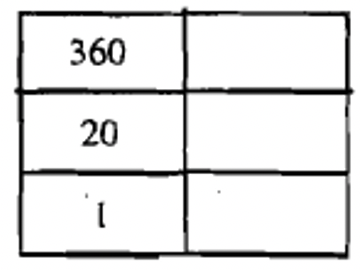 |
 |
 |
 |
Перш ніж продовжувати, Я збираюся показати вам швидкий і простий спосіб дізнатися частку і залишок за допомогою простого калькулятора при виконанні цих проблем поділу. Якщо ви вже можете зробити це легко або ваш калькулятор з'ясовує це для вас, перейдіть до вправи 8. Припустимо, ви збиралися змінити число 5263 на майя. Перша проблема поділу, яку вам доведеться обчислити, буде\(5263 \div 360\). Коли ви робите це на калькуляторі, він показує щось на зразок 14.619444. Це вказує на те, що в 5263 є 14 360, але решта не очевидна. Принаймні, ви знаєте, щоб поставити 14 на третьому рівні вгору. Щоб знайти залишок на калькуляторі, введіть 14 360 - 5263 і число, що показує залишок, якщо ви ігноруєте негативний знак! В даному випадку залишок дорівнює 223. Пам'ятайте, що залишок повинен бути меншим за те, що ви спочатку розділили на —менше 360 у цьому випадку. Якщо ви хотіли знайти, що поставити на місце 20, ви б повторили цей процес, взявши 223 (решту) і розділивши його на 20. Можливо, вам не знадобиться калькулятор для продовження. Спробуємо знайти частку і залишок при діленні 24567 на 7200. На калькуляторі,\(24567 \div 7200 = 3.4120833...\) Таким чином, частка 3. Щоб отримати залишок, ключ в\(3 \times 7200 - 24567\), який дає залишок 2967 (що менше 7200!). Таким чином, відповідь 3, решта 2967. Для перевірки, 7200 3 + 2967 повинні дорівнювати 24567. Подумайте, чому цей процес працює, і спробуйте його на наступних кількох проблемах.
Використовуйте калькулятор, щоб знайти частку та залишок для цих задач ділення.
- \(9876 \div 360\)= ____
- \(71509 \div 7200\)= ____
- \(333 \div 20\)= ____
- \(430040 \div 144000\)= ____
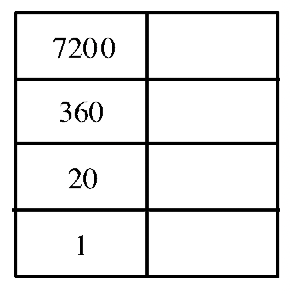
Давайте перетворимо 71509 в майя. Заповніть символи майя на графіку ліворуч, коли ми працюємо над проблемою. Це чотирирівневий числівник майя і вправа 8b повинні допомогти нам розпочати роботу! Ви отримали 9, решту 6709? Таким чином, 9 знаходиться на четвертому рівні вгору. Тепер обчислюємо:\(6709 \div 360 = 18\), залишок 229. Таким чином, 18 знаходиться на третьому рівні вгору. Наступне обчислення:\(229 \div 20 = 11\), решта 9, так що 11 - другий рівень вгору, і що залишає 9 на місці одиниць. Остаточна відповідь показана праворуч.
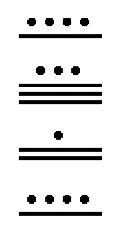

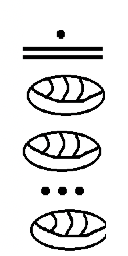
Ну, яке число ми повинні перетворити зараз? Як щодо 430040, щоб ми могли скористатися допомогою вправи 8d? Заповніть символи майя на графіку ліворуч, коли ми працюємо над проблемою. Спочатку зауважимо, що це п'ятирівневий числівник майя, і тому ми робимо поділ у вправі 8d, який дає 2 на п'ятому рівні вгору з залишком 142040. Це великий залишок, але менше 144000. Тепер ми ділимо 142040 на 7200, щоб отримати 19 на четвертому рівні вгору і залишок 5240. Далі розділіть 5240 на 360, щоб отримати 14 на третьому рівні вгору і залишок 200. Є рівно десять 20 в 200 і немає залишку для одиниць, тому нам потрібно мати нуль на нижньому рівні. Нарешті, числівник, який ми шукаємо, показано праворуч. Переконайтеся, що ви перевіряєте це шляхом обчислення\(2 \times 144000 + 19 7200 + 14 \times 360 + 10 \times 20 + 0!\) Чи дійсно він дорівнює 430040? Якщо так, то це правильно.

Давайте перетворимо 1584060 в майя. Це ще п'ятирівневий числівник майя, тому наш перший поділ\(1584060 \div 144000\) дає нам 11 на п'ятому рівні вгору з залишком 60. У 60 немає 7200 або 360, тому на цих двох рівнях повинні бути нулі. Є 3 20 в 60 без залишку, тому рівень одиниць також повинен мати нуль. Справа зображено числівник. Будь ласка, перевірте це. Це насправді 1584060?
Подумайте про найвищому числівниковому значенні, яке може бути на будь-якому заданому рівні. Наприклад, нижній рівень може піднятися до 19, або. Але як щодо другого рівня вгору? Яке число було б представлено дворівневим числівником майя, якби на другому рівні було 19 вгору і нуль на нижньому рівні? Напишіть числівник майя для 380.
Яке найвище значення числівника майя, яке повинно бути на другому рівні вгору? Що є найвищим символом майя, який може бути на будь-якому рівні, крім другого рівня вгору?
Перетворіть кожне з наступних числівників майя. (показати роботу) ПЕРЕВІРИТИ Відповіді!
- 1549
- 4750
- 53981
- 145804
- 1000000
Можливо, вам буде цікаво, чому майя вибрали 360 для третього рівня вгору замість 400, що здається більш природним. Їх система підрахунку базувалася на їх календарі, який складався з 18 місяців по 20 днів кожен, отже 360. Зайві п'ять днів вважалися «марними», і вони не переживали за них. Їх система дозволила легко підрахувати час. Вони не вважали «марні дні». Наприклад, розглянемо наступне:
| a. 1 рік | б. 2 роки | c. 3 роки | c. 5 місяців, 9 днів | d. 8 років, 11 місяців |
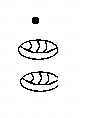 |
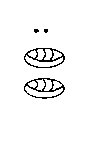 |
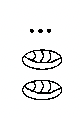 |
 |
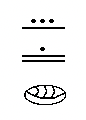 |
Напишіть числівник майя за кількістю (немарних) днів в:
- 7 місяців, 15 днів
- 13 років майя
- 20 років майя
Завершальним вправою цього набору буде порівняння індуїстсько-арабських, китайських і майянських цифр.
Вкажіть, скільки різних символів людина повинна запам'ятати, щоб зрозуміти кожну систему:
- Індуї-Арабська: _____
- Китайська: _____
- Майя: _____
Напишіть кожне число як числівник китайською мовою та майя. Зверніть увагу, скільки символів потрібно, щоб написати дане число в індуї-арабською, китайською та майя. Показати роботу.
- 15
- 100
- 100
- 9999
