6.5: Співпраця

Ферменти та інші білкові комплекси можуть мати кілька місць зв'язування, і коли субстрат зв'язується з одним з цих ділянок, інші ділянки можуть активізуватися. Добре вивчений приклад - зв'язування молекули кисню з білком гемлобін. Гемоглобін може зв'язувати чотири молекули$\mathrm{O}_{2}$, а коли три молекули пов'язані, четверта молекула має підвищену спорідненість до зв'язування. Ми називаємо це співробітництвом.

Ми будемо моделювати кооперативність, припускаючи, що фермент має два розділених, але невиразних місця зв'язування для субстрату$S$. Наприклад, фермент може

Малюнок 6.4: Кооперативність.

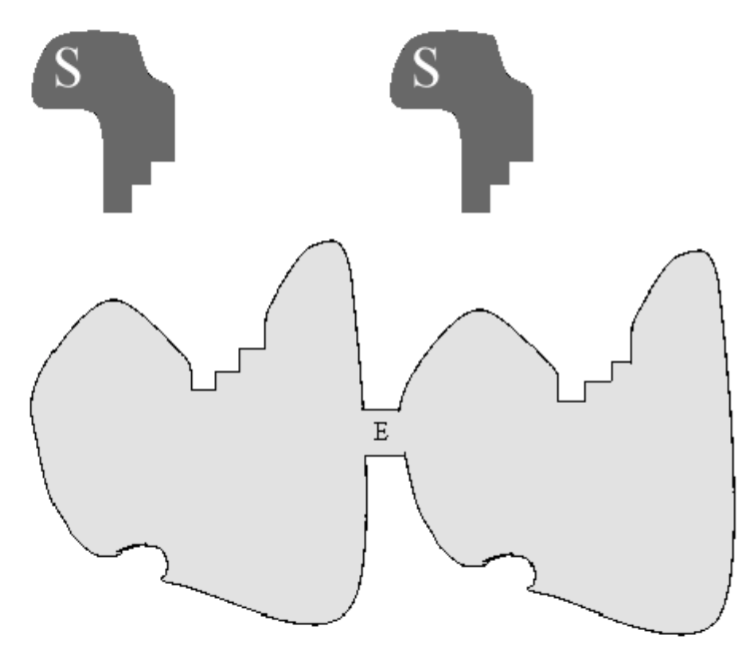
бути білковим димером, що складається з двох однакових субпротеїнів з однаковими місцями зв'язування для$S$. Мультфільм цього ферменту показаний на рис.6.4. Оскільки два місця зв'язування не відрізняються, нам потрібно розглянути тільки два комплекси:$C_{1}$ і, з ферментом$C_{2}$, пов'язаним з однією або двома молекулами субстрату відповідно. Коли фермент проявляє кооперативність, зв'язування другої молекули субстрату має більшу константу швидкості, ніж зв'язування першої. Тому ми розглядаємо наступну реакцію:

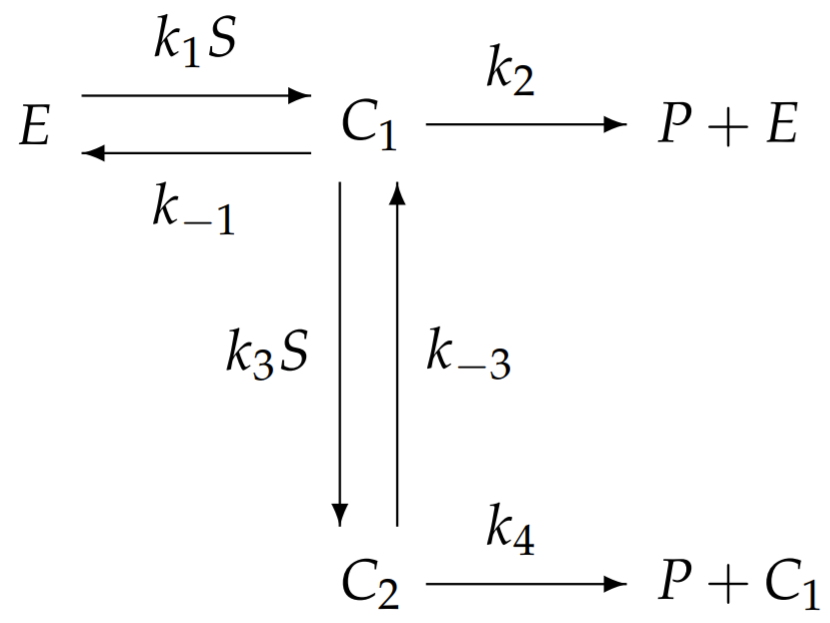
де кооперативність передбачає це$k_{1} \ll k_{3}$. Застосування закону масового позову призводить до

$$\begin{aligned} \frac{d C_{1}}{d t} &=k_{1} S E+\left(k_{-3}+k_{4}\right) C_{2}-\left(k_{-1}+k_{2}+k_{3} S\right) C_{1} \\[4pt] \frac{d C_{2}}{d t} &=k_{3} S C_{1}-\left(k_{-3}+k_{4}\right) C_{2} \end{aligned} \nonumber$$

Застосування квазірівноважного наближення$\dot{C}_{1}=\dot{C}_{2}=0$ та закону збереження$E_{0}=E+C_{1}+C_{2}$ призводить до отримання наступної системи двох рівнянь і двох невідомих:

$$\begin{align} \left(k_{-1}+k_{2}+\left(k_{1}+k_{3}\right) S\right) C_{1}-\left(k_{-3}+k_{4}-k_{1} S\right) C_{2} &=k_{1} E_{0} S, \\[4pt] k_{3} S C_{1}-\left(k_{-3}+k_{4}\right) C_{2} &=0 . \end{align} \nonumber$$

Ділимо$(6.5.1)$ на$k_{1}$ і$(6.5.2)$ на$k_{3}$ і визначаємо

$$K_{1}=\frac{k_{-1}+k_{2}}{k_{1}}, \quad K_{2}=\frac{k_{-3}+k_{4}}{k_{3}}, \quad \epsilon=k_{1} / k_{3} \nonumber$$

для отримання

$$\begin{align} \left(\epsilon K_{1}+(1+\epsilon) S\right) C_{1}-\left(K_{2}-\epsilon S\right) C_{2} &=\epsilon E_{0} S, \\[4pt] S C_{1}-K_{2} C_{2} &=0 . \end{align} \nonumber$$

Ми можемо відняти (6.5.5) з (6.5.4) і скасувати$\epsilon$, щоб отримати

$$\left(K_{1}+S\right) C_{1}+S C_{2}=E_{0} S . \nonumber$$

Рівняння (6.5.5) і (6.5.6) можуть бути вирішені для$C_{1}$ і$C_{2}$:

$$\begin{align} C_{1} &=\frac{K_{2} E_{0} S}{K_{1} K_{2}+K_{2} S+S^{2}} \\[4pt] C_{2} &=\frac{E_{0} S^{2}}{K_{1} K_{2}+K_{2} S+S^{2}} \end{align} \nonumber$$

так що швидкість реакції задається

$$\begin{align} \frac{d P}{d t} &=k_{2} C_{1}+k_{4} C_{2} \\[4pt] &=\frac{\left(k_{2} K_{2}+k_{4} S\right) E_{0} S}{K_{1} K_{2}+K_{2} S+S^{2}} \end{align} \nonumber$$

Щоб висвітлити цей результат, ми розглянемо два обмежувальних випадки: (i) відсутність кооперативності, де активні ділянки діють незалежно, так що кожен білковий димер, скажімо, можна розглядати як два незалежних білкових мономера; (ii) сильна кооперативність, де зв'язування другого субстрату має набагато більшу постійну швидкість ніж прив'язка першого.

Незалежні активні сайти

Малюнок 6.5: Швидкість реакції$d P / d t$ як функція субстрату$S$. Показані розв'язки рівняння Хілла з$V_{m}=1, K_{m}=1$, і for$n=1,2$.

Тому для самостійних активних ділянок швидкість реакції стає

$$\begin{aligned} \frac{d P}{d t} &=\frac{\left(2 k_{2} K_{m}+2 k_{2} S\right) E_{0} S}{K_{m}^{2}+2 K_{m} S+S^{2}} \\[4pt] &=\frac{2 k_{2} E_{0} S}{K_{m}+S} \end{aligned} \nonumber$$

Швидкість реакції для ферменту димерного білка, що складається з незалежних ідентичних мономерів, просто вдвічі більше, ніж у ферменту мономерного білка, інтуїтивно очевидний результат.

Міцна співпраця

Тепер ми припустимо, що після того, як перший субстрат зв'язується з ферментом, другий субстрат зв'язується набагато легше, так що$k_{1} \ll k_{3}$. Кількість ферментів, пов'язаних з однією молекулою субстрату, повинно бути набагато менше, ніж кількість зв'язаних з двома молекулами субстрату, в результаті чого$C_{1} \ll C_{2}$. Діливши (6.5.7) на (6.5.8), ця нерівність стає

$$\frac{C_{1}}{C_{2}}=\frac{K_{2}}{S} \ll 1 . \nonumber$$

Розділивши чисельник і знаменник$(6.5.9)$ на$S^{2}$, ми маємо

$$\frac{d P}{d t}=\frac{\left(k_{2} K_{2} / S+k_{4}\right) E_{0}}{\left(K_{1} / S\right)\left(K_{2} / S\right)+\left(K_{2} / S\right)+1} . \nonumber$$

Щоб прийняти межу цього виразу як$K_{2} / S \rightarrow 0$, ми встановлюємо$K_{2} / S=0$ скрізь, крім першого члена в знаменнику, оскільки$K_{1} / S$ обернено пропорційний$k_{1}$ і може перейти до нескінченності в цій межі. Взявши межу і помноживши чисельник і знаменник на$S^{2}$,

$$\frac{d P}{d t}=\frac{k_{4} E_{0} S^{2}}{K_{1} K_{2}+S^{2}} \nonumber$$

Тут максимальна швидкість реакції є$V_{m}=k_{4} E_{0}$, а змінена постійна Michaelismenten є$K_{m}=\sqrt{K_{1} K_{2}}$, так що

$$\frac{d P}{d t}=\frac{V_{m} S^{2}}{K_{m}^{2}+S^{2}} \nonumber$$

У біохімії ця швидкість реакції узагальнена до

$$\frac{d P}{d t}=\frac{V_{m} S^{n}}{K_{m}^{n}+S^{n}} \nonumber$$

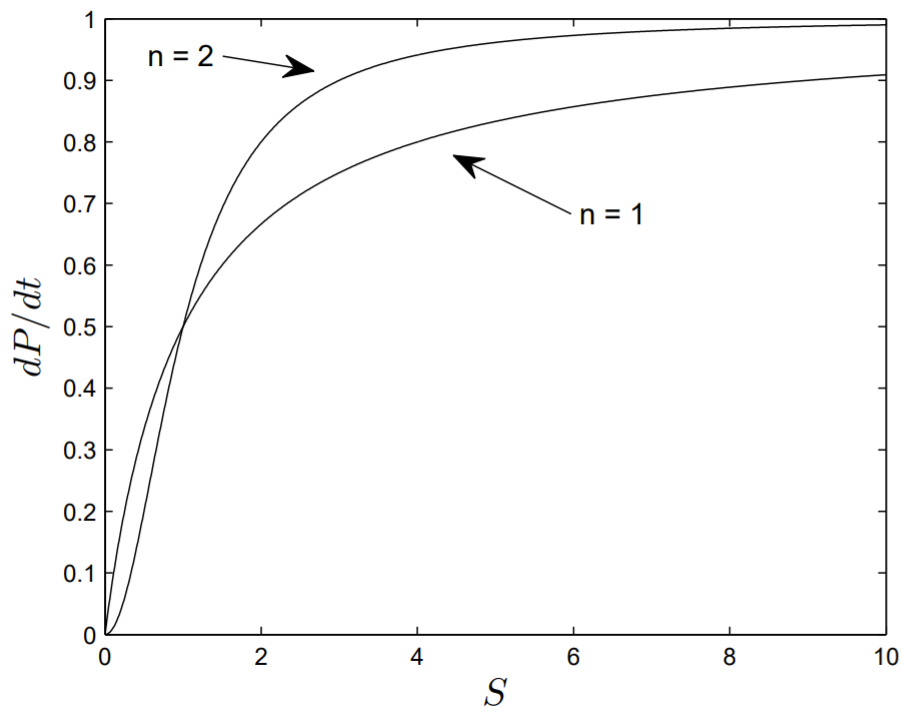
відомий як рівняння Хілла, і шляхом зміни$n$ використовується для підгонки експериментальних даних.

На рис. $6.5$, ми побудували швидкість реакції в$d P / d t$ порівнянні з$S$ отриманою з рівняння Хілла з$n=1$ або 2. При малюванні фігури ми взяли обидва$V_{m}$ і$K_{m}$ рівні одиниці. Видно, що зі$n$ збільшенням швидкості реакції все швидше насичується до свого максимального значення.