6.3: Конкурентне гальмування
- Page ID
- 66702
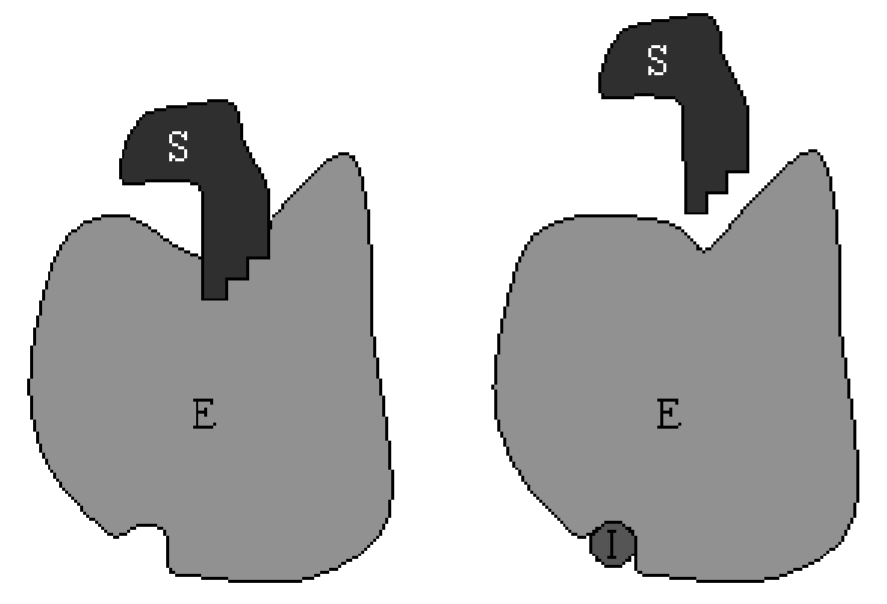
Конкурентне гальмування відбувається, коли молекули інгібіторів конкурують з молекулами субстрату за зв'язування з активною ділянкою того ж ферменту Коли інгібітор зв'язується з ферментом, жоден продукт не виробляється, тому конкурентне інгібування зменшить швидкість реакції. Мультфільм цього процесу показаний на рис. \(6.2\).
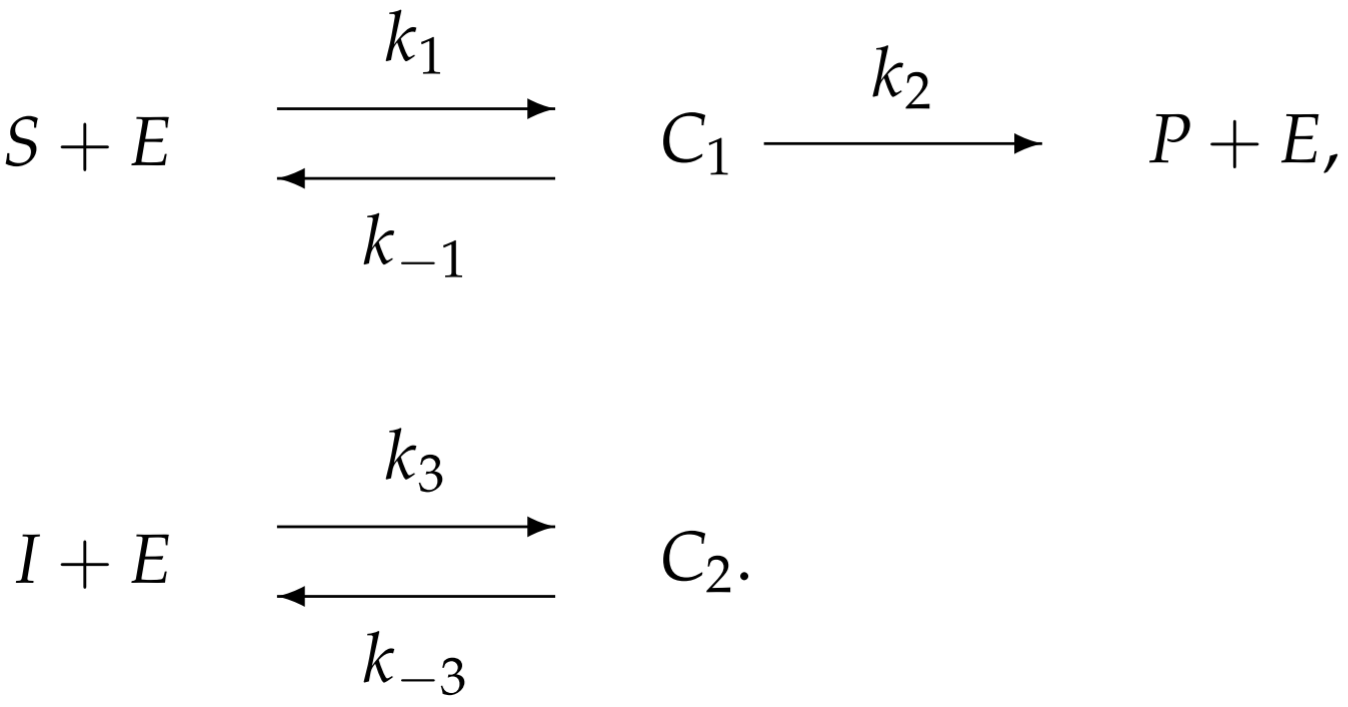
Для моделювання конкурентного інгібування вводимо додаткову реакцію, пов'язану з інгібітор-ферментним зв'язуванням:
При більш складних ферментативних реакціях схема реакції стає важко інтерпретувати. Мабуть, більш простий спосіб візуалізувати реакцію - це наступна перемальована схема:
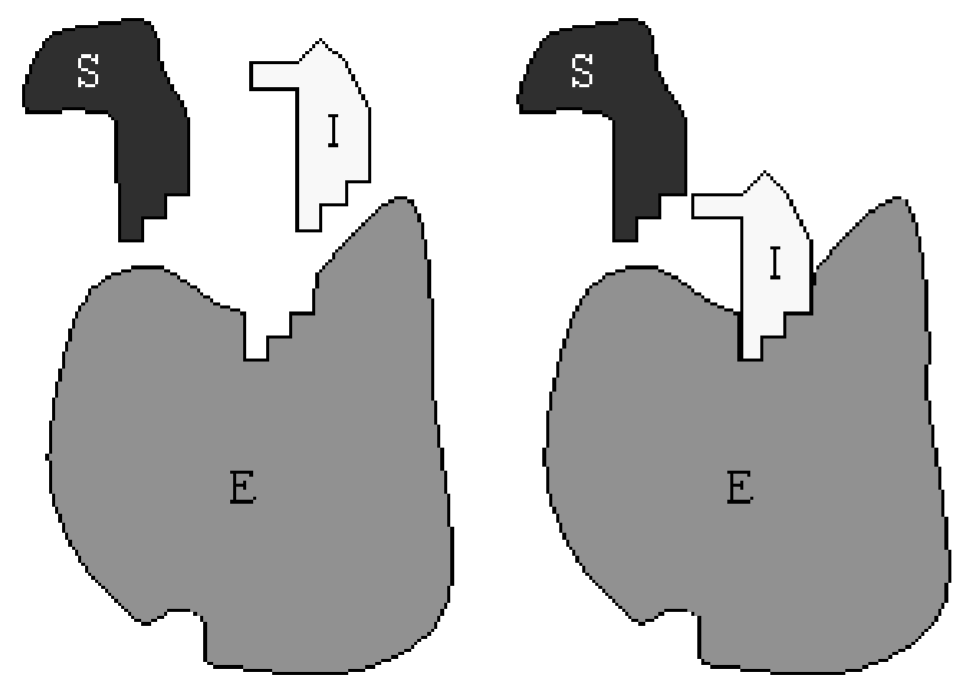
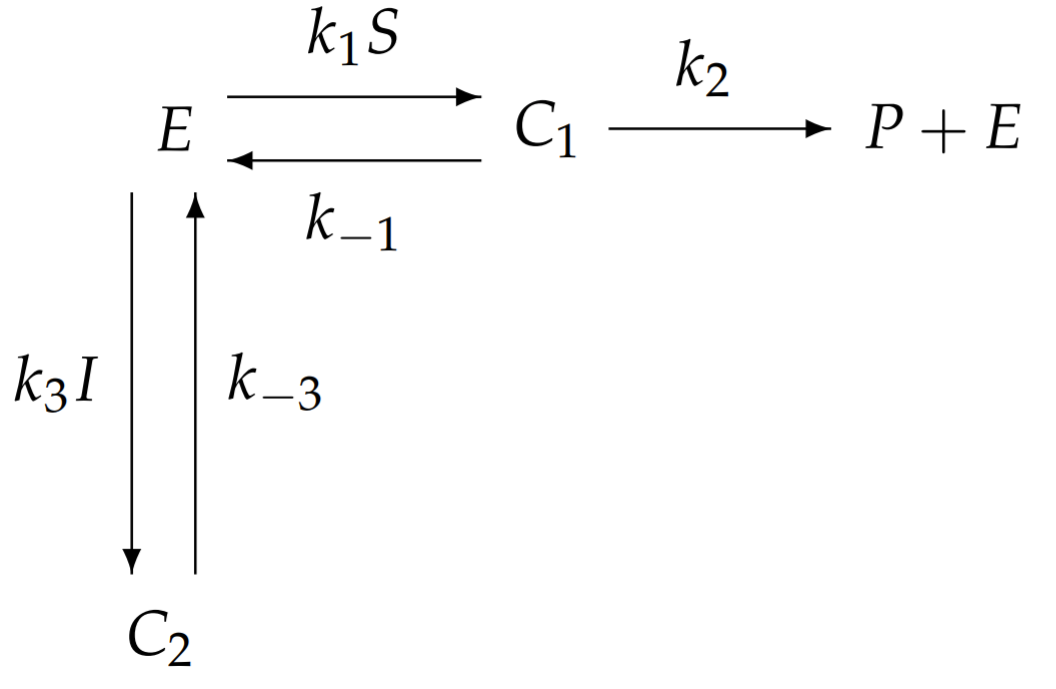
Тут субстрат\(S\) і інгібітор\(I\) поєднуються з відповідними константами швидкості, а не обробляються окремо. З цієї перемальованої схеми відразу видно, що інгібування здійснюється шляхом секвестеризації ферменту у вигляді\(C_{2}\) і запобігання його участі в каталізі\(S\) до\(P\).
Наша мета - визначити швидкість реакції\(\dot{P}\) в перерахунку на концентрації субстрату та інгібітора, а також загальну концентрацію ферменту (вільної та пов'язаної). Закон масової дії, застосований до двох комплексів і продукту призводить до
\[\begin{aligned} \frac{d C_{1}}{d t} &=k_{1} S E-\left(k_{-1}+k_{2}\right) C_{1} \\[4pt] \frac{d C_{2}}{d t} &=k_{3} I E-k_{-3} C_{2} \\[4pt] \frac{d P}{d t} &=k_{2} C_{1} \end{aligned} \nonumber \]
Фермент, вільний і пов'язаний, зберігається так, що
\[\frac{d}{d t}\left(E+C_{1}+C_{2}\right)=0 \quad \Longrightarrow \quad E+C_{1}+C_{2}=E_{0} \quad \Longrightarrow \quad E=E_{0}-C_{1}-C_{2} . \nonumber \]
Під квазірівноважним наближенням\(C_{1}=\dot{C}_{2}=0\), так що
\[\begin{array}{r} k_{1} S\left(E_{0}-C_{1}-C_{2}\right)-\left(k_{-1}+k_{2}\right) C_{1}=0, \\[4pt] k_{3} I\left(E_{0}-C_{1}-C_{2}\right)-k_{-3} C_{2}=0, \end{array} \nonumber \]
в результаті якої утворюється наступна система двох лінійних рівнянь і двох невідомих\(\left(C_{1}\right.\) і\(\left.C_{2}\right)\):
\[\begin{align} \left(k_{-1}+k_{2}+k_{1} S\right) C_{1}+k_{1} S C_{2} &=k_{1} E_{0} S \\[4pt] k_{3} I C_{1}+\left(k_{-3}+k_{3} I\right) C_{2} &=k_{3} E_{0} I \end{align} \nonumber \]
Визначимо постійну Міхаеліса-Ментена,\(K_{m}\) як і раніше, і додаткову константу,\(K_{i}\) пов'язану з реакцією інгібітора:
\[K_{m}=\frac{k_{-1}+k_{2}}{k_{1}}, \quad K_{i}=\frac{k_{-3}}{k_{3}} \nonumber \]
Розподіл\((6.3.2)\) на\(k_{3}\) врожайність\(k_{1}\) і\((6.3.3)\) на
\[\begin{align} \left(K_{m}+S\right) C_{1}+S C_{2} &=E_{0} S \\[4pt] I C_{1}+\left(K_{i}+I\right) C_{2} &=E_{0} I \end{align} \nonumber \]
Оскільки наша мета - отримати швидкість реакції, яка вимагає визначення\(C_{1}\), множимо\((6.3.5)\) на\(\left(K_{i}+I\right)\) і\((6.3.6)\) на\(S\), і віднімаємо:
\[\begin{aligned} \left(K_{m}+S\right)\left(K_{i}+I\right) C_{1}+S\left(K_{i}+I\right) C_{2} &=E_{0}\left(K_{i}+I\right) S \\[4pt] S I C_{1}+S\left(K_{i}+I\right) C_{2} &=E_{0} S I \\[4pt] \left(\left(K_{m}+S\right)\left(K_{i}+I\right)-S I\right) C_{1} &=K_{i} E_{0} S \end{aligned} \nonumber \]
або після скасування та перестановки
\[\begin{aligned} C_{1} &=\frac{K_{i} E_{0} S}{K_{m} K_{i}+K_{i} S+K_{m} I} \\[4pt] &=\frac{E_{0} S}{K_{m}\left(1+I / K_{i}\right)+S} \end{aligned} \nonumber \]
Тому швидкість реакції задається
\[\begin{align} \frac{d P}{d t} &=\frac{\left(k_{2} E_{0}\right) S}{K_{m}\left(1+I / K_{i}\right)+S} \nonumber \\[4pt] &=\frac{V_{m} S}{K_{m}^{\prime}+S} \end{align} \nonumber \]
де
\[V_{m}=k_{2} E_{0}, \quad K_{m}^{\prime}=K_{m}\left(1+I / K_{i}\right) . \nonumber \]
Порівнюючи пригнічену швидкість реакції\((6.3.7)\) і\((6.3.8)\) з розгальмованою швидкістю реакції\((6.2.6)\) і\((6.2.7)\), ми спостерігаємо, що інгібування збільшує константу Міхаеліса-Ментена реакції, але залишає незмінною максимальну реакцію швидкість. Оскільки константа Міхаеліса-Ментена визначається як концентрація субстрату, необхідна для досягнення половини максимальної швидкості реакції, додавання інгібітора з фіксованою концентрацією субстрату діє на зменшення швидкості реакції. Однак реакція, насичена субстратом, все ще досягає розгальмованої максимальної швидкості реакції.