6.4: Аллостеричне гальмування

Last updated
Save as PDF

Page ID: 66701

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Термін аллостерія походить від грецького слова аллос, що означає різні, і стерео, що означає твердий, і відноситься до ферменту з регулюючим зв'язуючим сайтом окремо від його активного вузла зв'язування. У нашій моделі аллостеричного інгібування передбачається, що молекула інгібітора зв'язується зі своїм власним регуляторним сайтом на ферменті, що призводить або до зниженої спорідненості зв'язування субстрату з ферментом, або зниженою швидкістю перетворення субстрату в продукт. Мультфільм аллостеричного гальмування внаслідок зниженої спорідненості зв'язування показаний на рис. $6.3$.

Загалом, нам потрібно визначити три комплекси:$C_{1}$ це комплекс, утворений з субстрату і ферменту;$C_{2}$ з інгібітора і ферменту, і;$C_{3}$ з субстрату, інгібітора і ферменту. Прописуємо хімічні реакції наступним чином:

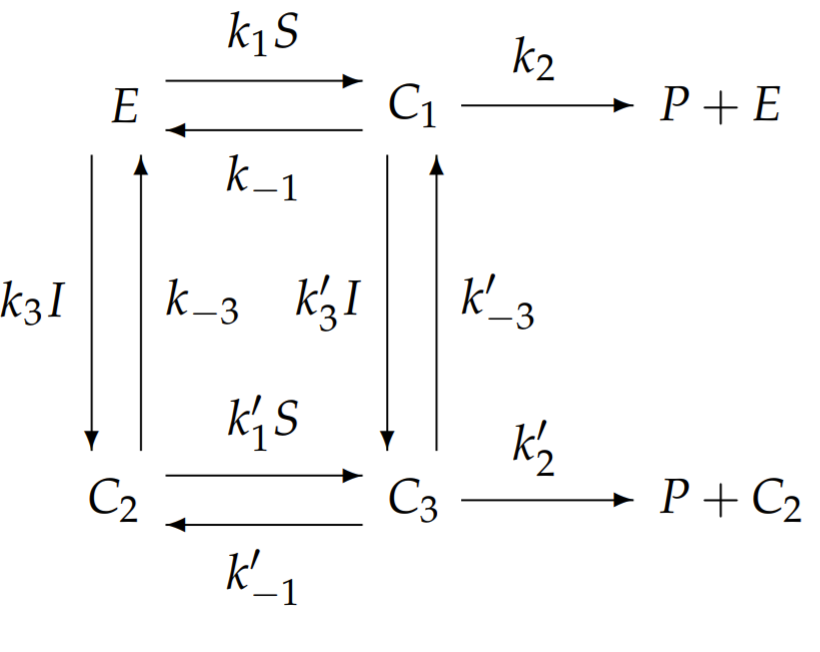
$clipboard_e7c6048933a68c0850cd297b12417b071.png$

Загальна модель аллостеричного інгібування з десятьма незалежними константами швидкості виявляється занадто складною для аналізу. Ми спростимо цю загальну модель до такої з меншою кількістю констант швидкості, яка все ще демонструє унікальні особливості аллостеричного гальмування. Одне можливе, але нецікаве спрощення передбачає, що якщо$I$ зв'язується з$E$, то$S$ ні; однак це зменшує аллостеричне гальмування до конкурентного гальмування і втрачає суть алостерії. Замість цього ми спрощуємо, дозволяючи обидва$I$ і$S$ одночасно зв'язуватися$E$, але ми припускаємо, що зв'язування I запобігає перетворенню субстрату в продукт. З цим спрощенням,$k_{2}^{\prime}=0$. Для подальшого зменшення кількості незалежних констант швидкості припускаємо, що на прив'язку$S$ до$E$ не впливає пов'язана присутність$I$, а на прив'язку$I$ до$E$ не впливає прив'язка наявність$S$. Ці наближення мають на увазі, що всі загрунтовані константи швидкості дорівнюють відповідним негрунтованим константам швидкості$k_{1}^{\prime}=k_{1}$, наприклад, і т.д. з цими спрощеннями схема хімічної реакції спрощує

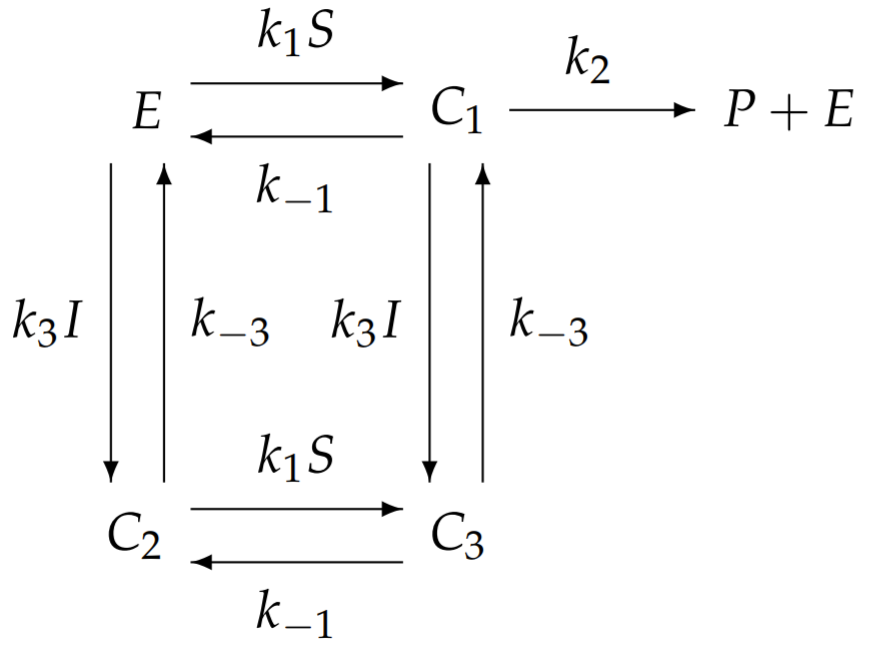
$clipboard_eaf907d6091b64c4a42b2f90c6571d8ac.png$

і зараз існує всього п'ять незалежних констант швидкості. Запишемо рівняння для комплексів, використовуючи закон масової дії:

\[\begin{align} &\frac{d C_{1}}{d t}=k_{1} S E+k_{-3} C_{3}-\left(k_{-1}+k_{2}+k_{3} I\right) C_{1} \\[4pt] &\frac{d C_{2}}{d t}=k_{3} I E+k_{-1} C_{3}-\left(k_{-3}+k_{1} S\right) C_{2} \\[4pt] &\frac{d C_{3}}{d t}=k_{3} I C_{1}+k_{1} S C_{2}-\left(k_{-1}+k_{-3}\right) C_{3} \end{align} \nonumber \]

в той час як швидкість реакції задається

\[\frac{d P}{d t}=k_{2} C_{1} \nonumber \]

Знову ж таки, як вільний, так і зв'язаний фермент зберігається, так що$E=E_{0}-C_{1}-C_{2}-C_{3}$. При квазірівноважному наближенні$\dot{C}_{1}=\dot{C}_{2}=\dot{C}_{3}=0$ ми отримуємо систему з трьох рівнянь і трьох невідомих:$C_{1}, C_{2}$ і$C_{3} .$ незважаючи на наші спрощення, аналітичне рішення швидкості реакції залишається безладним (див. Keener & Sneyd, посилання на кінець глави) і не особливо висвітлює. Опускаємо тут повний аналітичний результат і визначаємо тільки максимальну швидкість реакції.

Максимальна швидкість реакції$V_{m}^{\prime}$ для алостерично-інгібованої реакції визначається як похідна за часом концентрації продукту, коли реакція насичена субстратом; тобто

\[\begin{aligned} V_{m}^{\prime} &=\lim _{S \rightarrow \infty} d P / d t \\[4pt] &=k_{2} \lim _{S \rightarrow \infty} C_{1} \end{aligned} \nonumber \]

При насиченні субстрату кожен фермент буде займати місце зв'язування субстрату. Ферменти або пов'язані тільки з субстратом в комплексі$C_{1}$, або зв'язуються разом з субстратом і інгібітором в комплексі$C_{3}$. Відповідно, схема хімічної реакції з насиченням субстрату спрощує

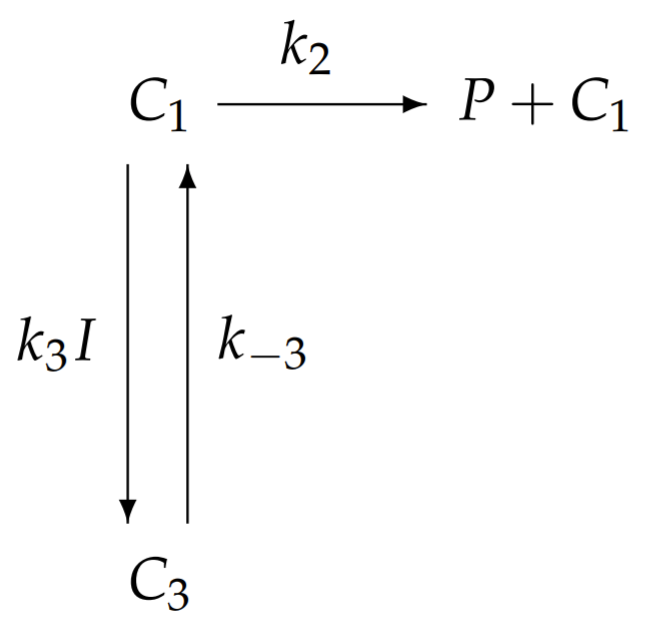
$clipboard_e440294fbb66b8045d534adf265bfc3fd.png$

Рівняння для$C_{1}$ і$C_{3}$ з насиченістю підкладки, таким чином, задаються

\[\begin{align} \frac{d C_{1}}{d t} &=k_{-3} C_{3}-k_{3} I C_{1} \\[4pt] \frac{d C_{3}}{d t} &=k_{3} I C_{1}-k_{-3} C_{3} \end{align} \nonumber \]

а квазірівноважне наближення дає єдине незалежне рівняння

\[\begin{align} \nonumber C_{3} &=\left(k_{3} / k_{-3}\right) I C_{1} \\[4pt] &=\left(I / K_{i}\right) C_{1} \end{align} \nonumber \]

з$K_{i}=k_{-3} / k_{3}$ як раніше. Рівняння, що виражає збереження ферменту, дається шляхом$E_{0}=C_{1}+C_{3}$. Цей закон про збереження, разом з$(6.4.7)$, дозволяє нам вирішувати для$C_{1}$:

\[C_{1}=\frac{E_{0}}{1+I / K_{i}} \nonumber \]

Тому максимальна швидкість реакції для алостерично-інгібованої реакції задається

\[\begin{aligned} V_{m}^{\prime} &=\frac{k_{2} E_{0}}{1+I / K_{i}} \\[4pt] &=\frac{V_{m}}{1+I / K_{i}} \end{aligned} \nonumber \]

де$V_{m}$ максимальна швидкість реакції як розгальмованої, так і конкурентної гальмованої реакції. Таким чином, алостеричний інгібітор зменшує максимальну швидкість розгальмованої реакції за рахунок фактора$\left(1+I / K_{i}\right)$, який може бути великим, якщо концентрація алостеричного інгібітора є значною.