Skip to main content
LibreTexts - Ukrayinska

6.2: Кінетика ферментів

  1. Last updated
  2. Save as PDF
  • Page ID
    66712

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ферменти - це каталізатори, як правило, білки, які допомагають перетворити інші молекули, звані субстратами, в продукти, але самі по собі незмінні реакцією. Кожен фермент має високу специфічність хоча б для однієї реакції, і він може прискорити цю реакцію в мільйони разів. Без ферментів більшість біохімічних реакцій протікають занадто повільно, щоб життя було можливо. Ферменти настільки важливі для нашого життя, що мутація однієї амінокислоти в одному ферменті з більш ніж 2000 ферментів в нашому організмі може призвести до важкого або летального генетичного захворювання.

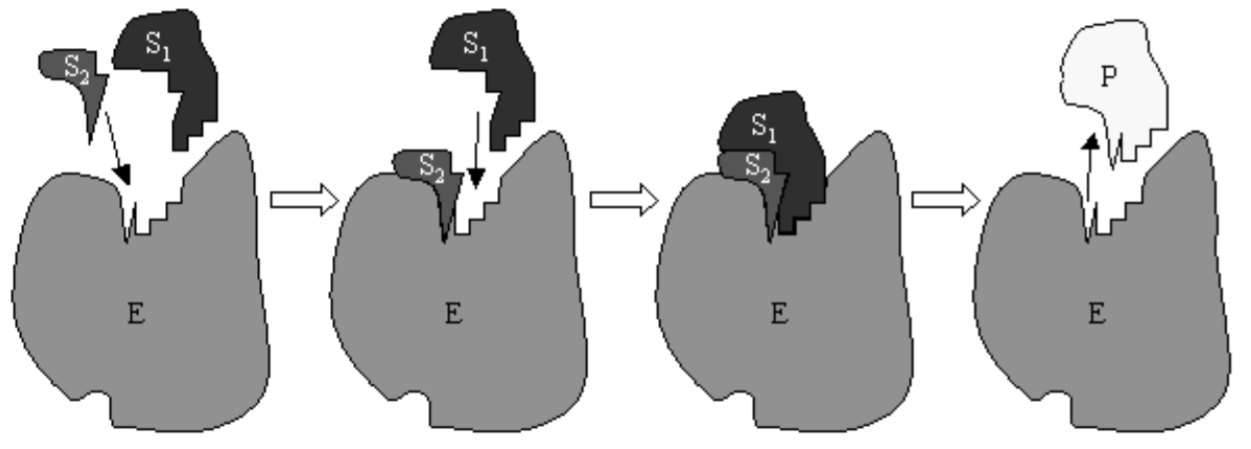
    clipboard_e61a227024967d5f7284106b1afcdf95a.png
    Малюнок 6.1: Реакція Міхаеліса-Ментена двох субстратів, що перетворюються в один продукт. (Намальовано User:ImeowBot, випущений за ліцензією GNU Free Documentation License.)

    де\(C\) - комплекс, утворений ферментом і субстратом. Мультфільм реакції Міхаеліса-Ментена з ферментом, що каталізує реакцію між двома субстратами, показаний на рис. 6.1. Зазвичай субстрат безперервно забезпечується реакцією і продукт безперервно видаляється. Видалення продукту було змодельовано, нехтуючи зворотною реакцією\(P+E \rightarrow C\). Безперервне забезпечення субстратом дозволяє припустити, що\(S\) утримується при приблизно постійній концентрації.

    Диференціальні рівняння для\(C\) і\(P\) можуть бути отримані за законом масової дії:

    \[\begin{aligned} &d C / d t=k_{1} S E-\left(k_{-1}+k_{2}\right) C \\[4pt] &d P / d t=k_{2} C . \end{aligned} \nonumber \]

    Біохіміки зазвичай хочуть визначити швидкість реакції з\(d P / d t\) точки зору концентрації субстрату\(S\) та загальної концентрації ферменту\(E_{0}\). Ми можемо виключити на\(E\) користь\(E_{0}\) закону збереження, що фермент, вільний і пов'язаний, зберігається; тобто

    \[\frac{d(E+C)}{d t}=0 \quad \Longrightarrow \quad E+C=E_{0} \quad \Longrightarrow \quad E=E_{0}-C \nonumber \]

    і ми можемо переписати рівняння для\(d C / d t\) усунення\(E\):

    \[\begin{align} \nonumber \frac{d C}{d t} &=k_{1} S\left(E_{0}-C\right)-\left(k_{-1}+k_{2}\right) C \\[4pt] &=k_{1} E_{0} S-\left(k_{-1}+k_{2}+k_{1} S\right) C \end{align} \nonumber \]

    Оскільки\(S\) передбачається постійним, комплекс, як очікується,\(C\) знаходиться в рівновазі, при цьому швидкість утворення дорівнює швидкості дисоціації. З цим так званим квазістаєвим наближенням, ми можемо припустити, що\(C=0\) в\((6.3.4)\), і ми маємо

    \[C=\frac{k_{1} E_{0} S}{k_{-1}+k_{2}+k_{1} S} \nonumber \]

    Швидкість реакції потім задається

    \[\begin{align} \nonumber \frac{d P}{d t} &=k_{2} C \\[4pt] \nonumber &=\frac{k_{1} k_{2} E_{0} S}{k_{-1}+k_{2}+k_{1} S} \\[4pt] &=\frac{V_{m} S}{K_{m}+S} \end{align} \nonumber \]

    де визначено дві основні константи:

    \[K_{m}=\left(k_{-1}+k_{2}\right) / k_{1}, \quad V_{m}=k_{2} E_{0} . \nonumber \]

    Константа Міхаеліса-Ментена або постійна Міхаеліса\(K_{m}\) має одиниці концентрації, а максимальна швидкість реакції\(V_{m}\) має одиниці концентрації, розділені на час. Тлумачення цих констант виходить при розгляді наступних меж:

    \[\begin{array}{ll} \text { as } S \rightarrow \infty, & C \rightarrow E_{0} \text { and } d P / d t \rightarrow V_{m} \\[4pt] \text { if } S=K_{m}, & C=\frac{1}{2} E_{0} \text { and } d P / d t=\frac{1}{2} V_{m} . \end{array} \nonumber \]

    Отже,\(V_{m}\) гранична швидкість реакції, отримана шляхом насичення реакції субстратом таким чином, що кожен фермент зв'язується; і\(K_{m}\) є концентрацією,\(S\) при якій тільки половина ферментів зв'язується, а реакція протікає на половині максимальна швидкість.