4.6: Еволюція вірулентності

Last updated
Save as PDF

Page ID: 66624

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Мікроорганізми постійно еволюціонують через тиск відбору в їх середовищах. Антибіотики є загальним джерелом селекційного тиску на патогенні бактерії, а розвиток стійких до антибіотиків штамів представляє серйозну проблему для здоров'я медичної науки. Бактерії та віруси також безпосередньо конкурують один з одним за репродуктивний успіх, що призводить до еволюції вірулентності. Тут, використовуючи модель ендемічної хвороби SIR, ми вивчаємо, як може розвиватися вірулентність.

Для аргументу ми припустимо, що популяція спочатку знаходиться в рівновазі з ендемічним захворюванням, викликаним вірусом дикого типу; тобто$S, I$ і$R$ приймаються ненульовими та рівноважними значеннями. Тепер припустимо, що деякі вірусні частинки мутують випадковим, неспрямованим процесом, який відбувається природним шляхом. Ми хочемо визначити умови, за яких мутантний вірус замінить вірус дикого типу в популяції. У математичному плані ми хочемо визначити лінійну стабільність рівноваги ендемічного захворювання до введення мутантного вірусного штаму.

Ми припускаємо, що оригінальний вірус дикого типу має рівень зараження$\beta$$\gamma$, швидкість видалення та смертність, пов'язану із захворюваннями$c$, і що мутантний вірус має відповідні показники,$\beta^{\prime}, \gamma^{\prime}$ і$c^{\prime} .$ ми також припускаємо, що індивід, заражений або диким, або мутантним вірусом, отримує імунітет до подальшого зараження як від дикого типу, так і від мутантних вірусних форм. Таким чином, наша модель має один сприйнятливий клас$S$, два різних інфекційних класи$I$ і$I^{\prime}$ залежно від того, який вірус викликає інфекцію, і один відновлений клас$R$. Відповідна схема

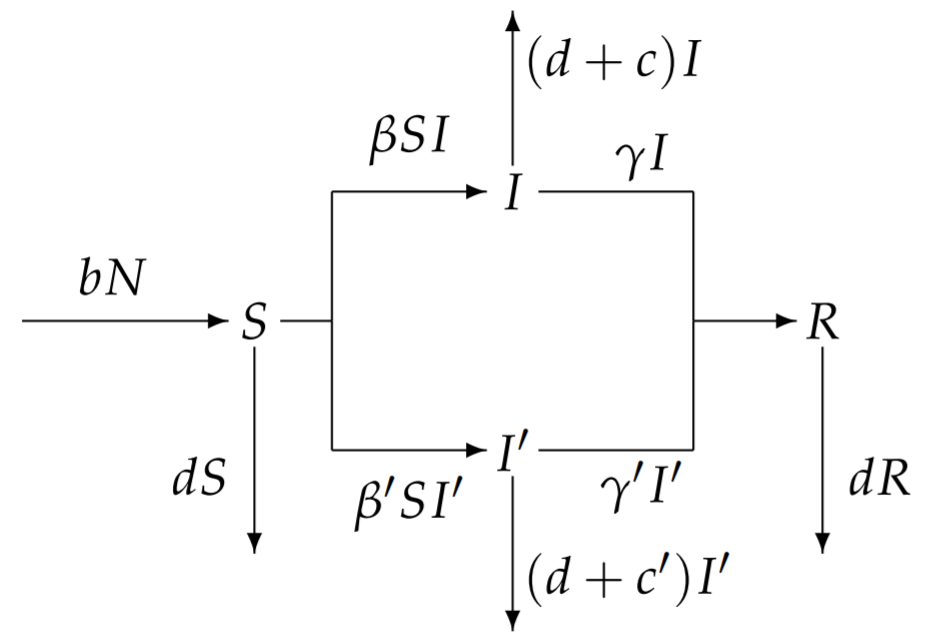
$clipboard_e1e1983ef71bdd1678a1c14b188424480.png$

з відповідними диференціальними рівнян

\[\begin{align} \frac{d S}{d t} &=b N-d S-S\left(\beta I+\beta^{\prime} I^{\prime}\right) \\[4pt] \frac{d I}{d t} &=\beta S I-(d+c+\gamma) I \\[4pt] \frac{d I^{\prime}}{d t} &=\beta^{\prime} S I^{\prime}-\left(d+c^{\prime}+\gamma^{\prime}\right) I^{\prime} \\[4pt] \frac{d R}{d t} &=\gamma I+\gamma^{\prime} I^{\prime}-d R \end{align} \nonumber \]

Якщо популяція спочатку знаходиться в рівновазі з вірусом дикого типу, то маємо$\dot{I}=0$ з$I \neq 0$, а значення рівноваги для$S$ визначається з (4.6.2) бути

\[S_{*}=\frac{d+c+\gamma}{\beta}, \nonumber \]

що відповідає основному репродуктивному співвідношенню$\beta S_{*} /(d+c+\gamma)$ єдності.

Ми порушуємо цю ендемічну рівновагу хвороби, вводячи невелику кількість інфекційних засобів, що несуть мутований вірус, тобто дозволяючи$I^{\prime}$ бути маленьким. Замість того, щоб розв'язувати задачу стійкості за допомогою якобійського аналізу, ми можемо безпосередньо вивчити рівняння для$d I^{\prime} / d t$ заданого (4.6.3). Тут, з$S=S_{*}$ заданим (4.6.5), ми маємо

\[\frac{d I^{\prime}}{d t}=\left[\frac{\beta^{\prime}(d+c+\gamma)}{\beta}-\left(d+c^{\prime}+\gamma^{\prime}\right)\right] I^{\prime} \nonumber \]

і$I^{\prime}$ збільшується в геометричній прогресії, якщо

\[\frac{\beta^{\prime}(d+c+\gamma)}{\beta}-\left(d+c^{\prime}+\gamma^{\prime}\right)>0 \nonumber \]

або після якоїсь елементарної алгебри,

\[\frac{\beta^{\prime}}{d+c^{\prime}+\gamma^{\prime}}>\frac{\beta}{d+c+\gamma} \nonumber \]

Наш результат (4.6.8) свідчить про те, що ендемічні віруси (або інші мікроорганізми), як правило, еволюціонуватимуть (i) легше передаватися між людьми$\left(\beta^{\prime}>\beta\right) ;$ (ii), щоб змусити людей хворіти довше$\left(\gamma^{\prime}<\gamma\right)$, і; (iii) бути менш смертельними$c^{\prime}<c$. Іншими словами, віруси еволюціонують, щоб збільшити свої основні репродуктивні співвідношення. Наприклад, наша модель передбачає, що віруси розвиваються менш смертельними, оскільки мертві не поширюють хвороби. Наш результат не був би застосовний, однак, якби померлі насправді поширювали хворобу, можливість, якщо позбавлення померлих не було зроблено з достатньою обережністю, можливо, через певні культурні традиції, такі як сімейне миття мертвого тіла.