7.9: Проблемний банк

Last updated

Oct 27, 2022
Save as PDF
- 7.8: Геометрія в мистецтві та науці
- 8: Подорож на Hōkūle'a

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Завдання 18

У розділі Tangrams ви вперше побачили всі 7 частин танграм, розташованих у квадрат.

Якщо великий квадрат, який ви зробили з усіма сімома частинами, є одним цілим, призначте (дробове) значення кожному з семи частин танграма. Обґрунтуйте свої відповіді.
Головоломка танграм містить невеликий квадрат. Якщо маленький квадрат (єдиний шматок танграма) є одним цілим, призначте значення кожному з семи частин танграма. Обґрунтуйте свої відповіді.
Набір танграм містить два великих трикутника. Якщо великий трикутник (єдиний шматок танграма) є одним цілим, призначте значення кожному з семи частин танграм. Обґрунтуйте свої відповіді.
Набір танграм містить один середній трикутник. Якщо середній трикутник (єдиний шматок танграма) є одним цілим, призначте значення кожному з семи частин танграма. Обґрунтуйте свої відповіді.
Набір танграм містить два маленьких трикутника. Якщо маленький трикутник (єдиний шматок танграма) є одним цілим, призначте значення кожному з семи частин танграма. Обґрунтуйте свої відповіді.

Завдання 19

По можливості намалюйте приклад наступних трикутників. Якщо це неможливо, поясніть, чому б і ні.

Прямокутний трикутник, який є сходами.
Прямокутний трикутник, який є рівнобедреним.
Прямокутний трикутник, який є рівностороннім.

Завдання 20

По можливості намалюйте приклад наступних трикутників. Якщо це неможливо, поясніть, чому б і ні.

Гострий трикутник, який є сходами.
Гострий трикутник, який є рівнобедреним.
Гострий трикутник, який є рівностороннім.

Завдання 21

По можливості намалюйте приклад наступних трикутників. Якщо це неможливо, поясніть, чому б і ні.

Тупого трикутника, який є сходами.
Тупого трикутника, який є рівнобедреним.
Тупого трикутника, який є рівностороннім.

Проблема 22

По можливості намалюйте приклад наступних трикутників. Якщо це неможливо, поясніть, чому б і ні.

Рівнокутний трикутник, який є сходами.
Рівнокутний трикутник, який є рівнобедреним.
Рівнокутний трикутник, який є рівностороннім.

Проблема 23

Подивіться на картинку нижче, на якій зображені дві лінії, що перетинаються. Кути A і D називаються «вертикальними кутами», а також кути B і C.

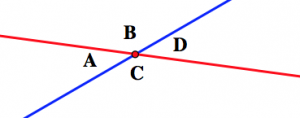
$vertical-300x118.png$

Використовуйте цей малюнок, щоб пояснити, чому вертикальні кути повинні мати однакову міру. (Підказка: яка сума мір кута A кута B? Звідки ти знаєш?)

Завдання 24

Дайте відповідь на наступні питання щодо трикутника нижче. Обов'язково орієнтуйтеся на те, що ви точно знаєте, а не на те, як виглядає картинка.

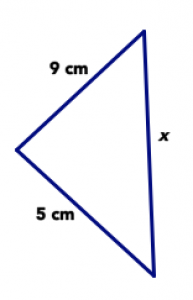
$triineq2-193x300.png$

Чи може бути правдою, що х = 4 см? Поясніть свою відповідь.
Чи може бути правдою, що х = 20 см? Поясніть свою відповідь.
Дайте три можливих значення x, виходячи з інформації на зображенні.

Завдання 25

Дайте відповідь на наступні питання щодо трикутника нижче. Обов'язково орієнтуйтеся на те, що ви точно знаєте, а не на те, як виглядає картинка.

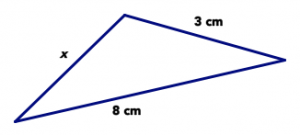
$triineq1-300x135.png$

Якщо х = 3 см, трикутник рівнобедрений. Чи можливо це? Поясніть свою відповідь.
Якщо х = 8 см, трикутник рівнобедрений. Чи можливо це? Поясніть свою відповідь.
Дайте три неможливі значення x, виходячи з інформації на зображенні.

Проблема 26

Професор Фабер намалював цю картину на дошці, сказавши, що вона показала три трикутники: △ ABC, △ ABD та △ CBD. Довжини сторін і вимірювання кута показані для кожного з трикутників.

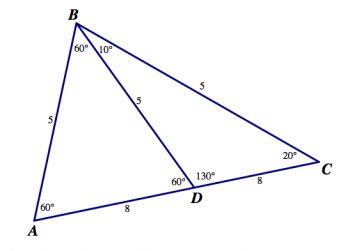
$badtris-350x251.png$

У цій картині багато помилок. Використовуйте те, що ви знаєте про довжину сторін і кути в трикутниках, щоб знайти всі помилки, які ви можете. За кожну помилку скажіть, що не так з картинкою, і чому це помилка. Поясніть своє мислення так чітко, як ви можете.

Завдання 27

Через конгруентність SSS трикутники надзвичайно міцні. Це означає, що вони часто використовуються в архітектурі та дизайні для забезпечення опор будівель, мостів та інших рукотворних об'єктів. Візьміть з собою камеру і знайдіть кілька місць у вашому районі або поблизу вашого кампусу, які використовують трикутні опори. Зробіть знімок і опишіть, що таке структура і де ви бачите трикутники.

Завдання 28

Можна створювати конструкції, які мають кілька симетрій. Подивіться, чи зможете ви знайти зображення (або створити свої власні!) які мають обидва:

симетрія відображення і обертальна симетрія,
відбиття симетрії і поступальної симетрії, і
обертальна симетрія і поступальна симетрія.