7.7: Симетрія

Last updated
Save as PDF

Page ID: 66262

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Математики використовують симетрію у всіляких ситуаціях. У розрахунках може бути симетрія, наприклад. Але найбільш впізнавані види симетрії - це геометричні конструкції.

Геометричні та реальні об'єкти можуть мати різні види симетрій ^[1].

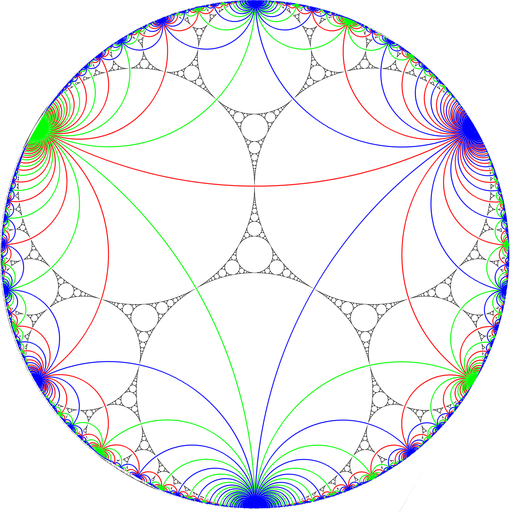
$512px-Mosaic_-_Mosquée_de_Paris.jpg$ $512px-Apolleangasket_symmetry.png$

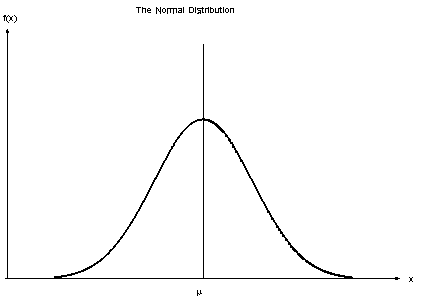
$512px-Swallowtail_Butterfly_Papilio_oribazus_8539896308.jpg$ $Starfish_02_paulshaffner_cropped.jpg$ $Normal_Distribution_NIST.gif$ $water-1759703_1920-300x160.jpg$

Або вони можуть взагалі не мати симетрії ^[2].

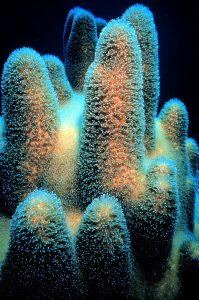
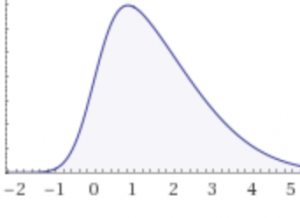
$PillarCoral-199x300.jpg$ $512px-Large_breaking_wave.jpg$ $picasso-250x300.jpg$ $skewnormal-300x218.png$ $serine.png$ $notsym-300x225.png$

Подумайте/Пара/Поділитися

Що ви вже знаєте про ідею симетрії? Що означає сказати, що дизайн симетричний?
Чи знаєте ви про різні типи симетрії? Які типи?
Чи можете ви навести приклади об'єктів реального світу, які є симетричними? А як щодо об'єктів, які не симетричні?

Симетрія ліній

Якщо ви можете перевернути фігуру над лінією - це називається відображенням фігури - а потім вона виглядає незмінною, тоді фігура має симетрію відображення або симетрію лінії. Лінія симетрії ділить об'єкт на дві дзеркально-зображувальні половини. Пунктирні лінії нижче - лінії симетрії:

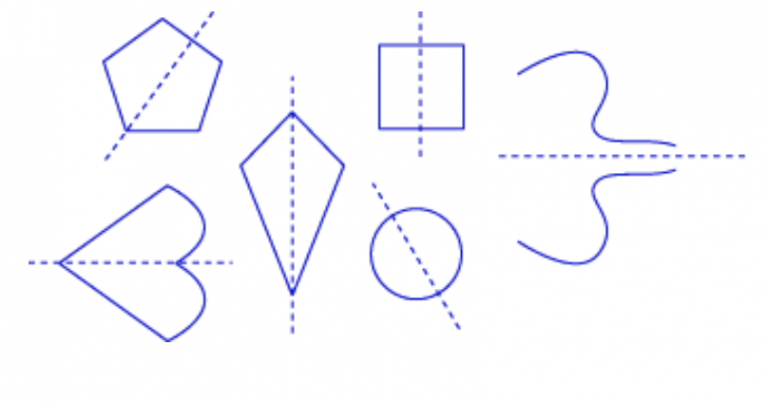
$linesym-768x403.png$

Порівняйте з пунктирними лініями нижче. Незважаючи на те, що вони розрізають фігури навпіл, вони не створюють дзеркальних половин. Це не лінії симетрії:

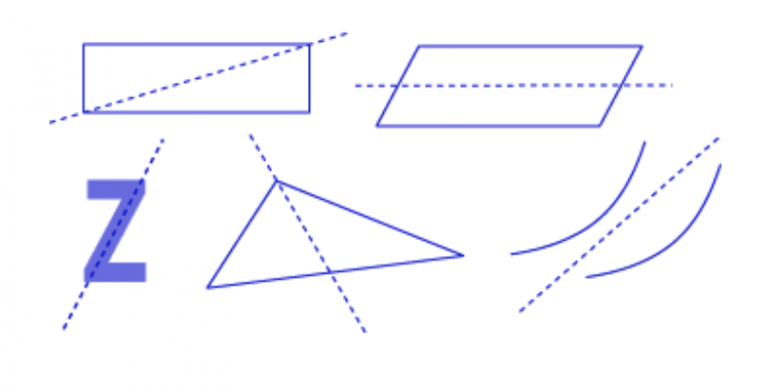
$notlinesym-768x392.png$

Подумайте/Пара/Поділитися

Подивіться на перший набір картинок на початку цієї глави. Чи є у кого-небудь з них лінії симетрії? Як ви можете сказати?

Проблема 12

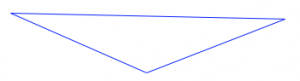
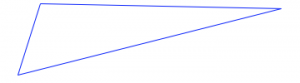
Для кожної з цифр ^[3] нижче:

Вирішіть, чи має він якісь лінії симетрії. Якщо ні, то звідки ви знаєте?
Якщо він має одну або кілька ліній симетрії, знайдіть/опишіть їх усі. Поясніть, як ви це зробили.

$trap1-300x100.png$ $smsq.png$

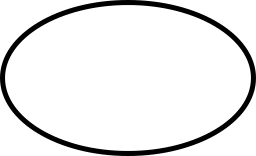
$256px еліпси_1.svg_.png$ $256px-диск_1.svg_.png$

$rect-300x84.png$

$scaltri-300x81.png$ $scatri-300x83.png$

Проблема 13

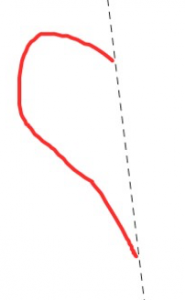
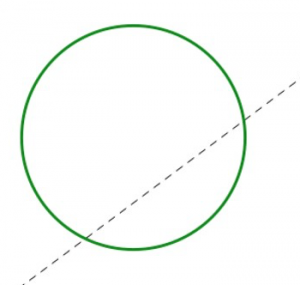
Кожна картинка нижче показує половину дизайну з лінійною симетрією. Показана лінія симетрії (пунктирна). Чи можете ви завершити дизайн? Поясніть, як ви це зробили.

$finishlinesym1-185x300.png$

$finishlinesym2-300x285.png$

Обертальна симетрія

Якщо ви можете повернути фігуру навколо центральної точки менше, ніж повне коло - це називається поворотом - і фігура виглядає незмінною, то фігура має обертальну симетрію. Точка, навколо якої ви обертаєте, називається центром повороту, а найменший кут, який потрібно повернути, називається кутом повороту.

Ця зірка має обертальну симетрію 72°, а центр обертання - центр зірки. Одна точка позначена, щоб допомогти вам візуалізувати обертання.

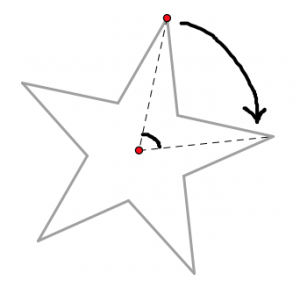
$starrot1-300x295.png$ $starrot2-300x300.png$

Подумайте/Пара/Поділитися

Як можна бути впевненим, що кут повороту зірки дорівнює рівно 72°?
Подивіться на перший набір картинок на початку цієї глави. Чи є у кого-небудь з них обертальна симетрія? Як ви можете сказати?

Проблема 14

Кожна з представлених нижче фігур має обертальну симетрію. Знайдіть центр повороту і кут повороту. Поясніть своє мислення.

$rotsym1.png$ $rotsym2-300x261.png$

Проблема 15

На кожному малюнку нижче показана частина конструкції з позначеним центром повороту та заданим кутом повороту. Чи можете ви завершити конструкцію так, щоб вона мала правильну обертальну симетрію? Поясніть, як ви це зробили.

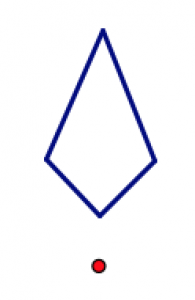
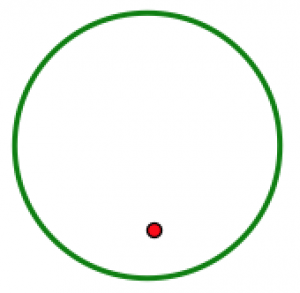
$makerot1-195x300.png$ $makerot2-300x293.png$

90° 45°

Поступальна симетрія

Переклад (його також називають слайдом) передбачає переміщення фігури в певному напрямку на певну відстань. Вектор (відрізок лінії зі стрілкою на одному кінці) може бути використаний для опису перекладу, оскільки вектор повідомляє як відстань (довжину відрізка), так і напрямок (напрямок, на який вказує стрілка).

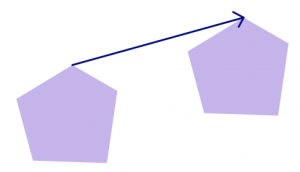
$vectrans-300x172.png$

Конструкція має поступальну симетрію, якщо на ній можна виконати переклад, і малюнок виглядає незмінним. Цегляна стіна ^[4] має поступальну симетрію у багатьох напрямках!

$512px-Solna_Brick_wall_Stretcher_bond_variation1.jpg$

Цегляна стіна - це один із прикладів тесселяції ^[5], про який ви дізнаєтеся більше в наступному розділі.

$tritesselate-225x244.png$ $512px-Uniform_tiling_333-t012.png$ $512px-Snub_square_rhombic_tiling_2.png$

Ви можете побачити симетрію перекладу у багатьох місцях. Це в архітектурі та дизайні ^[6].

$512px-Israel-2013-Jerusalem-Temple_Mount-Dome_of_the_Rock-Detail_01.jpg$ $mosque-300x225.jpg$ $256px-British_Museum_Great_Court_roof.jpg$

Це в мистецтві, найвідоміше, що M.C. Escher. (Можливо, ви захочете відвідати http://www.mcescher.com/gallery/symmetry/ і переглянути галерею «Симетрія».)

І це з'являється в традиційних гавайських та інших полінезійських ^{татуюваннях [7]}.

$256pX-ІЛС_Сендвіч_офіц_ду_рой_гранд_костюм_одессина_с_лерой_д.лерой_дапрес_JS. _Arago_grave_par_Lerouge_et_Forget.jpg$ $tattoo1-225x300.jpg$ $tattoo2-225x148.jpg$

Подумайте/Пара/Поділитися

На кожній з картинок з поступальною симетрією вище накидайте вектор для позначення напрямку і відстані поступальної симетрії.
Створіть власний дизайн з поступальною симетрією. Поясніть, як ви це зробили.

Мозаїчне зображення Марка Куперка (Flickr: Центральна мечеть Парижа) [CC BY 2.0], через Wikimedia Commons. Упаковка Аполлонського кола від Tomruen (Власна робота) [CC BY-SA 3.0], через Wikimedia Commons. Метелик Бернарда ДЮПОНА з ФРАНЦІЇ (Метелик ластівчин хвіст (Papilio oribazus)) [CC BY-SA 2.0], через Вікісховище. Морська зірка Пола Шафнера [CC BY 2.0], через Wikimedia Commons. Звичайне розповсюдження з Вікісховища [Публічне надбання]. Крапля води з pixababy.com [CC0 Creative Commons]. ←
Стовпні корали, хвилі та молекули з Вікісховища [Громадське надбання]. Голова жінки Пабло Пікассо, зображення з галереї Гендальфа на Flickr [CC-BY-NC-SA 2.0]
Коло та еліпс Парижа 16 (Власна робота) [CC BY-SA 4.0], через Вікісховище
Зображення Я, Xauxa [CC-BY-SA-3.0], через Вікісховище
Трикутна тесселяція від pixababy [CC0]. Гексагональні та ромбічні тесселяції з Вікісховища [Публічне надбання]. ←
Плитка в Єрусалимському храмі Андрія Шиви/Вікіпедія, через Вікісховище [CC BY-SA 4. 0]. Мечеть Хішама Бінсувайфа через flickr [CC BY-SA 2. 0]. Великий суд Британського музею Ендрю Данна, http://www.andrewdunnphoto.com/ (Власна робота) [CC BY-SA 2.0], через Wikimedia Commons
Королівський гавайський офіцер через Вікісховище [Публічне надбання]. Татуювання плечей та рук Мікаеля Faccio на мерехтінні [CC BY-2.0]. ←