7.4: Багатокутники

Last updated
Save as PDF

Page ID: 66274

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Може здатися, що вивчення геометрії в початковій школі - це не що інше, як вивчення купи визначень, а потім класифікація об'єктів. У цій частині ви вивчите деякі заходи щодо вирішення проблем та міркування, які базуються на геометрії. Але визначення все ж важливі! Отже, давайте почнемо з цього.

Визначення

Багатокутник - це:

плоска фігура
що обмежується кінцевою кількістю прямих відрізків
в якому кожен сегмент відповідає рівно двом іншим, по одному на кожній з його кінцевих точок.

Подумайте/Пара/Поділитися

Подібно до того, як першим кроком у вирішенні проблеми є розуміння проблеми, першим кроком у читанні математичного визначення є розуміння визначення.

Скористайтеся визначенням вище, щоб намалювати кілька прикладів фігур, які, безумовно, є багатокутниками. (Ви повинні бути в змозі сказати, чому ваш приклад відповідає визначенню.)
Намалюйте також кілька не-прикладів: фігури, які, безумовно, не є багатокутниками. (Ви повинні бути в змозі сказати, яка частина визначення не вдається для ваших не-прикладів.)

Кілька коментарів про багатокутники:

Відрізки лінії, що складають багатокутник, називаються його ребрами, а точки, де вони зустрічаються, називаються його вершинами (однина: вершина).
Через властивості (2) та (3) у визначенні межі багатокутників не є самоперетинаються.

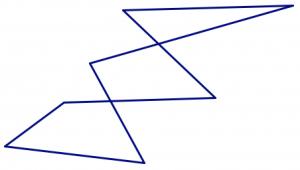
$notpoly-300x170.png$

Чи не багатокутник.

Багатокутники називаються на основі кількості сторін, які вони мають.

найменування	Кількість сторін	приклади
трикутник	3	$triex-1-300x83.png$
чотирикутний	4	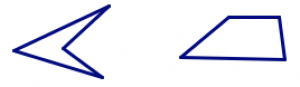$quadex-1-300x87.png$
п'ятикутник	5	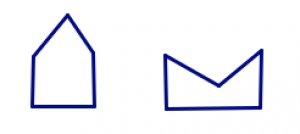$pentex-1-300x134.png$
шестикутник	6	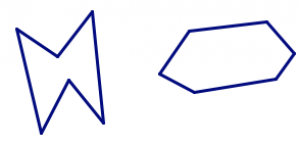$hexex-1-300x143.png$
гептагон	7
восьмикутник	8
нонагон	9
декагон	10

Загалом, ми називаємо багатокутник з n сторонами і n-кутником.

Проблема 6

На картинках нижче є багатокутники, приховані в дизайні. У кожній конструкції знайдіть всі трикутники, чотирикутники, п'ятикутники та шестикутники. Як ви можете бути впевнені, що знайшли їх усіх і не рахували двічі?

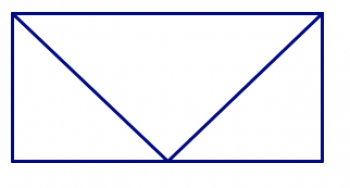
$design1-350x188.png$

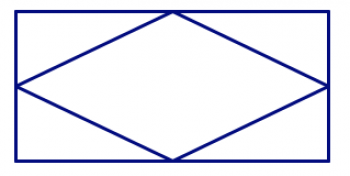
$design2-350x176.png$

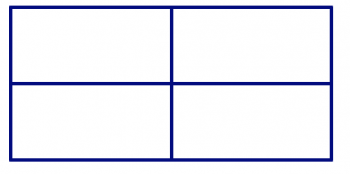
$design3-350x174.png$

$design4-350x177.png$

Сума кута

Ви знаєте, що сума внутрішніх кутів у будь-якому трикутнику становить 180°. Чи можете ви сказати що-небудь про кути в інших багатокутниках?

Ви, напевно, знаєте, що прямокутники мають чотири кути 90°. Отже, якщо всі чотирикутники мають однакову суму внутрішнього кута, вона повинна бути 360° (оскільки 4 × 90° = 360°).

Але зверніть увагу: у нас не обов'язково є підстави вважати, що ця постійна сума буде правдою. Пам'ятайте, що конгруентність SSS вірна для трикутників, але не для будь-яких інших багатокутників. Трикутники особливі, і ми не повинні припускати, що справжні твердження про трикутники будуть вірними для інших фігур.

Подумайте/Пара/Поділитися

Будь-чотирикутник можна розділити на два трикутника, де вершини трикутників збігаються з вершинами чотирикутника:

$splitquads-300x76.png$

Скористайтеся зображеннями вище, щоб уважно пояснити, чому всі чотирикутники дійсно мають суму кута 360°.

На свій розсуд

Працюйте над наступними вправами самостійно або з партнером.

Намалюйте на папері кілька різних п'ятикутників. Покажіть, що кожен з них можна розділити рівно на три трикутника таким чином, щоб вершини трикутників збігалися з вершинами п'ятикутника.
Використовуйте той факт, що кожен п'ятикутник можна розділити на три трикутника таким чином, щоб знайти суму кутів в будь-якому п'ятикутнику.
Намалюйте на папері кілька різних шестикутників. Покажіть, що кожен з них можна розділити рівно на чотири трикутника так, щоб вершини трикутників збігалися з вершинами шестикутника.
Використовуйте той факт, що кожен шестикутник можна розділити на чотири трикутника таким чином, щоб знайти суму кутів в будь-якому шестикутник.

Проблема 7

Використовуйте свою роботу над вправами вище, щоб завершити це загальне твердження:

Сума кута в багатокутників

Сума внутрішніх кутів у n-куті (багатокутник з n сторонами) дорівнює

__________________________.

Поясніть, як ви знаєте, що ваше твердження вірно.

Визначення

Правильний багатокутник має всі сторони однакової довжини, а всі кути однакову міру.

Наприклад, квадрати - це правильні чотирикутники - всі чотири сторони мають однакову довжину, а всі чотири кути вимірюють 90°. Але неквадратний прямокутник не є правильним. Незважаючи на те, що всі кути становлять 90°, сторони не всі однакові довжини. Аналогічно, неквадратний ромб не є правильним. Навіть незважаючи на те, що сторони ромба мають однакову довжину, кути можуть бути різними.

$regnotreg-1-768x166.png$

Проблема 8

Оскільки квадрат - це звичайний чотирикутник, ви знаєте, що кожен кут у звичайному чотирикутник вимірює 90°. А як щодо кутів в інших правильних багатокутників?

Яка міра кожного кута в правильному трикутнику? Поясніть, як ви знаєте, що маєте рацію.
Яка міра кожного кута в звичайному п'ятикутнику? Поясніть, як ви знаєте, що маєте рацію.
Яка міра кожного кута в правильному шестикутнику? Поясніть, як ви знаєте, що маєте рацію.
Яка міра кожного кута в правильному n-куті? Поясніть, як ви знаєте, що маєте рацію.