7.3: Трикутники та чотирикутники
- Page ID
- 66289
Дотримуйтесь цих вказівок самостійно:
- Намалюйте будь-який трикутник на папері.
- Намалюйте другий трикутник, який певним чином відрізняється від першого. Запишіть речення або два, щоб сказати, як воно відрізняється.
- Намалюйте третій трикутник, який відрізняється від обох ваших інших двох. Опишіть, чим він відрізняється.
- Намалюйте ще два трикутника, відмінних від усіх тих, що були раніше.
Порівняйте свої трикутники і описи з партнером. Щоб зробити «різні» трикутники, вам доведеться змінити якусь особливість трикутника. Складіть список функцій, які ви або ваш партнер змінили.
Трикутники класифікуються за різними властивостями. Сенс вивчення геометрії полягає не в тому, щоб вивчити багато словникового запасу, але корисно використовувати правильні терміни для об'єктів, щоб ми могли чітко спілкуватися. Ось короткий словник деяких типів трикутників.
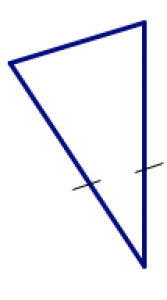
| розбіжності | рівнобедрений | рівносторонній |
|---|---|---|
 |
 |
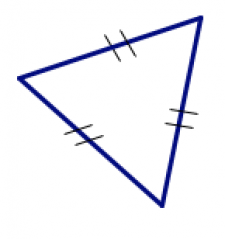 |
| всі сторони мають різну довжину | дві сторони мають однакову довжину | всі три сторони мають однакову довжину |
| гострий | тупий |
|---|---|
 |
 |
| всі внутрішні кути вимірюють менше 90° | один внутрішній кут вимірює більше 90 ° |
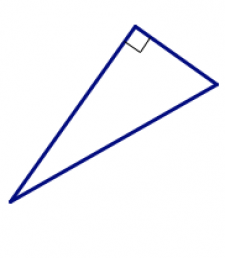
| правий | рівнокутні |
|---|---|
 |
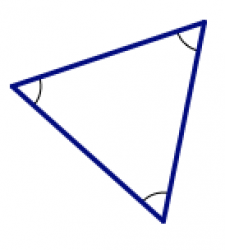 |
| один внутрішній кут вимірює рівно 90 ° | всі внутрішні кути мають однакову міру |
Пам'ятайте, що «геометрія - це мистецтво хороших міркувань від поганих малюнків». Це означає, що ви не завжди можете довіряти своїм очам. Якщо ви подивитеся на малюнок трикутника, і одна сторона виглядає так, ніби вона довша за іншу, це може означати, що малюнок був зроблений трохи неохайно.
Математики або записують вимірювання, або використовують галочки, щоб вказати, коли сторони і кути повинні бути рівні.
Якщо дві сторони мають однакове вимірювання або однакову кількість галочок, ви повинні вірити, що вони рівні і відповідно вирішити проблему, навіть якщо вона не виглядає так на ваші очі.
Ви можете побачити приклади цих на деяких зображеннях вище. Інший приклад - маленький квадрат, який використовується для позначення прямого кута на зображенні прямокутного трикутника.
На свій розсуд
Працюйте над наступними вправами самостійно або з партнером.
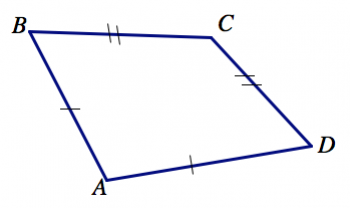
1. На малюнку нижче, які сторони мають однакову довжину (навіть якщо це не виглядає так на малюнку)?
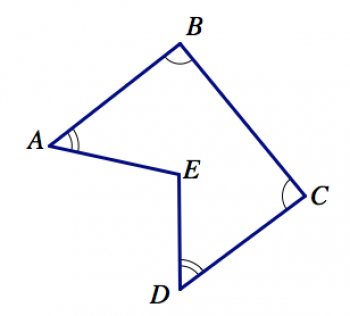
2. На малюнку нижче, які кути, як розуміють, мають однакову міру (навіть якщо це не виглядає так на кресленні)?
3. Ось сходовий трикутник. Намалюйте ще два рядових трикутника, кожен з яких певним чином відрізняється від показаного тут.

4. Ось гострий трикутник. Намалюйте ще два гострих трикутника, кожен з яких якимось чином відрізняється від показаного тут.

5. Ось тупий трикутник. Намалюйте ще два тупих трикутника, кожен з яких певним чином відрізняється від показаного тут.

6. Ось прямокутний трикутник. Намалюйте ще два правильних трикутника, кожен з яких певним чином відрізняється від показаного тут. Обов'язково вкажіть, який кут дорівнює 90°.

7. Ось рівнобедрений трикутник. Намалюйте ще два рівнобедрених трикутника, кожен з яких певним чином відрізняється від показаного тут. Використовуйте галочки, щоб вказати, які сторони рівні.

Кут Сума
На даний момент ви намалювали кілька різних трикутників на своєму папері. Виберіть один з ваших трикутників і дотримуйтесь наступних вказівок:
- За допомогою ножиць виріжте трикутник.
- Відірвіть (не обрізайте) кути, а три вершини розташуйте разом. У вас повинно бути щось, що виглядає трохи схоже на цю картинку:
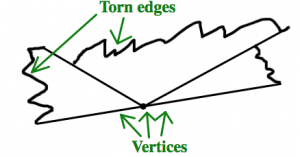
Що ви помічаєте? Що це говорить про кути в трикутнику?
Ви можете пам'ятати, дізнавшись, що сума кутів у будь-якому трикутнику становить 180°. У вашому класі тепер є багато прикладів трикутників, де сума кутів здається 180°. Але пам'ятайте, наші малюнки не точні. Як ми можемо бути впевнені, що наші очі нас не обманюють? Як ми можемо бути впевнені, що сума кутів у трикутнику не 181° або 178°, а насправді 180° на носі в кожному випадку?
Що б переконати вас поза всякими сумнівами, що сума кутів у будь-якому трикутнику становить 180°? Було б достатньо тестування багатьох випадків? Скільки вистачить? Чи могли б ви коли-небудь перевірити кожен можливий трикутник?
Історія: аксіоми Евкліда
Часто вчителі геометрії середньої школи доводять суму кутів у трикутнику 180°, зазвичай використовуючи деякі факти про паралельні лінії. Але (може, дивно?) так само добре сприймати це як аксіому, як даний факт про те, як працює геометрія, і йти звідти. Можливо, це менш задовольняє, ніж довести це з якоїсь іншої заяви, і якщо вам цікаво, ви можете, звичайно, знайти докази або ваш інструктор може поділитися з вами.
Приблизно в 300 році до н.е. Евклід [1] був першим математиком (наскільки ми знаємо), який намагався записати обережні аксіоми, а потім побудувати з цих аксіом суворі докази математичних істин.

Евклід
Евклід мав п'ять аксіом геометрії, перші чотири з яких здавалися математикам досить очевидними. Люди вважали, що це розумні припущення, з яких слід будувати геометричні істини:
- З огляду на дві точки, з'єднати їх можна прямим відрізком лінії.
- З огляду на відрізок лінії, ви можете продовжити його так далеко, як вам подобається, в будь-якому напрямку, зробивши лінію.
- Враховуючи відрізок лінії, ви можете намалювати коло, що має цей відрізок як радіус.
- Всі прямі кути є конгруентними.
П'ятий постулат турбував людей трохи більше. Спочатку це було викладено більш квітковою мовою, але це було еквівалентно цьому твердженню:
- Сума кутів у трикутнику дорівнює 180°.
Нескладно зрозуміти, чому ця п'ята аксіома викликала такий розбій в математиці. Це здавалося набагато менш очевидним, ніж інші чотири, і математики відчували, що вони якось обманюють, якщо вони просто припускали, що це, а не доводить, що це повинно бути правдою. Багато математиків витратили багато-багато років, намагаючись довести цю п'яту аксіому з інших аксіом, але вони не змогли цього зробити. І з поважною причиною: Є й інші види геометрії, де перші чотири аксіоми вірні, але п'ята - ні!
Наприклад, якщо ви робите геометрію на сфері - як баскетбол або, що важливіше, на поверхні Землі, - а не на плоскій площині, перші чотири аксіоми вірні. Але трикутники трохи дивні на поверхні землі. Кожен трикутник, який ви можете намалювати на поверхні землі, має суму кута строго більше 180°. Фактично, ви можете намалювати трикутник на Землі, який має три прямих кути [2], склавши суму кута 270°.
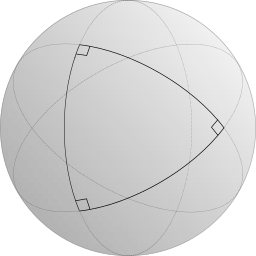
Трикутник з трьома прямими кутами на сфері.
На такій сфері, як Земля, сума кута не є постійною серед усіх трикутників. Великі трикутники мають більші суми кутів, а менші трикутники мають менші суми кутів, але навіть крихітні трикутники мають суми кутів, які перевищують 180°.
Геометрія, яку ви вивчаєте в школі, називається евклідовою геометрією; це геометрія плоскої площини, плоского світу. Це досить гарне наближення для маленького шматочка Землі, який ми бачимо в будь-який момент часу, але це не єдина геометрія там!
Нерівність трикутника
Зробіть копію з цих смужок паперу і виріжте їх. Вони мають довжину від 1 одиниці до 6 одиниць. Можливо, ви захочете розфарбувати смужки, написати на них цифри або зробити щось, що дозволяє легко відстежувати різну довжину.

Повторіть наступний процес кілька разів (принаймні 10) і відстежуйте результати (для вас запущена таблиця).
- Візьміть три смужки паперу. (Довжини не повинні відрізнятися один від одного; тому у вас є кілька копій кожної довжини.)
- Спробуйте зробити трикутник з цими трьома смужками, і вирішіть, чи вважаєте ви це можливим чи ні. (Не перекривайте смужки, виріжте їх або складайте. Довжина смуг повинна бути довжиною сторін трикутника.)
| Довжина 1 | Довжина 2 | Довжина 3 | Трикутник? |
|---|---|---|---|
| 4 | 3 | 2 | так |
| 4 | 2 | 1 | ні |
| 4 | 2 | 2 | ?? |
Ваша мета - придумати правило, яке описує, коли три довжини зроблять трикутник, а коли - ні. Запишіть правило своїми словами.
Порівняйте своє правило з іншими учнями. Тоді скористайтеся своїм правилом, щоб відповісти на наступні питання. Майте на увазі, мета полягає не в тому, щоб намагатися побудувати трикутник, а передбачити результат виходячи з вашого правила.
- Припустимо, вас попросили зробити трикутник зі сторонами 40 одиниць, 40 одиниць і 100 одиниць довжини. Як ви думаєте, ви могли б це зробити? Поясніть свою відповідь.
- Припустимо, вас попросили зробити трикутник зі сторонами 2,5 одиниці, 2,6 одиниць і 5 одиниць довжини. Як ви думаєте, ви могли б це зробити? Поясніть свою відповідь.
Ви напевно придумали якусь версію цього твердження:
Сума довжин двох сторін в трикутнику більше довжини третьої сторони.
Звичайно, ми знаємо, що в геометрії ми не повинні вірити своїм очам. Потрібно шукати пояснення. Чому ваша заява має сенс?
Пам'ятайте, що «геометрія - це мистецтво хороших міркувань від поганих малюнків». Наші матеріали були не дуже точними, тож як ми можемо бути впевнені, що це правило, яке ми придумали, є правильним?
Ну і в цьому випадку правило дійсно якраз те саме, що і приказка «найкоротша відстань між двома точками - пряма лінія». Насправді це саме те, що ми маємо на увазі під словами пряма лінія в геометрії.
Конгруентність SSS
Ми говоримо, що два трикутника (або будь-які два геометричні об'єкти) є конгруентними, якщо вони точно однакової форми і однакового розміру. Це означає, що якби ви могли підібрати один з них і перемістити його, щоб покласти на інший, вони точно перекриваються.
Повторіть наступний процес кілька разів і стежте за результатами.
- Підберіть три смужки паперу, які обов'язково сформують трикутник.
- Спробуйте зробити два різних (неконгруентних) трикутника з однаковими трьома смужками паперу. Запишіть, якщо ви змогли це зробити.
Повторіть наступний процес кілька разів і стежте за результатами.
- Візьміть чотири смужки паперу і сформуйте з ними чотирикутник. (Якщо ваші чотири смужки не утворюють чотирикутника, підберіть ще чотири смужки.)
- Спробуйте зробити два різних (неконгруентних) чотирикутника з однаковими чотирма смужками паперу. Запишіть, якщо ви змогли це зробити.
Що ви помічаєте з проблем 4 і 5? Чи можете ви зробити загальне твердження, щоб описати те, що відбувається? Чи можете ви пояснити, чому ваша заява має сенс?
Ви напевно придумали якусь версію цього твердження:
Якщо два трикутника мають однакову довжину сторін, то трикутники конгруентні.
Це, безумовно, не вірно для чотирикутників. Наприклад, якщо вибрати чотири смужки, які мають однакову довжину, можна зробити квадрат:

Але ви також можете стиснути цей квадрат у неквадратний ромб. (Спробуйте!)

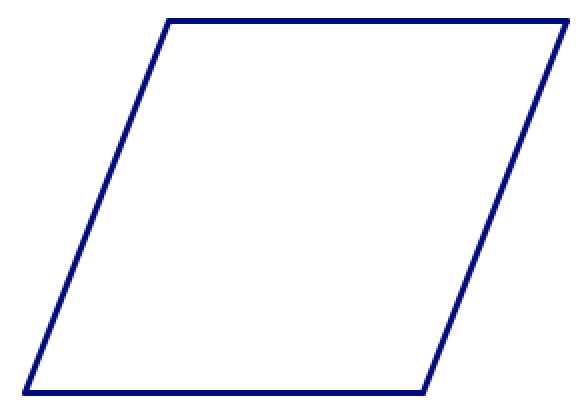
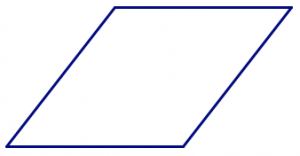
Якщо ви не виберете чотири довжини, які однакові, окрім «розтирання» форми, ви можете переставити сторони, щоб зробити різні (неконгруентні) форми. (Спробуйте!)
Ці два чотирикутника мають однакові чотири довжини сторін в тому ж порядку.
Ці два чотирикутника мають ті ж чотири довжини сторін, що і два вище, але сторони знаходяться в іншому порядку.
Але цього не може статися з трикутниками. Чому б і ні? Ну, звичайно, ви не можете переставити три сторони. Це було б так само, як обертати трикутник або перевертати його, але не робити нову форму.
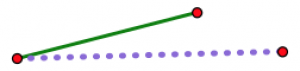
Чому трикутники не можуть «тиснути» так, як може чотирикутник (та інші форми)? Ось один із способів зрозуміти це. Уявіть, що ви вибираєте дві з трьох своїх довжин і покладіть їх один на одного, шарнірно в одному куті.

Це показує довший фіолетовий пунктирний сегмент і коротший зелений сегмент. Два сегменти шарнірно розташовані на червоній крапці зліва.
Тепер уявіть, що відкриваєте шарнір трохи за раз.

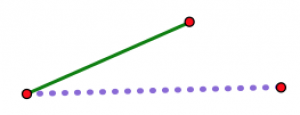
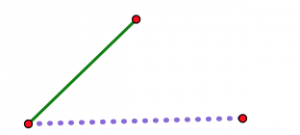
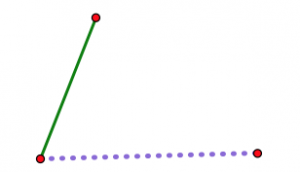

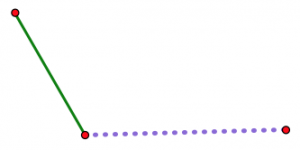
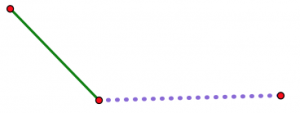
Коли шарнір відкривається, дві нешарнірні кінцеві точки стають все далі і далі один від одного. Незалежно від вашої третьої довжини (припускаючи, що ви насправді можете зробити трикутник з вашими трьома довжинами), є точно одне положення шарніра, де він буде точно відповідати, щоб закрити трикутник. Жодна інша посада не працюватиме.
- Портрет Евкліда з Вікісховища, ліцензований на умовах ліцензії Creative Commons Attribution 4.0 Міжнародна. ←
- Зображення Кояу/ Вікісховища, через Вікісховище, ліцензоване під Creative Commons Attribution-Share Alike 3.0 Неадаптована. ←