13.4: Кардинальність

Last updated
Save as PDF

Page ID: 66347

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Часто нас цікавить кількість елементів у множині або підмножині. Це називається кардинальністю набору.

Кардинальність

Кількість елементів у наборі - це кардинальність цього набору.

Кардинальність набору часто$A$ позначається як$|A|$ або$n(A)$

Приклад 12

Нехай$A=\{1,2,3,4,5,6\}$ і$B=\{2,4,6,8\}$

У чому полягає кардинальність$B ? A \cup B, A \cap B ?$

Рішення

Кардинальність$B$ полягає в$4,$ тому, що в наборі є 4 елементи.

Кардинальність$A \cup B$ є$7,$ з того$A \cup B=\{1,2,3,4,5,6,8\},$, що містить 7 елементів.

Кардинальність$A \cap B$ дорівнює 3, так як$A \cap B=\{2,4,6\}$, яка містить 3 елементи.

Приклад 13

У чому полягає$P=$ кардинальність безлічі англійських імен по місяцях року?

Рішення

Кардинальність цього набору полягає в$12,$ тому, що в році 12 місяців.

Іноді нас може зацікавити кардинальність об'єднання або перетину множин, але не знати фактичних елементів кожної множини. Це часто зустрічається в геодезичних зйомках.

Приклад 14

Опитування запитує 200 людей «Який напій ви п'єте вранці», і пропонує вибір:

Тільки чай
Тільки кава
І кава, і чай

Припустимо, 20 повідомляють тільки про чай, 80 повідомляють лише про каву, 40 повідомляють обидва. Скільки людей п'ють чай вранці? Скільки людей не п'ють ні чаю, ні кави?

Рішення

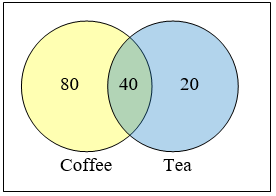$Два кола з написом «Кава і чай» перекриваються. Частина тільки в Coffee становить 80. Частина тільки в Чай становить 20. Частина, де вони перекриваються, дорівнює 40.$ На це питання найлегше відповісти, створивши діаграму Венна. Ми бачимо, що ми можемо знайти людей, які п'ють чай, додаючи тих, хто п'є лише чай, до тих, хто п'є обох: 60 людей.

Ми також можемо бачити, що ті, хто не п'є, не містяться ні в одній з трьох інших груп, тому ми можемо порахувати їх, віднімаючи від кардинальності універсального набору 200.

$200-20-80-40=60$люди, які не п'ють ні.

Приклад 15

Опитування запитує: Які онлайн-сервіси ви використовували за останній місяць:

Twitter
Facebook
Використовували обидва

Результати показують, що 40% опитаних використовували Twitter, 70% використовували Facebook, а 20% використовували обидва. Скільки людей не використовували ні Twitter, ні Facebook?

Рішення

Нехай$T$ буде набір всіх людей, які використовували Twitter, і$F$ бути набір всіх людей, які використовували Facebook. Зверніть увагу, що хоча кардинальність$F$ є$70 \%$ і кардинальність$T$ є$40 \%$, кардинальність не просто$70 \%+40 \%$, оскільки$F \cup T$ це буде вважати тих, хто користується обома послугами двічі. Щоб знайти кардинальність$F \cup T$, ми можемо додати кардинальність$F$ і кардинальність$T$, а потім відняти ті в перетині, які ми підрахували двічі. В символах,

$\mathrm{n}(F \cup T)=\mathrm{n}(F)+\mathrm{n}(T)-\mathrm{n}(F \cap T)$

$\mathrm{n}(F \cup T)=70 \%+40 \%-20 \%=90 \%$

Тепер, щоб знайти, скільки людей не користувалися жодною послугою, ми шукаємо кардинальність$(F \cup T)^{c}$. Оскільки універсальний набір містить$100 \%$ людей і кардинальність$F \cup T=90 \%$, кардинальність$(F \cup 7)^{c}$ повинна бути іншою$10 \%$

Попередній приклад ілюстрував дві важливі властивості:

властивості кардинальності

$\mathrm{n}(A \cup B)=\mathrm{n}(A)+\mathrm{n}(B)-\mathrm{n}(A \cap B)$

$n\left(A^{\circ}\right)=n(U)-n(A)$

Зверніть увагу, що перше властивість також можна записати в еквівалентній формі, вирішивши для кардинальності перетину:

$\mathrm{n}(A \cap B)=\mathrm{n}(A)+\mathrm{n}(B)-\mathrm{n}(A \cup B)$

Приклад 16

Додати текст тут.П'ятдесят студентів були опитані, і запитали, чи вони беруть соціальні науки (SS), гуманітарні (HM) або природничі науки (NS) курс наступного кварталу.

$\begin{array}{ll} \text{21 were taking a SS course} & \text{26 were taking a HM course} \\ \text{19 were taking a NS course} & \text{9 were taking SS and HM} \\ \text{7 were taking SS and NS} & \text{10 were taking HM and NS} \\ \text{3 were taking all three} & \text{7 were taking none} \end{array}$

Скільки студентів тільки проходять курс СС?

Рішення

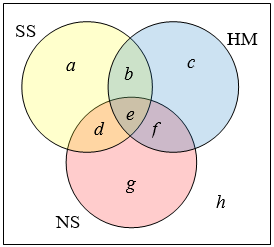$Діаграма Венна з трьох кіл, що перекриваються, позначені SS, HM та NS. Частина тільки в SS позначена а. Перекриття SS і HM позначено лише b. Частина тільки в HM позначена c. Перекриття SS і NS тільки позначено d. Перекриття всіх трьох позначено e. Перекриття HM і NS тільки позначено f. Частина в NS тільки позначена g. Частина, що знаходиться поза всіма трьома, позначається h.$ Це може допомогти подивитися на діаграму Венна.

З наведених даних ми знаємо, що в області 3 студенти$e$ та 7 студентів в області.$h$

оскільки 7 студентів проходили$N S$ курс, ми це знаємо$n(d)+n(e)=7$. оскільки ми знаємо, що в регіоні 3 є студенти 3, в регіоні повинні бути
$7-3=4$ студенти$S S$$d$

Аналогічно, оскільки є 10 студентів$\mathrm{NS}$, які беруть$\mathrm{HM}$ і, що включає регіони$e$ та$f$, повинні бути

$10-3=7$студенти області$f$

Оскільки 9 студентів приймали$\mathrm{SS}$ і$\mathrm{HM}$, в області повинні бути$9-3=6$ студенти$b$

Тепер ми знаємо, що 21 студент проходив курс СС. Сюди входять студенти з регіонів,$a, b, d,$ і$e .$ оскільки ми знаємо кількість студентів у всіх, крім регіону,$a,$ ми можемо визначити, що$21-6-4-3=8$ студенти знаходяться в регіоні.$a$

8 студентів проходять тільки курс SS.

Спробуйте зараз 4

Було опитано сто п'ятдесят людей і запитали, чи вірять вони в НЛО, привидів і снігових людей.

$\begin{array}{ll} \text{43 believed in UFOs} & \text{44 believed in ghosts} \\ \text{25 believed in Bigfoot} & \text{10 believed in UFOs and ghosts} \\ \text{8 believed in ghosts and Bigfoot} & \text{5 believed in UFOs and Bigfoot} \\ \text{2 believed in all three} & \text{} \end{array}$

Скільки опитаних людей вірили хоча б в одну з цих речей?

Відповідь: $Діаграма Венна з трьох колів, що перекриваються, позначені НЛО, Привиди та Снігова людина. Частина тільки в НЛО становить 30. Перекриття НЛО і привидів тільки 8. Частина в примарах лише 28. Перекриття НЛО і снігової людини тільки 3. Перекриття всіх трьох дорівнює 2. Перекриття привидів і снігової людини тільки 6. Частина у бігфута лише 14. Частина за межами всіх трьох - 59.$ Починаючи з перетину всіх трьох кіл, ми відпрацьовуємо свій вихід. Так як 10 людей вірять в НЛО і привидів, а 2 вірять у всі три, що залишає 8, які вірять тільки в НЛО і привидів. Ми відпрацьовуємо свій вихід, заповнюючи всі регіони. Після того, як ми це зробимо, ми можемо скласти всі ці регіони, отримавши 91 людина в об'єднанні всіх трьох наборів. Це залишає$150-91=59$ тих, хто не вірить ні в кого.