13.3: Діаграми Венна

Last updated
Save as PDF

Page ID: 66361

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Щоб візуалізувати взаємодію множин, Джон Венн в 1880 році думав використовувати перекриваються кола, відштовхуючись від подібної ідеї, яку використовував Леонхард Ейлер в 18 ^{столітті}. Ці ілюстрації тепер називаються діаграмами Венна.

Діаграма Венна

Діаграма Венна представляє кожну множину колом, зазвичай намальованим всередині коробки, що містить, що представляє універсальний набір. Області перекриття вказують на елементи, спільні для обох множин.

Основні діаграми Венна можуть ілюструвати взаємодію двох або трьох множин.

Приклад 9

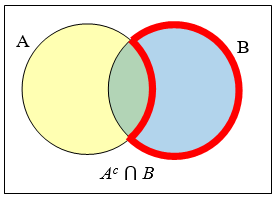
Створіть діаграми Венна для ілюстрації$A \cup B, A \cap B,$ та$A^{c} \cap B$

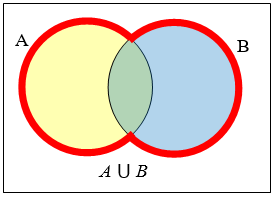$Діаграма Венна, яка показує два набори, що перекриваються A та B. Підсвічується область, що входить до складу будь-якого набору.$ $A \cup B$містить всі елементи в будь-якому наборі.

$A \cup B$містить всі елементи в будь-якому наборі.

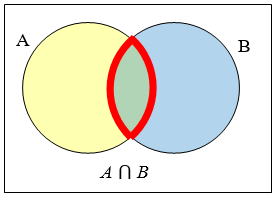
$Діаграма Венна, що показує два набори, що перекриваються A і B. Область перекриття, включена в обидва набори, підсвічується.$

$Діаграма Венна, яка показує два набори, що перекриваються A та B. Підсвічується область, яка включена лише в B, але не A.$ $A \cap B$містить тільки ті елементи в обох наборах - в перекритті кіл.

приклад 10

Використовуйте діаграму Венна для ілюстрації$(H \cap P)^{c} \cap W$

Почнемо з визначення всього в наборі$\mathrm{H} \cap P$

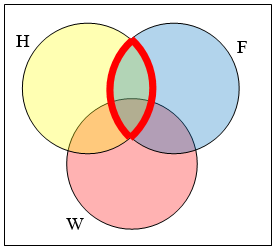
$Діаграма Венна з трьох множин H F і W показано перекриття. Підсвічується область, де H і F перекриваються.$

Тепер$(H \cap P)^{c} \cap W$ буде містити все, що не в наборі, визначеному вище, який також знаходиться в наборі$W$

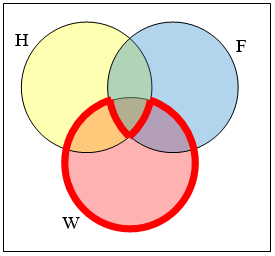
$Діаграма Венна з трьох множин H F і W показано перекриття. Область в наборі W виділяється, за винятком тієї частини, яка також лежить як в F, так і в H. Іншими словами, всі W, крім тієї частини, де всі три перекриваються.$

Приклад 11

Створіть вираз для представлення окресленої частини показаної діаграми Венна.

$Діаграма Венна з трьох множин H F і W показано перекриття. Область, де H і F перекриваються, а W - ні, виділяється.$ Елементи в окресленому$\mathrm{H}$ наборі знаходяться в множині і$F$, але не в множині$W$. Таким чином, ми могли б представити цей набір як$H \cap F \cap W$

Спробуйте зараз 3

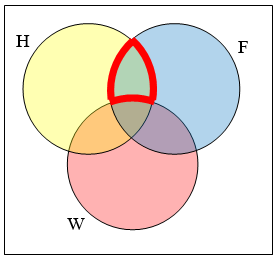
Створіть вираз для представлення окресленої частини показаної діаграми Венна

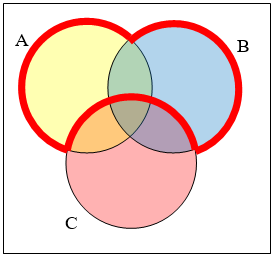
$Діаграма Венна з трьох множин A B і C показано перекриття. Виділена область включає в себе що-небудь в A або що-небудь в B, виключаючи що-небудь також в C$

Відповідь: $A \cup B \cap C^{c}$