12.3: Безстрокові
- Page ID
- 66691
Деякі стипендії, пропоновані студентам у вашому коледжі були створені десятиліття тому, але ці стипендії продовжують виплачувати гроші студентам щороку. Звідки беруться всі гроші? Хтось дарував надзвичайно великий фонд пожертвування всіх тих багато років тому, щоб підтримувати стипендію протягом десятиліть? Або фізична особа або допоміжна організація просто виплачує його з кишені щороку? Як це можливо, щоб ці стипендії виплачувалися через всі минулі роки і всі осяжні роки?
Що б ви зробили, якби виграли великий приз лотереї, такий як Lotto 6/49 або Lotto Max? Сьогоднішні заголовки постійно демонструють переможців лотереї, які виграють «великий», ставши за ніч мільйонерами. Зі своїми новоствореними доходами вони поспішають купувати будинки на мільйон доларів та розкішні транспортні засоби та віддавати задоволення життя. Колись незабаром після цього розповідаються історії про те, як ці мільйонери подають на банкрутство. Що робити, якби хтось сказав цим людям, що замість того, щоб витрачати гроші відразу, вони могли б інвестувати їх і використовувати відсотки, щоб жити назавжди; цілі покоління їхньої родини могли б отримати вигоду від виграшу. Тільки уявіть: якщо ви інвестуєте 5 мільйонів доларів під 5% відсотків, ви будете заробляти 250 000 доларів відсотків щороку, які ви могли б зняти нескінченно.
Ці сценарії підкреслюють важливість безстрокових коштів, які є ануїтетами, які мають нескінченний термін. На вашому індивідуальному рівні будь-яка сума грошей, яку ви інвестуєте як безстрокову, може бути використана для отримання доходу назавжди. На професійному рівні багато компаній та некомерційних організацій, таких як спортивні клуби, встановлюють стипендіальні програми та стипендії для своїх співробітників, членів або клієнтів. У деяких контрактах платежі, такі як роялті, тривають назавжди. Деякі розділені акції мають свою ціну, яка визначається невизначеною майбутньою сумою дивідендів.
У цьому розділі досліджується поняття безстроків. Ви розрахуєте інвестиції, необхідні для підтримки безстрокового терміну разом із сумою платежу.
Що таке безстрокові?
Безстроковий - це особливий тип ануїтету, який має фіксований, регулярні платежі тривають нескінченно довго. Якщо основна частина інвестицій ніколи не знімається, то відсотки, зароблені в кожному періоді, можуть бути зняті, не впливаючи на майбутній відсоток прибутку від інвестицій. Тому ануїтет продовжує заробляти однакову суму відсотків кожен майбутній інтервал і може виплачувати відсотки назавжди. Як єдиний депозит основної суми може витримати нескінченну суму платежів? Математично гроші, що відбуваються в далекому майбутньому, стають нікчемними, коли повертаються до сьогоднішнього дня, де вони не мають ніякої цінності.
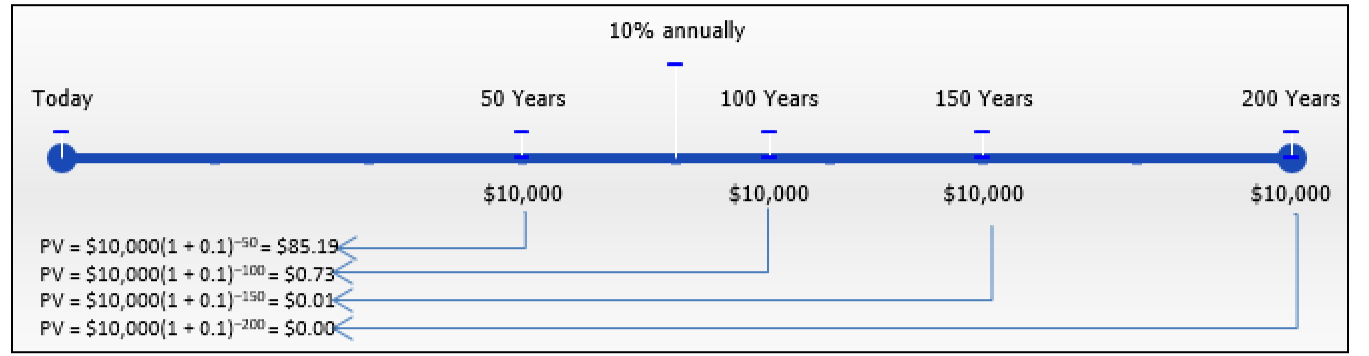
Щоб проілюструвати те, що гроші сьогодні нікчемні, цифра тут обчислює деякі теперішні значення платежів у розмірі 10 000 доларів, які відбуваються далеко в майбутньому. За допомогою різних розрахунків зверніть увагу, що коли платежі відбуваються далі в майбутньому, нинішня вартість практично не зменшується. Насправді, приблизно через 160 років 10 000 доларів сьогодні стає вартістю майже 0 доларів. Будь-які платежі, здійснені після цього моменту часу, призводять до таких незначних доповнень до теперішньої вартості, що по суті вони дійсно не мають подальшого впливу. Відповідно до цієї передумови, тоді можна визначити значення сьогодні, яке еквівалентно нескінченному майбутньому потоку ануїтетних платежів.
Звичайні безстрокові та безстрокові зобов'язання
Безстроковий - це особливий вид ануїтету. Він поставляється як у звичайних, так і в ануїтетних видах. Крім того, частота платежів та частота складання створюють або просту, або загальну ануїтетну структуру. Безстрокові можуть відбуватися навіть після періоду відстрочки, а отже, можливі відкладені безстроки.
Тут з'являється типова хронологія для вічності. Він ідентичний будь-якій іншій часовій шкалі ренти, за винятком двох відмінних характеристик:

- Майбутній часовий період. Замість того, щоб конкретний проміжок часу вказувався праворуч від часових ліній, з'являється слово «Назавжди», що представляє нескінченну природу вічності.
- Еквівалентність\(FV\) і\(PV\). Майбутня вартість безстрокового терміну така ж, як і поточна вартість, оскільки тільки відсотки коли-небудь виплачуються, а основна сума ніколи не торкається.
Формула
Як і формули ануїтету, формули безстрокового строку призначені для розміщення як простих, так і загальних ануїтетів через\(\dfrac{CY}{PY}\) показник, що гарантує, що інтервал складання відповідає інтервалу виплат. Ці нові формули представляють спрощені версії формул 11.4 та 11.5. Для ілюстрації нагадаємо Формулу 11.4:
\[PV_{ORD}=PMT\left[\dfrac{1-\left[\dfrac{1}{(1+i)^{\frac{CY}{PY}}}\right]^{N}}{(1+i)^{\frac{CY}{PY}-1}}\right] \nonumber \]
Дивлячись на чисельник, оскільки\(N\) він стає все більшим,\(\left[\dfrac{1}{(1+i)^{\frac{CY}{PY}}}\right]^{N}\) наближається до значення нуля, що ефективно видаляє його з рівняння. Це залишає чисельник 1 над знаменником.

Як це працює
Кроки, необхідні для вирішення поточної вартості безстрокового зобов'язання, залишаються по суті незмінними від вирішення для поточної вартості будь-якого ануїтету. Ці кроки, введені в Розділі 11.3, переглядаються для випадку безстроків:
Крок 1: Визначте тип безстрокового строку. Намалюйте часову шкалу, щоб візуалізувати питання.
Крок 2: Визначте змінні, які можуть бути відомі, включаючи\(IY, CY, PMT, PY\), і або\(PV_{ORD}\) або\(PV_{DUE}\). Якщо\(PV_{DUE}\) відомо\(PV_{ORD}\) або, то встановіть\(FV\) таку ж суму. Якщо ніякої теперішньої вартості не відомо, то\(FV\) встановіть 0 доларів, так як гроші в далекому майбутньому нічого не варті. На відміну від звичайних ануїтетів, вам не потрібно визначати Роки через відсутність N у всіх безстрокових розрахунках.
Крок 3: Використовуйте формулу 9.1 для розрахунку\(i\).
Крок 4: Ви ніколи не вимагаєте цього кроку, оскільки\(FV\) знаходиться так далеко в майбутньому, що ви можете автоматично переконатися, що його теперішнє значення дорівнює нулю.
Крок 5: Щоб обчислити теперішню величину, застосуйте або Формулу 12.5, або Формулу 12.6, залежно від типу безстрокового строку.
Як і у випадку з регулярними ануїтетами, якщо ви маєте справу з відкладеним безстроковим, то ви повинні змінити ці процедури, як ви б розрахувати відстрочені ануїтети (див. Розділ 12.1). Більшість безстрокових додатків вимагають обчислити або необхідні інвестиції (\(PV_{ORD}\)або\(PV_{DUE}\)), або платіж (\(PMT\)). Використовуйте алгебраїчну підстановку та перестановку, коли потрібні інші змінні.
Важливі примітки
Калькулятор BAII Plus налаштований лише для фіксованих строкових ануїтетів. Тому він не має певної вбудованої функції або способу введення безстрокового терміну. Однак, оскільки безстроковий термін є спеціалізованою версією звичайної ануїтету, кілька незначних адаптацій до ануїтетних входів дозволяють розрахувати безстрокові. Введіть всі змінні, як зазвичай, за винятком змін, показаних у таблиці нижче.
| Змінна | Рішення для\(PV_{ORD}\) або\(PV_{DUE}\) | Рішення для PMT |
|---|---|---|
| ФВ | \ (PV_ {ORD}\) або\(PV_{DUE}\) «>Призначити FV = 0, оскільки гроші в далекому майбутньому сьогодні нічого не варті. | Призначте FV рівне або PVORD або PVDUE, залежно від того, що відомо. Нагадаємо, що принципала ніколи не чіпають. |
| П | \ (PV_ {ORD}\) або\(PV_{DUE}\) «>Використовуйте велике значення, наприклад 10 000. * | Використовуйте велике значення, наприклад 2500. * |
* Це помістить FV далеко в далекому майбутньому. Більша величина може бути використана, але робити це потрібно з обережністю. Залежно від величин, що з'являються в безстроковому розрахунку, потужність, що виникає в результаті показника дуже великого N, може перевищувати обчислювальні можливості технології і видавати помилку. Якщо у вас виникла помилка, спробуйте трохи знизити значення.\(N\)
Шляхи до успіху
Формули 12.5 і 12.6 представляють спрощені версії формул 11.4 і 11.5. Якщо ви виявите ці нові формули заплутаними, або якщо ви просто хочете запам'ятати єдину формулу для теперішніх значень, ви можете вирішити будь-яке питання про вічне за допомогою формул глави 11. Якщо ви використовуєте ці формули, ви повинні підставити надзвичайно велике значення N в формулу, використовуючи технологію замін, розглянуту в таблиці вище.
- Якщо єдиний платіж поміщений сьогодні в звичайний безстроковий термін, чи буде його майбутня вартість вищою, нижчою чи однаковою?
- Якщо одноразова сума буде поміщена сьогодні на безстроковий термін, чи буде її майбутня вартість вищою, нижчою чи однаковою?
- Відповідь
-
- Це те саме після кожного зняття відсотків і вище між зняттям коштів.
- Це те саме безпосередньо перед будь-яким зняттям відсотків і завжди нижче між зняттям коштів. Нагадаємо, що перший платіж знімається негайно, в результаті чого основна сума залишається меншою, ніж початкова сума.
Кендра є директором з людських ресурсів і хоче запропонувати новий співробітник пільги через корпоративну стипендіальну програму. Щорічно 10 $1,000 стипендії повинні бути доступні дітям співробітників компанії. Якщо перші стипендії будуть пропонуватися щорічно, починаючи з одного року, яку суму потрібно інвестувати сьогодні в 7,5%, що збільшується щорічно, щоб безстроково фінансувати стипендіальну програму?
Рішення
Крок 1:
Розрахуйте суму сьогодні, яку необхідно інвестувати таким чином, щоб вона могла безстроково виплачувати необхідні кошти в кінці кожного року. Інтервали оплати і складання однакові, тому це звичайна проста безстрокова. Визначте теперішню вартість (\(PV_{ORD}\)).
Що ви вже знаєте
Крок 1 (продовження):
Хронологія для вічності відображається нижче.

Крок 2:
\(IY\)= 7,5%,\(CY\) = 1,\(PMT\) = 10 × 1000$ = 10 000$,\(PY\) = 1
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Не потрібен для безстроків.
Крок 5:
Застосовуємо формулу 12.5.
Виконувати
Крок 3:
\(i=7.5 \% / 1=7.5 \%\)
\[PV_{ORD}=\dfrac{\$ 10,000}{(1+0.075)^{\frac{1}{1}}-1}=\$ 133,333.33 \nonumber \]
Інструкції з калькулятора
| Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| КІНЕЦЬ | 10000 | 7.5 | Відповідь: -133,333.333 | 10000 | 0 | 1 | 1 |
Якщо Кендра має її компанію розмістити $133 333.33 на безстроковий рахунок, вона буде заробляти $10,000 відсотків під 7,5%, що щороку буде фінансувати стипендіальну програму безстроково.
На згадку про свого покійного батька, який був дуже успішним менеджером з маркетингу, Брайан хотів би створити маркетингову стипендіальну програму зі школою бізнесу свого університету. Він здатний пожертвувати $100,000 з маєтку свого батька, щоб створити фонд. Якщо безстроковий фонд може заробляти 6,3% в сукупності півроку, і перша стипендія повинна бути надана негайно, яку щорічну суму стипендії може запропонувати фонд?
Рішення
Крок 1:
Розрахуйте суму безстрокового платежу, яку може витримати внесок. Платежі та інтервали складання різні, тоді як платежі починаються негайно. Тому це загальне безстрокове зобов'язання. Визначте суму безстрокового платежу (ПМТ).
Що ви вже знаєте
Крок 1 (продовження):
Графік отримання стипендії відображається нижче.

Крок 2:
\(IY\)= 6,3%,\(CY\) = 2,\(PV_{DUE}\) = 100 000$,\(PY\) = 1
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Не потрібні в безстроках.
Крок 5:
Підставляємо в Формулу 12.6, переставляючи для\(PMT\).
Виконувати
Крок 3:
\(i=6.3 \% / 2=3.15 \% \)
Крок 5:
\[\$ 100,000=PMT\left(\dfrac{1}{(1+0.0315)^{\frac{2}{1}}-1}+1\right) \nonumber \]
\[\$ 100,000=PMT(16.626892) \nonumber \]
\[\$ 6,014.35=PMT \nonumber \]
Інструкції з калькулятора
| Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| ЛВ | 2500 | 6.3 | -100000 | Відповідь: 6,014.353018 | 100000 | 1 | 2 |
Пожертвування Брайана дозволить отримати негайну суму стипендії в розмірі 6 014,35 доларів США, яка залишить $100,000 − $6,014,35 = $93,985.65 основної суми на рахунку. Ця основна сума зможе заробити $6,014.35 безстроково щороку.
Одним із методів оцінки простих акцій є визначення поточної вартості її майбутніх дивідендів. Якщо IBM Corporation, за прогнозами, матиме дивіденди на кінець року в розмірі $1,50 на акцію протягом наступних трьох років, а потім $1,80 за акцію безстроково, скільки інвестор повинен бути готовий заплатити, якщо йому потрібна 12% збільшена квартальна норма прибутку?
Рішення
Крок 1:
Існують різні складання і платежі, а платежі здійснюються в кінці інтервалу. Тому це поєднання звичайної загальної ануїтету за перші три роки з подальшим звичайним загальним безстроком. Обчисліть поточну вартість простих акцій (\(PV_{ORD}\)).
Що ви вже знаєте
Крок 1 (продовження):
Нижче наведено часову шкалу звичайних акцій.
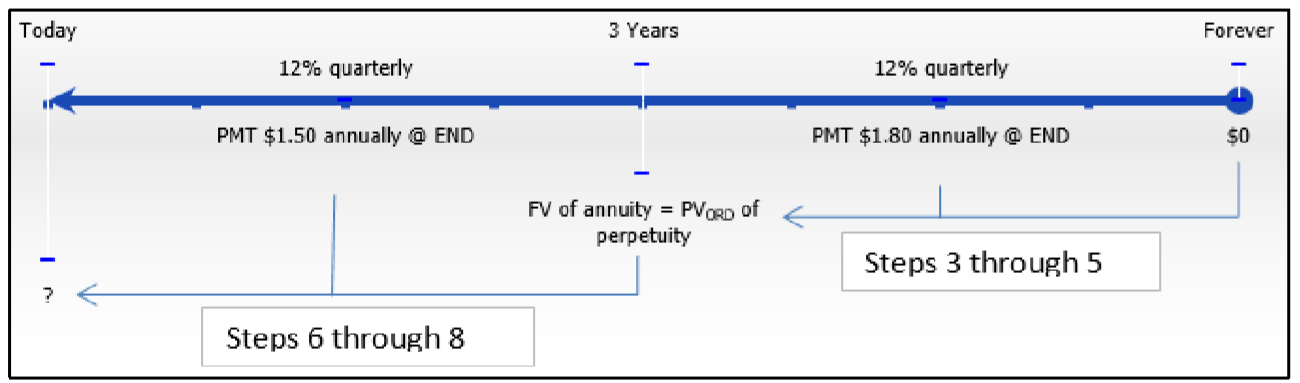
Крок 2:
Звичайна загальна безстрокова:\(IY\) = 12%,\(CY\) = 4,\(PMT\) = 1,80\(PY\) долара, = 1
Як ви туди потрапите
Починаючи з правого боку часової шкали, спочатку обчисліть теперішню вартість безстроку.
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Не потрібні в безстроках.
Крок 5:
Застосовуємо формулу 12.5. Потім розрахуйте теперішню вартість трирічної ануїтету.
Крок 6:
Застосуйте формули 9.2 та 9.5 (перестановка для\(PV\)), щоб знайти майбутню вартість\(PV_{ORD}\) єдиного платежу (який є безстроковим).
Крок 7:
Застосовуйте Формулу 11.1 і Формулу 11.4 до ануїтету.
Крок 8:
Додайте результати кроку 6 та кроку 7, щоб отримати вартість акцій сьогодні.
Виконувати
Крок 3:
\(i=12 \% / 4=3 \%\)
Крок 5:
\[PV_{ORD}=\dfrac{\$ 1.80}{(1+0.03)^{\frac{4}{1}}-1}=\$ 14.341622 \nonumber \]
Крок 6:
\(N=4 \times 3=12 \text { compounds } \)
\[\$ 14.341622=PV(1+0.03)^{12} \nonumber \]
\[PV=\$ 14.341622 \div(1+0.03)^{12}=\$ 10.058925 \nonumber \]
Крок 7:
\(N=1 \times 3=3 \text { payments }\)
\[PV_{ORD }=\$ 1.50\left[\dfrac{1-\left[\frac{1}{(1+0.03)^{\frac{4}{1}}}\right]^{3}}{(1+0.03)^{\frac{4}{1}}-1}\right]=\$ 3.568914 \nonumber \]
Крок 8:
\[\$ 10.058925+\$ 3.568914=\$ 13.63 \nonumber \]
Інструкції з калькулятора
| Сходинки | Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|---|
| 3 - 5 | КІНЕЦЬ | 10000 | 12 | Відповідь: -14.341622 | 1.8 | 0 | 1 | 4 |
| 6 - 8 | \(\surd\) | 3 | \(\surd\) | Відповідь: -13.627839 | 1.5 | 14.34 1622 | \(\surd\) | \(\surd\) |
Якщо інвестор бажає 12% рентабельності своїх інвестицій, він був би готовий заплатити $13,63 за акцію, щоб отримати дивіденди безстроково.
