11.5: Кількість ануїтетних платежів
- Page ID
- 66808
Скільки часу ви вимагаєте для виконання мети вашої ануїтету? Все залежить від вашого ануїтетного платежу, процентної ставки та суми залучених грошей.
Зберігаючи на майбутні цілі, багато людей та підприємства просто визначають, скільки вони можуть дозволити собі інвестувати кожен період часу, а потім намагатися бути терплячими, поки вони не досягнуть своєї мети заощаджень. Те, що вони не знають, це скільки часу це займе у них. Якщо ви можете покласти $75 на місяць у свій фонд відпустки, скільки часу знадобиться, щоб заощадити $1,000, необхідні для весняних канікул у Пуерто-Вальярта?
Кредитні картки вимагають невеликої мінімальної оплати щомісяця. Багато канадців розглядають цей мінімальний платіж як пільгу і платять її, не розуміючи, що означає їхнє рішення. Але процентні ставки за кредитними картками складають близько 21% щодня! Таким чином, ви навряд чи можете дозволити собі затримати погашення заборгованості по кредитній карті. Але якщо ви завжди робите тільки мінімальний щомісячний платіж, гасіння $5,000 залишок займе приблизно 50 років!
Очевидно, що кількість ануїтетних платежів має вирішальне значення для фінансових операцій. У цьому розділі ви розраховуєте термін ануїтетів, з'ясувавши кількість необхідних ануїтетних платежів.
Звичайні ануїтети та ануїтети
Розрахувати кількість ануїтетних виплат необхідно в самих різних сценаріях:
- Планування заощаджень
- погашення боргу
- Підтримка зняття коштів з інвестицій
Типова шкала, яка використовується при розрахунку терміну ануїтету, відображається нижче. Нагадаємо, що N не ілюструється на часовій шкалі, а обчислюється за допомогою Формули 11.1 за допомогою Years and\(PY\), які відображаються на часовій шкалі. Частота платежів - це вибір\(PY\), який визначається сторонами, що беруть участь у транзакції, і тому завжди відомий. Це залишає Роки, або термін ануїтету, як невідому змінну на часовій шкалі. Якщо обчислити N, то ви також можете обчислити Роки, використовуючи перестановку Формули 11.1.

В будь-якому кінці часової шкали\(FV_{ORD}\) буде відомий лише один з\(PV_{DUE}\)\(PV_{ORD}\)\(FV_{DUE}\), або.
Формула
Нагадаємо, що кількість ануїтетних виплат\(N\), є однією зі змінних у Формулі 11.2, Формулі 11.3, Формулі 11.4 і Формулі 11.5. Потім обчислення цієї суми вимагає підставити відомі змінні та переставити формулу для вирішення\(N\). Оскільки\(N\) знаходиться в експоненті, перестановка та ізоляція вимагають використання натуральних логарифмів (див. Розділ 2.6). Найскладніше - з'ясувати, яку формулу потрібно використовувати. Виберіть формулу, використовуючи ті самі критерії прийняття рішення, описані в розділі 11.4 (у розділі «Формула»).
Як це працює
Виконайте наступні дії, щоб вирішити кількість ануїтетних платежів або термін ануїтету:
Крок 1: Визначте тип ануїтету. Намалюйте часову шкалу, щоб візуалізувати питання.
Крок 2: Визначте змінні, які завжди з'являються, включаючи\(PMT, IY, CY\), і\(PY\). Ви також повинні визначити одне з відомих значень\(PV_{ORD}\),\(PV_{DUE}\),\(FV_{ORD}\), або\(FV_{DUE}\).
Крок 3: Використовуйте формулу 9.1 для розрахунку\(i\).
Крок 4: Замініть правильну формулу оплати ануїтету, яка відповідає вашому типу ануїтету та відомої теперішньої або майбутньої вартості. Виберіть формулу 11.2, Формулу 11.3, Формулу 11.4 або Формулу 11.5. Переставляйте і вирішуйте для\(N\).
Крок 5: Щоб перетворити\(N\) назад у більш часто виражений формат, наприклад, роки та місяці, візьміть Формулу 11.1 та перевпорядкуйте його на роки. Якщо Роки є десятковим числом, згадайте кроки, необхідні для перетворення на загальну мову з «Цілочисельних періодів складання» на сторінці xx у розділі 9.7.
Важливі зауваження
Робота з десятковими знаками в \(N\)
В кінці кроку 4 розрахункове значення\(N\) може мати десяткові знаки. Почніть з застосування тих же правил округлення, що передбачають обчислення\(N\) для одиничних платежів, подумки округлення десяткового знака до третього знака після коми.
- Якщо три десяткових числа - нулі, то десяткові числа, швидше за все, є результатом округлення\(FV, PV\), або, таким чином\(PMT\), ставитеся до\(N\) подібного цілого числа (ігноруючи десяткові числа).
- Якщо три десяткових знака не всі нулі, то\(N\) слід завжди округлити до наступного цілого числа незалежно від десяткового значення. Ви ніколи не повинні округлити його вниз, тому що розрахункове значення\(N\) являє собою мінімальні необхідні платежі. Тлумачення та наслідки цього округлення такі:
- Виплати за боргом. Припустимо, що ваші платежі по кредиту складають 100 доларів, і ви розраховуєте\(N\) = 9.4, який округляє до 10 платежів. Виплати повинні точно звести кредит до нуля. Перші дев'ять платежів - це все 100 доларів. Останній платіж не є повним платежем, звідси 0,4 в розрахунку. Точний розрахунок цієї останньої суми платежу пояснюється в розділі 13; однак на даний момент достатньо розглядати десяткову кількість як приблизний відсоток від того, яким може бути остаточний платіж. 0.4 становить приблизно 40% від 100 доларів, або 40 доларів. В результаті є дев'ять платежів у розмірі 100 доларів, а один остаточний платіж наближається до 40 доларів. Майте на увазі, що це наближення є грубим у кращому випадку і його слід використовувати лише для того, щоб відчути, якою може бути остаточна сума платежу. Важливим моментом тут є те, що для погашення кредиту повністю потрібно 10 платежів, незалежно від суми платежу.
- Платежі в рахунок інвестицій. Зберігаючи цифри такими ж, як вище, ваші інвестиційні платежі складають 100 доларів з\(N\) = 9.4. Знову ж таки, це 10 платежів. Якщо ви зробите лише дев'ять повних платежів у розмірі 100 доларів, ваші інвестиції не перевищуватимуть запланованої майбутньої вартості. Однак якщо ви дозволите йому рости і зробите десятий повний платіж, у вас буде більше, ніж ваша інвестиційна мета. Що\(N\) = 9.4 говорить вам, що остаточний десятий платіж потрібен приблизно 40% шляху через наступний інтервал оплати, який становить приблизно 0,4 від звичайної суми платежу. Однак більшість інвесторів не дбають про те, щоб зберегти занадто багато грошей і перевищити свою мету заощаджень, тому зазвичай робиться повний десятий платіж.
Речі, на які слід стежити
Дві помилки поширені при розрахунках кількості ануїтетних платежів:
- Неправильне тлумачення\(N\). Плутаність частоти складання (\(CY\)) та частоти оплати (\(PY\)) призводить до неправильного тлумачення\(N\) та неправильного розрахунку терміну. Оскільки\(N\) являє собою кількість ануїтетних платежів, для присвоєння його значення потрібно дивитися на\(PY\), а не на\(CY\). Тоді використовуйте значення\(PY\) у формулі 11.1 при\(N\) вираженні більш поширеними термінами. Наприклад, якщо\(N\) = 8,\(PY\) = 4 і\(CY\) =2, поширеною помилкою є сказати, що існує вісім піврічних платежів (використовуючи\(CY\)); переконайтеся, що ви подивитеся замість цього на\(PY\), ідентифікуючи вісім квартальних платежів, що означає термін два роки.
- Заплутаний термін і останній платіж за ануїтетами до сплати. Однією з характеристик належної ануїтету є те, що останній платіж відбувається за один інтервал платежу до закінчення терміну ануїтету. При розрахунку ви\(N\) розрахували термін ануїтету. Останній платіж відбувається з\(N − 1\) інтервалами від початку ануїтету. Наприклад, припустимо, що платежі є щомісячними, і ви розраховуєте\(N = 12\) місяці. Це означає, що термін ануїтету становить 12 місяців. Останній платіж за доплатою ануїтету становить 12 — 1 = 11 місяців від початку. У своєму «Плані» для будь-якої проблеми обов'язково визнаєте, чи шукаєте ви кінець терміну або коли здійснено останній платіж. Ця проблема не виникає для звичайних ануїтетів, оскільки останній платіж і закінчення терміну припадають на одну дату.
Тримаючи всі інші змінні постійними, що відбувається математично з кількістю платежів (точне розрахункове значення\(N\) виробленого шляхом перестановки будь-якої з ануїтетних формул), якщо відбувається наступне:
- Змінна процентна ставка збільшується (а сам платіж залишається незмінним)?
- Аннуїтетні виплати подвоюються?
- Відповідь
-
- Кількість платежів збільшується, якщо змінна процентна ставка збільшується, оскільки стягується більше відсотків, але платіж не збільшився, щоб покрити більш високі процентні збори.
- Кількість платежів зазвичай скорочується принаймні наполовину, якщо ануїтетні платежі подвоюються, оскільки з кожним платежем основна сума стає меншою за прискореною ставкою і нараховується менше відсотків.
Самія має 500 000 доларів, накопичених у своїх пенсійних накопиченнях, коли вона вирішує вийти на пенсію у віці 60 років. Якщо вона хоче отримувати виплати на початку місяця в розмірі 3000 доларів, а її пенсійний ануїтет може заробляти 5,2% щомісяця, скільки років Самії, коли фонд виснажується?
Рішення
Крок 1:
Виплати знаходяться на початку інтервалів платежів, а період складання та інтервали виплат однакові. Тому це проста рента за рахунок. Шукаючи скільки років Самії буде, коли фонд буде виснажений, підрахуйте кількість ануїтетних виплат, або\(N\), що її пенсійний ануїтет може витримати.
Що ви вже знаєте
Крок 1 (продовження):
Терміни для пенсійного ануїтету відображаються нижче.

Крок 2:
\(PV_{DUE}\)= 500 000 доларів,\(IY\) = 5,2%,\(CY\) = 12,\(PMT\) = 3000 доларів,\(PY\) = 12,\(FV\) = 0
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Підставляємо в Формулу 11.5, переставляючи для\(N\).
Крок 5:
Замініть у формулу 11.1 і вирішуйте Роки. Додайте цей термін до поточного віку Самії, щоб з'ясувати, скільки їй років, коли ануїтет виснажується.
Виконувати
Крок 3:
\[i=5.2 \% \div 12=0.4 \overline{3} \% \nonumber \]
Крок 4:
\[\$ 500,000=\$ 3,000\left[\dfrac{1-\left[\frac{1}{(1+0.0043)^{\frac{12}{12}}}\right]^N}{(1+0.004 \overline{3})^{\frac{12}{12}}-1}\right] \times(1+0.004 \overline{3})^{\frac{12}{12}} \nonumber \]
\[\begin{aligned} 165.947560&=\dfrac{1-0.995685^{N}}{0.0043}\\ 0.995685^{N}&=0.280893 \\ N \times \ln (0.995685)&=\ln (0.280893)\\ N&=\dfrac{-1.2697323}{-0.004323}\\ N&=293.660180 \end{aligned} \nonumber \]
Округлення до 294 щомісячних платежів, що складаються з 293 регулярних платежів плюс один додатковий менший платіж.
Крок 5:
\[294=12 \times \text { Years } \nonumber \]
\[\text { Years }=\dfrac{294}{12}=24.5=24 \text { years, } 6 \text { months } \nonumber \]
Інструкція калькулятора
| Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| ЛВ | Відповідь: 293.660180 | 5.2 | -500000 | 300 | 0 | 12 | 12 |
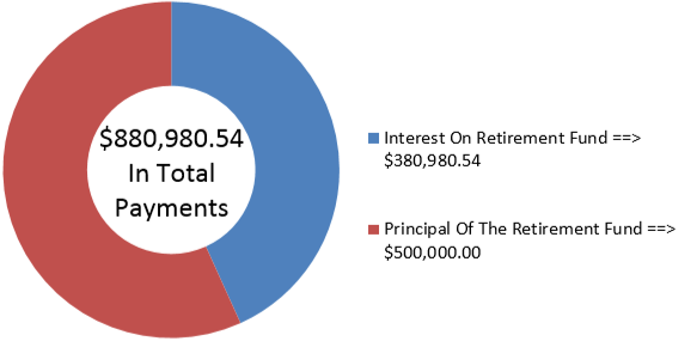
На малюнку видно, скільки основного боргу і відсотків складають виплати. Якщо Самії в даний час 60 років, а ануїтет триває 24 роки і шість місяців, то їй буде 84,5 років, коли ануїтет виснажується. Зверніть увагу, що Samia отримає 293 платежі в розмірі 3000 доларів разом з меншим остаточним платежем, який наближається, приймаючи 66.018% × $3,000 = $1,980,54
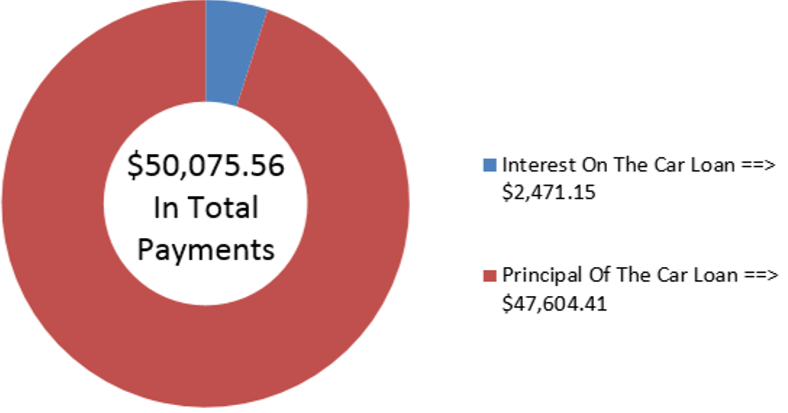
Брендан купує абсолютно новий Mazda MX-5 GT. Включаючи всі варіанти, аксесуари та збори, загальна сума, яку йому потрібно фінансувати, становить $47 604.41 при спеціальному процентному фінансуванні дилера 2.4%, що складається щомісяця. Якщо він здійснює виплати в розмірі 1000 доларів в кінці кожного місяця, скільки часу знадобиться, щоб погасити свій автокредит?
Рішення
Крок 1:
Платежі проходять в кінці інтервалів платежів з щомісячним періодом складання та інтервалами щомісячних платежів. Тому це звичайна проста ануїтет. Розрахувати кількість щомісячних платежів\(N\), або, щоб з'ясувати тривалість часу, необхідного для погашення кредиту.
Що ви вже знаєте
Крок 1 (продовження):
Графік оплати автомобіля відображається нижче.

Крок 2:
\(PV_{ORD}\)= $47 604.41,\(IY\) = 2.4%,\(CY\) = 4,\(PMT\) = 1000$,\(PY\) = 12,\(FV\) = 0
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Підставляємо в Формулу 11.4, переставляючи для\(N\).
Крок 5:
Замініть у формулу 11.1 і вирішуйте Роки.
Виконувати
Крок 3:
\[i=2.4 \% \div 12=0.2 \% \nonumber \]
Крок 4:
\[\begin{aligned} \$ 47,604.41&=\$ 1,000\left[\dfrac{1-\left[\dfrac{1}{(1+0.002)^{\frac{12}{12}}}\right]^{N}}{(1+0.002)^{\frac{12}{12}-1}}\right] \\ 0.095208&=1-0.998003^{N} \\ 0.998003^N&=0.904791\\ N \times \ln (0.998003)&=\ln (0.904791) \\ N&=\dfrac{-0.100051}{-0.001998}\\ &=50.075560 \end{aligned} \nonumber \]
Округлено до 51 щомісячних платежів.
Крок 5:
\[51=12 \times \text { Years } \nonumber \]
\[\text { Years }=\dfrac{51}{12}=4.25=4 \text { years, } 3 \text { months } \nonumber \]
Інструкція калькулятора
| П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|
| Відповідь: 50.075560 | 2.4 | 47604.41 | -1000 | 0 | 12 | 12 |
На малюнку видно, скільки основного боргу і відсотків складають виплати. Щоб володіти своїм транспортним засобом, Брендан буде здійснювати виплати протягом чотирьох з чвертю років. Це складається з 50 платежів у розмірі 1000 доларів США та меншого остаточного платежу, який наближається, приймаючи 7.556% × 1000 доларів = 75.56 доларів.
Тревор хоче заощадити до 1 000 000 доларів. Він буде вносити $5,000 щорічно на інвестиційний заробіток 10% посилюється щомісяця. Яка різниця в часі між його останніми платежами (не закінченням ануїтетів), якщо він робить свої внески наприкінці року, а не на початку року?
Рішення
Крок 1:
У цьому питанні вас просять порівняти два ануїтети, які відрізняються інтервалами платежів та періодами складання. Одна ануїтет вносить внески на початку інтервалу, а інша вносить внески в кінці. Тому ви повинні протиставити один загальний ануїтет через один звичайний загальний ануїтет. Щоб визначити різницю в часі, розрахуйте N для кожного ануїтету і порівняйте, коли проводиться останній платіж.
Що ви вже знаєте
Крок 1 (продовження):
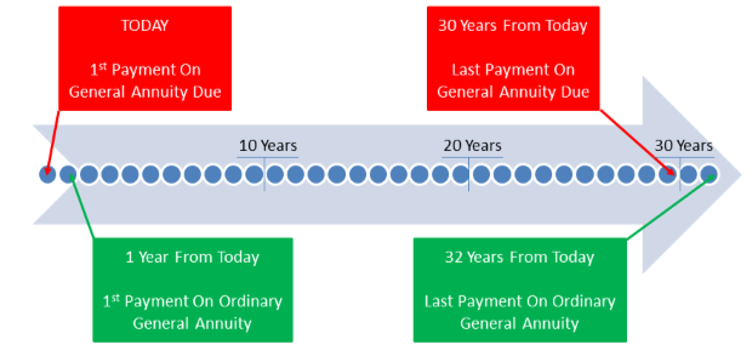
Нижче відображається комбінований графік для двох ануїтетів.

Крок 2:
Звичайний загальний ануїтет:\(FV_{ORD}\) = 1,000,000,\(IY\)\(CY\) = 10%, = 12,\(PMT\) = 5000 доларів,\(PY\) = 1
Загальний ануїтет до сплати:\(FV_{DUE}\) = 1,000,000,\(IY\)\(CY\) = 10%,\(PMT\) = 12, = 5000 доларів,\(PY\) = 1
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Застосуйте Формулу 11.2 і Формулу 11.3, переставляючи для\(N\).
Крок 5:
Якщо виплати щорічні, то\(N\) = Роки. Однак для загальної ренти за рахунок останнього платежу проводиться\(N − 1\) роками з сьогоднішнього дня. Різниця між двома платежами потім може бути розрахована.
Крок 3:
\[i=10 \% \div 12=0.8 \overline{3} \% \nonumber \]
Крок 4:
Звичайний загальний ануїтет:
\[\begin{aligned} \$ 1,000,000&=\$ 5,000\left[\dfrac{\left[(1+0.008 \overline{3})^{\frac{12}{1}}\right]^{N}-1}{(1+0.008 \overline{3})^{\frac{12}{1}}-1}\right]\\ 20.942613&= 1.104713^{N}-1 \\ 21.942613&=1.104713^{N}\\ \ln (21.942613) & = N \times \ln (1.104713) \\ \dfrac{\ln (21.942613)}{\ln (1.104713)}&=N \\ N&=31.012812, \text { or } 32 \text { years } \end{aligned} \nonumber \]
Загальний ануїтет до сплати:
\[\begin{aligned} \$ 1,000,000&=\$ 5,000\left[\dfrac{\left[(1+0.008 \overline{3})^{\frac{12}{1}}\right]^{N}-1}{(1+0.008 \overline{3})^{\frac{12}{1}}-1}\right]\times (1+0.008 \overline{3})^{\frac{12}{1}}\\ 18.957514&= 1.104713^{N}-1 \\ 19.957514&=1.104713^{N}\\ \ln (19.957514) & = N \times \ln (1.104713) \\ \dfrac{\ln (19.957514)}{\ln (1.104713)}&=N \\ N&=30.060618, \text { or } 31 \text { years } \end{aligned} \nonumber \]
Крок 5:
Звичайний загальний ануїтетний останній платіж становить 32 роки з сьогоднішнього дня. Загальний термін погашення ренти становить 31 рік, але останній платіж становить 31 − 1 = 30 років з сьогоднішнього дня. Різниця між останніми платежами становить 32 − 30 = 2 роки раніше. (Дивіться малюнок нижче і порахуйте точки!)
Інструкція калькулятора
| Тип | Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|---|
| Звичайний | Відповідь: 30.060618 | 10 | 0 | -5000 | 1000000 | 1 | 12 | |
| Через | ЛВ | Відповідь: 31.012812 | \(\surd\) | \(\surd\) | \(\surd\) | \(\surd\) | \(\surd\) | \(\surd\) |
Для того, щоб Тревор досяг своєї мети, якби він зробив свої внески в розмірі 5000 доларів на початку року (тобто під належну ануїтет) замість кінця року (за звичайною ануїтетом), його останній платіж був би на два роки раніше. Не плутайте це з умовами двох ануїтетів, які закінчуються лише один рік (31 рік відтепер і 32 роки відтепер).