11.2: Майбутня вартість ануїтетів

Last updated
Save as PDF

Page ID: 66807

Jean-Paul Olivier
Red River College of Applied Arts, Science, & Technology

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Хоча ваш вихід на пенсію, ймовірно, ще далекий шлях, чим раніше ви починаєте інвестувати, тим більше ви можете скористатися силою посилення відсотків, щоб генерувати свої заощадження.

Це здивувало вас дізнатися в розділі 10.5, що ваш річний валовий пенсійний дохід може бути $160,000, коли вам виповниться 65 років? Як довго ти проживеш? Середня тривалість життя Канади становить близько 80 років; якщо ви доживете до цього віку, вам знадобиться 15 років пенсійного доходу. Використовуючи консервативну процентну ставку 5%, що збільшується щорічно разом з 3% річної інфляції, це працює, щоб заощадити приблизно 2 мільйони доларів, коли ви вийдете на пенсію. Непроста мета, чи не так? Ви можете задатися питанням: «Якщо я почну економити $300 на місяць сьогодні, чи вистачить мені?»

Зрозуміло, що важливо знати, скільки коштують ваші ануїтети в майбутньому. Це має значення не тільки для інвестицій, але і для боргів, оскільки більшість підприємств і фізичних осіб погашають свої борги через ануїтетні структури. Після того, як ви зробили кілька ануїтетних платежів, ви можете сказати в будь-який час, скільки ви або ваша компанія все ще повинні по непогашеній заборгованості?

У попередньому розділі ви навчилися розпізнавати основні характеристики ануїтетів, тому тепер ви можете приступати до вирішення будь-якого ануїтету для будь-якої невідомої змінної. Існує чотири формули ануїтету. Цей розділ охоплює перші два, які розраховують майбутні значення як для звичайних ануїтетів, так і для належних ануїтетів. Ці формули вміщують як прості, так і загальні ануїтети.

Звичайні ануїтети

Майбутнє значення будь-якого ануїтету дорівнює сумі всіх майбутніх значень для всіх ануїтетних платежів, коли вони переміщуються до кінця останнього інтервалу платежів. Наприклад, припустимо, що ви будете робити вклади в розмірі 1,000 доларів в кінці кожного року протягом наступних трьох років, щоб інвестиції, що заробляють 10% щорічно. Це звичайний простий ануїтет, оскільки платежі знаходяться в кінці інтервалів, а частоти складання та оплати однакові. Якщо ви хотіли знати, скільки грошей у вас є у ваших інвестиціях після трьох років, на малюнку нижче показано, як ви застосуєте фундаментальну концепцію часової вартості грошей, щоб перенести кожну суму платежу на майбутню дату (фокусну дату) та підсумувати значення, щоб прийти до майбутньої вартості.

$clipboard_ea5453e895fe6040570fa895f74a33fea.png$

Хоча ви можете використовувати цю техніку для вирішення всіх ситуацій ануїтету, обчислення стають все більш громіздкими, оскільки кількість платежів збільшується. У наведеному вище прикладі, що робити, якщо людина замість цього зробила щоквартальні внески в розмірі 250 доларів? Тобто 12 платежів протягом трьох років, в результаті чого 11 окремих майбутніх розрахунків вартості. Або якщо вони здійснювали щомісячні платежі, 36 платежів протягом трьох років призведуть до 35 окремих майбутніх розрахунків вартості! Зрозуміло, що рішення цього було б стомлюючим і трудомістким, не кажучи вже про схильність до помилок. Повинен бути кращий спосіб!

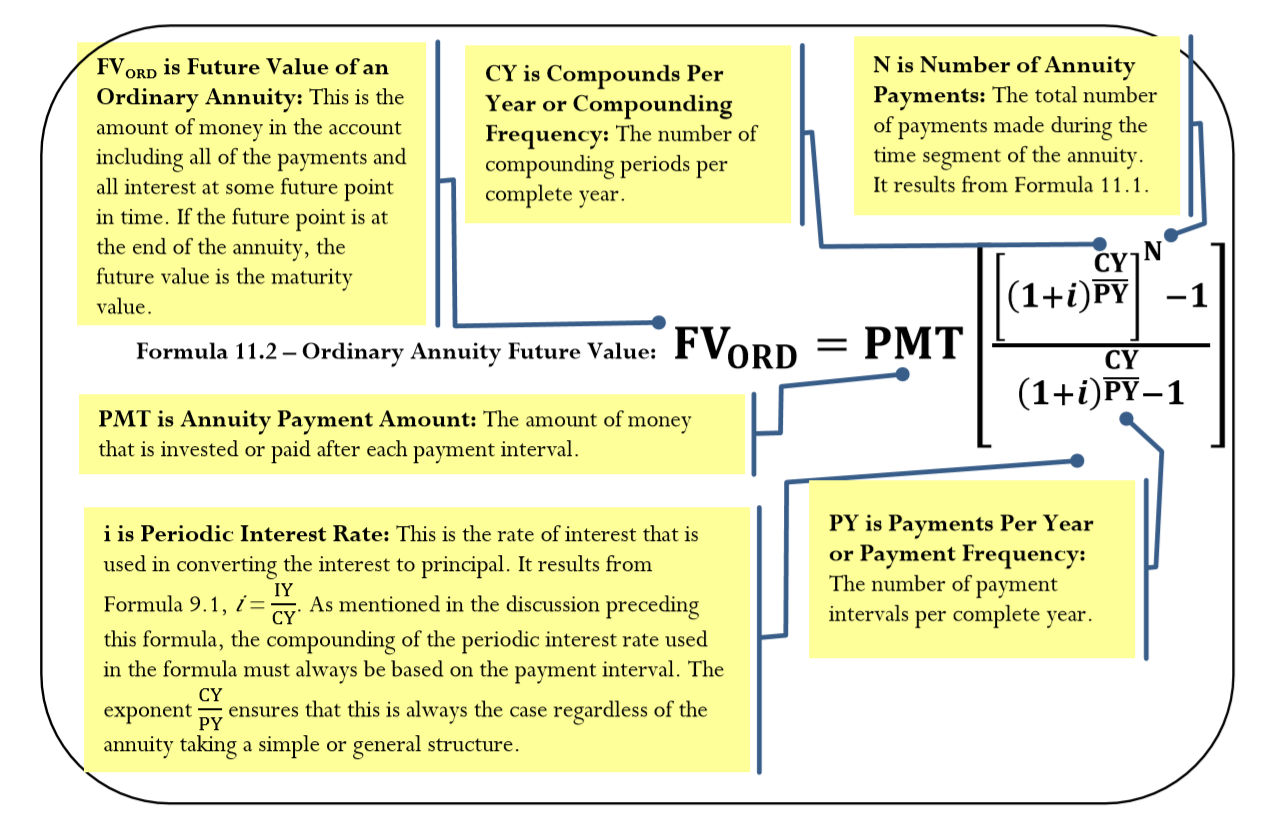
Формула

Формула майбутнього значення звичайної ануїтету дійсно простіше і швидше, ніж виконання ряду майбутніх розрахунків вартості для кожного з платежів. На перший погляд, однак, формула досить складна, тому різні частини формули спочатку вивчаються в деяких деталах, перш ніж ми складемо їх усі разом.

Формула ануїтету - це більш складна версія ставки, порції та базової формули, введеної в главі 2. Відносна Формула 2.2 і перший платіж з наведеної вище цифри дає наступне:

\[\begin{array}{l}{\text { Portion }=\text { Base } \times \text { Rate }} \\ {\$ 1,210=\$ 1,000 \times(1+0.1)^{2}}\end{array} \nonumber \]

T він частина дорівнює майбутньої вартості, а база дорівнює сумі ануїтетного платежу. Ставка виражається у вигляді формули і записується як$(1 + 0.1)^2$. Однак зауважте, що кожен платіж на малюнку має різний показник для відображення необхідного складання. Для цього потрібна математична адаптація$(1 + i)^N$, яка дозволяє визначити еквівалентну ставку, що представляє всі виплати в єдиному розрахунку.

Ця еквівалентна ставка виявляється досить складним виразом, яке розглядається з трьох частин: загальна зміна відсотків, зміна відсотків з кожним платежем та їх частка.

Чисельник - Загальний відсоток зміни:$\left[(1+i)^{\frac{CY}{PY}}\right]^{N}-1$. Ця частина формули визначає зміну відсотків від початку ануїтету до кінця ануїтету. Він має три критичні елементи:
1. Конвертація процентної ставки$(1+i)^{\frac{CY}{PY}}$. Ставка відсотків, яка виникає при кожному платежі, повинна бути відома. Всі ануїтетні розрахунки вимагають, щоб період складання дорівнював інтервалу виплат. Якщо це ще не так, то ви повинні конвертувати виражену процентну ставку в еквівалентну процентну ставку.
  - Для простих ануїтетів конвертація не потрібна, оскільки частоти однакові:$CY = PY$. Показник$\dfrac{CY}{PY}$ завжди дорівнює 1 і не впливає.
  - Для загальних ануїтетів нагадаємо Формулу 9.4 для розрахунку еквівалентних процентних ставок. Тут стара частота компаундирования утворює чисельник ($CY_{Old}$), а нова частота компаундирования (яка відповідає частоті виплат) утворює знаменник ($CY_{New}) = PY$. Таким чином$\dfrac{CY_{OLD}}{PY_{New}}$ стає$\dfrac{CY}{PY}$.
2. Складання$N$. Показник складає періодичну процентну ставку (яка відповідає інтервалу виплат) відповідно до кількості$N$ здійснених ануїтетних платежів. Наприклад, припустимо, що існують дві виплати на кінець року на 10%, що складаються півроку. Якщо процентну ставку залишають піврічно, протягом двох років існує чотири з'єднання, які не відповідають виплатам. Процентна ставка конвертується в дужках від 10%, що складається піврічно, до еквівалентної 10,25% складених щорічних ставок. Кінцевим результатом є те, що відсотки тепер будуть складатися двічі протягом двох років, що відповідає кількості платежів.
3. Вилучення початкової точки (−1). Оскільки ви додали 1 для виконання компаундування, математично вам тепер потрібно видалити 1. Кінцевим результатом є те, що тепер ви знаєте (у десятковому форматі), наскільки більше майбутнє значення щодо його початкового значення.
Знаменник - Зміна відсотків з кожним платежем:$(1+i)^{\frac{CY}{PY}}-1$. Знаменник у формулі показує зміну відсотків на рахунку при кожному здійсненому платежі. Це також гарантує, що знаменник має періодичну ставку, що відповідає інтервалу оплати.
Частка: Беручи чисельник і діливши на знаменник, загальна зміна відсотків ділиться на зміну відсотків з кожним платежем. Це встановлює співвідношення між тим, що відбувається в цілому в ануїтет, і тим, що відбувається з кожною угодою. Таким чином, цей розрахунок визначає, наскільки більша кінцева вартість щодо того, що відбувається з кожним платежем. Цей коефіцієнт (ставка) потім множиться на ануїтетний платіж (базовий), щоб отримати остаточний баланс (частину). Тепер ви в змозі побачити цілу формулу, за якою ви розраховуєте майбутню вартість будь-якого звичайного ануїтету. Ця єдина формула застосовується незалежно від кількості внесених платежів. Формула 11.2 підсумовує змінні та необхідні розрахунки.

$clipboard_e9325ff109d13051cb3d9b68d06fe02bc.png$

Формула 11.2

Як це працює

Існує п'ятикроковий процес розрахунку майбутньої вартості будь-якого звичайного ануїтету:

Крок 1: Визначте тип ануїтету. Намалюйте часову шкалу, щоб візуалізувати питання.

Крок 2: Визначте відомі змінні, включаючи$PV, IY, CY, PMT, PY$, і Years.

Крок 3: Використовуйте формулу 9.1 для розрахунку$i$.

Крок 4: Якщо$PV$ = $0, перейдіть до кроку 5. Якщо є ненульове значення для$PV$, поводьтеся з ним як до єдиного платежу. Застосовуйте формулу 9.2, щоб визначити,$N$ оскільки це не розрахунок ануїтету. Перемістіть теперішнє значення до кінця часового відрізка за допомогою Формули 9.3.

Крок 5: Використовуйте формулу 11.1 для обчислення N для ануїтету. Застосовуємо формулу 11.2 для обчислення майбутнього значення. Якщо ви розрахували майбутнє значення на кроці 4, об'єднайте майбутні значення з кроків 4 та 5, щоб отримати загальну майбутню вартість.

Перегляньте сценарій RRSP з початку цього розділу, припустимо, що вам 20 років і інвестуйте 300 доларів наприкінці кожного місяця протягом наступних 45 років. Ви раніше не розпочали RRSP і не маєте початкового балансу. Можлива фіксована процентна ставка 9%, що складається щомісяця на РРСП.

Крок 1: Це простий звичайний ануїтет, оскільки частоти збігаються, а платежі знаходяться в кінці інтервалу оплати.

$clipboard_e3f133f27024b236990cf7bb417a4a682.png$

Крок 2: Відомі змінні$PV$ = $0,$IY$ = 9%,$CY$ = 12,$PMT$ = $300,$PY$ = 12, і Роки = 45.

Крок 3: Періодична процентна ставка$i$ = 9% ÷ 12 = 0,75%.

Крок 4: Оскільки$PV$ = $0, пропустіть цей крок.

Крок 5: Кількість платіжних тентів$N$ = 12 × 45 = 540. Застосування формули 11.2 дає наступне:

\[FV_{ORD}=\$ 300\left[\dfrac{\left[(1+0.0075)^{\frac{12}{12}}\right]^{540}-1}{(1+0.0075)^{\frac{12}{12}}-1}\right]=\$ 2,221,463.54 \nonumber \]

Отже, 540 виплат у розмірі 300 доларів США на 9%, що складаються щомісяця, призводить до загальної економії $2,221 463.54 за віком виходу на пенсію.

Важливі примітки

Розрахунок суми відсотків. Для інвестиційних ануїтетів, якщо вам цікаво знати, скільки майбутньої вартості є основною і скільки відсотків, ви можете адаптувати Формулу 8.3, де$I = S – P = FV – PV$.

$FV$Це рішення Формули 11.2.
The$PV$ є основною (загальна сума внесків) обчислюється шляхом прийняття$N × PMT + PV$. На малюнку вище,$N × PMT + PV$ = 540 платежів × $300 + $0 = $162 000 в принципі. Отже,$I$ =2,221 463.54 − $162,000 = $2,059 463,54, що є заробленими відсотками.

Ваш калькулятор BAII+. Адаптація навичок калькулятора відповідно до ануїтетів вимагає трьох важливих змін:

У вас тепер є значення для PMT. Обов'язково введіть його з правильним знаком грошового потоку умовності. Коли ви інвестуєте, платіж має той же знак, що і$PV$. Коли ви берете позику, знак платежу протилежний знаку$PV$.
T він P/Y більше не автоматично встановлюється на те саме значення, що і C/Y. введіть свої значення для P/Y і C/Y окремо. Якщо значення однакові, як у випадку з простими ануїтетами, то скориставшись функцією «Копіювати» на калькуляторі, ви уникнете необхідності вводити значення в два рази.
Якщо задіяно теперішнє значення ($PV$), за формулою потрібно зробити два обчислення за допомогою Формули 9.3 і Формули 11.2. Якщо вводити значення для обох$PV$ і$PMT$, калькулятор робить ці обчислення одночасно, вимагаючи лише однієї послідовності для вирішення.

Речі, на які слід стежити

У багатьох ситуаціях ануїтету може виявитися більше однієї невідомої змінної. Зазвичай додаткові невідомі змінні - це «невизначені» змінні, які можна розумно припустити. Наприклад, на ілюстрації RRSP вище можна опустити твердження «ви не розпочали RRSP раніше і не маєте початкового балансу». Якби щось вже було збережено, номер потрібно було б вказати. Як інший приклад, нормально закінчити позику з нульовим залишком. Тому в ситуації з кредитом можна сміливо вважати, що майбутня вартість дорівнює нулю, якщо не вказано інше.

Шляхи до успіху

Можливість розпізнавати простий ануїтет може дозволити спростити Формулу 11.2. Оскільки CY = PY, ці дві змінні утворюють частку 1 для показника. Для простого ануїтету ви можете спростити будь-які виступи наступних алгебраїчних виразів у будь-якій формулі ануїтету (не лише Формула 11.2) наступним чином:

$(1+i)^{\frac{CY}{PY}}$в e чисельник можна спростити до$1+i$

$(1+i)^{\frac{CY}{PY}}-1$в знаменнику можна спростити просто$i$

Таким чином, лише для простих ануїтетів ви спрощуєте Формулу 11.2 як\[FV_{ORD}=PMT\left[\dfrac{(1+i)^{N}-1}{i}\right] \nonumber \]

Вправа$\PageIndex{1}$: Give It Some Thought

Припустимо, ви планували зробити 10 ануїтетних платежів до інвестиції. Однак перед тим, як ви почали платити за інвестиції, ви передумали, подвоївши початкову суму платежу, одночасно роблячи 10 платежів. Що відбувається з вартістю погашення вашої нової інвестиції порівняно з вартістю вашого початкового плану? Чи буде ваш новий баланс рівно подвійним, більш ніж подвійним або менш ніж подвійним? Поясніть і обґрунтуйте свою відповідь.

Відповідь: Ваш новий баланс буде рівно подвійним. Математично ви взяли PMT у Формулі 11.2 і помножили його на 2. Це єдина різниця між вашим початковим планом і новим планом. Тому майбутнє значення також подвоїться.

Приклад$\PageIndex{1}$: Future Value of an Investment Account

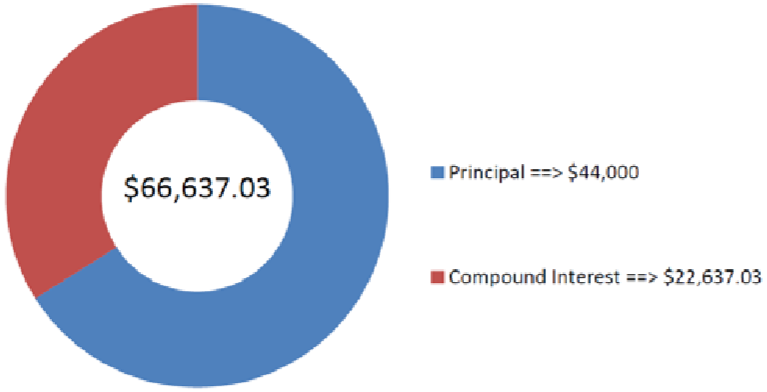
Фінансовий консультант переглядає один з рахунків свого клієнта. Протягом останніх 11 років клієнт інвестував 1000 доларів США наприкінці кожного кварталу у фонд, який щоквартально складав в середньому 7,3%. Скільки грошей у клієнта сьогодні на своєму рахунку?

Рішення

Крок 1:

Платежі знаходяться в кінці інтервалів платежів, і як період складання, так і інтервали платежів однакові. Це звичайна проста ануїтет. Обчисліть його значення в кінці, яке є його майбутнім значенням, або$FV_{ORD}$.

Що ви вже знаєте

Крок 1 (продовження):

На часовій шкалі відображається рахунок клієнта.

$clipboard_e0ca7a77219c91c5deb7c4115f6d18431.png$

Крок 2:

$PV$= 0$,$IY$ = 7,3%,$CY$ = 4,$PMT$ = 1000$,$PY$ = 4, років = 11

Як ви туди потрапите

Крок 3:

Застосувати формулу 9.1.

Крок 4:

Пропустіть цей крок, оскільки$PV$ = $0.

Крок 5:

Застосовуємо Формулу 11.1 і Формулу 11.2.

Виконувати

Крок 3:

$i=7.3 \% \div 4=1.825 \%$

Крок 5:

$N=4 \times 11=44$платежі

\[FV_{ORD}=\$ 1000\left[\dfrac{\left[(1+0.01825)^{\frac{4}{4}}\right]^{44}-1}{(1+0.01825)^{\frac{4}{4}}-1}\right]=\$ 66,637.03 \nonumber \]

Інструкція калькулятора

П	В/У	ПВ	PMT	ФВ	П/У	С/У
44	7.3	0	-1000	Відповідь: 66,637.03449	4	4

На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Після 11 років щоквартальних внесків у розмірі 1000 доларів, клієнт має $66 637,03 на рахунку.

$clipboard_e7607b1ed1f051522f8d7d3e6980dc596.png$

Приклад$\PageIndex{2}$: Future Value of a Savings Annuity

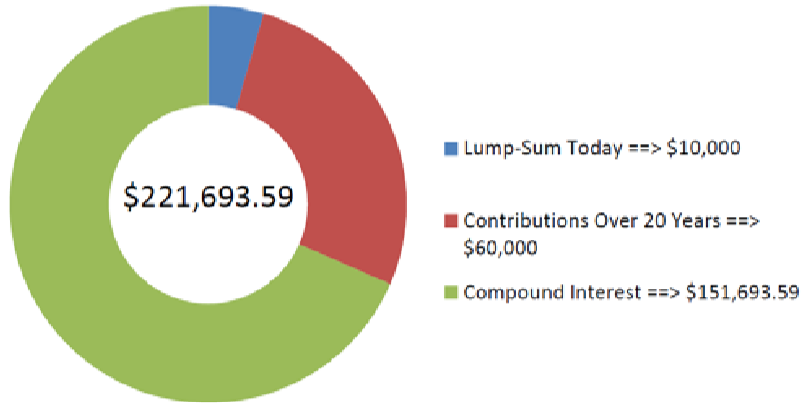
Ощадний ануїтет вже містить $10,000. Якщо додаткові $250 інвестуються наприкінці кожного місяця на 9%, що складаються півроку на термін 20 років, якою буде вартість інвестицій?

Рішення

Крок 1:

Платежі знаходяться в кінці інтервалів платежів, а період складання та інтервали платежів різні. Це звичайна загальна ануїтет. Обчисліть його значення в кінці, яке є його майбутнім значенням, або$FV_{ORD}$.

Що ви вже знаєте

Крок 1 (продовження):

Шкала часу відображається нижче.

$clipboard_e07de49d4ae1ab366d28c04b74c5ae9a4.png$

Крок 2:

$PV$= $10,000,$IY$ = 9%,$CY$ = 2,$PMT$ = 250$,$PY$ = 12, років = 20

Як ви туди потрапите

Крок 3:

Застосувати формулу 9.1.

Крок 4:

Застосовуйте формулу 9.2 та формулу 9.3.

Крок 5:

Застосовуємо Формулу 11.1 і Формулу 11.2 Остаточне майбутнє значення - це сума відповідей на крок 4 ($FV$) і крок 5 ($FV_{ORD}$).

Крок 3:

$i=9 \% \div 2=4.5 \%$

Крок 4:

$N=2 \times 20=40$сполуки

\[FV=\$ 10,000(1+0.045)^{40}=\$ 58,163.64538 \nonumber \]

Крок 5:

$N=12 \times 20=240$платежі

\[FV_{ORD }=\$ 250\left[\dfrac{\left[(1+0.045)^{\frac{2}{12}}\right]^{240}-1}{(1+0.045)^{\frac{2}{12}}-1}\right]=\$ 163,529.9492 \nonumber \]

\[\text {Total }FV=\$ 58,163.64538+\$ 163,529.9492=\$ 221,693.59 \nonumber \]

Інструкція калькулятора

П	В/У	ПВ	PMT	ФВ	П/У	С/У
240	9	-10000	-250	Відповідь: 221 693.5946	12	2

На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Ощадний ануїтет матиме баланс у розмірі 221 693.59 доларів після 20 років.

$clipboard_e38dbb8d94b9c591452eba515b219d643.png$

Важливі примітки

Якщо будь-яка зі змінних, включаючи$IY, CY, PMT$, або$PY$, змінюється між початковою та кінцевою точкою ануїтету, або якщо буде зроблений додатковий депозит або зняття одноразового платежу, створюється новий часовий сегмент, який повинен розглядатися окремо. Потім буде кілька часових відрізків, які вимагають від вас працювати зліва направо, повторюючи кроки з 3 по 5 в процедурі. Майбутнє значення в кінці одного часового відрізка стає теперішнім значенням у наступному часовому відрізку. Приклад$\PageIndex{3}$ ілюструє це поняття.

Речі, на які слід стежити

Зверніть особливу увагу, коли змінною, яка змінюється між часовими відрізками, є частота платежів ($PY$). При введенні в калькулятор$PY$ BAII+автоматично копіюється на частоту складання ($CY$). Якщо ваш$CY$ також не змінився на ту саму частоту, це означає, що ви повинні прокрутити вниз до вікна CY і знову ввести правильне значення для цієї змінної, навіть якщо воно не змінилося.

Шляхи до успіху

При роботі з декількома часовими відрізками важливо, щоб ви завжди починали свої обчислення на стороні навпроти невідомої змінної. Для майбутніх розрахунків вартості це означає, що ви починаєте з лівого боку вашої шкали часу; для розрахунків поточної вартості почніть з правого боку.

Приклад$\PageIndex{3}$: Saving Up for a Vacation

Женев'єва вирішила почати збирати на канікули через два роки, коли закінчить університет. Вона вже має 1000 доларів, зекономлених сьогодні. Протягом першого року вона планує зробити внески в кінці місяця в розмірі 300 доларів, а потім перейти на вклади в кінці кварталу в розмірі 1000 доларів на другий рік. Якщо на рахунку можна заробляти 5% в сукупності півроку в перший рік і 6% щоквартально на другому році, скільки грошей вона заощадить, коли закінчить навчання?

Рішення

Крок 1:

Відбувається зміна змінних через рік. Як результат, вам потрібен часовий відрізок року 1 та часовий відрізок року 2. В обох сегментах виплати припадають на кінець періоду. У 1-му році період складання та інтервали виплат різні. У 2-му році період складання та інтервали виплат однакові. Це звичайна загальна ануїтет, за якою слідує звичайна проста ануїтет. Ви прагнете обчислити майбутнє значення, або$FV_{ORD}$.

Що ви вже знаєте

Крок 1 (продовження):

Графік її заощаджень на відпустці відображається нижче.

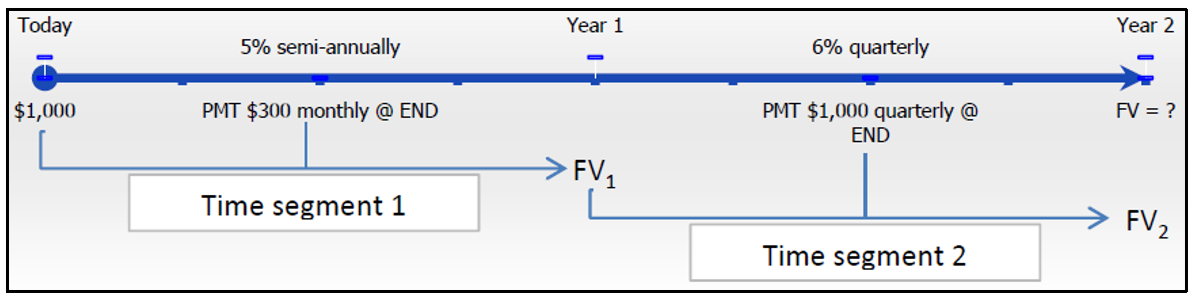
$clipboard_ee0633e04eea454f10574454edac3f1a4.png$

Крок 2:

Часовий відрізок 1:$PV$ = 1000$,$IY$$CY$ = 5%, = 2,$PMT$ = 300$,$PY$ = 12, років = 1

Часовий відрізок 2:$PV = FV_1$ часового відрізка 1,$IY$$CY$ = 6%,$PMT$ = 4, = 1000$,$PY$ = 4, років = 1

Як ви туди потрапите

Для кожного часового відрізка повторіть наступні дії:

Крок 3:

Застосувати формулу 9.1.

Крок 4:

Застосовуйте формулу 9.2 та формулу 9.3.

Крок 5:

Застосовуємо Формулу 11.1 і Формулу 11.2. Загальне майбутнє значення в будь-якому часовому відрізку - це сума відповідей на крок 4 ($FV$) і крок 5 ($FV_{ORD}$).

Виконувати

Вперше сегмент:

Крок 3:

$i=5 \% \div 2=2.5 \%$

Крок 4:

$N=2 \times 1=2$сполуки

\[FV_{1}=\$ 1,000(1+0.025)^{2}=\$ 1,050.625 \nonumber \]

Крок 5:

$N=12 \times 1=12$платежі

\[FV_{ORD1}=\$ 300\left[\dfrac{\left[(1+0.025)^{\frac{2}{12}}\right]^{12}-1}{(1+0.025)^{\frac{2}{12}}-1}\right]=\$ 3,682.786451 \nonumber \]

\[\text {Total } FV_{1}=\$ 1,050.625+\$ 3,682.786451=\$ 4,733.411451 \nonumber \]

Для другого сегмента часу:

Крок 3:

$i=6 \% \div 4=1.5 \%$

Крок 4:

$N=4 \times 1=4$сполуки

\[FV_{2}=\$ 4,733.411451(1+0.015)^{4}=\$ 5,023.870384 \nonumber \]

Крок 5:

$N=4 \times 1=4$платежі

\[FV_{ORD2}=\$ 1,000\left[\dfrac{\left((1+0.015)^{\frac{4}{4}}\right]^{4}-1}{(1+0.015)^{\frac{4}{4}}-1}\right]=\$ 4,090.903375 \nonumber \]

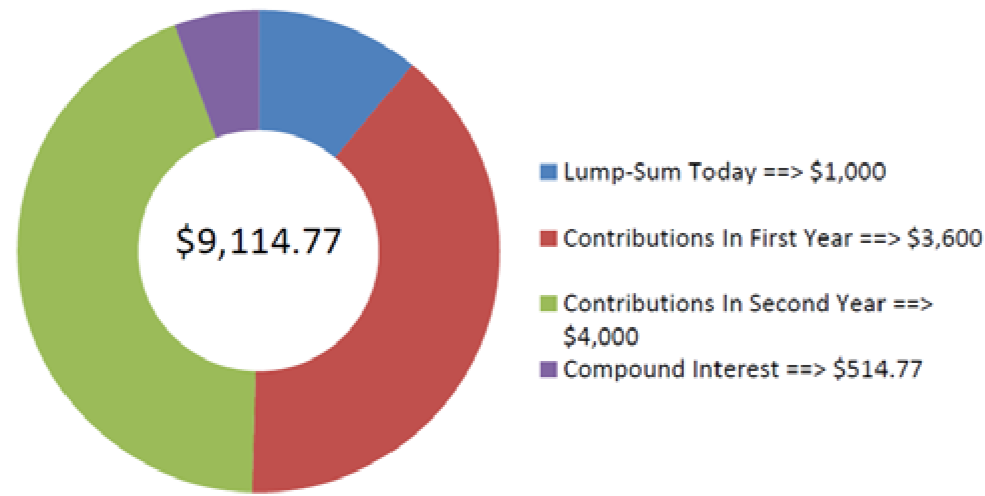
\[\text { Total } FV_{2}=\$ 5,023.870384+\$ 4,090.903375=\$ 9,114.77 \nonumber \]

Інструкція калькулятора

Часовий відрізок	П	В/У	ПВ	PMT	ФВ	П/У	С/У
1	12	5	-1000	-300	Відповідь: 4,733.411451	12	2
2	4	6	-4 733,411451	-1000	Відповідь: 9,114.773759	4	4

На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Коли Женев'єва закінчить, вона заощадить 9 114,77 доларів на свою відпустку.

$clipboard_e03e3999e0dd95844fe4574678edeefd3.png$

Ануїтети до оплати

Ануїтет настає при здійсненні виплат на початку платіжного інтервалу. Щоб зрозуміти різницю, яку це робить для майбутнього значення, давайте перерахуємо приклад RRSP з раніше в цьому розділі, але розглядаємо це як належну ренту. Ви хочете знати майбутню вартість внесення $1,000 щорічних внесків на початку кожного інтервалу платежів протягом наступних трьох років до інвестиційного заробітку 10% щорічно. Це формує просту ренту за рахунок. На малюнку нижче показано, як ви застосовуєте фундаментальну концепцію часової вартості грошей, щоб перенести кожну суму платежу на майбутню дату (фокусну дату) та підсумувати значення, щоб прийти до майбутньої вартості.

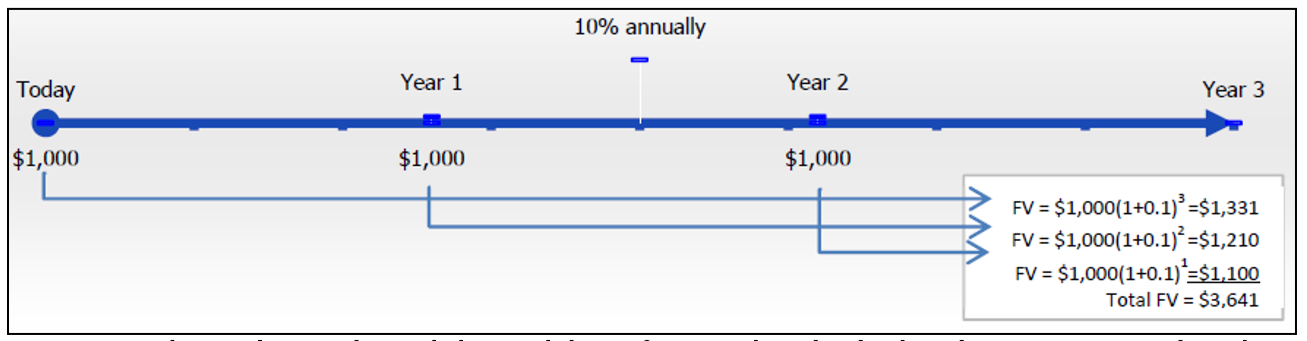
$clipboard_e5082d9f61c341a9d56119dfa43a764d2.png$

Зверніть увагу, що ви не закінчите з однаковим балансом у розмірі 3,310 доларів, досягнутим за звичайним ануїтетом. Натомість у вас є більший баланс у розмірі 3,641 доларів. Чому це? Розміщення двох типів ануїтетів поруч один з одним на наступному малюнку демонструє ключову різницю між двома прикладами.

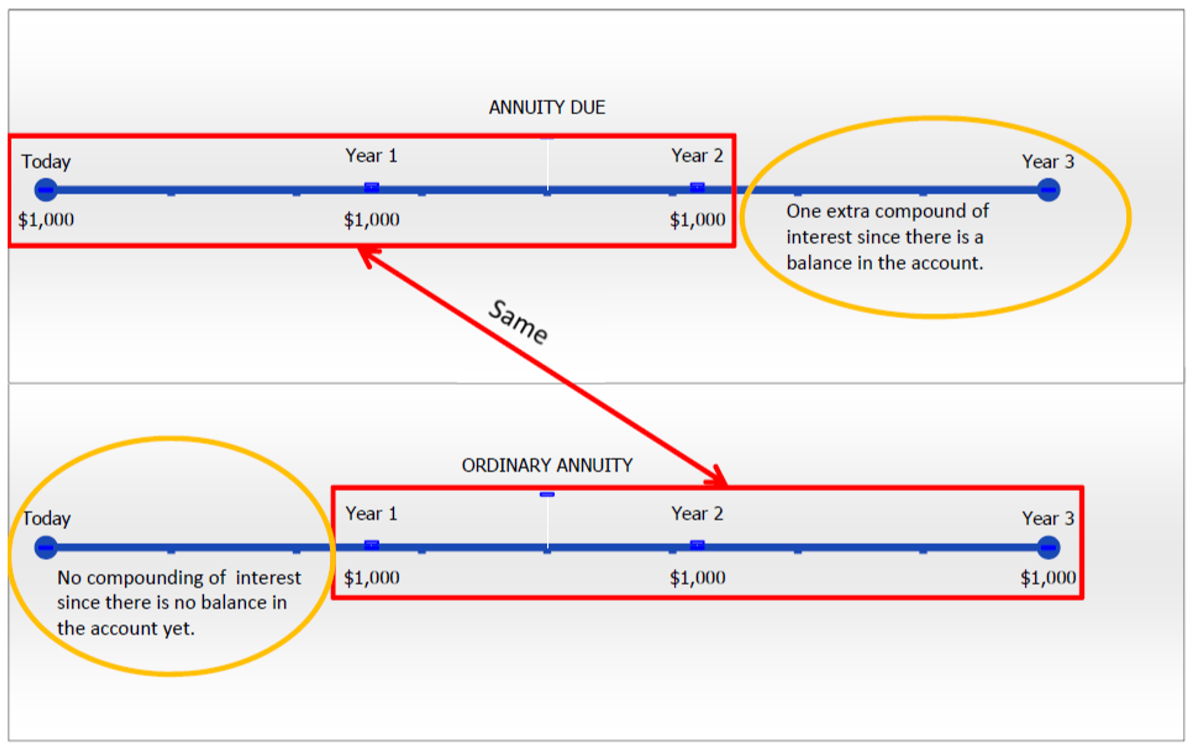
$clipboard_e52f701b3650936cc996a150f38082dc1.png$

Обидва ануїтети мають однакову послідовність трьох платежів у розмірі 1000 доларів. Однак в звичайному ануїтеті ніякі відсотки не нараховуються протягом першого інтервалу платежу, оскільки основна сума дорівнює нулю, а виплата не відбувається до кінця інтервалу. З іншого боку, в ануїтет через додатковий склад відсотків заробляється в останньому інтервалі виплат через існуючий основний капітал в кінці другого року. Якщо взяти остаточний баланс звичайного ануїтету в $3,310 і дати йому один додатковий склад у вас є$FV$ = $3,310 (1 + 0.1) = $3,641. Підсумовуючи, ключова відмінність між двома типами ануїтетів полягає в тому, що ануїтет, належний завжди отримує один додатковий склад відсотків.

Формула

Адаптація звичайної ануїтетної формули майбутнього значення відповідно до додаткової сполуки створює Формулу 11.3. Зверніть увагу, що всі змінні у формулі залишаються однаковими; однак індекс на символі FV змінюється, щоб розпізнати різницю в необхідному обчисленні.

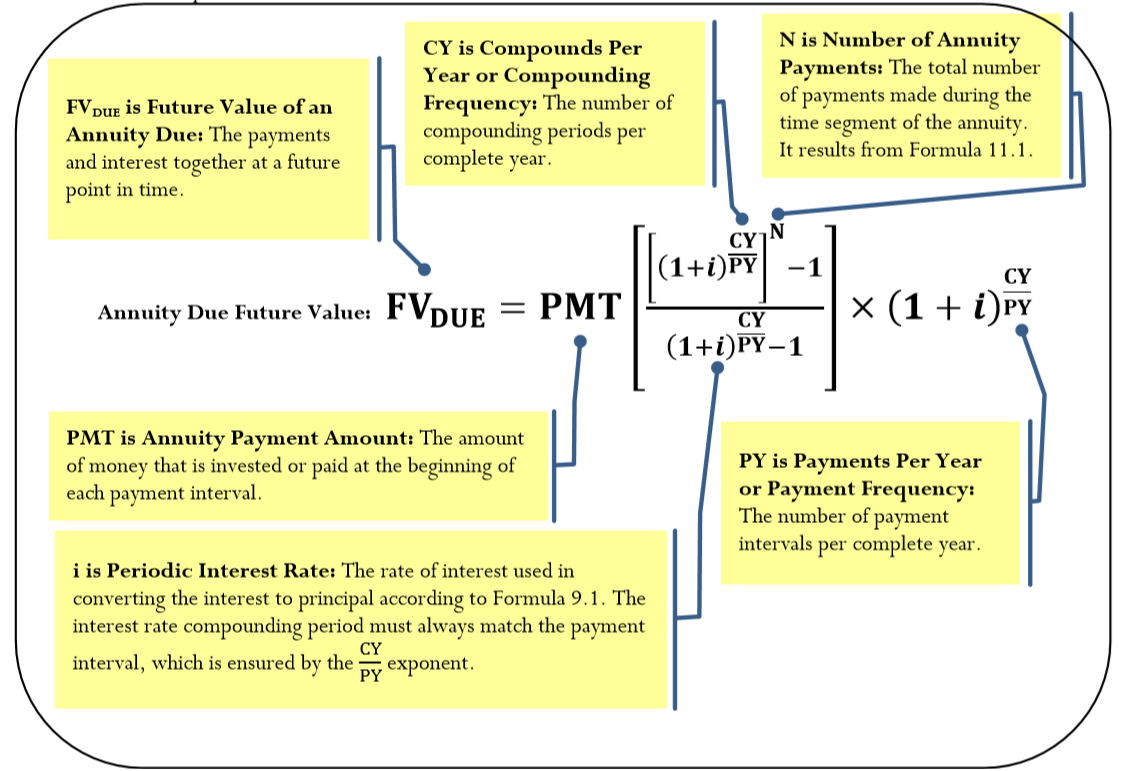
$clipboard_eed19f1c55204c836233566fc43c5cb4b.png$

Формула 11.3

Як це працює

Кроки, необхідні для вирішення для або майбутньої вартості ануїтету належної майже ідентичні тим, які ви використовуєте для звичайного ануїтету. Єдина відмінність полягає в кроці 5, де замість Формули 11.2 використовується Формула 11.3. Приклад$\PageIndex{4}$ і приклад$\PageIndex{5}$ ілюструють адаптацію.

Важливі примітки

$clipboard_ed30ed6eae32288d29b2ce638b58cfcda.png$

Щоб адаптувати калькулятор до ануїтету, потрібно перемкнути налаштування часу платежу від END до BGN. Калькулятор за замовчуванням - END, який є звичайним ануїтетом. Налаштування часу оплати знаходиться на другій полиці над ключем PMT (оскільки це пов'язано з PMT!). Щоб увімкнути налаштування, виконайте наступну послідовність:

2nd BGN (відображається поточний час оплати END або BGN)
2nd SET (перемикає іншу настройку)
2-й Вихід (щоб вийти з вікна)

Коли калькулятор знаходиться в режимі ануїтету, крихітний BGN з'являється у верхньому правому куті вашого калькулятора. Щоб повернути калькулятор в звичайний режим, повторіть описане вище

Вправа$\PageIndex{2}$: Give It Some Thought

За рівних умов

Для будь-яких інвестицій, які завжди матимуть вищу майбутню вартість: звичайний ануїтет або належний ануїтет? Поясніть.
Для будь-якого боргу, який завжди буде мати більш високу майбутню вартість: звичайний ануїтет або належний ануїтет? Поясніть.

Відповідь

Ануїтет за рахунок матиме вищу майбутню вартість, оскільки вона завжди має одне додаткове з'єднання порівняно зі звичайним ануїтетом.
Звичайний ануїтет матиме вищу майбутню вартість, оскільки основна сума в першому інтервалі виплат вище і, отже, нараховується більше відсотків, ніж у належному ануїтетному.

Приклад$\PageIndex{4}$: Lottery Winnings

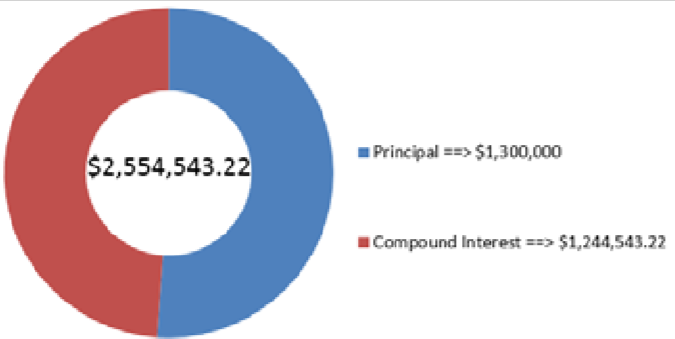
Миттєвий квиток Set for Life Scratch n 'win пропонує гравцям шанс виграти $1,000 на тиждень протягом наступних 25 років, починаючи відразу після перевірки. Якби переможець інвестував усі свої гроші на рахунок, який заробляє 5% щорічно, скільки грошей він мав би наприкінці свого 25-річного терміну? Припустимо, що кожен рік має рівно 52 тижні.

Рішення

Крок 1:

Виплати починаються негайно, а період складання та інтервали платежів різні. Тому це загальна рента за рахунок. Обчисліть його значення в кінці, яке є його майбутнім значенням, або$FV_{DUE}$.

Що ви вже знаєте

Крок 1 (продовження):

Хронологія заощаджень лотереї наведена нижче.

$clipboard_e1c386c8ab04305ae601501f9987abea6.png$

Крок 2:

$PV$= 0$,$IY$ = 5%,$CY$ = 1,$PMT$ = 1000$,$PY$ = 52, років = 25

Як ви туди потрапите

Крок 3:

Застосувати формулу 9.1.

Крок 4:

Пропустіть цей крок, оскільки немає$PV$.

Крок 5:

Застосуйте Формулу 11.1 і Формулу 11.3.

Виконувати

Крок 3:

$i=5 \% \div 1=5 \% $

Крок 5:

$N=52 \times 25=1,300$платежі

\[\begin {aligned}FV_{DUE}&=\$ 1,000\left[\dfrac{\left[(1+0.05)^{\frac{1}{52}}\right]^{1300}-1}{(1+0.05)^{\frac{1}{52}}-1} \times(1+0.05)^{\frac{1}{52}}\right]\\&=\$2,544,543.22 \end{aligned} \nonumber \]

Інструкція калькулятора

Режим	П	В/У	ПВ	PMT	ФВ	П/У	С/У
ЛВ	1300	5	0	-1000	Відповідь: 2,544 543.218	52	1

На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Якщо переможець повинен був інвестувати всі свої призові гроші лотереї, він мав би $2,544,543.22 через 25 років.

$clipboard_e39532acd38efc66d09b932fb1b5f7721.png$

Приклад$\PageIndex{5}$: Saving into a Trust Fund with a Variable Change

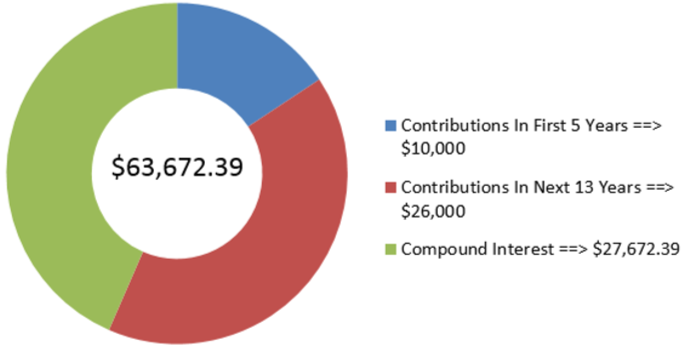
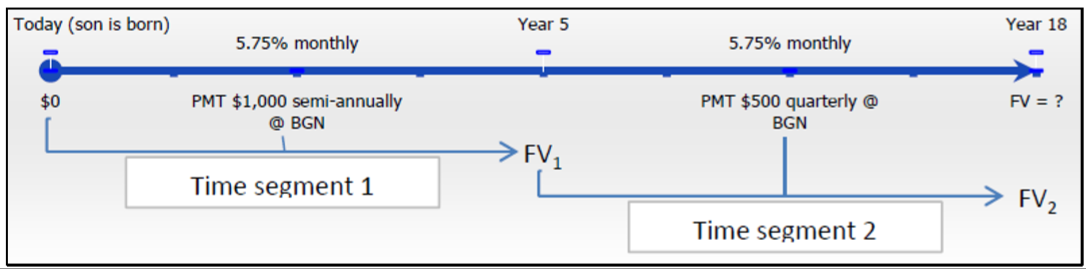
Коли народився син Роберто, Роберто почав робити виплати в розмірі 1000 доларів на початку кожні шість місяців до цільового фонду, що заробляє 5,75% щомісяця. Через п'ять років він змінив свої внески і почав вносити 500 доларів на початку кожного кварталу. Скільки грошей буде в цільовому фонді сина, коли синові виповниться 18 років?

Рішення

Крок 1:

Відбувається зміна змінних через п'ять років. В результаті потрібно два часових відрізка. В обох сегментах платежі знаходяться на початку періоду, а періоди складання та інтервали виплат різні. Тому Роберто має два послідовних загальних ануїтетів. Комбіновані, обчислюють майбутню величину, або$FV_{DUE}$.

Що ви вже знаєте

Крок 1 (продовження):

Графік роботи цільового фонду наведено нижче.

$clipboard_e48220fd641e5ca182addee627e0ead0b.png$

Крок 2:

Часовий відрізок 1:$PV$ = 0$,$IY$ = 5,75%,$CY$ = 12,$PMT$ = 1000$,$PY$ = 2, років = 5

Часовий відрізок 2:$PV = FV_1$ часового відрізка 1,$IY$$CY$ = 5,75%,$PMT$ = 12, = 500$,$PY$ = 4, років = 13

Як ви туди потрапите

Для кожного часового відрізка повторіть наступні дії:

Крок 3:

Застосувати формулу 9.1.

Крок 4:

Якщо є$PV$, застосуйте Формулу 9.2 і Формулу 9.3.

Крок 5:

Застосуйте Формулу 11.1 і Формулу 11.3. Загальне майбутнє значення в будь-якому часовому відрізку - це сума відповідей на крок 4 ($FV$) і крок 5 ($FV_{ORD}$).

Виконувати

Крок 3:

$i=5.75 \% \div 12=0.4719 \overline{6} \%$

Крок 4:

Ні$PV$, тому пропустіть цей крок.

Крок 5:

$N=2 \times 5=10$платежі

\[FV_{DUE1}=\$ 1,000\left[\dfrac{\left[(1+0.004719 \overline{6})^{\frac{12}{2}}\right]^{10}-1}{(1+0.004719 \overline{6})^{\frac{12}{2}}-1} \times(1+0.004719 \overline{6})^{\frac{12}{2}}\right]=\$ 11,748.47466=FV_1 \nonumber \]

\[\text { Total } FV_{2}=\$ 24,765.17+\$ 38,907.21529=\$ 63,672.39 \nonumber \]

Інструкція калькулятора

Часовий відрізок	Режим	П	В/У	ПВ	PMT	ФВ	П/У	С/У
1	ЛВ	10	5.75	0	-1000	Відповідь: 11,748.47466	2	12
2	$\surd$	52	$\surd$	-11 748,47466	-500	Відповідь: 63 672.385 .29	4	12

На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Коли синові Роберто виповниться 18 років, цільовий фонд матиме залишок у розмірі 63 672,39 доларів.

$clipboard_e3fc621b8f7f70c296f30c64a5c275387.png$

Автори та авторства

Template:ContribBusiMathOlivier

Вправа\(\PageIndex{1}\): Give It Some Thought

Приклад\(\PageIndex{1}\): Future Value of an Investment Account

Приклад\(\PageIndex{2}\): Future Value of a Savings Annuity

Приклад\(\PageIndex{3}\): Saving Up for a Vacation

Вправа\(\PageIndex{2}\): Give It Some Thought

Приклад\(\PageIndex{4}\): Lottery Winnings

Приклад\(\PageIndex{5}\): Saving into a Trust Fund with a Variable Change