11.4: Суми ануїтетних платежів
- Page ID
- 66815
Незалежно від того, чи купуєте ви товари та майно або заощаджуєте до якоїсь майбутньої мети, ви будете мати справу з ануїтетними платежами. Коли ви закінчите коледж і землю, що обіцяє посаду початкового рівня з вашим роботодавцем, багато вимог збираються отримати розміщені на ваш обмежений дохід. Якщо ви ще не володієте власним місцем, можливо, ви отримаєте його. Це означає покупку стартового будинку, за який ви будете робити щомісячні платежі по іпотеці. Щоб заповнити цей будинок, придбання деяких меблів та електроніки може привести вас до цегли, країни сну Канади, Best Buy, або Home Depot. Тоді ви можете бути в шаховому порядку всіх предметів домашнього обслуговування, які вам потрібні. Якщо ви робите багато покупок відразу, ви, ймовірно, скористаєтеся різними планами оплати. Вони пред'являють ще більше вимог до вашого щомісячного доходу. Не забувайте, що деякі колеса вам теж знадобляться. Ви можете як взяти в оренду, так і придбати автомобіль. Чудово, ще один платіж зробити! Нарешті, ви пам'ятаєте, що ваш інструктор з математики навчив вас про важливість початку початку роботи на вашому RRSP, тому ви повинні почати робити ці щомісячні внески найближчим часом.
Чи буде у вас достатній дохід, щоб покрити всі ваші платежі? На відміну від багатьох споживачів, які повинні покладатися на рітейлерів і банків, щоб з'ясувати свої платежі, ваше вивчення аннуїтетних платежів дозволить вам розрахувати суми самостійно.
Підприємства також здійснюють ануїтетні платежі для найрізноманітніших цілей. Будь то економія для майбутніх корпоративних цілей або придбання продуктів і майна, підприємства мають регулярні рахунки, занадто. Маркетологи розробляють плани платежів для своїх споживачів. Фінансові агенти здійснюють інвестиції, що передбачають періодичні платежі. Компанії випускають товарні облігації, які вимагають регулярної виплати відсотків інвесторам. Кадровий персонал доглядає за виплатами працівникам, включаючи внески RRSP та виплати пенсійного плану. Виробничим відділам потрібна дорога техніка, тому вони повинні зберігати плани платежів в рамках операційних бюджетів. Незалежно від вашого вибору професії, як бізнес-менеджер ви зіткнетеся з розрахунками ануїтетних платежів.
Звичайні ануїтети та ануїтети
Розрахувати ануїтетний платіж потрібно в багатьох ситуаціях:
- З'ясування платежів по кредиту або іпотеці
- Визначення планів членства або оплати продукту
- Розрахунок лізингових платежів
- Визначення періодичного платежу, необхідного для досягнення мети заощадження
- Визначення максимального платежу, який інвестиційний ануїтет може витримати протягом певного періоду часу
Типовий графік вирішення суми ануїтетного платежу відображається на наступному малюнку. Відомі всі змінні, крім суми платежу (\(PMT\)). Хоча на малюнку показані всі можливі змінні та їх розташування на часовій шкалі, на кожному кінці часової шкали слід зазначити наступне:

- Якщо\(PV_{DUE}\) або\(PV_{ORD}\) відомий зліва, то\(FV\) це єдина змінна, яка може з'явитися праворуч. \(FV_{DUE}\),\(FV_{ORD}\), і\(PV\) є змінними, які не відображатимуться на часовій шкалі.
- Якщо\(FV_{DUE}\) або\(FV_{ORD}\) відомо праворуч, то\(PV\) це єдина змінна, яка може з'явитися зліва. \(PV_{DUE}\),\(PV_{ORD}\), і\(FV\) є змінними, які не відображатимуться на часовій шкалі.
Формула
Нагадаємо, що сума ануїтетного платежу\(PMT\), є однією зі змінних у Формулі 11.2, Формулі 11.3, Формулі 11.4 та Формулі 11.5. Потім обчислення цієї суми вимагає підставити відомі змінні та змінити формулу для PMT. Найскладнішою частиною цього процесу є з'ясування, яку з чотирьох формул використовувати. Ваш вибір залежить від двох факторів, узагальнених у цій таблиці та обговорюваних згодом.
| Формула для використання | Терміни виплати ануїтету | Значення ануїтету відоме |
|---|---|---|
| 11.2 | Кінець | \(FV_{ORD}\) |
| 11.4 | Кінець | \(PV_{ORD}\) |
| 11.3 | Початок | \(FV_{DUE}\) |
| 11.5 | Початок | \(PV_{DUE}\) |
- Чи потрібно проводити ануїтетні платежі на початку або в кінці інтервалу платежів? Іншими словами, чи є у вас ануїтет або звичайний ануїтет?
- Чи знаєте ви суму, з якої починається або закінчується ануїтет? Іншими словами, чи знаєте ви поточну вартість або майбутню вартість ануїтету?
Як це працює
Виконайте наступні дії, щоб вирішити будь-яку суму ануїтетного платежу:
- Крок 1: Визначте тип ануїтету. Намалюйте часову шкалу, щоб візуалізувати питання.
- Крок 2: Визначте змінні, які ви знаєте, включаючи\(IY, CY, PY\), і роки. Ви також повинні визначити значення для одного з\(PV_{ORD}\)\(PV_{DUE}\),\(FV_{ORD}\), або\(FV_{DUE}\). Ви можете або не мати значення для\(FV\) або\(PV\).
- Крок 3: Використовуйте формулу 9.1 для розрахунку\(i\).
- Крок 4: Якщо один платіж\(PV\) або\(FV\) відомий, перемістіть його на інший кінець часового відрізка за допомогою Формули 9.3. Щоб визначити\(N\), застосуйте Формулу 9.2, оскільки це стосується єдиного платежу, а не ануїтету. Коли ви переміщуєте суму на ту ж фокусну дату, що і теперішня або майбутня вартість ануїтету, або додайте це число до вартості ануїтету або відніміть його, як вимагає ситуація. Приклад\(\PageIndex{3}\) далі в цьому розділі проілюструє цю практику.
- Крок 5: Використовуйте формулу 11.1 для розрахунку\(N\). Застосуйте правильну формулу ануїтетного платежу, яка відповідає вашому типу ануїтету та відомої теперішньої або майбутньої вартості. Виберіть формулу 11.2, Формула 11.3, Формула 11.4 або Формула 11.5, а потім перевпорядкуйте суму ануїтетного платежу,\(PMT\). Якщо ви виконали крок 4 вище, обов'язково використовуйте скориговану майбутню або теперішню вартість вашої ануїтету у формулі.
Важливі зауваження
При розрахунку платежів по кредиту нагадайте, що останній платіж трохи відрізняється від всіх інших платежів. Глава 13 досліджує, як точно розрахувати останній платіж. Для цілей цього розділу розглядайте останній платіж, як і будь-який інший платіж, і припускайте, що він дорівнює всім іншим платежам, коли ви робите будь-яку заяву про суми або суми платежу по кредиту.
Речі, на які слід остерігатися
Чи варто рости або зменшити баланс? Дайте деяку думку про відносини між поточною вартістю, ануїтетними платежами та майбутньою вартістю.
- Якщо хтось сприяє інвестиції, майбутня вартість ануїтету повинна бути більшою, ніж загальна сума всіх ануїтетних платежів.
- Якщо хтось отримує від інвестиції або здійснює боргові платежі, загальна сума всіх ануїтетних платежів повинна перевищувати поточну вартість.
- Інвестор робить $1000 щорічних внесків на свій рахунок протягом п'яти років. У цій задачі, чи повинна майбутня вартість бути більше, менше або дорівнює $5,000?
- Боржник повинен робити 1000 доларів щорічних платежів по її кредиту протягом п'яти років, щоб погасити свій борг. У цій задачі, чи повинна теперішня вартість бути більше, менше або дорівнює $5,000?
- Пенсійний фонд може зробити п'ять щорічних виплат в розмірі 1000 доларів до гасіння. У цій задачі, чи повинна теперішня вартість бути більше, менше або дорівнює $5,000?
- Відповідь
-
- Майбутня вартість становитиме більше $5,000. На виплати заробляють відсотки.
- Нинішня вартість становитиме менше $5,000. Платежі представляють основну суму та відсотки разом.
- Нинішня вартість становитиме менше $5,000. Принципал заробляє відсотки при виплаті.
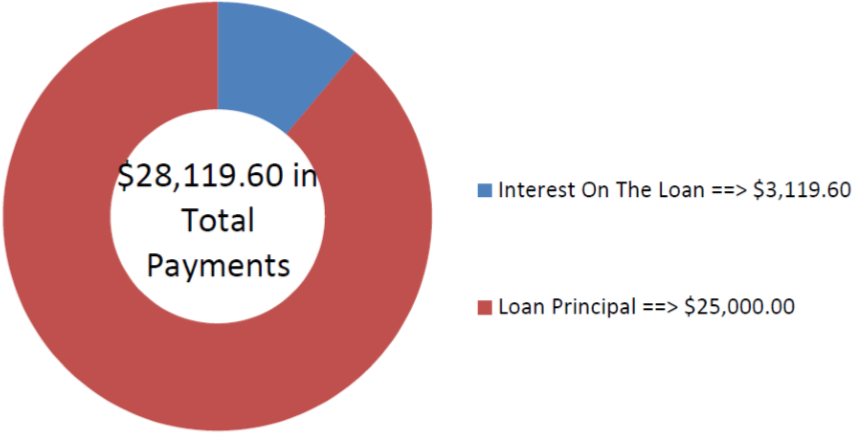
Morgan хоче консолідувати багато менших боргів в єдиний трирічний кредит на $25 000. Якщо по кредиту нараховуються відсотки під 7,8%, що складаються щомісяця, то яка сума її платежу в кінці кожного місяця?
Рішення
Крок 1:
Виплати здійснюються в кінці інтервалів платежів, а період складання та інтервали виплат однакові. Тому це звичайна проста ануїтет. Розрахувати щомісячну суму її кредитного платежу, або\(PMT\).
Що ви вже знаєте
Крок 1 (продовження):
Хронологія кредиту відображається нижче.

Крок 2:
\(PV_{ORD}\)= $25 000,\(IY\) = 7,8%,\(CY\) = 12,\(PY\) = 12, років = 3,\(FV\) = 0$
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Оскільки\(FV\) = $0, пропустіть цей крок.
Крок 5:
Застосуйте Формулу 11.1 і Формулу 11.4, переставляючи для\(PMT\).
Виконувати
Крок 3:
\[i=7.8 \% \div 12=0.65 \% \nonumber \]
Крок 5:
\(N=12 \times 3=36\)платежі
\[\$ 25,000=PMT\left[\dfrac{1-\left[\frac{1}{(1+0.0065)^{\frac{12}{12}}}\right]^{36}}{(1+0.0065)^{\frac{12}{12}}-1}\right] \nonumber \]
\[PMT=\dfrac{\$ 25,000}{32.005957}=\$ 781.10 \nonumber \]
Інструкції з калькулятора
| П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|
| 36 | 7.8 | 25000 | Відповідь: -781.104587 | 0 | 12 | 12 |
На малюнку видно, скільки основного боргу і відсотків складають виплати. Щоб погасити її консолідований кредит, виплати Morgan на кінець місяця протягом наступних трьох років складуть $781,10.
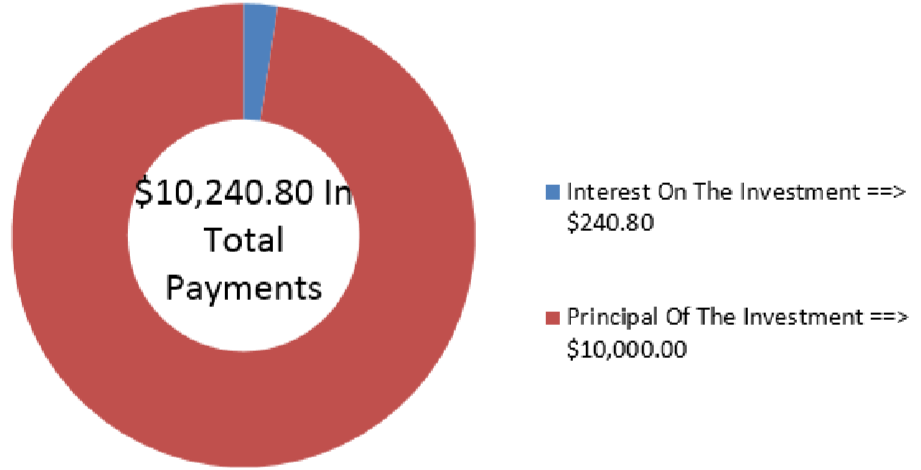
Франко розмістив $10,000 в інвестиційний фонд з метою отримання рівних сум на початку кожного місяця протягом наступного року, поки він рюкзаки по всій Європі. Якщо інвестиційний фонд може заробляти 5,25% в сукупності щоквартально, скільки грошей Франко може розраховувати отримувати щомісяця?
Рішення
Крок 1:
Платежі знаходяться на початку інтервалів платежів, а період складання та інтервали платежів різні. Тому це загальна рента за рахунок. Розрахувати щомісячну суму, яку він може отримати, або\(PMT\).
Що ви вже знаєте
Крок 1 (продовження):
Графік для відпускних грошей відображається нижче.

Крок 2:
\(PV_{DUE}\)= $10,000,\(IY\) = 5,25%,\(CY\) = 4,\(PY\) = 12, роки=1,\(FV\) = 0$
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Оскільки\(FV\) = $0, пропустіть цей крок.
Крок 5:
Застосуйте Формулу 11.1 і Формулу 11.3, переставляючи для\(PMT\).
Виконувати
Крок 3:
\[i=5.25 \% \div 4=1.3125 \% \nonumber \]
Крок 5:
\(N=12 \times 1=12\)платежі
\[\$ 10,000=PMT\left[\dfrac{1-\left[\frac{1}{(1+0.013125)^{\frac{4}{12}}}\right]^{12}}{(1+0.013125)^{\frac{4}{12}}-1}\right] \times(1+0.013125)^{\frac{4}{12}} \nonumber \]
\[PMT=\dfrac{\$ 10,000}{11.717849}=\$ 853.40 \nonumber \]
Інструкції з калькулятора
| Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| ЛВ | 12 | 5.25 | -10000 | Відповідь: 853.398928 | 0 | 12 | 4 |
На малюнку видно, скільки основного боргу і відсотків складають виплати. Під час рюкзака по всій Європі, Франко буде мати його ануїтет платити йому $853.40 на початку кожного місяця.
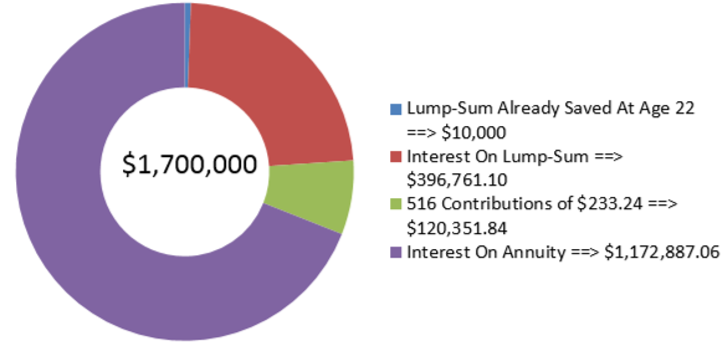
Фінансовий радник Кінгслі визначив, що коли він досягне 65 років, йому знадобиться 1,7 мільйона доларів у своєму RRSP для фінансування його виходу на пенсію. Кінгслі в даний час 22 роки і вже заощадив 10 000 доларів. Його радник вважає, що його RRSP становитиме в середньому 9% щорічно протягом багатьох років. Щоб досягти своєї мети RRSP, скільки Кінгслі потрібно інвестувати щомісяця, починаючи з сьогоднішнього дня?
Рішення
Крок 1:
Виплати здійснюються на початку інтервалів платежів, а період складання та інтервали виплат різні. Тому це загальна рента за рахунок. Розрахуйте щомісячну суму, яку Кінгслі потрібно внести, або PMT.
Що ви вже знаєте
Крок 1 (продовження):
Хронологія внесків RRSP Кінгслі відображається нижче.

Крок 2:
\(PV\)= $10,000,\(FV_{DUE}\) = $1,700 000,\(IY\) = 9%,\(CY\) = 1,\(PY\) = 12, років = 43
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Вам потрібно перенести теперішнє значення на 65 років Кінгслі, ту ж дату, що і\(FV_{DUE}\). Застосовуйте формулу 9.2 та формулу 9.3. The\(FV\) гроші, які ануїтет не повинен економити, тому ви віднімаєте їх,\(FV_{DUE}\) щоб прийти до суми, яку повинен генерувати ануїтет.
Крок 5:
Застосовуємо Формулу 11.1 і Формулу 11.3, переставляючи для\(PMT\), використовуючи скориговані\(FV_{DUE}\).
Крок 3:
\[i=9 \% \div 1=9 \% \nonumber \]
Крок 4:
\(N=1 \times 43=43\)сполуки
\[FV=\$ 10,000(1+0.09)^{43}=\$ 406,761.0984 \nonumber \]
\[\text { New } FV_{DUE}=\$ 1,700,000-\$ 406,761.0984=\$ 1,293,238.902 \nonumber \]
Крок 5:
\(N=12 \times 43=516\)платежі
\[\$ 1,293,238.902=PMT\left[\dfrac{\left((1+0.09)^{\frac{1}{12}}\right]^{516}-1}{(1+0.09)^{\frac{1}{12}}-1}\right) \times(1+0.09)^{\frac{1}{12}} \nonumber \]
\[PMT=\dfrac{\$ 1,293,238.902}{5,544.647665}=\$ 233.24 \nonumber \]
Інструкції з калькулятора
| Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| ЛВ | 516 | 9 | -10000 | Відповідь: -233.240952 | 1700000 | 12 | 1 |
На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Щоб досягти своїх пенсійних цілей, Кінгслі потрібно інвестувати 233,24 долара на початку кожного місяця протягом наступних 43 років. Роблячи це, він досягне залишку на своєму рахунку в 1,7 мільйона доларів у віці 65 років. (Примітка: Подібно до кредитних платежів, останній платіж насправді повинен бути трохи більшою сумою, оскільки ануїтетний платіж був округлений у меншу сторону. Однак останній платіж в цей час розглядається однаково для цілей всіх розрахунків.)
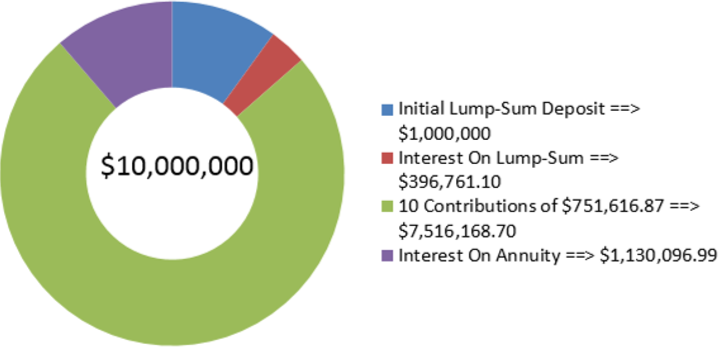
Виробничий відділ щойно повідомив фінансовий відділ, що через п'ять років роботизовані системи на виробничій лінії потрібно буде замінити. Орієнтовна вартість заміни становить $10 млн. Щоб підготуватися до цієї покупки, фінансовий відділ негайно вносить $1,000,000 в ощадний ануїтет, який заробляє 6,15%, складений півроку, і він планує робити піврічні внески, починаючи з шести місяців. Наскільки великими повинні бути ці внески?
Рішення
Крок 1:
Виплати здійснюються в кінці інтервалів платежів, а період складання та інтервали виплат однакові. Тому це звичайна проста ануїтет. Розрахуйте щомісячну суму, яку фінансовий відділ повинен внести, або\(PMT\).
Що ви вже знаєте
Крок 1 (продовження):
Графік роботи фонду машин відображається нижче.

Крок 2:
\(PV\)= $1,000,000,\(FV_{ORD}\) = $10 000 000,\(IY\) = 6.15%,\(CY\) = 2,\(PY\) = 2, років = 5
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Приведена вартість повинна бути перенесена на п'ятирічну дату, ту ж дату, що і\(FV_{ORD}\). Застосувати Формулу 9.2 та Формулу 9.3.\(FV\) Це гроші, які ануїтет не повинен економити, тому він віднімається,\(FV_{ORD}\) щоб отримати суму, яку повинен генерувати ануїтет.
Крок 5:
Застосовуємо Формулу 11.1 і Формулу 11.2, переставляючи для\(PMT\), використовуючи скориговані\(FV_{ORD}\).
Крок 3:
\[i=6.15 \% \div 2=3.075 \% \nonumber \]
Крок 4:
\(N=2 \times 5=10 \)сполуки
\[FV=\$ 1,000,000(1+0.03075)^{10}=\$ 1,353,734.306 \nonumber \]
\[\text { New } FV_{ORD}=\$ 10,000,000-\$ 1,353,734.306=\$ 8,646,265.694 \nonumber \]
Крок 5:
\(N=2 \times 5=10\)платежі
\[\$ 8,646,265.694=PMT\left[\dfrac{\left[(1+0.03075)^{\frac{2}{2}}\right]^{10}-1}{(1+0.03075)^{\frac{2}{2}}-1}\right] \nonumber \]
\[PMT=\dfrac{\$ 8,646,265.694}{11.503554}=\$ 751,616.87 \nonumber \]
Інструкції з калькулятора
| П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|
| 10 | 6.15 | -1000000 | Відповідь: -751,616.8656 | 10000000 | 2 | 2 |
На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Щоб мати адекватне фінансування для заміни машин виробничої лінії через п'ять років, фінансовий відділ повинен вносити до фонду 751,616,87 доларів кожні шість місяців. (Примітка: Подібно до кредитних платежів, останній платіж насправді повинен бути трохи меншою сумою, оскільки ануїтетний платіж був округлений у більшу сторону. Однак останній платіж в цей час розглядається однаково для цілей всіх розрахунків.)