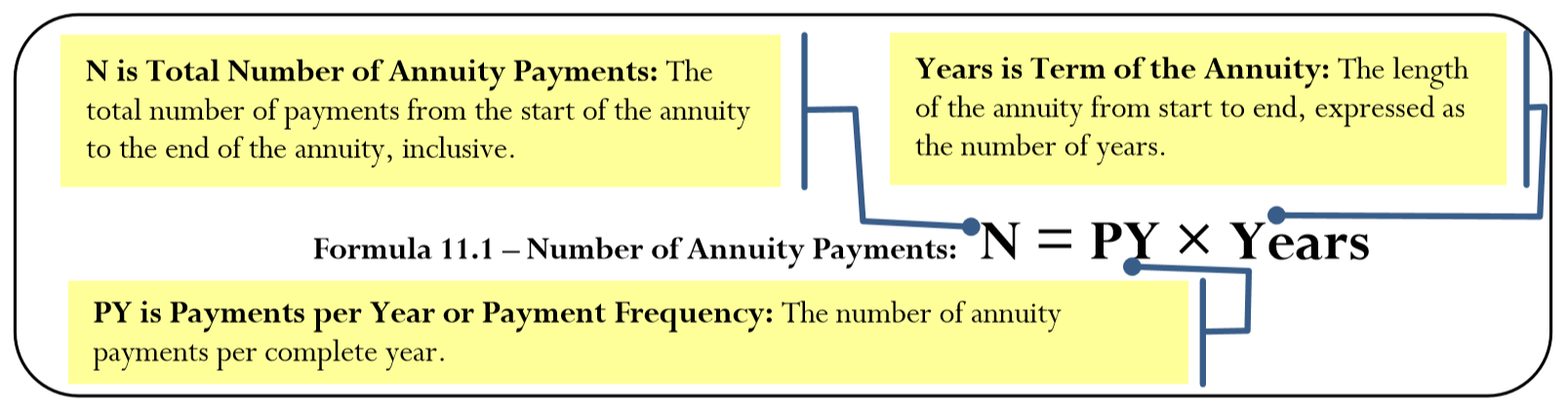
11.1: Основи ануїтетів

Last updated
Save as PDF

Page ID: 66805

Jean-Paul Olivier
Red River College of Applied Arts, Science, & Technology

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Неможливо точно розрахувати платежі, поки ви не розпізнаєте кілька ключових характеристик, проілюстрованих у вступі до розділу:

Всі приклади вимагали виплати в тій же сумі на регулярній основі, наприклад, $872.41 щомісяця для вашої іпотеки.
Терміни проведення виплат варіювалися. Лізинг автомобіля вимагав першої оплати авансом (на початку місяця), тоді як іпотека та придбання матраца мали перший платіж через місяць після покупки (наприкінці місяця).
Частота виплат і частота процентної ставки змінювалися. Іпотека мала щомісячні платежі з відсотками, що нараховувалися півроку, тоді як лізинг автомобіля мав щомісячні платежі та щомісячні відсотки.

На відміну від одиночних платежів (розглянутих у розділі 9), для яких існує лише одна формула, ви вирішуєте серію платежів, вибираючи відповідну формулу з чотирьох можливостей, визначених фінансовими характеристиками платежів. Цей розділ визначає характеристики чотирьох різних типів платіжних серій, а потім контрастує їх з главою 9 та главою 10 розрахунків єдиного платежу. Цей розділ також розробляє нову спрощену структуру часових шкал, яка допоможе вам візуалізувати серію платежів.

Що таке ануїтети?

Аннуїтет - це безперервний потік рівних періодичних платежів від однієї сторони до іншої протягом певного періоду часу для виконання фінансового зобов'язання. Аннуїтетний платіж - це доларова сума рівного періодичного платежу в умовах ануїтету. На малюнку нижче показана шестимісячна ануїтет з щомісячними платежами. Зверніть увагу, що платежі є безперервними, рівними, періодичними і відбуваються протягом фіксованого періоду часу. Якщо будь-яка з цих чотирьох характеристик не задовольняється, то фінансова операція не відповідає визначенню сингулярного ануїтету і вимагає вирішення інших методів та формул.

$clipboard_e554f8d5c481e045024b7d25b08ae4e8a.png$

Наведені нижче приклади ілюструють чотири терміни, які виглядають подібно до наведеного вище, але з порушенням однієї з характеристик ануїтету. Це означає, що жодне з перерахованих нижче в повному обсязі не вважається ануїтетом:

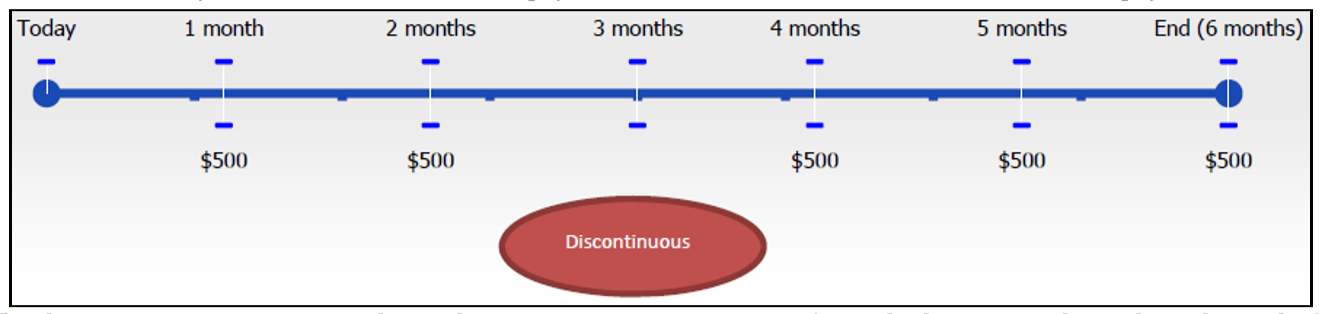
Безперервний. Ануїтетні виплати проходять без перерви або перерв від початку до кінця терміну ануїтету. На малюнку вище немає перерв в ануїтет, оскільки кожен місяць має ануїтетний платіж. Ця наступна цифра не є ануїтетом, оскільки відсутність платежу в третьому місяці робить серію платежів переривчастими.

$clipboard_eaf71a2a3b3063170b5eefdf74f06a7e1.png$

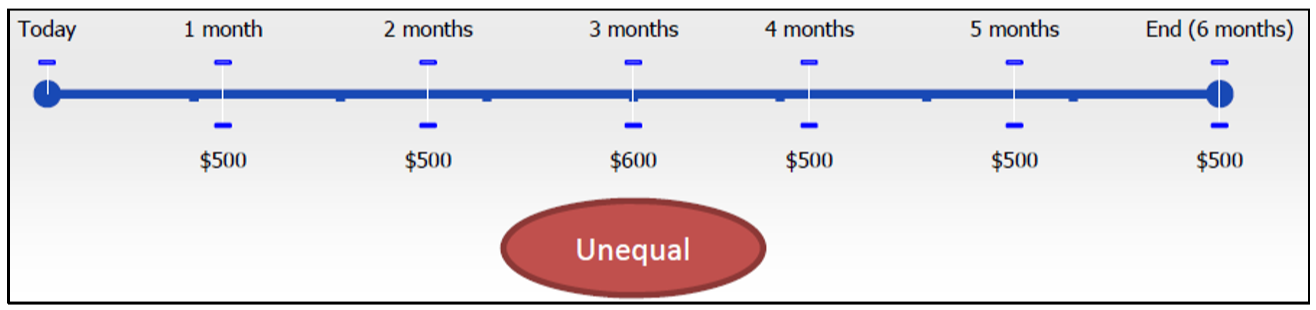
Рівні. Ануїтетні платежі повинні бути в однаковій сумі кожен раз від початку до кінця терміну ануїтету. У первісному показнику кожен щомісячний ануїтет становить 500 доларів. Зверніть увагу, що в цій наступній цифрі сума платежу варіюється і включає значення як $500, так і $600.

$clipboard_ea4de913d6be6d3922284947a8b3c38da.png$

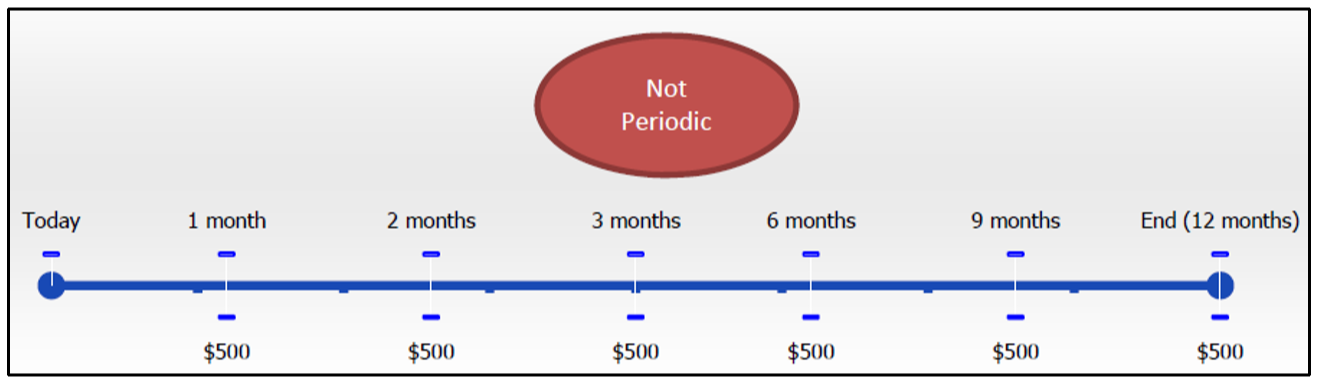
Періодичні. Кількість часу між кожним безперервним і рівним ануїтетним платежем відомий як інтервал оплати. Отже, щомісячний інтервал платежів означає, що платежі мають один місяць між ними, тоді як піврічний інтервал платежів означає, що платежі мають шість місяців між ними. Ануїтетні платежі завжди повинні мати однаковий інтервал виплат від початку до кінця терміну ануїтету. У вихідній цифрі є рівно один місяць між кожним рівним і повторним платежем в ануїтет. Зверніть увагу, що в цій наступній цифрі платежі, хоча і рівні та безперервні, не відбуваються з однаковою кількістю часу між кожним. Фактично перші три платежі здійснюються щомісяця, тоді як останні три платежі здійснюються щоквартально. (Ви можете помітити, що якщо перші три платежі розглядаються окремо від останніх трьох платежів, то кожна окрема угруповання являє собою ануїтет і тому існує два окремих ануїтетів. Однак в цілому це не ануїтет.)

$clipboard_e9f85edae5cabfc59103ffc8fd03f88ef.png$

Зазначений період часу. Ануїтетні платежі повинні відбуватися протягом визначеного періоду часу, який має вказаний початок і вказаний кінець. Тимчасові рамки ануїтету можуть бути (1) відомі з визначеною датою початку та визначеною датою закінчення, наприклад, ануїтет, проілюстрований у вихідній цифрі, яка триває протягом шести періодів; (2) відомий, але незавершений, наприклад, початок сьогодні і триває назавжди в майбутнє (отже, нескінченний період часу); або (3) невідомий, але має чітку точку припинення, наприклад, щомісячні пенсійні виплати, які починаються, коли ви виходите на пенсію, і закінчуються, коли ви помираєте - дата, яка, очевидно, не відома заздалегідь. На наступному малюнку ануїтет не має визначеної дати закінчення, не продовжується в майбутньому, і жодна чітка точка припинення не може бути ідентифікована.

$clipboard_ee238a31868aa3623ab266b02028f4666.png$

Підсумовуючи, перша цифра - це ануїтет, який дотримується всіх чотирьох характеристик і може бути вирішений за допомогою ануїтетної формули. Наступні чотири цифри не є ануїтетами і потребують інших фінансових прийомів або формул для виконання будь-яких необхідних розрахунків.

Види ануїтетів

Існує чотири види ануїтетів, які засновані на поєднанні двох ключових характеристик: термінів виплат і періодичності. Давайте спочатку вивчимо ці характеристики, після чого обговоримо різні типи ануїтету.

Терміни проведення платежів. Приклад найкраще ілюструє цю характеристику. Припустимо, що ви берете кредит сьогодні з щомісячними платежами. Якщо ви повинні були зробити свій перший ануїтетний платіж в день, коли ви берете кредит, сума основного боргу буде негайно зменшена, і ви б накопичити меншу суму відсотків протягом першого місяця. Це називається здійсненням ануїтетного платежу на початку інтервалу платежів, і цей платіж відомий як належний. Однак, якщо проходить місяць, перш ніж ви зробите свій перший щомісячний платіж по кредиту, ваш початковий основний капітал накопичує більше відсотків, ніж якби основна сума вже була зменшена. Це називається здійсненням платежу в кінці інтервалу оплати, і цей платіж відомий як звичайний, оскільки це найпоширеніша форма ануїтетного платежу. Залежно від того, коли ви здійснюєте платіж, виникають різні суми основного боргу та відсотки.
Частота. Частота ануїтету відноситься до порівняння між частотою виплат і частотою складання. Частота виплат - це кількість ануїтетних платежів, які відбуватимуться протягом усього року. Нагадаємо з глави 9, що частота компаундування - це кількість сполук за повний рік. Якщо частота виплат збігається з частотою складання, це називається простим ануїтетом. Коли відсотки нараховуються на рахунок щомісяця, а платежі також здійснюються щомісяця, ви визначаєте основну суму та відсотки за спрощеними формулами. Однак, якщо частота виплат і частота складання різні, це називається загальним ануїтетом. Якщо, наприклад, ви робите платежі щомісяця, а відсотки посилюються піврічно, вам доведеться використовувати більш складні формули для визначення основного боргу та відсотків, оскільки виплата основного боргу та нарахування відсотків не відбувається одночасно.

Покладання цих двох характеристик разом у їх чотирьох комбінаціях створює чотири типи ануїтетів. Кожен графік у цих цифрах передбачає транзакцію, яка передбачає шість піврічних платежів протягом трирічного періоду часу.

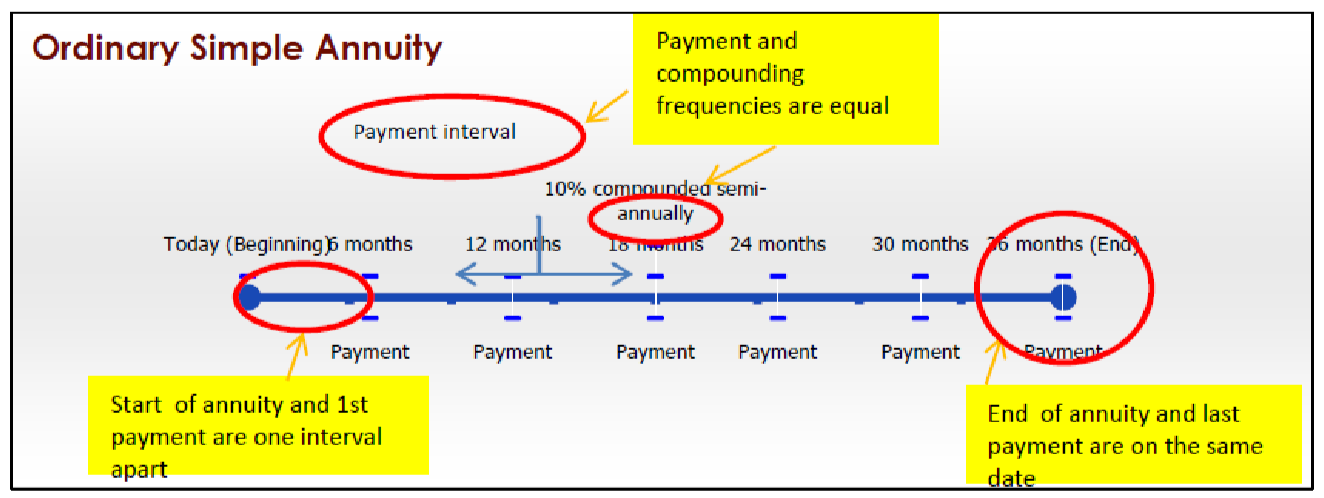
$clipboard_ed515063a3f2494da95647671f5e35dbe.png$

Звичайний простий ануїтет

Звичайна проста рента має такі характеристики:

Платежі здійснюються в кінці інтервалів платежів, а частоти оплати і складання рівні.
Перший платіж відбувається через один проміжок після початку ануїтету.
Останній платіж відбувається в ту ж дату закінчення ануїтету.

Наприклад, більшість автокредитів - це звичайні прості ануїтети, де платежі здійснюються щомісяця, а процентні ставки збільшуються щомісяця. Так само автокредити не вимагають першого щомісячного платежу до кінця першого місяця.

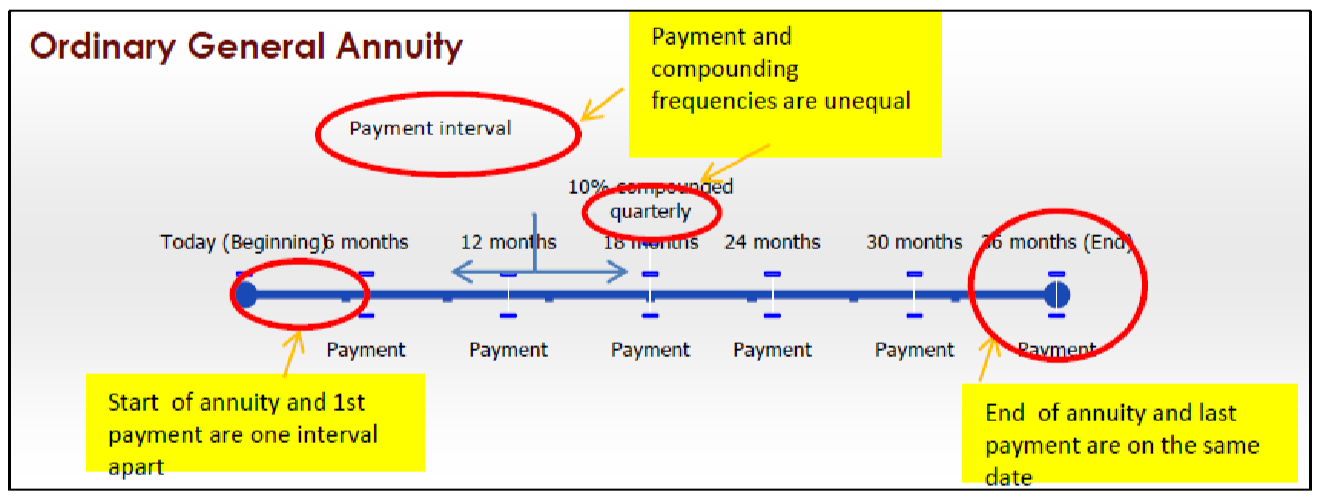
$clipboard_eecdddc770fa7a30e8eb165d3c7e69a7d.png$

Звичайний загальний ануїтет

Звичайна загальна рента має такі характеристики:

Платежі здійснюються в кінці інтервалів платежів, а частоти оплати і складання нерівні.
Перший платіж відбувається через один проміжок після початку ануїтету.
Останній платіж відбувається в ту ж дату закінчення ануїтету.

Наприклад, більшість іпотечних кредитів - це звичайні загальні ануїтети, де виплати здійснюються щомісяця, а процентні ставки збільшуються піврічних. Як і у випадку з автокредитами, ваш перший щомісячний платіж не потрібно, поки не пройде один місяць.

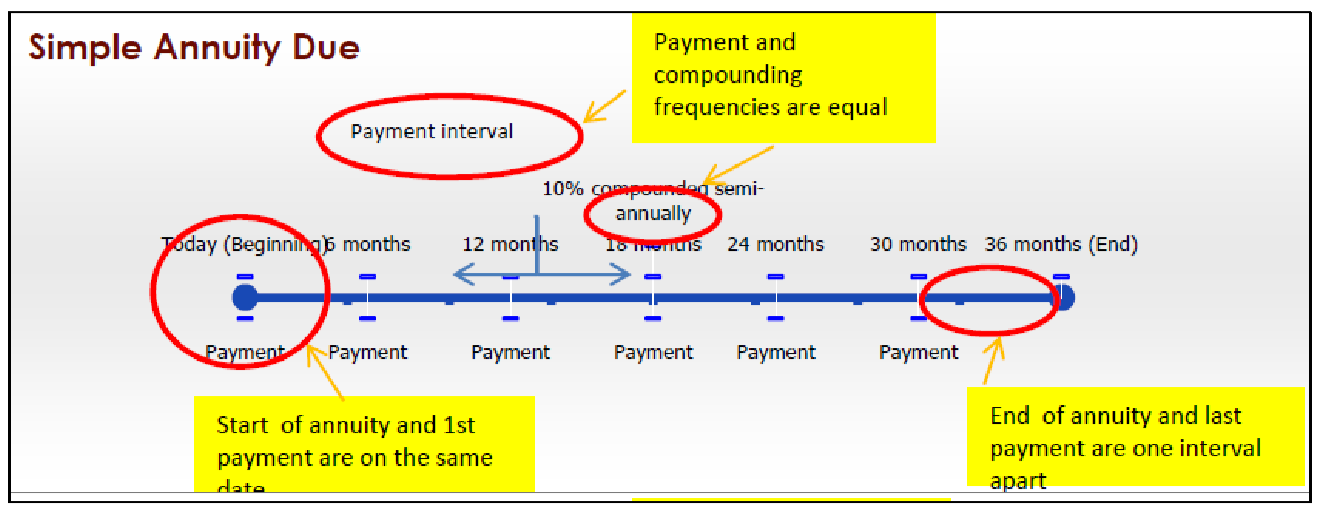
$clipboard_e4261d6176a026de70ada501d33c26522.png$

Простий ануїтет через

Проста рента за рахунок має такі характеристики:

Платежі здійснюються на початку інтервалів платежів, а частоти оплати і складання рівні.
Перший платіж відбувається в ту ж дату, що і початок ануїтету.
Останній платіж відбувається за один платіжний інтервал до закінчення ануїтету.

Наприклад, більшість оренди автомобілів - це прості ануїтети за рахунок, де виплати здійснюються щомісяця, а процентні ставки збільшуються щомісяця. Однак день, коли ви підписуєте договір оренди, коли ви повинні зробити свій перший щомісячний платіж.

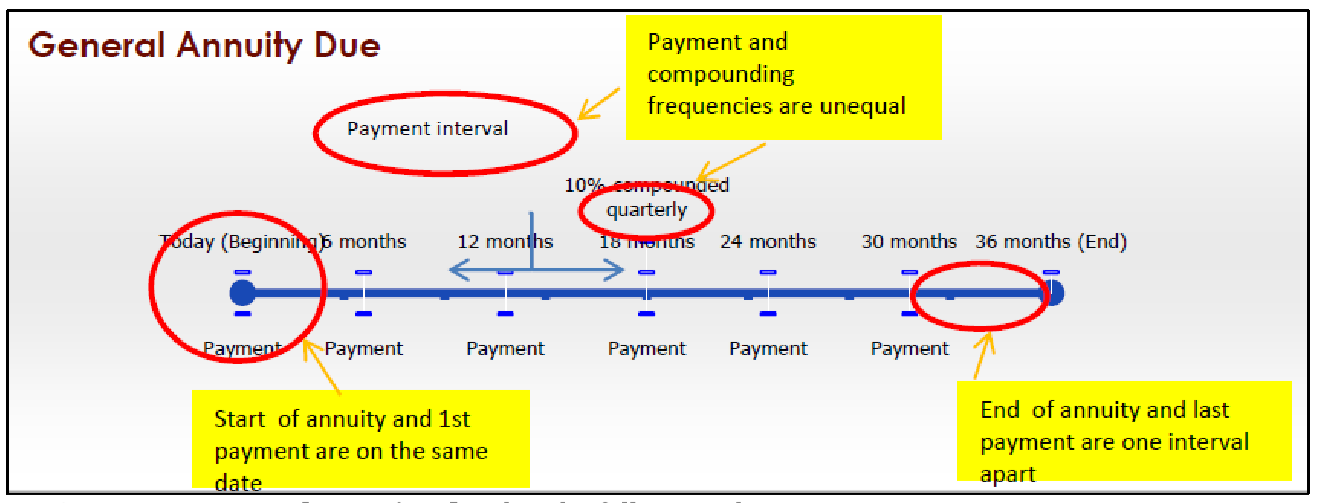
$clipboard_e26d04f5a2f646857c41be019daed72f3.png$

Загальний ануїтет Due.

Загальна рента за рахунок має такі характеристики:

Платежі здійснюються на початку інтервалів платежів, а частоти оплати і складання нерівні.
Перший платіж відбувається в ту ж дату, що і початок ануїтету.
Останній платіж відбувається за один платіжний інтервал до закінчення ануїтету.

Наприклад, багато інвестицій, як ваш RRSP, є загальними ануїтетами, які належать, коли платежі (внески) зазвичай здійснюються щомісяця, але відсотки складаються іншим способом, наприклад, щорічно. Крім того, коли більшість людей починають RRSP, вони платять у нього в день, коли вони його налаштували, а це означає, що їх RRSP починається з першого внесеного платежу.

У таблиці нижче узагальнено чотири типи ануїтетів та їх характеристики для зручності ознайомлення.

Тип ануїтету	Терміни проведення платежів у платіжному інтервалі	Частота платежів та періодичність складання	Початок ануїтету та першого платежу тієї ж дати?	Кінець ануїтету та останній платіж тієї ж дати?
Звичайний простий ануїтет	Кінець	Рівні	Ні, перший платіж через один інтервал	Так
Звичайний загальний ануїтет	Кінець	Нерівні	Ні, перший платіж через один інтервал	Так
Простий ануїтет через	Початок	Рівні	Так	Ні, останній платіж на один інтервал раніше
Загальний ануїтет	Початок	Нерівні	Так	Ні, останній платіж на один інтервал раніше

Шляхи до успіху

Одним з найбільш складних аспектів ануїтетів є визнання того, чи ануїтет ви працюєте з є звичайним або належним. Ця відмінність відіграє вирішальну роль у виборі формули пізніше в цьому розділі. Щоб допомогти вам розпізнати різницю, наведена нижче таблиця узагальнює деякі ключові слова разом із загальними програмами, в яких може з'явитися ануїтет.

Тип	Ключові слова або фрази	Загальні програми
Звичайний	-... виплати в кінці... -... виплати не починаються сьогодні... -... виплати пізніше... -... перший платіж наступний інтервал...	- банківські кредити будь-якого типу - іпотека - облігації - Канада Пенсійний план (CPP)
Через	-... виплати на початку... -... виплати починаються сьогодні... -... платежі заздалегідь... -... перший платіж сьогодні... -... виплати починаються зараз...	- будь-який вид оренди - будь-який вид оренди - RRSP (зазвичай) - членські внески - страхування

Ануїтети проти єдиних платежів

Щоб перейти від разових платежів у розділі 9 до ануїтетів в цьому розділі, вам потрібно зробити кілька адаптацій:

Сума ануїтетного платежу (PMT). Ця змінна не використовувалася ні в одній з формул, представлених у Главі 9 або Главі 10, хоча вона була коротко введена при розділі 9.2 при демонстрації функцій калькулятора. Зверніть увагу, що в попередніх двох розділах ця змінна була встановлена на нуль для кожного питання, оскільки кожен платіж не був частиною ануїтету. Розрахунки ануїтету вимагають прив'язати значення до цієї змінної в формулах і при використанні технології, такі як калькулятор BAII+.
Періодичність платежів або платежі на рік (PY). Для одиночних платежів ця змінна не відображалася ні в одній з формул попередніх двох розділів. Він також був введений в розділі 9.2 як кнопка калькулятора з вимогою, щоб вона автоматично встановлювалася як нульова змінна, що відповідає частоті компаундирования (CY). При роботі з ануїтетами фактична вартість для$PY$ визначається періодичністю виплат. Для простих ануїтетів$PY$ залишається таким же$CY$, як, тоді як змінні відрізняються для загальних ануїтетів.
Договір про рух грошових коштів на калькуляторі. Тепер стає критичним забезпечити належне застосування конвенції про знак грошового потоку на калькуляторі - невиконання цього призведе до неправильної відповіді. Наприклад, якщо ви позичаєте гроші, а потім робите на них ануїтетні платежі, ви вводите поточне значення ($PV$) як позитивне (ви отримали гроші), а ви вводите ануїтетні платежі як негативи (ви заплатили гроші банку). Це призводить до того, що майбутні залишки стають меншими, і ви зобов'язані менше грошей. Якщо ви ненавмисно вводите ануїтетний платіж як позитивне число, це означатиме, що ви позичаєте більше грошей у банку, щоб ваш майбутній баланс збільшився, і ви заборгували більше грошей. Ці дві відповіді дуже різні!
Визначення та обчислення N. Коли ви працювали з разовими платежами,$N$ було визначено загальну кількість з'єднань протягом усього терміну фінансової операції. Коли ви працюєте з ануїтетами,$N$ визначається як загальна кількість виплат протягом усього терміну ануїтету. Ви розраховуєте його за допомогою Формули 11.1.

Формула

$clipboard_e3982a10b50df004be3651e1a0b8b9776.png$

Формула 11.1

Як це працює

За дворічним кредитом з щомісячними платежами і піврічним складанням періодичність виплат щомісяця, або 12 разів на рік. З терміном два роки, що робить N = 2 × 12 = 24 платежі. Зверніть увагу, що розрахунок N для ануїтету не передбачає частоту складання.

Адаптація термінів для включення ануїтетів

Питання ануїтету можуть включати багато платежів. Наприклад, у типовій 25-річній іпотеці з щомісячними платежами, це було б 25 × 12 = 300 платежів загалом. Як би ви намалювали часову шкалу для них? Зрозуміло, що залучати 300 платежів було б недоцільно.

Хороший графік ануїтету повинен ілюструвати поточну вартість ($PV$), майбутню вартість ($FV$), кількість ануїтетних платежів ($N$), номінальну процентну ставку ($IY$), частоту складання ($CY$), ануїтетний платіж ($PMT$) та частоту виплат ($PY$). Однією з цих змінних буде невідома.

Крім того, хороший графік вимагає чіткого розмежування між звичайними ануїтетами та ануїтетами за рахунок. END використовується для представлення звичайних ануїтетів, так як виплати відбуваються в кінці інтервалу платежів. Аналогічно, BGN використовується для представлення належних ануїтетів, оскільки платежі відбуваються на початку інтервалу платежів. На малюнку нижче показано адаптований формат часової шкали ануїтету.

$clipboard_e16e2147badf8e54f249103053c617a54.png$

S іноді змінна буде змінюватися частково через період ануїтету, і в цьому випадку терміни повинні бути розбиті на два або більше сегментів. Коли ви використовуєте цю структуру, у будь-якому часовому сегменті$PMT$ ануїтетний платіж інтерпретується як однакова сума на одному інтервалі платежів безперервно протягом усього сегмента. Кількість ануїтетних платежів безпосередньо$N$ не відображається на часовій шкалі, оскільки це результат формули. Однак дві його складові (Years and PY) намальовані на часовій шкалі.

Як це працює

Іпотека використовується для ілюстрації цього нового формату. Наразі зосередьтеся строго на змінних і на тому, як їх проілюструвати на часовій шкалі. Поки не орієнтуйтеся на будь-які розрахунки по іпотеці.

Відповідно до введення глави, ви придбали будинок $150,000 ($PV$) з 25-річною іпотекою (років). Ставка по іпотеці становить 5% ($IY$), що складається півроку ($CY$= 2), а щомісячні платежі ($PY$= 12) складають 872,41$ ($PMT$).
Через 25 років ви будете володіти своїм будинком і, отже, не залишиться балансу. Це встановлює майбутнє значення $0 ($FV$).
Іпотека носить звичайний характер, тобто виплати відбуваються в кінці інтервалів платежів (END). На малюнку нижче розміщують всі ці іпотечні елементи в новому форматі часової шкали. Після того, як ви намалювали часову шкалу, ви можете визначити наступне:

$clipboard_e91ba49fb9126eb6eda5eb3ae7f588d73.png$

Кількість платежів ($N$), яку ви розраховуєте за формулою 11.1. Оскільки обидва$PY$ і роки відомі, у вас є$N$ = 25 × 12 = 300.
Чи є ануїтет простий або загальний, що залежить від наведеної$PY$ нижче часової шкали та$CY$ вище часової шкали. Якщо вони збігаються, ануїтет простий; якщо вони відрізняються, як у цьому прикладі, це загальне.

Речі, на які слід остерігатися

Слово «оплата» часто бентежить людей, оскільки має два тлумачення. Це може означати або «єдиний платіж», наприклад, у розділі 9, або «ануїтетний платіж», що мається на увазі в цьому розділі. Щоб правильно трактувати це слово, згадайте характеристики ануїтетного платежу і визначте, чи відповідає ситуація критеріям. Розглянемо два приклади, що ілюструють цей момент:

Припустимо, Джон повинен Мері три платежі в розмірі 200 доларів через два місяці, п'ять місяців і одинадцять місяців. У цьому випадку слово «платіж» означає «єдиний платіж», оскільки платежі рівні (всі 200 доларів США), а періоди часу відомі, але вони не є ні періодичними (інтервали платежів нерівні), ні безперервними (оскільки періоди не існують, немає безперервності). Робота з цими платежами вимагає від вас застосування формул і прийомів з глави 9.
Припустимо, Джон повинен Джулії три платежі в розмірі 200 доларів через три місяці, шість місяців і дев'ять місяців. У цьому випадку слово «платіж» означає «аннуїтетний платіж», оскільки платежі бувають рівними (всі $200), періодичними (щокварталу) і безперервними (відбуваються щокварталу без перерви), і вони мають певні часові рамки (понад дев'ять місяців). Робота з цими платежами дозволяє застосовувати формули і прийоми з цього розділу.

Зрештою, коли ви сумніваєтеся, ви можете вирішити будь-яке питання, пов'язане з часом вартість грошей, використовуючи формули та методи з розділу 9. Формули ануїтету, введені в наступному розділі, просто дозволяють прийти до тієї ж відповіді з набагато меншим розрахунком.

Дописувачі та атрибуція

Template:ContribBusiMathOlivier