11.6: Відсоткові ставки ануїтету
- Page ID
- 66812
Canada One RV рекламує, що ви можете придбати причіп моделі парку Residence 40', вартістю $32,999, за $181.84 раз в два тижні протягом наступних 10 років. Торонто Hyundai пропонує «гарячу пропозицію Smokin» за $9900 Hyundai з 69 доларів щотижневих платежів протягом семи років. Зайшовши в Інтернет, ви відвідуєте веб-сайт 407 Express Toll Route (407 ETR), щоб подивитися на оплату дорожніх зборів на цьому шосе Торонто і побачити, що ви можете платити $21.50 щорічно або $3.25 на місяць. Перевіряючи реєстрацію автомобіля, ви бачите на веб-сайті страхування, що ви можете оплатити страхування мотоцикла одним платежем у розмірі 2,667 доларів США або п'ять платежів на початку місяця в розмірі 538 доларів США. Питання у всіх цих ситуаціях полягає в тому, чи варто платити все відразу або в розстрочку?
Зверніть увагу у всіх цих випадках, що загальна сума платежів вище, ніж ціна покупки товару. Наприклад, 407 ETR виставляє рахунок $3.25 на місяць, на загальну суму $39,00 на рік! З суворо фінансової точки зору, різниця від $21.50 може розглядатися як сума відсотків, що стягується за те, що не сплата повної річної суми заздалегідь. Але яку процентну ставку ви платите?
Інвестуючи, ви повинні вибрати найвищу ефективну ставку, яка несе рівень ризику, який ви можете прийняти. Якщо ви робите фіксовані внески в інвестицію, яку процентну ставку ви повинні отримати, щоб досягти своєї майбутньої мети? За боргами ви знаєте, що з вас стягують? Це ваші важко зароблені гроші, які ви витрачаєте, тому, можливо, ви можете знайти кращу пропозицію за нижчою ставкою від когось іншого? У бізнесі боргові відсотки - це витрати, які впливають на ціноутворення продукції і віднімаються з податку на прибуток. Щоб розрахувати відсотки, бізнесу потрібно знати процентну ставку, яку він нараховує.
У вас є багато причин, щоб розрахувати процентну ставку ануїтету. У цьому останньому розділі, присвяченому ануїтетам, ви зробите цей розрахунок як для звичайних ануїтетів, так і для належних ануїтетів
Звичайні ануїтети та ануїтети
Розрахувати процентну ставку по ануїтету необхідно в самих різних ситуаціях:
- Визначити процентну ставку, що нараховується по будь-якому боргу
- Визначити процентну ставку, яку заробляє інвестиція
- Розрахувати необхідну процентну ставку для економії, щоб досягти мети протягом певного часового періоду
- Для розрахунку необхідної процентної ставки, необхідної для ряду платежів, які будуть витримані протягом певного періоду часу
Типова шкала для невідомої процентної ставки по ануїтету відображається на малюнку нижче.

Всі змінні повинні бути відомі, крім номінальної процентної ставки,\(IY\). В будь-якому кінці часової шкали:
- Якщо ви знаєте\(PV_{DUE}\) або\(PV_{ORD}\), може бути\(FV\) на іншій стороні, а також. \(FV_{DUE}\),\(FV_{ORD}\), І не\(PV\) з'явиться.
- Якщо ви знаєте\(FV_{DUE}\) або\(FV_{ORD}\), може бути\(PV\) на іншій стороні. \(PV_{DUE}\),\(PV_{ORD}\), І не\(FV\) з'явиться.
Формула
Найцікавіша обставина виникає, коли ви намагаєтеся вирішити будь-яку формулу ануїтету майбутньої вартості або поточної вартості, як звичайну, так і належну, для процентної ставки. Формула 11.2 передрукована нижче для ілюстрації; однак, той самий пункт стосується формул 11.3 до 11.5.
\[\text { Formula } 11.2: FV_{ORD}=PMT\left[\dfrac{\left[(1+i)^{\frac{CY}{PY}}\right]^{N}-1}{(1+i)^{\frac{CY}{PY}}-1}\right] \nonumber \]
У цій формулі\(FV_{ORD}\)\(PMT\), або\(N\) кожен з'являється тільки один раз. Це дозволяє легко маніпулювати формулою для вирішення цих змінних, як ми це робили в попередніх розділах. Однак періодична процентна ставка\(i\), з'являється у формулі двічі. Зазвичай це не є проблемою, оскільки ви можете застосувати основні правила алгебри для виділення та поєднання подібних термінів, але не так у цьому випадку.
Щоб проілюструвати складність, призначте\(PMT\) = $1 і зробіть\(CY = PY\). Це робить рівняння наступним чином:
\[FV_{ORD}=\dfrac{(1+i)^N-1}{i} \nonumber \]
Якщо ви переставляєте формулу, яку ви маєте
\[iFV_{ORD}+1=(1+i)^N \nonumber \]
\(i\)На лівій стороні можна вільно ізолювати, але i з правого боку є частиною бази для експоненти. Щоб скасувати\(N\) показник, потрібно підняти обидві сторони рівняння до показника\(1/N\), доходячи до наступного:
\[\left(iFV_{ORD}+1\right)^{\frac{1}{N}}=1+i \nonumber \]
Зверніть увагу на результат: Тепер ліва сторона є\(i\) частиною бази для експоненти, тоді як\(i\) на правій стороні можна вільно ізолювати. Чи не багато поліпшення, чи не так? Щоб виправити це, вам потрібно буде взяти обидві сторони рівняння до показника\(N\), що повертає вас у вихідну дилему. Це нескінченний цикл без рішення.
Суть полягає в тому, що немає алгебраїчного способу виділити\(i\) в цьому рівнянні. Таким чином, ніяка перестановка формул 11.2 на 11.5 для виділення цієї змінної неможлива. Отже, як ви вирішуєте для цього? Є два способи:
- Проби і помилки. У цьому ручному методі ви просто продовжуєте підключати різні значення для\(i\) і намагатися додому на фактичне значення для змінної. Можливо, ви починаєте з\(i\) = 1% і дізнаєтеся,\(FV_{ORD}\) що ваш занадто низький. Потім ви спробуєте\(i\) = 2% і дізнаєтеся,\(FV_{ORD}\) що ваш занадто високий. Тепер ви знаєте, що i становить від 1% до 2%, тому, можливо, ви спробуєте 1,5%. Ви повторюєте цей процес, поки не закінчите з досить точним числом. Як ви можете собі уявити, цей процес надзвичайно трудомісткий, виснажливий і схильний до помилок, тому ніхто більше не виконує цей процес вручну.
- Використовуйте технологію. Незалежно від того, чи використовуєте ви калькулятори або електронні таблиці, ці інструменти попередньо запрограмовані методом проб і помилок і можуть виконати мільйони ітерацій менш ніж за секунду, щоб знайти рішення. Отже, всі проблеми в цьому розділі припускають, що у вас є доступ до технології, тому в розрахунках формул не відображаються алгебраїчні рішення.
Як це працює
Виконайте наступні дії, щоб вирішити будь-яку номінальну процентну ставку:
Крок 1: Визначте тип ануїтету. Намалюйте часову шкалу, щоб візуалізувати питання.
Крок 2: Визначте змінні, які ви знаєте, включаючи\(CY, PMT, PY\), і Years. Ви також повинні визначити значення для одного з\(PV_{ORD}\)\(PV_{DUE}\),\(FV_{ORD}\), або\(FV_{DUE}\). Ви можете або не мати значення для\(FV\) або\(PV\).
Крок 3: Використовуйте формулу 11.1 для обчислення N. Введіть всі шість відомих змінних у вашу технологію та вирішіть процентну ставку.
Важливі зауваження
Вирішення для номінальної процентної ставки на вашому BAII+вимагає ввести всі шість інших змінних, за винятком\(I/Y\). Потім натисніть CPT\(I/Y\), щоб вирішити проблему. Через техніку проб і помилок, ваш калькулятор може зайняти кілька секунд, щоб обчислити відповідь. Якщо ваш екран порожній і ваш калькулятор вагається, це нормально! Значення, які ви вводите в поточне значення (\(PV\)), майбутнє значення (\(FV\)) та ануїтетний платіж (\(PMT\)), повинні дотримуватися конвенції про знак грошового потоку. Пам'ятайте, що на BAII+,\(I/Y\) являє собою номінальну процентну ставку, яка складається відповідно до значення, яке ви ввели в\(C/Y\) змінну.
Речі, на які слід остерігатися
Вирішуючи по процентній ставці, зверніть пильну увагу на те, яка форма процентної ставки шукається:
- Періодичний (\(i\)): Що таке процентна ставка на місяць?
- Номінальна (\(IY\)з\(CY ≠ 1\)): Яка процентна ставка складається щомісяця?
- Ефективний (\(IY\)з\(CY = 1\)): Що таке щорічно складна або ефективна процентна ставка?
Шляхи до успіху
Якщо ви хочете знати як номінальну, так і ефективну процентну ставку в будь-якій ситуації, є два методи отримання відповідей. Першим кроком в обох методах є вирішення задачі номінальної процентної ставки з використанням відповідного значення для частоти компаундирования (\(CY\)). Тоді для розрахунку ефективної ставки можна виконати одну з наступних дій:
- \(CY\)Змініть на значення одиниці (\(CY = 1\)) і перерахуйте\(IY\). Ця книга віддає перевагу цьому методу, оскільки це простіший і менш схильний до помилок метод.
- Візьміть розраховану номінальну процентну ставку та перетворіть її на ефективну процентну ставку за допомогою Формули 9.4 (перетворення процентної ставки), калькулятора (функції I Conv) або шаблону Excel у розділі 9 (який використовує функцію EFFECT Excel). Ця техніка виробляє те саме базове рішення; однак, він має більший шанс помилки і може не вистачати точності, якщо використовується недостатньо десяткових знаків.
Чи можна у фінансових ситуаціях для розрахункового значення номінальної процентної ставки\(IY\), бути від'ємною?
- Відповідь
-
Так, це можливо. Багато інвестицій, таких як акції, коливаються залежно від ринкових умов. Можливо, що інвестиція втратить свою вартість після її придбання, що виробляє негативну норму прибутку.
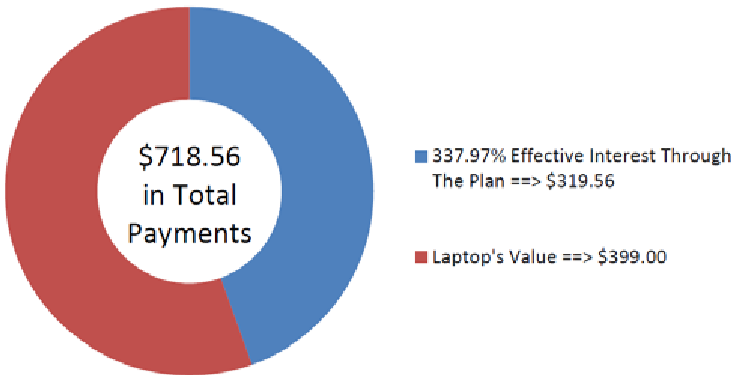
Smartchoice, оренда до власного магазину, пропонує Dell 10 «Mini Inspiron Netbook за готівку n' нести ціну $399. Крім того, за його планом оренди ви можете робити щомісячні платежі в розмірі 59.88 доларів заздалегідь та володіти ноутбуком через рік. Яка процентна ставка ефективно нараховується за планом оренди на власний?
Рішення
Крок 1:
Виплати здійснюються на початку інтервалів платежів, а період складання та інтервали виплат різні. Тому це загальна рента за рахунок. Вирішіть для ефективної процентної ставки, яка є номінальною процентною ставкою\(IY\), яка має частоту складання одиниці.
Що ви вже знаєте
Крок 1 (продовження):
Терміни для пенсійного ануїтету відображаються нижче.

Крок 2:
\(PV_{DUE}\)= $399,\(CY\) = 1,\(PMT\) = $59.88,\(PY\) = 12, років = 1
Як ви туди потрапите
Крок 3:
Застосовуємо Формулу 11.1 і Формулу 11.5. Введіть інформацію в калькулятор для вирішення\(IY\) (який автоматично застосовує формулу 9.1 для перетворення\(i\) в\(IY\)).
Виконувати
Крок 3:
\(N=12 \times 1=12\)платежі
\[\$ 399=\$ 59.88\left[\dfrac{1-\left[\dfrac{1}{(1+i)^{\frac{1}{12}}}\right]^{12}}{(1+i)^{\frac{1}{12}}-1}\right] \times(1+i) \frac{1}{12} \nonumber \]
Дивіться інструкцію калькулятора для рішення.
Інструкції з калькулятора
| Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| ЛВ | 12 | Відповідь: 337.975924 | 399 | -59.88 | 0 | 12 | 1 |
На малюнку показані ефективні відсотки і вартість ноутбука, які складають виплати. Ефективна процентна ставка, що нараховується за планом оплати орендної плати, становить 337,9759%.
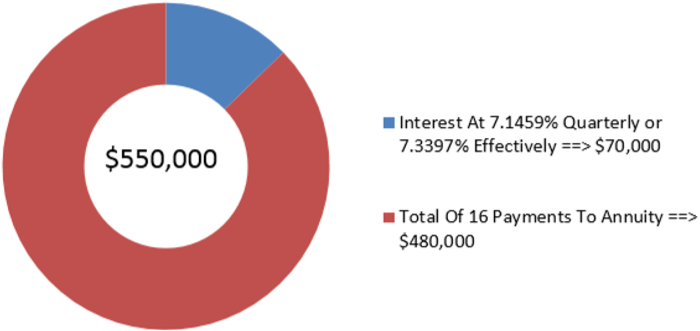
Cubonic Industries депозити $30,000 наприкінці кожного кварталу, щоб заощадити 550 000 доларів на капітальний проект протягом чотирьох років. Для досягнення своєї мети, яка номінальна процентна ставка, що складається щоквартально, вимагає Cubonic Industries для своїх інвестицій? Яка ефективна ставка?
Рішення
Крок 1:
Тут є два питання. Перше питання про номінальну процентну ставку передбачає звичайний простий ануїтет. Вирішіть це для\(IY\) коли\(CY\) = 4. Друге питання про ефективну ставку передбачає звичайну загальну ануїтет. Вирішіть це для\(IY\) коли\(CY\) = 1.
Що ви вже знаєте
Крок 1 (продовження):
Хронологія для обох питань відображається нижче.

Крок 2:
Звичайний простий ануїтет:\(FV_{ORD}\) = 550 000 доларів,\(CY\) = 4,\(PMT\) = 30 000 доларів,\(PY\) = 4, років = 4
Звичайний загальний ануїтет: Все те ж саме, крім\(CY\) = 1
Як ви туди потрапите
Крок 3:
Застосовуємо Формулу 11.1 і Формулу 11.2.
Звичайний простий ануїтет: Введіть інформацію в калькулятор і вирішіть для\(IY\).
Звичайний загальний ануїтет:\(CY\) Змініть на 1 (для ефективної ставки) та перерахуйте\(IY\). Зверніть увагу, що для обох ануїтетів калькулятор автоматично застосовує формулу 9.1 для перетворення\(i\) в\(IY\).
Виконувати
Крок 3:
\(N=4 \times 4=16\)платежі
Звичайний простий ануїтет:
\[\$ 550,000=\$ 30,000\left[\dfrac{\left[(1+i)^{\frac{4}{4}}\right]^{16}-1}{(1+i)^{\frac{4}{4}}-1}\right] \nonumber \]
Звичайний загальний ануїтет:
\[\$ 550,000=\$ 30,000\left[\dfrac{\left[(1+i)^{\frac{1}{4}}\right]^{16}-1}{(1+i)^{\frac{1}{4}}-1}\right] \nonumber \]
Дивіться інструкції калькулятора нижче для вирішення кожного питання.
Інструкції з калькулятора
| Тип | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| Простий | 16 | Відповідь: 7.145908 | 0 | -30000 | 550000 | 4 | 4 |
| Загальний | \(\surd\) | Відповідь: 7.339689 | \(\surd\) | \(\surd\) | \(\surd\) | \(\surd\) | 1 |
На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Для того, щоб Cubonic Industries досягти своєї мети заощаджень, рента заощаджень повинна заробляти 7.1459%, що складається щоквартально, або 7.3397% ефективно.
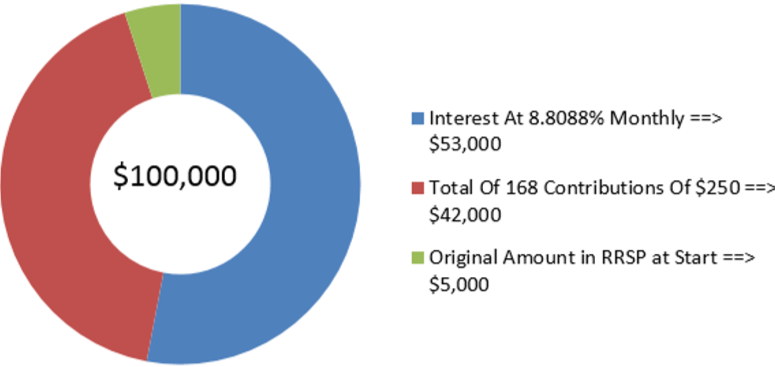
Амадей вже заощадив 5000 доларів у своєму RRSP сьогодні. Припустимо, він продовжує робити 250 доларів на початку кожного місяця протягом наступних 14 років. Щоб він досяг своєї мети мати 100 000 доларів, яку щомісячну номінальну норму прибутку повинні заробляти його інвестиції?
Рішення
Крок 1:
Виплати здійснюються на початку інтервалів платежів, а період складання та інтервали виплат однакові. Тому це проста рента за рахунок. Вирішити за щомісячну номінальну процентну ставку,\(IY\).
Що ви вже знаєте
Крок 1 (продовження):
Хронологія внесків RRSP відображається нижче.

Крок 2:
\(FV_{DUE}\)= $100 000,\(PV\) = $5,000,\(CY\) =12,\(PMT\) = $250,\(PY\) = 12, років = 14
Як ви туди потрапите
Крок 3:
Застосовуємо Формулу 11.1 і калькулятор одночасно вирішує формули 9.3 і 11.3. Аннуїтет простий, тому\(N\) однакова кількість як для кількості платежів, так і для складів. Введіть інформацію в калькулятор і вирішіть для\(IY\).
Виконувати
Крок 3:
\(N=12 \times 14=168\)платежі
\[\$ 100,000-\$ 5,000(1+i)^{168}=\$ 250\left[\dfrac{\left[(1+i)^{\frac{12}{12}}\right]^{168}-1}{(1+i)^{\frac{12}{12}}-1}\right] \times(1+i)^{\frac{12}{12}} \nonumber \]
Дивіться інструкцію калькулятора для рішення.
Інструкції з калькулятора
| Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| ЛВ | 168 | Відповідь: 8.808808 | -5000 | -250 | 100000 | 12 | 12 |
На малюнку видно, скільки основного боргу і відсотків складають остаточний баланс. Номінальна процентна ставка, яку Амадей повинен заробляти на своїх інвестиціях, становить 8,8088%, що складається щомісяця.
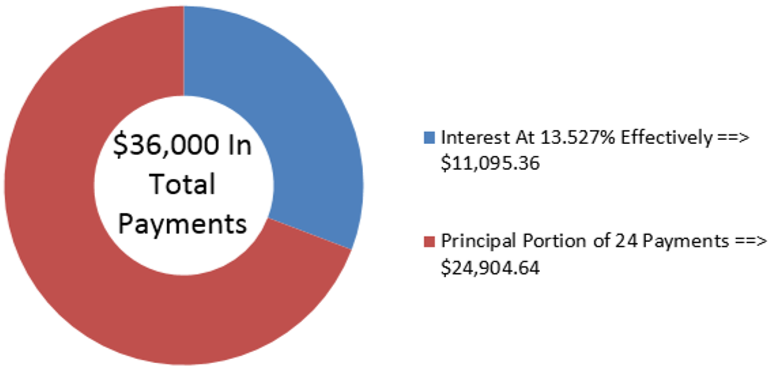
Джемма хоче придбати новий Nissan Pathfinder за $54 904,64, включаючи всі збори та податки з продажу. Вона може дозволити собі платити не більше 1500 доларів наприкінці кожного місяця, і вона хоче, щоб через два роки залишок зменшився до 30 000 доларів, коли вона зможе погасити транспортний засіб своїм цільовим фондом. Яку максимальну ефективну ставку відсотків вона могла б нараховувати по автокредиту для досягнення своїх цілей?
Рішення
Крок 1:
Виплати здійснюються в кінці інтервалів платежів, а період складання та інтервали платежів різні. Тому це звичайна загальна ануїтет. Вирішити для ефективної процентної ставки,\(IY\).
Що ви вже знаєте
Крок 1 (продовження):
Графік оформлення автокредиту відображається нижче.

Крок 2:
\(PV_{ORD}\)= $54 904,64,\(FV\) = $30,000,\(CY\) =1,\(PMT\) = $1,500,\(PY\) = 12, років = 2
Як ви туди потрапите
Крок 3:
Застосовуємо Формулу 11.1, і калькулятор одночасно вирішує формули 9.3 і 11.4. * Зверніть увагу, що оскільки ануїтет є загальним,\(N\) з'єднання та\(N\) платежі мають різні цифри. Покладання цих двох елементів в одне і те ж рівняння вимагає, щоб\(N\) взяти на себе єдине значення, що дорівнює кількості платежів (вимога ануїтету). У зв'язку з цим періодична процентна ставка, яка використовується у Формулі 9.3, повинна бути перетворена відповідно до частоти виплат. Ви досягаєте цього за допомогою того ж\(\dfrac{CY}{PY}\) показника з ануїтетів формул. Введіть інформацію в калькулятор і вирішіть для\(IY\).
Виконувати
Крок 3:
\(N=12 \times 2=24\)платежі
\[\$ 54,904.64-\dfrac{\$ 30,000}{\left[(1+i)^{\frac{1}{12}}\right]^{24}}=\$ 1,500\left[\dfrac{1-\left[\frac{1}{(1+i)^{\frac{1}{12}}}\right]^{24}}{(1+i)^{\frac{1}{12}}-1}\right] \nonumber \]
Дивіться інструкцію калькулятора для рішення.
Інструкції з калькулятора
| П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|
| 24 | Відповідь: 13.527019 | 549.04.64 | -1500 | -30000 | 12 | 1 |
На малюнку видно, скільки основного боргу і відсотків складають виплати. Джемма зможе придбати автомобіль, якщо зможе отримати автокредит, який має ефективну процентну ставку нижче 13,527%.