4.7: Точковий продукт

Результати

1. Обчислити точковий добуток векторів і використовувати його для обчислення векторних проекцій.

Точковий продукт

Існує два способи множення векторів, які мають велике значення в додатках. Перший з них називається точковим добутком. Коли ми беремо точковий добуток векторів, результат є скалярним. З цієї причини крапковий добуток також називають скалярним добутком, а іноді і внутрішнім твором. Визначення таке.

Визначення\(\PageIndex{1}\): Dot Product

\(\vec{u},\vec{v}\)Дозволяти два вектори в\(\mathbb{R}^{n}\). Потім ми визначаємо точковий добуток\(\vec{u}\bullet \vec{v}\) як\[\vec{u}\bullet \vec{v} = \sum_{k=1}^{n}u_{k}v_{k}\nonumber \]

Точковий\(\vec{u}\bullet \vec{v}\) добуток іноді позначається як\((\vec{u},\vec{v})\) місце, де замінює кома\(\bullet\). Його також можна записати як\(\left\langle \vec{u},\vec{v}\right\rangle\). Якщо ми запишемо вектори у вигляді матриць стовпців або рядків, то він дорівнює добутку матриці\(\vec{v}\vec{w}^{T}\).

Розглянемо наступний приклад.

Приклад\(\PageIndex{1}\): Compute a Dot Product

Знайти\(\vec{u} \bullet \vec{v}\) для\[\vec{u} = \left[ \begin{array}{r} 1 \\ 2 \\ 0 \\ -1 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 0 \\ 1 \\ 2 \\ 3 \end{array} \right]\nonumber \]

Рішення

За визначенням\(\PageIndex{1}\), ми повинні обчислити\[\vec{u}\bullet \vec{v} = \sum_{k=1}^{4}u_{k}v_{k}\nonumber \]

Це дається\[\begin{aligned} \vec{u} \bullet \vec{v} &= (1)(0) + (2)(1) + (0)(2) + (-1)(3) \\ &= 0 + 2 + 0 + -3 \\ &= -1\end{aligned}\]

При такому визначенні існує кілька важливих властивостей, які задовольняє точковий добуток.

Пропозиція\(\PageIndex{1}\): Properties of the Dot Product

Нехай\(k\) і\(p\) позначають скалярами і\(\vec{u},\vec{v},\vec{w}\) позначають вектори. Тоді точковий твір\(\vec{u} \bullet \vec{v}\) задовольняє наступним властивостям.

• \(\vec{u}\bullet \vec{v}= \vec{v}\bullet \vec{u}\)
• \(\vec{u}\bullet \vec{u}\geq 0 \text{ and equals zero if and only if }\vec{u}=\vec{0}\)
• \(\left( k\vec{u}+p\vec{v}\right) \bullet \vec{w}=k\left( \vec{u}\bullet \vec{w}\right) +p\left( \vec{v}\bullet \vec{w}\right)\)
• \(\vec{u}\bullet\left( k\vec{v}+p\vec{w}\right) =k\left( \vec{u}\bullet \vec{v}\right) +p\left( \vec{u}\bullet \vec{w}\right)\)
• \(\| \vec{u}\| ^{2}=\vec{u}\bullet \vec{u}\)

Доказ

Доказ залишають як вправу.

Ця пропозиція говорить нам, що ми також можемо використовувати точковий добуток, щоб знайти довжину вектора.

Приклад\(\PageIndex{2}\): Length of a Vector

Знайти довжину\[\vec{u} = \left[ \begin{array}{r} 2 \\ 1 \\ 4 \\ 2 \end{array} \right]\nonumber \] Тобто, знайти\(\| \vec{u} \| .\)

Рішення

За пропозицією\(\PageIndex{1}\),\(\| \vec{u} \| ^{2} = \vec{u} \bullet \vec{u}\). Тому,\(\| \vec{u} \| = \sqrt {\vec{u} \bullet \vec{u}}\). По-перше, обчислюйте\(\vec{u} \bullet \vec{u}\).

Це дається\[\begin{aligned} \vec{u} \bullet \vec{u} &= (2)(2) + (1)(1) + (4)(4) + (2)(2) \\ &= 4 + 1 + 16 + 4 \\ &= 25\end{aligned}\]

Потім,\[\begin{aligned} \| \vec{u} \| &= \sqrt {\vec{u} \bullet \vec{u}} \\ &= \sqrt{25} \\ &= 5\end{aligned}\]

Ви можете порівняти це з нашим попереднім визначенням довжини, наведеним у Визначенні 4.4.2.

Нерівність Коші Шварца - це фундаментальна нерівність, задоволена точковим добутком. Він наведено в наступній теоремі.

Теорема\(\PageIndex{1}\): Cauchy Schwarz Inequality

Точковий добуток задовольняє нерівність\[\left\vert \vec{u}\bullet \vec{v}\right\vert \leq \| \vec{u}\| \| \vec{v}\| \label{cauchy}\] Крім того рівність виходить тоді і тільки тоді, коли один з\(\vec{u}\) або\(\vec{v}\) є скалярним кратним іншому.

Доказ

По-перше, зауважте, що якщо\(\vec{v}=\vec{0}\) обидві сторони\(\eqref{cauchy}\) дорівнюють нулю і так нерівність тримається в цьому випадку. Тому буде припускатися, що випливає з цього\(\vec{v}\neq \vec{0}\).

Визначте функцію\(t\in \mathbb{R}\) by\[f\left( t\right) =\left( \vec{u}+t\vec{v}\right) \bullet \left( \vec{u}+ t\vec{v}\right)\nonumber \] Then by Proposition\(\PageIndex{1}\),\(f\left( t\right) \geq 0\) для всіх\(t\in \mathbb{R}\). Також з пропозиції\(\PageIndex{1}\)\[\begin{aligned} f\left( t\right) &=\vec{u}\bullet \left( \vec{u}+t\vec{v}\right) + t\vec{v}\bullet \left( \vec{u}+t\vec{v}\right) \\ &=\vec{u}\bullet \vec{u}+t\left( \vec{u}\bullet \vec{v}\right) + t \vec{v}\bullet \vec{u}+ t^{2}\vec{v}\bullet \vec{v} \\ &=\| \vec{u}\| ^{2}+2t\left( \vec{u}\bullet \vec{v}\right) +\| \vec{v}\| ^{2}t^{2}\end{aligned}\]

Тепер це означає, що граф\(y=f\left( t\right)\) є параболою, яка відкривається і або його вершина торкається\(t\) осі, або весь графік знаходиться над\(t\) віссю. У першому випадку існує деяка,\(t\) де\(f\left( t\right) =0\) і для цього потрібно,\(\vec{u}+t\vec{v}=\vec{0}\) щоб один вектор був кратний іншому. Тоді явно рівність тримається в\(\eqref{cauchy}\). У випадку, коли\(\vec{v}\) не кратна\(\vec{u}\), це випливає\(f\left( t\right) >0\) за все,\(t\) що говорить, не\(f\left( t\right)\) має реальних нулів і так з квадратичної формули,\[\left( 2\left( \vec{u}\bullet \vec{v}\right) \right) ^{2}-4\| \vec{u} \| ^{2}\| \vec{v}\| ^{2}<0\nonumber \] яка еквівалентна\(\left\vert \vec{u}\bullet \vec{v} \right\vert <\| \vec{u}\| \| \vec{v}\|\).

Зверніть увагу, що цей доказ базувався лише на властивостях крапкового добутку, переліченого у Пропозиції\(\PageIndex{1}\). Це означає, що всякий раз, коли операція задовольняє цим властивостям, нерівність Коші Шварца тримається. Існує багато інших примірників цих властивостей, крім векторів в\(\mathbb{R}^{n}\).

Нерівність Коші Шварца дає ще один доказ нерівності трикутника для відстаней в\(\mathbb{R}^{n}\).

Теорема\(\PageIndex{2}\): Triangle Inequality

Для\(\vec{u},\vec{v}\in \mathbb{R}^{n}\)\[\| \vec{u}+\vec{v}\| \leq \| \vec{u}\| +\| \vec{v} \| \label{triangleineq1}\] і рівність тримає тоді і лише тоді, коли один із векторів є невід'ємним скалярним кратним іншому.

Також\[\| \| \vec{u}\| -\| \vec{v}\| \| \leq \| \vec{u}-\vec{v}\| \label{triangleineq2}\]

Доказ

За властивостями точкового добутку і нерівності Коші Шварца,\[\begin{aligned} \| \vec{u}+\vec{v}\| ^{2} &= \left( \vec{u}+\vec{v}\right) \bullet \left( \vec{u}+\vec{v}\right) \\ & =\left( \vec{u}\bullet \vec{u}\right) +\left( \vec{u}\bullet \vec{v}\right) +\left(\vec{v}\bullet \vec{u}\right) +\left( \vec{v}\bullet \vec{v}\right) \\ &=\| \vec{u}\| ^{2}+2\left( \vec{u}\bullet \vec{v}\right)+\| \vec{v}\| ^{2} \\ &\leq \| \vec{u}\| ^{2}+2\left\vert \vec{u}\bullet \vec{v}\right\vert +\| \vec{v}\| ^{2} \\ &\leq \| \vec{u}\| ^{2}+2\| \vec{u}\| \| \vec{v}\| +\| \vec{v}\| ^{2} =\left( \| \vec{u}\| +\| \vec{v}\|\right) ^{2}\end{aligned}\] Отже,\[\| \vec{u}+\vec{v}\| ^{2} \leq \left( \| \vec{u}\| +\| \vec{v}\| \right) ^{2}\nonumber \] Беручи квадратні корені з обох сторін ви отримаєте\(\eqref{triangleineq1}\).

Залишається розглянути, коли відбувається рівність. Припустимо\(\vec{u} = \vec{0}\). Потім\(\vec{u} = 0 \vec{v}\) і твердження про те, коли відбувається рівність, перевіряється. Той самий аргумент має значення if\(\vec{v} = \vec{0}\). Тому можна припустити, що обидва вектора ненульові. Щоб отримати рівність\(\eqref{triangleineq1}\) вище, Теорема\(\PageIndex{1}\) передбачає, що один з векторів повинен бути кратним іншому. Скажи\(\vec{v}= k \vec{u}\). Якщо\(k <0\) тоді рівність не може відбутися,\(\eqref{triangleineq1}\) тому що в цьому випадку\[\vec{u}\bullet \vec{v} =k \| \vec{u}\| ^{2}<0<\left| k \right| \| \vec{u}\| ^{2}=\left| \vec{u}\bullet \vec{v}\right|\nonumber \] Отже,\(k \geq 0.\)

Щоб отримати іншу форму нерівності трикутника пишіть\[\vec{u}=\vec{u}-\vec{v}+\vec{v}\nonumber \] так\[\begin{aligned} \| \vec{u}\| & =\| \vec{u}-\vec{v}+\vec{v}\| \\ & \leq \| \vec{u}-\vec{v}\| +\| \vec{v}\| \end{aligned}\] Тому,\[\| \vec{u}\| -\| \vec{v}\| \leq \| \vec{u}-\vec{v} \| \label{triangleineq3}\] Аналогічно,\[\| \vec{v}\| -\| \vec{u}\| \leq \| \vec{v}-\vec{u} \| =\| \vec{u}-\vec{v}\| \label{triangleineq4}\] випливає з\(\eqref{triangleineq3}\) і\(\eqref{triangleineq4}\) що\(\eqref{triangleineq2}\) тримає. Це тому, що\(\left| \| \vec{u}\| -\| \vec{v}\| \right|\) дорівнює лівій стороні\(\eqref{triangleineq3}\) або або\(\eqref{triangleineq4}\) і в будь-якому випадку,\(\left| \| \vec{u}\| -\| \vec{v}\| \right| \leq \| \vec{u}-\vec{v}\|\).

Геометричне значення точкового добутку

Задано два вектори,\(\vec{u}\) і\(\vec{v}\), включений кут є кутом між цими двома векторами, який задається\(\theta\) таким, що\(0 \leq \theta \leq \pi\). Точковий добуток може бути використаний для визначення включеного кута між двома векторами. Розглянемо наступну картину, де\(\theta\) дає включений кут.

Малюнок\(\PageIndex{1}\)

Пропозиція\(\PageIndex{2}\): The Dot Product and the Included Angle

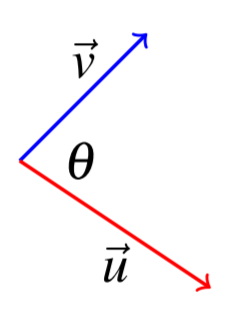
\(\vec{u}\)\(\vec{v}\)Дозволяти і бути два вектори в\(\mathbb{R}^n\), і нехай\(\theta\) бути включений кут. Потім проводиться наступне рівняння. \[\vec{u}\bullet \vec{v}=\| \vec{u}\| \| \vec{v} \| \cos \theta\nonumber \]

У словах крапковий добуток двох векторів дорівнює добутку величини (або довжини) двох векторів, помножених на косинус включеного кута. Зауважте, що це дає геометричний опис крапкового добутку, який явно не залежить від координат векторів.

Розглянемо наступний приклад.

Приклад\(\PageIndex{3}\): Find the Angle Between Two Vectors

Знайти кут між векторами, заданими\[\vec{u} = \left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ 4 \\ 1 \end{array} \right]\nonumber \]

Рішення

За пропозицією\(\PageIndex{2}\),\[\vec{u}\bullet \vec{v}=\| \vec{u}\| \| \vec{v} \| \cos \theta\nonumber \] отже,\[\cos \theta =\frac{\vec{u}\bullet \vec{v}}{\| \vec{u}\| \| \vec{v} \|}\nonumber \]

По-перше, ми можемо обчислити\(\vec{u}\bullet \vec{v}\). За \(\PageIndex{1}\)визначенням це дорівнює\[\vec{u}\bullet \vec{v} = (2)(3) + (1)(4)+(-1)(1) = 9\nonumber \]

Тоді,\[\begin{array}{c} \| \vec{u} \| = \sqrt{(2)(2)+(1)(1)+(1)(1)}=\sqrt{6}\\ \| \vec{v} \| = \sqrt{(3)(3)+(4)(4)+(1)(1)}=\sqrt{26} \end{array}\nonumber \] отже, косинус включеного кута дорівнює\[\cos \theta =\frac{9}{\sqrt{26}\sqrt{6}}=0.7205766...\nonumber \]

При відомому косинусі кут можна визначити, обчисливши обернений косинус цього кута, даючи приблизно\(\theta =0.76616\) радіани.

Ще одне застосування геометричного опису точкового добутку полягає у знаходженні кута між двома лініями. Зазвичай можна вважати, що лінії перетинаються. У деяких ситуаціях, однак, може мати сенс задати це питання, коли лінії не перетинаються, наприклад, кут між двома траєкторіями об'єкта. У будь-якому випадку ми розуміємо, що це означає найменший кут між (будь-яким з) векторів напрямків. Єдина тонкість тут полягає в тому, що якщо\(\vec{u}\) вектор напрямку для прямої, то так і будь-який кратний, і\(k\vec{u}\), таким чином, ми знайдемо взаємодоповнюючі кути серед усіх кутів між векторами напрямків для двох ліній, і ми просто візьмемо менший з двох.

Приклад\(\PageIndex{4}\): Find the Angle Between Two Lines

Знайти кут між двома лініями\[L_1: \; \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{r} 1 \\ 2 \\ 0 \end{array} \right] +t\left[ \begin{array}{r} -1 \\ 1 \\ 2 \end{array} \right]\nonumber \] і\[L_2: \; \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{r} 0 \\ 4 \\ -3 \end{array} \right] +s\left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right]\nonumber \]

Рішення

Ви можете переконатися, що ці лінії не перетинаються, але, як обговорювалося вище, це не має значення, і ми просто знаходимо найменший кут між будь-якими напрямками векторів для цих ліній.

Для цього спочатку знайдемо кут між векторами напрямків, наведеними вище:\[\vec{u}=\left[ \begin{array}{r} -1 \\ 1 \\ 2 \end{array} \right],\; \vec{v}=\left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right]\nonumber \]

Для того, щоб знайти кут, ми вирішуємо наступне рівняння для\(\theta\)\[\vec{u}\bullet \vec{v}=\| \vec{u}\| \| \vec{v} \| \cos \theta\nonumber \] отримання,\(\cos \theta = -\frac{1}{2}\) і оскільки ми вибираємо включені кути між ними\(0\) і\(\pi\) отримуємо\(\theta = \frac{2 \pi}{3}\).

Тепер кути між будь-якими двома векторами напрямків для цих ліній будуть\(\frac{2 \pi}{3}\) або їх доповненням\(\phi = \pi - \frac{2 \pi}{3} = \frac{\pi}{3}\). Вибираємо менший кут, і тому робимо висновок, що кут між двома лініями є\(\frac{\pi}{3}\).

Ми також можемо використовувати Proposition\(\PageIndex{2}\) для обчислення крапкового добутку двох векторів.

Приклад\(\PageIndex{5}\): Using Geometric Description to Find a Dot Product

\(\vec{u},\vec{v}\)Дозволяти бути вектори з\(\| \vec{u} \| = 3\) і\(\| \vec{v} \| = 4\). Припустимо, кут між\(\vec{u}\) і\(\vec{v}\) є\(\pi / 3\). Знайти\(\vec{u}\bullet \vec{v}\).

Рішення

З геометричного опису крапкового добутку в Пропозиції\(\PageIndex{2}\)\[\vec{u}\bullet \vec{v}=(3)(4) \cos \left( \pi / 3\right) =3\times 4\times 1/2=6\nonumber \]

Кажуть, що два ненульові вектори перпендикулярні, іноді їх також називають ортогональними, якщо включений кут є\(\pi /2\) радіанами (\(90^{\circ }).\)

Розглянемо наступну пропозицію.

Пропозиція\(\PageIndex{3}\): Perpendicular Vectors

\(\vec{v}\)Дозволяти\(\vec{u}\) і бути ненульові вектори в\(\mathbb{R}^n\). Потім,\(\vec{u}\) і, як\(\vec{v}\) кажуть, перпендикулярно точно, коли\[\vec{u} \bullet \vec{v} = 0\nonumber \]

Доказ

Це випливає безпосередньо з Пропозиції\(\PageIndex{2}\). По-перше, якщо крапковий добуток двох ненульових векторів дорівнює\(0\), це говорить нам про те, що\(\cos \theta =0\) (тут нам потрібні ненульові вектори). Таким чином\(\theta = \pi /2\) і вектори перпендикулярні.

Якщо з іншого боку\(\vec{v}\) перпендикулярно\(\vec{u}\), то включений кут -\(\pi /2\) радіани. Звідси\(\cos \theta =0\) і\(\vec{u} \bullet \vec{v} = 0\).

Розглянемо наступний приклад.

Приклад\(\PageIndex{6}\): Determine if Two Vectors are Perpendicular

Визначте, чи два вектори,\[\vec{u}= \left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 1 \\ 3 \\ 5 \end{array} \right]\nonumber \] перпендикулярні.

Рішення

Для того, щоб визначити, чи є ці два вектори перпендикулярними, обчислюємо точковий добуток. Це дається\[\vec{u} \bullet \vec{v} = (2)(1) + (1)(3) + (-1)(5) = 0\nonumber \] Отже, Пропозиція\(\PageIndex{3}\) ці два вектори перпендикулярні.

Проекції

У деяких додатках ми хочемо написати вектор у вигляді суми двох пов'язаних векторів. Через концепцію проекцій ми можемо знайти ці два вектори. Спочатку досліджуємо важливу теорему. Результат цієї теореми забезпечить наше визначення векторної проекції.

Теорема\(\PageIndex{3}\): Vector Projections

\(\vec{u}\)Дозволяти\(\vec{v}\) і бути ненульовими векторами. Тоді існують унікальні вектори\(\vec{v}_{||}\) і\(\vec{v}_{\bot }\) такі, що\[\vec{v}=\vec{v}_{||}+\vec{v}_{\bot } \label{projection}\] де\(\vec{v}_{||}\) скалярний кратний\(\vec{u}\), і\(\vec{v}_{\bot}\) перпендикулярно\(\vec{u}\).

Доказ

Припустимо,\(\eqref{projection}\) тримає і\(\vec{v}_{||}= k \vec{u}\). Беручи крапковий добуток обох сторін\(\eqref{projection}\)\(\vec{u}\) with і використання\(\vec{v}_{\bot }\bullet \vec{u}=0,\) цього дає\[\begin{array}{ll} \vec{v}\bullet \vec{u} & = ( \vec{v}_{||}+\vec{v}_{\bot }) \bullet \vec{u} \\ & = k\vec{u} \bullet \vec{u} + \vec{v}_{\bot} \bullet \vec{u} \\ & = k \| \vec{u}\| ^{2} \end{array}\nonumber \], що вимагає\(k =\vec{v}\bullet \vec{u} / \| \vec{u}\| ^{2}.\) Таким чином, може бути не більше одного вектора\(\vec{v}_{||}\). Випливає,\(\vec{v}_{\bot }\) повинен рівнятися\(\vec{v}-\vec{v}_{||}.\) Це перевіряє, що не може бути більше одного вибору для обох\(\vec{v}_{||}\)\(\vec{v}_{\bot }\) і доводить їх унікальність.

Тепер нехай\[\vec{v}_{||} = \frac{\vec{v}\bullet \vec{u}}{\| \vec{u}\| ^{2}}\vec{u}\nonumber \] і нехай\[\vec{v}_{\bot }=\vec{v}-\vec{v}_{||}=\vec{v}-\frac{\vec{v}\bullet \vec{u}} {\| \vec{u}\| ^{2}}\vec{u}\nonumber \] Тоді\(\vec{v}_{||}= k\vec{u}\) куди\(k =\frac{\vec{v}\bullet \vec{u}}{\| \vec{u}\| ^{2}}\). Залишилося лише перевірити\(\vec{v}_{\bot }\bullet \vec{u}=0.\) Але\[\begin{aligned} \vec{v}_{\bot }\bullet \vec{u} &= \vec{v}\bullet \vec{u}-\frac{\vec{v}\bullet \vec{u}}{\| \vec{u}\| ^{2}}\vec{u}\bullet \vec{u} \\ &= \vec{v}\bullet\vec{u}-\vec{v}\bullet \vec{u}\\ &= 0 \end{aligned}\]

Вектор\(\vec{v}_{||}\) в теоремі\(\PageIndex{3}\) називається \(\vec{v}\)проекцією на\(\vec{u}\) і позначається\[\vec{v}_{||} = \mathrm{proj}_{\vec{u}}\left( \vec{v}\right)\nonumber \]

Тепер зробимо формальне визначення векторної проекції.

Визначення\(\PageIndex{2}\): Vector Projection

\(\vec{v}\)Дозволяти\(\vec{u}\) і бути вектори. Потім проекція\(\vec{v}\) на\(\vec{u}\) задається\[\mathrm{proj}_{\vec{u}}\left( \vec{v}\right) =\left( \frac{\vec{v}\bullet \vec{u}}{\vec{u}\bullet \vec{u}}\right) \vec{u} = \frac{\vec{v}\bullet \vec{u}}{\| \vec{u}\| ^{2}}\vec{u}\nonumber \]

Розглянемо наступний приклад проекції.

Приклад\(\PageIndex{7}\): Find the Projection of One Vector Onto Another

Знайти,\(\mathrm{proj}_{\vec{u}}\left( \vec{v}\right)\) якщо\[\vec{u}= \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right], \vec{v}= \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right]\nonumber \]

Рішення

Ми можемо використовувати формулу, надану у Визначенні\(\PageIndex{2}\), щоб знайти\(\mathrm{proj}_{\vec{u}}\left( \vec{v}\right)\). По-перше, обчислюйте\(\vec{v} \bullet \vec{u}\). Це дається\[\begin{aligned} \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right] \bullet \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right] &= (2)(1) + (3)(-2) + (-4)(1) \\ &= 2 - 6 - 4 \\ &= -8\end{aligned}\] аналогічно,\(\vec{u} \bullet \vec{u}\) дається\[\begin{aligned} \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right] \bullet \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right] &= (2)(2) + (3)(3) + (-4)(-4) \\ &= 4 + 9 + 16 \\ &= 29\end{aligned}\]

Тому проекція дорівнює\[\begin{aligned} \mathrm{proj}_{\vec{u}}\left( \vec{v}\right) &=-\frac{8}{29} \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right] \\ &= \left[ \begin{array}{r} - \frac{16}{29} \\ - \frac{24}{29} \\ \frac{32}{29} \end{array} \right]\end{aligned}\]

Завершимо цей розділ важливим застосуванням проекцій. Припустимо, лінія\(L\) і точка задані\(P\) такі, які\(P\) не містяться в\(L\). За допомогою використання проекцій ми можемо визначити найкоротшу відстань від\(P\) до\(L\).

Приклад\(\PageIndex{8}\): Shortest Distance from a Point to a Line

\(P = (1,3,5)\)Дозволяти точка в\(\mathbb{R}^3\), і\(L\) нехай лінія, яка проходить через точку\(P_0 = (0,4,-2)\) з напрямком вектора\(\vec{d} = \left[ \begin{array}{r} 2 \\ 1 \\ 2 \end{array} \right]\). Знайдіть найкоротшу відстань від\(P\) до лінії\(L\), і знайдіть точку\(Q\) на\(L\) якій найближче до\(P\).

Рішення

Для того, щоб визначити найкоротшу відстань від\(P\) до\(L\), спочатку знайдемо вектор,\(\overrightarrow{P_0P}\) а потім знайдемо проекцію цього вектора на\(L\). \(\overrightarrow{P_0P}\)Вектор задається\[\left[ \begin{array}{r} 1 \\ 3 \\ 5 \end{array} \right] - \left[ \begin{array}{r} 0 \\ 4 \\ -2 \end{array} \right] = \left[ \begin{array}{r} 1 \\ -1 \\ 7 \end{array} \right]\nonumber \]

Потім, якщо\(Q\) точка на\(L\) найближче до\(P\), випливає, що\[\begin{aligned} \overrightarrow{P_0Q} &= \mathrm{proj}_{\vec{d}}\overrightarrow{P_0P} \\ &= \left( \frac{ \overrightarrow{P_0P}\bullet \vec{d}}{\|\vec{d}\|^2}\right) \vec{d} \\ &= \frac{15}{9} \left[ \begin{array}{r} 2 \\ 1 \\ 2 \end{array} \right] \\ &= \frac{5}{3} \left[ \begin{array}{r} 2 \\ 1 \\ 2 \end{array} \right]\end{aligned}\]

Тепер відстань від\(P\) до\(L\) задається\[\| \overrightarrow{QP} \| = \| \overrightarrow{P_0P} - \overrightarrow{P_0Q}\| = \sqrt{26}\nonumber \]

\(Q\)Точка знаходить шляхом додавання вектора\(\overrightarrow{P_0Q}\) до вектора\(\overrightarrow{0P_0}\) положення\(P_0\) наступним чином\[\begin{aligned} \left[ \begin{array}{r} 0 \\ 4 \\ -2 \end{array} \right] + \frac{5}{3} \left[ \begin{array}{r} 2 \\ 1 \\ 2 \end{array} \right] &= \left[ \begin{array}{r} \frac{10}{3} \\ \frac{17}{3} \\ \frac{4}{3} \end{array} \right]\end{aligned}\]

Тому,\(Q = (\frac{10}{3}, \frac{17}{3}, \frac{4}{3})\).