12.3: Точковий продукт
- Page ID
- 61525
- Обчислити точковий добуток двох заданих векторів.
- Визначте, чи два задані вектори перпендикулярні.
- Знайдіть косинуси напряму заданого вектора.
- Поясніть, що мається на увазі під векторною проекцією одного вектора на інший вектор, і опишіть, як його обчислити.
- Розрахуйте виконану роботу за заданою силою.
Якщо ми докладаємо силу до об'єкта, щоб об'єкт рухався, ми говоримо, що робота виконується силою. Раніше ми дивилися на постійну силу і припускали, що сила прикладена в напрямку руху об'єкта. У цих умовах робота може виражатися як добуток сили, що діє на об'єкт, і відстані, на яку рухається об'єкт. Однак у цьому розділі ми бачили, що і сила, і рух об'єкта можуть бути представлені векторами.
У цьому розділі ми розробляємо операцію під назвою точковий добуток, яка дозволяє обчислити роботу в тому випадку, коли вектор сили і вектор руху мають різні напрямки. Точковий добуток по суті говорить нам, скільки вектора сили прикладено у напрямку вектора руху. Точковий добуток також може допомогти нам виміряти кут, утворений парою векторів, і положення вектора щодо осей координат. Він навіть забезпечує простий тест, щоб визначити, чи зустрічаються два вектори під прямим кутом.
Точковий добуток і його властивості
Ми вже навчилися складати і віднімати вектори. У цьому розділі ми досліджуємо два типи векторного множення. Перший тип векторного множення називається точковим добутком, виходячи з використовуваних нами для нього позначень, і визначається він наступним чином:
Точковий \(\vecs{ u}=⟨u_1,u_2,u_3⟩\)добуток векторів і\(\vecs{ v}=⟨v_1,v_2,v_3⟩\) задається сумою добутків складових
\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3. \nonumber \]
Зауважимо, що якщо\(u\) і\(v\) є двовимірними векторами, ми обчислюємо точковий добуток аналогічним чином. Таким чином, якщо\(\vecs{ u}=⟨u_1,u_2⟩\) і\(\vecs{ v}=⟨v_1,v_2⟩,\) тоді
\[\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2. \nonumber \]
Коли два вектори об'єднуються під додавання або віднімання, результатом є вектор. Коли два вектори об'єднані за допомогою крапкового добутку, результат є скалярним. З цієї причини крапковий добуток часто називають скалярним добутком. Його також можна назвати внутрішнім продуктом.
- Знайдіть точковий добуток\(\vecs{ u}=⟨3,5,2⟩\) і\(\vecs{ v}=⟨−1,3,0⟩\).
- Знайти скалярний добуток\(\vecs{ p}=10\hat{\textbf i}−4 \hat{\textbf j}+7 \hat{\textbf k}\) і\(\vecs{ q}=−2\hat{\textbf i}+\hat{\textbf j}+6\hat{\textbf k}.\)
Рішення:
а. підставити векторні компоненти у формулу крапкового добутку:
\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &=3(−1)+5(3)+2(0) \\[4pt] &=−3+15+0 \\[4pt] &=12. \end{align*}\]
б. розрахунок однаковий, якщо вектори записані за допомогою стандартних одиничних векторів. У нас ще є три компоненти для кожного вектора, які потрібно підставити у формулу крапкового добутку:
\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=p_1q_1+p_2q_2+p_3q_3 \\[4pt] &=10(−2)+(−4)(1)+(7)(6) \\[4pt] &=−20−4+42 \\[4pt] &=18.\end{align*}\]
Знайти\(\vecs{ u}⋅\vecs{ v}\), де\(\vecs{ u}=⟨2,9,−1⟩\) і\(\vecs{ v}=⟨−3,1,−4⟩.\)
- Підказка
-
Помножте відповідні компоненти, а потім додайте їх продукти.
- Відповідь
-
\(7\)
Як і векторне додавання і віднімання, крапковий добуток має кілька алгебраїчних властивостей. Доводимо три цих властивості, а решту залишаємо як вправи.
Дозволяти\(\vecs{ u}\)\(\vecs{ v}\), і\(\vecs{ w}\) бути вектори, і нехай\(c\) бути скалярним.
- Комутативне майно\[\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u} \nonumber \]
- Розподільна власність\[\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w} \nonumber \]
- Асоціативна властивість\[c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v}) \nonumber \]
- Властивість величини\[\vecs{ v}⋅\vecs{ v}=\|\vecs{ v}\|^2 \nonumber \]
Нехай\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) і\(\vecs{ v}=⟨v_1,v_2,v_3⟩.\) тоді
\[ \begin{align*} \vecs{ u}⋅\vecs{ v} &=⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=u_1v_1+u_2v_2+u_3v_3 \\[4pt] &= v_1u_1+v_2u_2+v_3u_3 \\[4pt] &= ⟨v_1,v_2,v_3⟩⋅⟨u_1,u_2,u_3⟩ \\[4pt] &=\vecs{ v}⋅\vecs{ u}.\end{align*}\]
Асоціативне властивість виглядає як асоціативна властивість для множення на дійсне число, але зверніть пильну увагу на різницю між скалярними і векторними об'єктами:
\[ \begin{align*} c(\vecs{ u}⋅\vecs{ v}) &=c(u_1v_1+u_2v_2+u_3v_3) \\[4pt] &=c(u_1v_1)+c(u_2v_2)+c(u_3v_3) \\[4pt] &=(cu_1)v_1+(cu_2)v_2+(cu_3)v_3 \\[4pt] &=⟨cu_1,cu_2,cu_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=c⟨u_1,u_2,u_3⟩⋅⟨v_1,v_2,v_3⟩ \\[4pt] &=(c\vecs{ u})⋅\vecs{ v}.\end{align*}\]
Доказ того,\(c(\vecs{ u}⋅\vecs{ v})=\vecs{ u}⋅(c\vecs{ v})\) що схоже.
Четверта властивість показує зв'язок між величиною вектора і його точковим добутком з самим собою:
\[ \begin{align*} \vecs{ v}⋅\vecs{ v} &=⟨v_1,v_2,v_3⟩⋅⟨v_1,v_2,v_3⟩\\[4pt] &=(v_1)^2+(v_2)^2+(v_3)^2 \\[4pt] &=\left[\sqrt{(v_1)^2+(v_2)^2+(v_3)^2}\right]^2 \\[4pt] &=\|\vecs{ v}\|^2.\end{align*}\]
□
Зверніть увагу, що визначення точкового добутку дає\(\vecs{ 0}⋅\vecs{ v}=0.\) За властивістю iv. якщо\(\vecs{ v}⋅\vecs{ v}=0,\) тоді\(\vecs{ v}=\vecs{ 0}.\)
Нехай\(\vecs{ a}=⟨1,2,−3⟩\),\(\vecs{ b}=⟨0,2,4⟩\), і\( \vecs{ c} =⟨5,−1,3⟩\).
Знайдіть кожен з наведених нижче продуктів.
- \(( \vecs{ a} ⋅ \vecs{ b}) \vecs{ c} \)
- \(\vecs{ a}⋅(2\vecs{ c})\)
- \(\|\vecs{ b}\|^2\)
Рішення
a Зауважте, що цей вираз запитує скалярне значення, кратне\(\vecs{ c}\) за\(\vecs{ a}⋅\vecs{ b}\):
\[ \begin{align*} (\vecs{ a}⋅\vecs{ b})\vecs{ c} &=(⟨1,2,−3⟩⋅⟨0,2,4⟩)⟨5,−1,3⟩ \\[4pt] &=(1(0)+2(2)+(−3)(4))⟨5,−1,3⟩ \\[4pt] &=−8⟨5,−1,3⟩ \\[4pt] &= ⟨−40,8,−24⟩.\end{align*}\]
б Цей вираз є точковим добутком вектора\(\vecs{ a}\) та скалярним кратним 2\(\vecs{ c}\):
\[ \begin{align*} \vecs{ a}⋅(2\vecs{ c}) &=2(\vecs{ a}⋅\vecs{ c}) \\[4pt] &=2(⟨1,2,−3⟩⋅⟨5,−1,3⟩) \\[4pt] &=2(1(5)+2(−1)+(−3)(3)) \\[4pt] &=2(−6)=−12.\end{align*}\]
c Спрощення цього виразу полягає в прямому застосуванні точкового добутку:
\[ \begin{align*} \|\vecs{ b}\|^2 &=\vecs{ b}⋅\vecs{ b} \\[4pt] &=⟨0,2,4⟩⋅⟨0,2,4⟩\\[4pt] &=0^2+2^2+4^2\\[4pt] &=0+4+16\\[4pt] &=20.\end{align*}\]
Знайдіть такі продукти для\(\vecs{ p}=⟨7,0,2⟩\)\(\vecs{ q}=⟨−2,2,−2⟩\), і\(\vecs{ r}=⟨0,2,−3⟩\).
- \((\vecs{ r}⋅\vecs{ p})\vecs{ q}\)
- \(\|\vecs{ p}\|^2\)
- Підказка
-
\(\vecs{ r}⋅\vecs{ p}\)є скаляром.
- Відповідь
-
\(a. \quad (\vecs{ r}⋅\vecs{ p})\vecs{ q}=⟨12,−12,12⟩; \quad b. \quad \|\vecs{ p}\|^2=53\)
Використання точкового добутку для пошуку кута між двома векторами
Коли два ненульових вектора розміщуються в стандартному положенні, будь то в двох вимірах або трьох вимірах, вони утворюють між ними кут (рис.\(\PageIndex{1}\)). Точковий добуток забезпечує спосіб знайти міру цього кута. Ця властивість є результатом того, що ми можемо висловити точковий добуток через косинус кута, утвореного двома векторами.
Точковий добуток двох векторів - добуток величини кожного вектора і косинуса кута між ними:
\[\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{evaldot} \]
Розмістіть вектори\(\vecs{ u}\) і\(\vecs{ v}\) в стандартному положенні і розгляньте вектор\(\vecs{ v}−\vecs{ u}\) (рис.\(\PageIndex{2}\)). Ці три вектори утворюють трикутник з довжиною сторін\(‖\vecs{ u}‖,‖\vecs{ v}‖\), і\(‖\vecs{ v}−\vecs{ u}‖\).
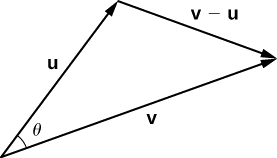
Нагадаємо з тригонометрії, що закон косинусів описує взаємозв'язок між довжинами сторін трикутника і кута\(θ\). Застосування закону косинусів тут дає
\[‖\vecs{ v}−\vecs{ u}‖^2=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \label{eq20} \]
Точковий добуток надає спосіб переписати ліву частину Equation\ ref {eq20}:
\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=(\vecs{ v}−\vecs{ u})⋅(\vecs{ v}−\vecs{ u}) \\[4pt] &=(\vecs{ v}−\vecs{ u})⋅\vecs{ v}−(\vecs{ v}−\vecs{ u})⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ v}⋅\vecs{ u}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=\vecs{ v}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}−\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ u} \\[4pt] &=‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2.\end{align*}\]
Підставляючи в закон косинусів прибутковості
\[ \begin{align*} ‖\vecs{ v}−\vecs{ u}‖^2 &=‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] ‖\vecs{ v}‖^2−2\vecs{ u}⋅\vecs{ v}+‖\vecs{ u}‖^2 &= ‖\vecs{ u}‖^2+‖\vecs{ v}‖^2−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] −2\vecs{ u}⋅\vecs{ v} &=−2‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] \vecs{ u}⋅\vecs{ v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ. \end{align*}\]
□
Ми можемо використовувати форму крапкового добутку в Equation\ ref {evaldot}, щоб знайти міру кута між двома ненульовими векторами шляхом перестановки рівняння\ ref {evaldot} для розв'язання косинуса кута:
\[\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}. \label{dot2} \]
Використовуючи це рівняння, ми можемо знайти косинус кута між двома ненульовими векторами. Оскільки ми розглядаємо найменший кут між векторами, ми припускаємо\(0°≤θ≤180°\) (або\(0≤θ≤π\) якщо ми працюємо в радіанах). Зворотний косинус є унікальним у цьому діапазоні, тому ми можемо визначити міру кута\(θ\).
Знайдіть міру кута між кожною парою векторів.
- \(\mathbf{\hat i} + \mathbf{\hat j} + \mathbf{\hat k}\)і\(2\mathbf{\hat i} – \mathbf{\hat j} – 3\mathbf{\hat k}\)
- \(⟨2,5,6⟩\)і\(⟨−2,−4,4⟩\)
Рішення
а Щоб знайти косинус кута, утвореного двома векторами, підставляємо компоненти векторів на Equation\ ref {dot2}:
\[ \begin{align*} \cos θ &=\dfrac{(\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k})⋅(2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k})}{∥\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}∥⋅∥2\mathbf{\hat i}−\mathbf{\hat j}−3\mathbf{\hat k}∥} \\[4pt] &=\dfrac{1(2)+(1)(−1)+(1)(−3)}{\sqrt{1^2+1^2+1^2}\sqrt{2^2+(−1)^2+(−3)^2}} \\[4pt] &=\dfrac{−2}{\sqrt{3}\sqrt{14}} =\dfrac{−2}{\sqrt{42}}. \end{align*}\]
Тому\(θ=\arccos\dfrac{−2}{\sqrt{42}}\) радий.
b. почніть з знаходження значення косинуса кута між векторами:
\[ \begin{align*} \cos θ &=\dfrac{⟨2,5,6⟩⋅⟨−2,−4,4⟩}{∥⟨2,5,6⟩∥⋅∥⟨−2,−4,4⟩∥} \\[4pt] &=\dfrac{2(−2)+(5)(−4)+(6)(4)}{\sqrt{2^2+5^2+6^2}\sqrt{(−2)^2+(−4)^2+4^2}} \\[4pt] &=\dfrac{0}{\sqrt{65}\sqrt{36}}=0.\end{align*}\]
Тепер,\(\cos θ=0\) і\(0≤θ≤π\), так\(θ=π/2\).
Знайти міру кута, в радіанах, утвореному векторами\(\vecs{ a}=⟨1,2,0⟩\) і\(\vecs{ b}=⟨2,4,1⟩\). Округлити до найближчої сотої.
- Підказка
-
Використовуйте рівняння\ ref {dot2}.
- Відповідь
-
\(θ≈0.22\)рад
Кут між двома векторами може бути гострим\((0<\cos θ<1),\) тупим\((−1<\cos θ<0)\), або прямим\((\cos θ=−1)\). Якщо\(\cos θ=1\), то обидва вектора мають однаковий напрямок. Якщо\(\cos θ=0\), то вектори при розміщенні в стандартному положенні утворюють прямий кут (рис.\(\PageIndex{3}\)). Ми можемо формалізувати цей результат у теорему щодо ортогональних (перпендикулярних) векторів.
Ненульові вектори\(\vecs{u}\) і\(\vecs{v}\) є ортогональними векторами, якщо і тільки тоді\(\vecs{u}⋅\vecs{v}=0.\)
\(\vecs{u}\)\(\vecs{v}\)Дозволяти і бути ненульові вектори, і нехай\(θ\) позначають кут між ними. Спочатку припустимо, що\(\vecs{u}⋅\vecs{v}=0.\) тоді
\[‖\vecs{u}‖‖\vecs{v}‖\cos θ=0. \nonumber \]
Втім,\(‖\vecs{u}‖≠0\) і\(‖\vecs{v}‖≠0,\) так ми повинні мати\(\cos θ=0\). Значить\(θ=90°\), і вектори ортогональні.
Тепер припустимо\(\vecs{u}\) і\(\vecs{v}\) є ортогональними. Тоді\(θ=90°\) і у нас
\[ \begin{align*} \vecs{u}⋅\vecs{v} &=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖\cos 90° \\[4pt] &=‖\vecs{ u}‖‖\vecs{ v}‖(0) \\[4pt] &=0. \end{align*}\]
□
Терміни ортогональний, перпендикулярний і нормальний кожен вказують на те, що математичні об'єкти перетинаються під прямим кутом. Вживання кожного терміна визначається головним чином його контекстом. Ми говоримо, що вектори ортогональні, а лінії перпендикулярні. Термін нормаль використовується найчастіше при вимірюванні кута, виконаного з площиною або іншою поверхнею.
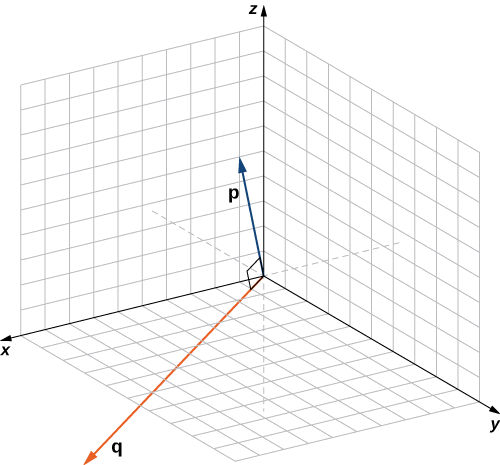
Визначте, чи\(\vecs{q}=⟨10,3,−2⟩\) є\(\vecs{p}=⟨1,0,5⟩\) і є ортогональними векторами.
Рішення
Використовуючи визначення, нам потрібно лише перевірити точковий добуток векторів:
\[ \vecs{ p}⋅\vecs{ q}=1(10)+(0)(3)+(5)(−2)=10+0−10=0. \nonumber \]
Тому\(\vecs{p}⋅\vecs{q}=0,\) що вектори ортогональні (рис.\(\PageIndex{4}\)).
Для якого значення з\(x\)\(\vecs{ p}=⟨2,8,−1⟩\) ортогонально\(\vecs{ q}=⟨x,−1,2⟩\)?
- Підказка
-
Вектори\(\vecs{ p}\) і\(\vecs{ q}\) є ортогональними, якщо і тільки якщо\(\vecs{ p}⋅\vecs{ q}=0\).
- Відповідь
-
\(x=5\)
Дозвольте\(\vecs{ v}=⟨2,3,3⟩.\) знайти міри кутів, утворених наступними векторами.
- \(\vecs{ v}\)і\(\mathbf{\hat i}\)
- \(\vecs{ v}\)і\(\mathbf{\hat j}\)
- \(\vecs{ v}\)і\(\mathbf{\hat k}\)
Рішення
a.Нехай α - кут, утворений\(\vecs{ v}\) і\(\mathbf{\hat i}\):
\[ \begin{align*} \cos{α} &=\dfrac{\vecs{ v}⋅\mathbf{\hat i}}{‖\vecs{ v}‖⋅\|\mathbf{\hat i}\|}=\dfrac{⟨2,3,3⟩⋅⟨1,0,0⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{2}{\sqrt{22}} \\[4pt] α &=\arccos\dfrac{2}{\sqrt{22}}≈1.130\,\text{rad.} \end{align*}\]
b. нехай β представляють кут, утворений\(\vecs{ v}\) і\(\mathbf{\hat j}\):
\[ \begin{align*} \cos{β} &=\dfrac{\vecs{ v}⋅\mathbf{\hat j}}{‖\vecs{ v}‖⋅\|\mathbf{\hat j}\|}=\dfrac{⟨2,3,3⟩⋅⟨0,1,0⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt] β &=\arccos\dfrac{3}{\sqrt{22}}≈0.877\,\text{rad.} \end{align*}\]
c Нехай γ представляють кут, утворений\(\vecs{ v}\) і\(\mathbf{\hat k}\):
\[ \begin{align*} \cos{γ} &=\dfrac{\vecs{ v}⋅\mathbf{\hat k}}{‖\vecs{ v}‖⋅\|\mathbf{\hat k}\|}=\dfrac{⟨2,3,3⟩⋅⟨0,0,1⟩}{\sqrt{2^2+3^2+3^2}\sqrt{1}}=\dfrac{3}{\sqrt{22}} \\[4pt]γ &=\arccos\dfrac{3}{\sqrt{22}}≈0.877\,\text{rad.} \end{align*}\]
Дозвольте\(\vecs{ v}=⟨3,−5,1⟩.\) знайти міру кутів, утворених кожною парою векторів.
- \(\vecs{ v}\)і\(\mathbf{\hat i}\)
- \(\vecs{ v}\)і\(\mathbf{\hat j}\)
- \(\vecs{ v}\)і\(\mathbf{\hat k}\)
- Підказка
-
\(\mathbf{\hat i}=⟨1,0,0⟩, \mathbf{\hat j}=⟨0,1,0⟩,\)і\(\mathbf{\hat k}=⟨0,0,1⟩\)
- Відповідь
-
\(a. α≈1.04\)рад; б.\(β≈2.58\) рад; с.\(γ≈1.40\) рад
Кут, який вектор робить з кожною з осей координат, званий кутом напряму, дуже важливий у практичних обчисленнях, особливо в такій галузі, як інженерія. Наприклад, в космонавтичній техніці кут, під яким запускається ракета, повинен бути визначений дуже точно. Дуже невелика похибка в куті може призвести до того, що ракета йде за сотні кілометрів від курсу. Кути напряму часто обчислюються за допомогою точкового добутку і косинусів кутів, званих косинусами напрямку. Тому ми визначаємо як ці кути, так і їх косинуси.
Кути, утворені ненульовим вектором і осями координат, називаються кутами напряму для вектора (рис.\(\PageIndex{5}\)). Косинуси для цих кутів називаються косинусами напрямку.
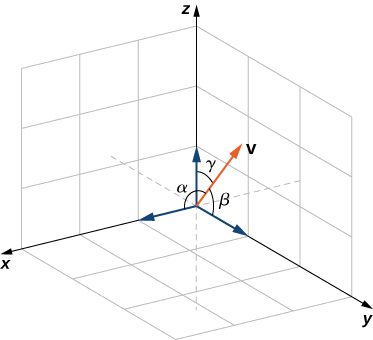
У\(\PageIndex{5}\) прикладі напрямки косинуси\(\vecs{ v}=⟨2,3,3⟩\) є\(\cos α=\dfrac{2}{\sqrt{22}}, \cos β=\dfrac{3}{\sqrt{22}},\) і\(\cos γ=\dfrac{3}{\sqrt{22}}\). Кути напряму\(\vecs{ v}\) є\(α=1.130\) rad,\(β=0.877\) rad і\(γ=0.877\) rad.
Поки що ми зосередилися переважно на векторах, пов'язаних із силою, рухом та положенням у тривимірному фізичному просторі. Однак вектори часто використовуються більш абстрактними способами. Наприклад, припустимо, що продавець фруктів продає яблука, банани та апельсини. У даний день він продає 30 яблук, 12 бананів і 18 апельсинів. Він може використовувати вектор кількості,\(\vecs{ q}=⟨30,12,18⟩,\) щоб представити кількість фруктів, які він продав того дня. Аналогічно, він може захотіти використовувати вектор цін,\(\vecs{ p}=⟨0.50,0.25,1⟩,\) щоб вказати, що він продає свої яблука по 50 центів кожен, банани по 25 центів кожен, а апельсини за $1 за штуку. У цьому прикладі, хоча ми все ще могли графувати ці вектори, ми не інтерпретуємо їх як буквальне уявлення про положення у фізичному світі. Ми просто використовуємо вектори, щоб відстежувати окремі фрагменти інформації про яблука, банани та апельсини.
Ця ідея може здатися трохи дивною, але якщо ми просто розглядаємо вектори як спосіб впорядкування та зберігання даних, ми виявимо, що вони можуть бути досить потужним інструментом. Повертаючись до продавця фруктів, давайте подумаємо про точковий продукт,\(\vecs{ q}⋅\vecs{ p}\). Ми обчислюємо це, множивши кількість проданих яблук (30) на ціну за яблуко (50 центів), кількість бананів, що продаються за ціною за банан, і кількість апельсинів, проданих за ціною апельсина. Потім ми додаємо всі ці значення разом. Отже, у цьому прикладі, точка продукт говорить нам, скільки грошей продавець фруктів мав у продажу в цей конкретний день.
Коли ми використовуємо вектори таким більш загальним способом, немає підстав обмежувати кількість компонентів трьома. Що робити, якщо продавець фруктів вирішить почати продавати грейпфрут? У цьому випадку він хотів би використовувати чотиривимірні вектори кількості та цін для представлення кількості проданих яблук, бананів, апельсинів та грейпфрутів та їх одиничних цін. Як і слід було очікувати, щоб обчислити точковий добуток чотиривимірних векторів, ми просто додаємо добуток компонентів, як і раніше, але сума має чотири члени замість трьох.
Магазин AAA Party Supply Store продає запрошення, вечірки, прикраси та предмети харчування, такі як паперові тарілки та серветки. Коли AAA купує свій інвентар, він платить 25 центів за пакет за запрошення та вечірки. Прикраси коштують AAA 50 центів кожен, а предмети харчування коштують 20 центів за упаковку. AAA продає запрошення за $2,50 за пакет, а партійні послуги за 1,50 долара за пакет. Прикраси продають за $4.50 кожен і продукти харчування за $1,25 за упаковку.
Протягом травня AAA Party Supply Store продає 1258 запрошень, 342 вечірки, 2426 прикрас та 1354 предметів громадського харчування. Використовуйте вектори і точкові продукти, щоб підрахувати, скільки грошей ААА зробив в продажах протягом травня місяця. Скільки заробив магазин прибутку?
Рішення
Вектори вартості, ціни та кількості
\[ \begin{align*} \vecs{ c} &=⟨0.25,0.25,0.50,0.20⟩ \\[4pt] \vecs{ p} &=⟨2.50,1.50,4.50,1.25⟩ \\[4pt] \vecs{ q} &=⟨1258,342,2426,1354⟩. \end{align*}\]
Продажі AAA за травень місяць можна розрахувати за допомогою точкового добутку\(\vecs{ p}⋅\vecs{ q}\). У нас є
\[ \begin{align*} \vecs{ p}⋅\vecs{ q} &=⟨2.50,1.50,4.50,1.25⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=3145+513+10917+1692.5 \\[4pt] &= 16267.5. \end{align*}\]
Так, ААА взяв $16 267.50 протягом травня місяця. Щоб розрахувати прибуток, ми повинні спочатку порахувати, скільки ААА заплатив за продані предмети. Використовуємо точковий добуток\(\vecs{c}⋅\vecs{q}\), щоб отримати
\[ \begin{align*} \vecs{ c}⋅\vecs{ q} &=⟨0.25,0.25,0.50,0.20⟩⋅⟨1258,342,2426,1354⟩ \\[4pt] &=314.5+85.5+1213+270.8 \\[4pt] &=1883.8. \end{align*}\]
Так, AAA заплатив $1,883,80 за продані ними предмети. Їх прибуток, значить, дається
\[\vecs{ p}⋅\vecs{ q}−\vecs{ c}⋅\vecs{ q}=16267.5−1883.8 =14383.7. \nonumber \]
Таким чином, AAA Party Supply Store склав $14,383.70 в травні.
1 червня AAA Party Supply Store вирішив збільшити ціну, яку вони стягують за партійні послуги, до 2 доларів за упаковку. Вони також змінили постачальників для своїх запрошень, і тепер можуть придбати запрошення лише за 10 центів за пакет. Всі інші їх витрати і ціни залишаються колишніми. Якщо AAA продає 1408 запрошень, 147 вечірок, 2112 прикрас та 1894 предметів громадського харчування в червні місяці, використовуйте вектори та точкові продукти, щоб обчислити їх загальний обсяг продажів та прибутку за червень.
- Підказка
-
Використовуйте чотиривимірні вектори для вартості, ціни та кількості проданих.
- Відповідь
-
Продажі = $15,685.50; прибуток = $14,073.15
Проекції
Як ми бачили, додавання об'єднує два вектори для створення результуючого вектора. Але що робити, якщо нам дано вектор і нам потрібно знайти його складові частини? Ми використовуємо векторні проекції для виконання протилежного процесу; вони можуть розбити вектор на його складові. Величина векторної проекції - це скалярна проекція. Наприклад, якщо дитина тягне за ручку вагона під кутом 55°, ми можемо використовувати проекції, щоб визначити, скільки сили на рукоятці насправді рухає вагон вперед (\(\PageIndex{6}\)). Повертаємося до цього прикладу і дізнаємося, як його вирішувати після того, як побачимо, як обчислювати прогнози.
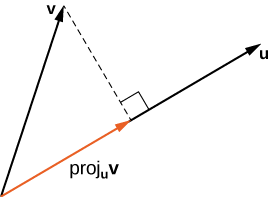
Векторна проекція\(\vecs{ v}\) onto\(\vecs{ u}\) - це вектор, позначений\(\text{proj}_\vecs{ u}\vecs{ v}\) на малюнку\(\PageIndex{7}\). Він має ту саму початкову точку\(\vecs{ u}\), як\(\vecs{ u}\)\(\vecs{ v}\) і в тому ж напрямку, і являє собою компонент\(\vecs{ v}\), який діє в напрямку\(\vecs{ u}\). Якщо\(θ\) представляє кут між\(\vecs{ u}\) і\(\vecs{ v}\), то, за властивостями трикутників, ми знаємо довжину\(\text{proj}_\vecs{ u}\vecs{ v}\) є\(\|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs{ v}‖\cos θ.\) При вираженні\(\cos θ\) в терміні точкового добутку, це стає
\[ \|\text{proj}_\vecs{ u}\vecs{ v}\|=‖\vecs v‖\cos θ=‖\vecs{ v}‖\left(\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.} \nonumber \]
Тепер множимо на одиничний вектор у напрямку,\(\vecs{ u}\) щоб отримати\(\text{proj}_\vecs{ u}\vecs{ v}\):
\[\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\left(\dfrac{1}{‖\vecs{ u}‖}\vecs{ u}\right)=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}. \nonumber \]
Довжина цього вектора також відома як скалярна\(\vecs{ v}\) проекція на\(\vecs{ u}\) і позначається
\[\|\text{proj}_\vecs{ u}\vecs{ v}\|=\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖.} \nonumber \]
Знайдіть проекцію\(\vecs{ v}\) на\(\vecs{ u}\).
- \(\vecs{v}=⟨3,5,1⟩\)і\(\vecs{u}=⟨−1,4,3⟩\)
- \(\vecs{v}=3\mathbf{\hat i}−2\mathbf{\hat j}\)і\(\vecs{u}=\mathbf{\hat i}+6\mathbf{\hat j}\)
Рішення
а. підставляємо компоненти\(\vecs{ v}\) і\(\vecs{ u}\) в формулу проекції:
\[\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨−1,4,3⟩⋅⟨3,5,1⟩}{∥⟨−1,4,3⟩∥^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{−3+20+3}{(−1)^2+4^2+3^2}⟨−1,4,3⟩ \\[4pt] &=\dfrac{20}{26}⟨−1,4,3⟩ \\[4pt] &=⟨−\dfrac{10}{13},\dfrac{40}{13},\dfrac{30}{13}⟩. \end{align*}\]
б. щоб знайти двомірну проекцію, досить просто адаптувати формулу до двовимірного випадку:
\[\begin{align*} \text{proj}_\vecs{ u}\vecs{ v} &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{(\mathbf{\hat i}+6\mathbf{\hat j})⋅(3\mathbf{\hat i}−2\mathbf{\hat j})}{∥\mathbf{\hat i}+6\mathbf{\hat j}∥^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= \dfrac{1(3)+6(−2)}{1^2+6^2}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= −\dfrac{9}{37}(\mathbf{\hat i}+6\mathbf{\hat j}) \\[4pt] &= −\dfrac{9}{37}\mathbf{\hat i}−\dfrac{54}{37}\mathbf{\hat j}.\end{align*}\]
Іноді корисно розкласти вектори, тобто розбити вектор на суму. Цей процес називається роздільною здатністю вектора на складові. Проекції дозволяють виділити два ортогональних вектора, що мають бажану суму. Наприклад, нехай\(\vecs{ v}=⟨6,−4⟩\) і нехай\(\vecs{ u}=⟨3,1⟩.\) Ми хочемо, щоб\(\vecs{ v}\) розкласти вектор на ортогональні компоненти таким чином, що один з векторів компонентів має той же напрямок, що і\(\vecs{ u}\).
Спочатку ми знаходимо компонент, який має той же напрямок, що і\(\vecs{ u}\) проектуючи\(\vecs{ v}\) на\(\vecs{ u}\). Нехай\(\vecs{ p}=\text{proj}_\vecs{ u}\vecs{ v}\). Тоді у нас є
\[\begin{align*}\vecs{ p} =\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] = \dfrac{18−4}{9+1}\vecs{ u} \\[4pt] = \dfrac{7}{5}\vecs{ u}=\dfrac{7}{5}⟨3,1⟩=⟨\dfrac{21}{5},\dfrac{7}{5}⟩. \end{align*}\]
Тепер розглянемо вектор У\(\vecs{ q}=\vecs{ v}−\vecs{ p}.\) нас є
\[\begin{align*} \vecs{ q} =\vecs{ v}−\vecs{ p} \\[4pt] = ⟨6,−4⟩−⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[4pt] = ⟨\dfrac{9}{5},−\dfrac{27}{5}⟩. \end{align*}\]
Зрозуміло, що за тим, як ми визначили\(\vecs{ q}\), ми маємо\(\vecs{ v}=\vecs{ q}+\vecs{ p},\) і
\[\begin{align*}\vecs{ q}⋅\vecs{ p} =⟨\dfrac{9}{5},−\dfrac{27}{5}⟩⋅⟨\dfrac{21}{5},\dfrac{7}{5}⟩ \\[4pt] = \dfrac{9(21)}{25}+−\dfrac{27(7)}{25} \\[4pt] = \dfrac{189}{25}−\dfrac{189}{25}=0. \end{align*}\]
Тому\(\vecs{ q}\) і\(\vecs{ p}\) бувають ортогональними.
\(\vecs{ v}=⟨8,−3,−3⟩\)Висловіть як суму ортогональних векторів таким чином, що один з векторів має такий же напрямок, як\(\vecs{ u}=⟨2,3,2⟩.\)
Рішення
\(\vecs{ p}\)Дозволяти представляти проекцію\(\vecs{ v}\) на\(\vecs{ u}\):
\[ \begin{align*} \vecs{ p} &=\text{proj}_\vecs{ u}\vecs{ v} \\[4pt] &=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u} \\[4pt] &=\dfrac{⟨2,3,2⟩⋅⟨8,−3,−3⟩}{∥⟨2,3,2⟩∥^2}⟨2,3,2⟩ \\[4pt] &=\dfrac{16−9−6}{2^2+3^2+2^2}⟨2,3,2⟩ \\[4pt] &=\dfrac{1}{17}⟨2,3,2⟩ \\[4pt] &=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩. \end{align*} \nonumber \]
Потім,
\[ \begin{align*} \vecs{ q} &=\vecs{ v}−\vecs{ p}=⟨8,−3,−3⟩−⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩\\[4pt] &=⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩. \end{align*} \nonumber \]
Щоб перевірити нашу роботу, ми можемо використовувати точковий добуток, щоб перевірити, що\(\vecs{ p}\) і\(\vecs{ q}\) є ортогональними векторами:
\[ \begin{align*}\vecs{ p}⋅\vecs{ q}&=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩⋅⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩\\[4pt] &=\dfrac{268}{289}−\dfrac{162}{289}−\dfrac{106}{289}=0. \end{align*} \nonumber \]
Потім,
\[\vecs{ v}=\vecs{ p}+\vecs{ q}=⟨\dfrac{2}{17},\dfrac{3}{17},\dfrac{2}{17}⟩+⟨\dfrac{134}{17},−\dfrac{54}{17},−\dfrac{53}{17}⟩. \nonumber \]
\(\vecs{ v}=5\mathbf{\hat i}−\mathbf{\hat j}\)Висловіть як суму ортогональних векторів таким чином, щоб один з векторів мав той же напрямок, що і\(\vecs{ u}=4\mathbf{\hat i}+2\mathbf{\hat j}\).
- Підказка
-
Почніть з пошуку проекції\(\vecs{ v}\) на\(\vecs{ u}\).
- Відповідь
-
\(\vecs{ v}=\vecs{ p}+\vecs{ q},\)де\(\vecs{ p}=\dfrac{18}{5}\mathbf{\hat i}+\dfrac{9}{5}\mathbf{\hat j}\) і\(\vecs{ q}=\dfrac{7}{5}\mathbf{\hat i}−\dfrac{14}{5}\mathbf{\hat j}\)
Контейнеровоз залишає порт подорожі на\(15°\) північ від сходу. Його двигун генерує швидкість 20 вузлів по цьому шляху (див. Наступний малюнок). Крім того, океанічна течія рухає корабель на північний схід зі швидкістю 2 вузли. Враховуючи і двигун, і течію, наскільки швидко рухається корабель в напрямку на\(15°\) північ від сходу? Округляйте відповідь до двох знаків після коми.
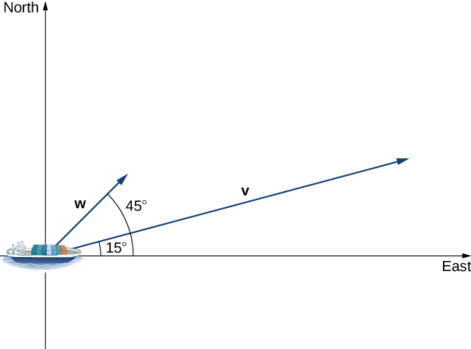
Рішення
\(\vecs{ v}\)Дозволяти вектор швидкості, що генерується двигуном, і\(\vecs{w}\) нехай вектор швидкості струму. Ми вже знаємо\(‖\vecs{ v}‖=20\) по бажаному маршруту. Нам просто потрібно додати в скалярній проекції\(\vecs{ w}\) на\(\vecs{ v}\). Ми отримуємо
\[ \begin{align*} \text{comp}_\vecs{ v}\vecs{ w}=\dfrac{\vecs{ v}⋅\vecs{ w}}{‖\vecs{ v}‖} \\[4pt] =\dfrac{‖\vecs{ v}‖‖\vecs{ w}‖\cos(30°)}{‖\vecs{ v}‖} =‖\vecs{ w}‖\cos(30°) =2\dfrac{\sqrt{3}}{2}=\sqrt{3}≈1.73\,\text{knots.}\end{align*}\]
Судно рухається на рівні 21,73 вузла в напрямку на\(15°\) північ від сходу.
Повторіть попередній приклад, але припустимо, що океанська течія рухається на південний схід замість північного сходу, як показано на наступному малюнку.
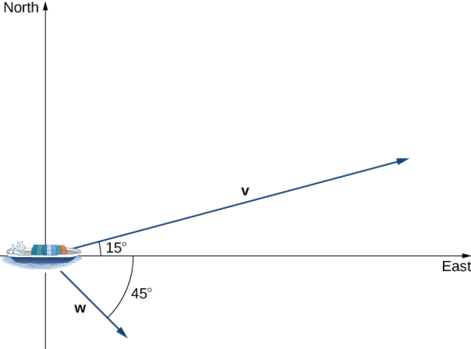
- Підказка
-
Обчислити скалярну проекцію\(\vecs{ w}\) onto\(\vecs{ v}\).
- Відповідь
-
21 вузлів
Робота
Тепер, коли ми розуміємо точкові продукти, ми можемо побачити, як застосовувати їх до реальних життєвих ситуацій. Найбільш поширене застосування точкового добутку двох векторів - при обчисленні роботи.
З фізики ми знаємо, що робота виконується, коли об'єкт переміщується силою. Коли сила постійна і прикладена в тому ж напрямку, в якому рухається об'єкт, то ми визначаємо виконану роботу як добуток сили і відстань, яку проходить об'єкт:\(W=Fd\). Ми бачили кілька прикладів такого типу в попередніх розділах. Тепер уявіть, що напрямок сили відрізняється від напрямку руху, як на прикладі дитини, що тягне за собою візок. Щоб знайти виконану роботу, нам потрібно помножити складову сили, яка діє в напрямку руху, на величину зміщення. Точковий продукт дозволяє нам робити саме це. Якщо уявити прикладену силу вектором\(\vecs{ F}\) і зміщення предмета вектором\(\vecs{ s}\), то робота, виконана силою, є точковим добутком\(\vecs{ F}\) і\(\vecs{ s}\).
Коли постійна сила прикладається до об'єкта таким чином, об'єкт рухається по прямій лінії від точки\(P\) до точки\(Q\), робота,\(W\) виконана силою\(\vecs{ F}\), діючи під кутом θ від лінії руху, задається
\[W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ. \nonumber \]
Давайте повернемося до проблеми дитячої візок, введеної раніше. Припустимо, дитина тягне вагон із силою, що має величину 8 фунтів на ручці під кутом 55°. Якщо дитина тягне візок 50 футів, знайдіть виконану роботу силою (рис.\(\PageIndex{8}\)).
У нас є
\[W=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ=8(50)(\cos(55°))≈229\,\text{ft⋅lb.} \nonumber \]
У стандартних одиницях США ми вимірюємо величину сили\(∥\vecs{ F}∥\) в фунтах. Величина вектора зміщення\(∥\vecd{PQ}∥\) говорить нам про те, наскільки далеко перемістився об'єкт, і він вимірюється в футах. Звичайною одиницею виміру для роботи, значить, є фут-фунт. Один фут-фунт - це обсяг роботи, необхідний для переміщення об'єкта вагою 1 фунт на відстань 1 фут прямо вгору. У метричній системі одиницею виміру сили є ньютон (N), а одиницею виміру величини для роботи є ньютон-метр (N·m), або джоуль (J).
Конвеєрна стрічка генерує силу\(\vecs{ F}=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}\), яка переміщує валізу з точки\((1,1,1)\) в точку\((9,4,7)\) вздовж прямої лінії. Знайти роботу, виконану стрічкою конвеєра. Відстань вимірюється в метрах, а сила вимірюється в ньютонах.
Рішення
Вектор зміщення\(\vecd{PQ}\) має початкову точку\((1,1,1)\) та кінцеву точку\((9,4,7)\):
\[\vecd{PQ}=⟨9−1,4−1,7−1⟩=⟨8,3,6⟩=8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}. \nonumber \]
Робота є точковим добутком сили і зміщення:
\[\begin{align*} W &=\vecs{ F}⋅\vecd{PQ} \\[4pt] &= (5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k})⋅(8\mathbf{\hat i}+3\mathbf{\hat j}+6\mathbf{\hat k}) \\[4pt] = 5(8)+(−3)(3)+1(6) \\[4pt] &=37\,\text{N⋅m} \\[4pt] &= 37\,\text{J} \end{align*}\]
Постійна сила 30 фунтів застосовується під кутом 60°, щоб тягнути ручну візок 10 футів по землі. Яка робота виконується цією силою?
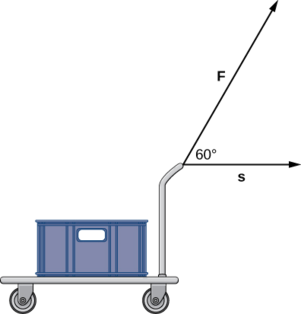
- Підказка
-
Використовуйте визначення роботи як точковий добуток сили і відстані.
- Відповідь
-
150 фут-фунт
Ключові концепції
- Точковий добуток, або скалярний добуток, двох векторів\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) і\(\vecs{ v}=⟨v_1,v_2,v_3⟩\) є\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\).
- Точковий добуток задовольняє наступним властивостям:
- \(\vecs{ u}⋅\vecs{ v}=\vecs{ v}⋅\vecs{ u}\)
- \(\vecs{ u}⋅(\vecs{ v}+\vecs{ w})=\vecs{ u}⋅\vecs{ v}+\vecs{ u}⋅\vecs{ w}\)
- \(c(\vecs{ u}⋅\vecs{ v})=(c\vecs{ u})⋅\vecs{ v}=\vecs{ u}⋅(c\vecs{ v})\)
- \(\vecs{ v}⋅\vecs{ v}=‖\vecs{ v}‖^2\)
- Точковий добуток двох векторів може бути виражений альтернативно, оскільки\(\vecs{ u}⋅\vecs{ v}=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ.\) Ця форма крапкового добутку корисна для знаходження міри кута, утвореного двома векторами.
- Вектори\(\vecs{ u}\) і\(\vecs{ v}\) є ортогональними, якщо\(\vecs{ u}⋅\vecs{ v}=0\).
- Кути, утворені ненульовим вектором і осями координат, називаються кутами напряму для вектора. Косинуси цих кутів відомі як косинуси напрямку.
- Векторна проекція\(\vecs{ v}\) onto\(\vecs{ u}\) - це вектор\(\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\). Величина цього вектора відома як скалярна проекція\(\vecs{ v}\) onto\(\vecs{ u}\), задана\(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\).
- Робота проводиться при прикладанні сили до об'єкта, що викликає зміщення. Коли сила представлена вектором,\(\vecs{ F}\) а зміщення представлено вектором\(\vecs{ s}\), то виконана робота\(W\) задається формулою\(W=\vecs{ F}⋅\vecs{ s}=∥\vecs{ F}∥‖\vecs{ s}‖\cos θ.\)
Ключові рівняння
- Точковий добуток\(\vecs{ u}\) і\(\vecs{ v}\)
\(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3=‖\vecs{ u}‖‖\vecs{ v}‖\cos θ\)
- Косинус кута, утвореного\(\vecs{ u}\) і\(\vecs{ v}\)
\(\cos θ=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖‖\vecs{ v}‖}\)
- Векторна проекція\(\vecs{ v}\) на\(\vecs{ u}\)
\(\text{proj}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖^2}\vecs{ u}\)
- Скалярна проекція\(\vecs{ v}\) на\(\vecs{ u}\)
\(\text{comp}_\vecs{ u}\vecs{ v}=\dfrac{\vecs{ u}⋅\vecs{ v}}{‖\vecs{ u}‖}\)
- Робота, виконана\(\vecs{ F}\) силою для переміщення об'єкта через вектор переміщення\(\vecd{PQ}\)
\(W=\vecs{ F}⋅\vecd{PQ}=∥\vecs{ F}∥∥\vecd{PQ}∥\cos θ\)
Глосарій
- кути напряму
- кути, утворені ненульовим вектором і осями координат
- косинуси напряму
- косинуси кутів, утворених ненульовим вектором і координатними осями
- точковий добуток або скалярний добуток
- \(\vecs{ u}⋅\vecs{ v}=u_1v_1+u_2v_2+u_3v_3\)де\(\vecs{ u}=⟨u_1,u_2,u_3⟩\) і\(\vecs{ v}=⟨v_1,v_2,v_3⟩\)
- скалярна проекція
- величина векторної проекції вектора
- ортогональні вектори
- вектори, які утворюють прямий кут при розміщенні в стандартному положенні
- векторна проекція
- компонент вектора, який слідує заданому напрямку
- робота, виконана силою
- робота, як правило, розглядається як кількість енергії, необхідної для переміщення об'єкта; якщо ми представляємо прикладену силу вектором\(\vecs{ F}\) і зміщення об'єкта на вектор\(\vecs{ s}\), то робота, виконана силою, є точковим добутком\(\vecs{ F}\) і\(\vecs{ s}\).
Дописувачі та атрибуція
- Template:ContribOpenStaxCalc
- edited for vector notation by Paul Seeburger
