4.6: Параметричні лінії
- Page ID
- 63099
- Знайти векторні та параметричні рівняння прямої.
Ми можемо використовувати концепцію векторів і точок, щоб знайти рівняння для довільних ліній в\(\mathbb{R}^n\), хоча в цьому розділі фокус буде на рядках в\(\mathbb{R}^3\).
Для початку розглянемо випадок\(n=1\) так у нас\(\mathbb{R}^{1}=\mathbb{R}\). Тут є лише один рядок, який є звичним числовим рядком, тобто\(\mathbb{R}\) сама по собі. Тому не варто досліджувати випадок\(n=1\) далі.
Тепер розглянемо випадок\(n=2\), коли, іншими словами\(\mathbb{R}^2\). \(P\)\(P_0\)Дозволяти і бути дві різні точки\(\mathbb{R}^{2}\), в яких містяться в рядку\(L\). \(\vec{p}\)\(\vec{p_0}\)Дозволяти і бути вектори положення для точок\(P\) і\(P_0\) відповідно. Припустимо, що\(Q\) це довільна точка на\(L\). Розглянемо наступну схему.
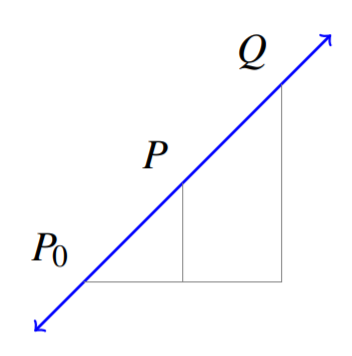
Наша мета - вміти визначати з\(Q\) точки зору\(P\) і\(P_0\). Розглянемо вектор\(\overrightarrow{P_0P} = \vec{p} - \vec{p_0}\), у якого є хвіст\(P_0\) і точка на\(P\). Якщо ми додамо\(\vec{p} - \vec{p_0}\) до вектора позиції\(\vec{p_0}\) для\(P_0\), сума буде вектором з його точкою в\(P\). Іншими словами,\[\vec{p} = \vec{p_0} + (\vec{p} - \vec{p_0})\nonumber \]
Тепер припустимо, що ми повинні були додати\(t(\vec{p} - \vec{p_0})\) до\(\vec{p}\) де\(t\) є деякі скалярні. Ви можете бачити, що, зробивши це, ми могли б знайти вектор з його точкою в\(Q\). Іншими словами, ми можемо знайти\(t\) таке, що\[\vec{q} = \vec{p_0} + t \left( \vec{p}- \vec{p_0}\right)\nonumber \]
Це рівняння визначає рядок\(L\) в\(\mathbb{R}^2\). По суті, він визначає рядок\(L\) в\(\mathbb{R}^n\). Розглянемо наступне визначення.
Припустимо\(L\), рядок\(\mathbb{R}^{n}\) містить дві різні точки\(P\) і\(P_0\). \(\vec{p}\)\(\vec{p_0}\)Дозволяти і бути вектори положення цих двох точок, відповідно. Потім,\(L\) це набір точок,\(Q\) які мають вектор позиції,\(\vec{q}\) заданий\[\vec{q}=\vec{p_0}+t\left( \vec{p}-\vec{p_0}\right)\nonumber \] де\(t\in \mathbb{R}\).
Нехай\(\vec{d} = \vec{p} - \vec{p_0}\). Потім\(\vec{d}\) - вектор напрямку для,\(L\) а векторне рівняння для\(L\) задається\[\vec{p}=\vec{p_0}+t\vec{d}, t\in\mathbb{R}\nonumber \]
Зверніть увагу, що це визначення узгоджується зі звичайним поняттям лінії в двох вимірах і тому це узгоджується з більш ранніми поняттями. Розглянемо тепер пункти в\(\mathbb{R}^3\). Якщо точка\(P \in \mathbb{R}^3\) задається\(P = \left( x,y,z \right)\),\(P_0 \in \mathbb{R}^3\) по\(P_0 = \left( x_0, y_0, z_0 \right)\), то ми можемо написати\[\left[ \begin{array}{c} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{c} x_0 \\ y_0 \\ z_0 \end{array} \right] + t \left[ \begin{array}{c} a \\ b \\ c \end{array} \right] \nonumber \] де\(\vec{d} = \left[ \begin{array}{c} a \\ b \\ c \end{array} \right]\). Це векторне рівняння,\(L\) записане в складовій формі.
Наступна теорема стверджує, що таке рівняння насправді є лінією.
Нехай\(\vec{a},\vec{b}\in \mathbb{R}^{n}\) с\(\vec{b}\neq \vec{0}\). Потім\(\vec{x}=\vec{a}+t\vec{b},\; t\in \mathbb{R}\), це лінія.
- Доказ
-
Нехай\(\vec{x_{1}}, \vec{x_{2}} \in \mathbb{R}^n\). Визначте\(\vec{x_{1}}=\vec{a}\) і нехай\(\vec{x_{2}}-\vec{x_{1}}=\vec{b}\). Так як\(\vec{b} \neq \vec{0}\), випливає, що\(\vec{x_{2}}\neq \vec{x_{1}}.\) Тоді\(\vec{a}+t\vec{b}=\vec{x_{1}} + t\left( \vec{x_{2}}-\vec{x_{1}}\right)\). Звідси випливає, що\(\vec{x}=\vec{a}+t\vec{b}\) це рядок, що містить дві різні точки\(X_1\) і вектори положення\(X_2\) якої задаються\(\vec{x}_2\) відповідно\(\vec{x}_1\) і.
Ми можемо використовувати вищезазначене обговорення, щоб знайти рівняння прямої, коли задано дві різні точки. Розглянемо наступний приклад.
Знайти векторне рівняння для прямої через точки\(P_0 = \left( 1,2,0\right)\) і\(P = \left( 2,-4,6\right).\)
Рішення
Ми будемо використовувати визначення рядка, наведеного вище в Definition, \(\PageIndex{1}\)щоб записати цей рядок у вигляді
\[\vec{q}=\vec{p_0}+t\left( \vec{p}-\vec{p_0}\right)\nonumber \]
Нехай\(\vec{q} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]B\). Потім ми можемо знайти\(\vec{p}\) і\(\vec{p_0}\) взявши вектори положення точок\(P\) і\(P_0\) відповідно. Потім,
\[\vec{q}=\vec{p_0}+t\left( \vec{p}-\vec{p_0}\right)\nonumber \]можна записати як
\[\left[ \begin{array}{c} x \\ y \\ z \\ \end{array} \right]B = \left[ \begin{array}{c} 1 \\ 2 \\ 0 \end{array} \right]B + t \left[ \begin{array}{r} 1 \\ -6 \\ 6 \end{array} \right]B, \;t\in \mathbb{R}\nonumber \]
Тут вектор напрямку\(\left[ \begin{array}{r} 1 \\ -6 \\ 6 \end{array} \right]B\) отримується так,\(\vec{p} - \vec{p_0} = \left[ \begin{array}{r} 2 \\ -4 \\ 6 \end{array} \right]B - \left[ \begin{array}{r} 1 \\ 2 \\ 0 \end{array} \right]B\) як зазначено вище у Визначенні\(\PageIndex{1}\).
Зверніть увагу, що в наведеному вище прикладі ми сказали, що ми знайшли «a» векторне рівняння для прямої, а не «рівняння». Причина цієї термінології полягає в тому, що існує нескінченно багато різних векторних рівнянь для однієї лінії. Щоб побачити це, замініть\(t\) іншим параметром, скажімо\(3s.\) Тоді ви отримаєте інше векторне рівняння для тієї ж лінії, оскільки виходить однаковий набір точок.
У прикладі вектор\(\PageIndex{1}\), заданий,\(\left[ \begin{array}{r} 1 \\ -6 \\ 6 \end{array} \right]B\) є вектора напрямку, визначеного в Definition\(\PageIndex{1}\). Якщо ми знаємо вектор напрямку прямої, а також точку на прямій, ми можемо знайти векторне рівняння.
Розглянемо наступний приклад.
Знайти векторне рівняння для прямої, яка містить точку\(P_0 = \left( 1,2,0\right)\) та має вектор напрямку\(\vec{d} = \left[ \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right]B\)
Рішення
Ми будемо використовувати Definition,\(\PageIndex{1}\) щоб записати цей рядок у формі\(\vec{p}=\vec{p_0}+t\vec{d},\; t\in \mathbb{R}\). Нам дано вектор напрямку\(\vec{d}\). Для того\(\vec{p_0}\), щоб знайти, ми можемо використовувати вектор положення точки\(P_0\). Це задається\(\left[ \begin{array}{c} 1 \\ 2 \\ 0 \end{array} \right]B.\)\(\vec{p} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]B\) Letting, рівняння для прямої задається\[\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]B = \left[ \begin{array}{c} 1 \\ 2 \\ 0 \end{array} \right]B + t \left[ \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right]B, \;t\in \mathbb{R} \label{vectoreqn}\]
Іноді ми обираємо написати такий рядок, як той, який наведено\(\eqref{vectoreqn}\) у вигляді\[\begin{array}{ll} \left. \begin{array}{l} x=1+t \\ y=2+2t \\ z=t \end{array} \right\} & \mbox{where} \; t\in \mathbb{R} \end{array} \label{parameqn}\] Цей набір рівнянь дає ту ж інформацію\(\eqref{vectoreqn}\), що і називається параметричним рівнянням прямої.
Розглянемо наступне визначення.
\(L\)Дозволяти лінія\(\mathbb{R}^3\), в якій має напрямок вектор\(\vec{d} = \left[ \begin{array}{c} a \\ b \\ c \end{array} \right]B\) і проходить через точку\(P_0 = \left( x_0, y_0, z_0 \right)\). Потім, дозволяючи\(t\) бути параметром, ми можемо записати\(L\) як\[\begin{array}{ll} \left. \begin{array}{c} x = x_0 + ta \\ y = y_0 + tb \\ z = z_0 + tc \end{array} \right\} & \mbox{where} \; t\in \mathbb{R} \end{array}\nonumber \] Це називається параметричне рівняння рядка\(L\).
Ви можете переконатися, що форма, розглянута нижче Приклад\(\PageIndex{2}\) у рівнянні\(\eqref{parameqn}\), має форму, наведену у Визначенні\(\PageIndex{2}\).
Існує ще одна форма для рядка, яка є корисною, яка є симетричною формою. Розглянемо рядок, задану\(\eqref{parameqn}\). Ви можете вирішити для параметра\(t\) записати\[\begin{array}{l} t=x-1 \\ t=\frac{y-2}{2} \\ t=z \end{array}\nonumber \] Тому,\[x-1=\frac{y-2}{2}=z\nonumber \] Це симетрична форма рядка.
У наступному прикладі ми розглянемо, як прийняти рівняння прямої від симетричної форми до параметричної форми.
Припустимо, симетричною формою рядка є\[\frac{x-2}{3}=\frac{y-1}{2}=z+3\nonumber \] Запишіть рядок у параметричній формі, а також у векторній формі.
Рішення
Ми хочемо написати цей рядок у формі, заданій Definition\(\PageIndex{2}\). Це форми\[\begin{array}{ll} \left. \begin{array}{c} x = x_0 + ta \\ y = y_0 + tb \\ z = z_0 + tc \end{array} \right\} & \mbox{where} \; t\in \mathbb{R} \end{array}\nonumber \]
Нехай\(t=\frac{x-2}{3},t=\frac{y-1}{2}\) і\(t=z+3\), як дано в симетричній формі лінії. Потім рішення для\(x,y,z,\) врожайності\[\begin{array}{ll} \left. \begin{array}{c} x=2 + 3t \\ y=1 + 2t \\ z=-3 + t \end{array} \right\} & \mbox{with} \;t\in \mathbb{R} \end{array}\nonumber \]
Це параметричне рівняння для цієї лінії.
Тепер, ми хочемо, щоб написати цей рядок у формі, заданої Definition\(\PageIndex{1}\). Це форма\[\vec{p}=\vec{p_0}+t\vec{d}\nonumber\] де\(t\in \mathbb{R}\). Це рівняння стає\[\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]B = \left[ \begin{array}{r} 2 \\ 1 \\ -3 \end{array} \right]B + t \left[ \begin{array}{r} 3 \\ 2 \\ 1 \end{array} \right]B, \;t\in \mathbb{R}\nonumber \]
