3.4: Властивості детермінанта

Цілі навчання

• Вибір для обчислення визначника матриці за допомогою розширення кофактора вздовж будь-якого рядка або стовпця є найбільш корисним, коли є багато того, що в рядку або стовпці?
• Яка елементарна операція рядка не змінює детермінант матриці?
• Чому математики рідко посміхаються?
• T/F: Коли комп'ютери використовуються для обчислення визначника матриці, кофакторне розширення використовується рідко.

У попередньому розділі ми дізналися, як обчислити детермінант. У цьому розділі ми дізнаємося деякі властивості детермінанти, і це дозволить нам легше обчислити детермінанти. У наступному розділі ми побачимо одне застосування детермінант.

Почнемо з теореми, яка дає нам більше свободи при обчисленні детермінант.

Теорема\(\PageIndex{1}\)

Розширення кофактора вздовж будь-якого рядка або стовпця

\(A\)Дозволяти бути\(n\times n\) матрицею. Визначник\(A\) може бути обчислений за допомогою кофакторного розширення уздовж будь-якого рядка або стовпця\(A\).

Ми посилалися на цей факт шлях назад після Приклад 3.3.3. Ми щойно дізналися, що таке розширення кофактора, і ми практикували уздовж другого ряду і вниз по третьому стовпчику. Пізніше ми знайшли детермінант цієї матриці шляхом обчислення кофакторного розширення уздовж першого ряду. У всіх трьох випадках ми отримали номер\(0\). Це не було випадковістю. Вищезазначена теорема стверджує, що всі три розширення фактично обчислювали детермінант.

Як це нам допомагає? Надаючи нам свободу вибору будь-якого рядка або стовпця для розширення, ми можемо вибрати рядок або стовпець, який виглядає «найбільш привабливим». Зазвичай це означає «у нього багато нулів». Цей принцип ми демонструємо нижче.

Приклад\(\PageIndex{1}\)

Знайдіть детермінант

\[A=\left[\begin{array}{cccc}{1}&{2}&{0}&{9}\\{2}&{-3}&{0}&{5}\\{7}&{2}&{3}&{8}\\{-4}&{1}&{0}&{2}\end{array}\right]. \nonumber \]

Рішення

Наша перша реакція цілком може бути «О ні! Не інший\(4\times 4\) детермінант!» Однак ми можемо використовувати розширення кофактора вздовж будь-якого рядка або стовпця, який ми вибираємо. Третій стовпець виглядає чудово; в ньому багато нулів. Розширення кофактора уздовж цієї колонки дорівнює\[\begin{align}\begin{aligned} \text{det}(A) & = a_{1,3}C_{1,3} + a_{2,3}C_{2,3} + a_{3,3}C_{3,3}+a_{4,3}C_{4,3} \\ &= 0\cdot C_{1,3} + 0\cdot C_{2,3} + 3\cdot C_{3,3} + 0\cdot C_{4,3}\end{aligned}\end{align} \nonumber \]

Чудова річ тут полягає в тому, що три наші кофактори множаться на\(0\). Ми не будемо турбувати їх обчислення, оскільки вони не сприятимуть визначенню. Таким чином

\[\begin{align}\begin{aligned}\text{det}(A)&=3\cdot C_{3,3} \\ &=3\cdot (-1)^{3+3}\cdot\left|\begin{array}{ccc}{1}&{2}&{9}\\{2}&{-3}&{5}\\{-4}&{1}&{2}\end{array}\right| \\ &=3\cdot (-147)\quad\left(\begin{array}{c}{\text{we computed the determinant of the }3\times 3\text{ matrix}} \\ {\text{without showing our work; it is }-147}\end{array}\right) \\ &=-447\end{aligned}\end{align} \nonumber \]

Вау. Це було набагато простіше, ніж обчислення все, що ми зробили в прикладі 3.3.6. Звичайно, у цьому прикладі у нас не було жодних ярликів, які ми могли б використати.

Приклад\(\PageIndex{2}\)

Знайдіть детермінант

\[A=\left[\begin{array}{ccccc}{1}&{2}&{3}&{4}&{5}\\{0}&{6}&{7}&{8}&{9}\\{0}&{0}&{10}&{11}&{12}\\{0}&{0}&{0}&{13}&{14} \\ {0}&{0}&{0}&{0}&{15}\end{array}\right]. \nonumber \]

Рішення

На перший погляд ми думаємо: «Я не хочу знаходити детермінант\(5\times 5\) матриці!» Однак, використовуючи наші новоотримані знання, ми бачимо, що все не так вже й погано. Насправді ця проблема дуже легка.

Який рядок або стовпець ми повинні вибрати, щоб знайти детермінант уздовж? Є два очевидних варіанти: перший стовпець або останній рядок. Обидва мають в них 4 нулі. Вибираємо перший стовпець. \(^{1}\)Ми опускаємо більшу частину розширення кофактора, оскільки більша його частина є лише\(0\):

\[\text{det}(A)=1\cdot (-1)^{1+1}\cdot\left|\begin{array}{cccc}{6}&{7}&{8}&{9}\\{0}&{10}&{11}&{12}\\{0}&{0}&{13}&{14}\\{0}&{0}&{0}&{15}\end{array}\right|. \nonumber \]

Аналогічно, цей детермінант не погано обчислити; ми знову вирішили використовувати розширення кофактора уздовж першого стовпця. Примітка: технічно це розширення кофактора є\(6\cdot(-1)^{1+1}A_{1,1}\); ми збираємося відмовитися від\((-1)^{1+1}\) умов звідси в цьому прикладі (це буде багато...).

\[\text{det}(A)=1\cdot 6\cdot\left|\begin{array}{ccc}{10}&{11}&{12}\\{0}&{13}&{14}\\{0}&{0}&{15}\end{array}\right|. \nonumber \]

Ви, напевно, можете побачити тенденцію. Ми закінчимо кроки, не пояснюючи кожен з них.

\[\begin{align}\begin{aligned}\text{det}(A)&=1\cdot 6\cdot 10\cdot\left|\begin{array}{cc}{13}&{14}\\{0}&{15}\end{array}\right| \\ &=1\cdot 6\cdot 10\cdot 13\cdot 15 \\ &=11700\end{aligned}\end{align} \nonumber \]

Ми бачимо, що кінцевим визначником є добуток діагональних записів. Це працює для будь-якої трикутної матриці (а оскільки діагональні матриці трикутні, вона працює і для діагональних матриць). Це досить важлива ідея, що ми покладемо її в коробку.

Ключова ідея\(\PageIndex{1}\): The Determinant of Triangular Matrices

Визначником трикутної матриці є добуток її діагональних елементів.

Зараз знову час почати думати, як математик. Пам'ятайте, математики бачать щось нове і часто запитують: «Як це пов'язано з речами, які я вже знаю?» Отже, тепер ми запитуємо: «Якщо ми змінимо матрицю якимось чином, як це детермінант змінився?»

Стандартний спосіб, яким ми змінюємо матриці, - це елементарні операції рядків. Якщо виконати елементарну рядкову операцію над матрицею, як визначник нової матриці буде порівнюватися з визначником вихідної матриці?

Давайте спочатку поекспериментуємо, а потім офіційно заявимо, що відбувається.

Приклад\(\PageIndex{3}\)

Нехай

\[A=\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]. \nonumber \]

\(B\)Дозволяти формуватися з\(A\), виконавши одну з наступних елементарних операцій рядка:

1. \(2R_{1}+R_{2}\to R_{2}\)
2. \(5R_{1}\to R_{1}\)
3. \(R_{1}\leftrightarrow R_{2}\)

Знайти\(\text{det}(A)\) так само, як і\(\text{det}(B)\) для кожної з операцій рядка вище.

Рішення

Це просто обчислити\(\text{det}(A) = -2\).

\(B\)Дозволяти формуватися, виконуючи операцію рядка в 1) на\(A\); таким чином

\[B=\left[\begin{array}{cc}{1}&{2}\\{5}&{8}\end{array}\right]. \nonumber \]

Зрозуміло\(\text{det}(B) = -2\), що, те ж саме, що і\(\text{det}(A)\).

Тепер\(B\) нехай формується, виконуючи елементарну операцію ряду в 2) на\(A\); тобто

\[B=\left[\begin{array}{cc}{5}&{10}\\{3}&{4}\end{array}\right]. \nonumber \]

Ми бачимо\(\text{det}(B) = -10\), що, що є\(5\cdot\text{det}(A)\).

Нарешті, нехай\(B\) буде сформована операція третього рядка задана; поміняти місцями два ряди\(A\). Ми бачимо, що

\[B=\left[\begin{array}{cc}{3}&{4}\\{1}&{2}\end{array}\right] \nonumber \]

і те\(\text{det}(B) = 2\), що є\((-1)\cdot\text{det}(A)\).

Ми бачили в наведеному вище прикладі, що, здається, існує зв'язок між детермінантами матриць «до і після», які змінюються елементарними рядковими операціями. Звичайно, одного прикладу недостатньо, щоб базувати теорію, і ми ще нічого не довели. Незважаючи на це, така теорема вірна.

Теорема\(\PageIndex{2}\)

Визначні та елементарні операції рядків

\(A\)Дозволяти бути\(n\times n\) матрицею і нехай\(B\) утворюються шляхом виконання однієї елементарної операції рядка на\(A\).

1. Якщо\(B\) формується з\(A\) додаванням скалярного кратного одному ряду до іншого, то\(\text{det}(B) = \text{det}(A)\).
2. Якщо\(B\) утворюється від\(A\) множення одного ряду\(A\) на скаляр\(k\), то\(\text{det}(B) = k\cdot\text{det}(A)\).
3. Якщо\(B\) утворюється з\(A\) шляхом перемежування двох рядів\(A\), то\(\text{det}(B) = −\text{det}(A)\).

Давайте поставимо цю теорему для використання в прикладі.

Приклад\(\PageIndex{4}\)

Нехай

\[A=\left[\begin{array}{ccc}{1}&{2}&{1}\\{0}&{1}&{1}\\{1}&{1}&{1}\end{array}\right]. \nonumber \]

Обчислити\(\text{det}(A)\), а потім знайти детермінанти наступних матриць шляхом перевірки за допомогою теореми\(\PageIndex{2}\).

\[B=\left[\begin{array}{ccc}{1}&{1}&{1}\\{1}&{2}&{1}\\{0}&{1}&{1}\end{array}\right]\quad C=\left[\begin{array}{ccc}{1}&{2}&{1}\\{0}&{1}&{1}\\{7}&{7}&{7}\end{array}\right]\quad D=\left[\begin{array}{ccc}{1}&{-1}&{-2}\\{0}&{1}&{1}\\{1}&{1}&{1}\end{array}\right] \nonumber \]

Рішення

Обчислення\(\text{det}(A)\) шляхом розширення кофактора вниз по першому стовпчику або вздовж другого рядка здається найкращим вибором, використовуючи один нуль в матриці. Ми можемо швидко це підтвердити\(\text{det}(A) = 1\).

Щоб обчислити\(\text{det}(B)\), зверніть увагу, що рядки\(A\) були переставлені до форми\(B\). Існують різні способи опису того, що сталося; за словами\(R_1\leftrightarrow R_2\) слідували\(R_1\leftrightarrow R_3\) виробляє\(B\) з\(A\). Так як існували два рядні свопи,\(\text{det}(B) = (-1)(-1)\text{det}(A) = \text{det}(A) = 1\).

Зверніть увагу, що\(C\)\(A\) утворюється від множення третього ряду на\(7\). Таким чином\(\text{det}(C) = 7\cdot\text{det}(A) = 7\).

Це займає трохи роздумів, але ми можемо\(A\) сформуватися\(D\) від операції\(-3R_2+R_1\rightarrow R_1\). Цей тип елементарної операції рядка не змінює детермінант, тому\(\text{det}(D) = \text{det}(A)\).

Давайте продовжуємо думати, як математики; математики, як правило, згадують «проблеми», з якими вони стикалися в минулому, \(^{2}\)і коли вони дізнаються щось нове, вони намагаються застосувати свої нові знання для вирішення своєї старої проблеми.

Яку «проблему» ми нещодавно розкрили? Ми заявляли в останньому розділі, що навіть комп'ютери не могли обчислити детермінант великих матриць з кофакторним розширенням. Як же тоді обчислити детермінант великих матриць?

Щойно ми дізналися два цікавих і корисних факту про матричні детермінанти. По-перше, визначник трикутної матриці легко обчислити: досить помножити діагональні елементи. По-друге, ми знаємо, як елементарні операції рядків впливають на визначник. З'єднайте ці дві ідеї разом: задавши будь-яку квадратну матрицю, ми можемо використовувати елементарні операції рядків, щоб поставити матрицю в трикутну форму, \(^{3}\)знайти детермінант нової матриці (що легко), а потім відрегулювати це число, згадавши, які елементарні операції ми виконали. Давайте практикуємо це.

Приклад\(\PageIndex{5}\)

Знайдіть детермінант,\(A\) попередньо поклавши\(A\) в трикутну форму, де

\[A=\left[\begin{array}{ccc}{2}&{4}&{-2}\\{-1}&{-2}&{5}\\{3}&{2}&{1}\end{array}\right]. \nonumber \]

Рішення

Вводячи\(A\) в трикутну форму, нам не потрібно турбуватися про отримання провідних\(1\) s, але це, як правило, полегшує наше життя, оскільки ми вирішуємо проблему вручну. Отже, давайте масштабуємо перший рядок за допомогою\(1/2\):

\[\frac{1}{2}R_{1}\to R_{1}\quad\left[\begin{array}{ccc}{1}&{2}&{-1}\\{-1}&{-2}&{5}\\{3}&{2}&{1}\end{array}\right]. \nonumber \]

Тепер давайте\(0\) отримаємо нижче цього провідного\(1\):

\[\begin{array}{c}{R_{1}+R_{2}\to R_{2}}\\{-3R_{1}+R_{3}\to R_{3}}\end{array}\quad\left[\begin{array}{ccc}{1}&{2}&{-1}\\{0}&{0}&{4}\\{0}&{-4}&{4}\end{array}\right]. \nonumber \]

Ми можемо закінчити в один крок; міняючи рядки,\(2\) і\(3\) ми будемо мати нашу матрицю в трикутній формі.

\[R_{2}\leftrightarrow R_{3}\quad\left[\begin{array}{ccc}{1}&{2}&{-1}\\{0}&{-4}&{4}\\{0}&{0}&{4}\end{array}\right]. \nonumber \]

Давайте назвемо цю останню матрицю\(B\). Визначник\(B\) легко обчислити, оскільки він трикутний;\(\text{det}(B) = -16\). Ми можемо використовувати це, щоб знайти\(\text{det}(A)\).

Згадайте кроки, в які ми використовували для\(A\) перетворення\(B\). Ними є:

\[\frac 12R_1 \rightarrow R_1 \nonumber \]

\[R_1 + R_2 \rightarrow R_2 \nonumber \]

\[-3R_1+R_3\rightarrow R_3 \nonumber \]

\[R_2 \leftrightarrow R_3 \nonumber \]

Перша операція множимо ряд\(A\) на\(\frac 12\). Це означає, що отримана матриця мала детермінант, який був\(\frac12\) детермінантою\(A\).

Наступні дві операції ніяк не вплинули на визначник. Остання операція, підкачка рядків, змінила знак. Поєднуючи ці ефекти, ми знаємо, що\[-16 = \text{det}(B)= (-1)\frac12\text{det}(A). \nonumber \]

Рішення для\(\text{det}(A)\) нас це є\(\text{det}(A)=32\).

На практиці нам не потрібно відстежувати операції, коли ми додаємо кратні одному рядку до іншого; вони просто не впливають на детермінант. Також на практиці ці кроки виконуються комп'ютером, а комп'ютери не дбають про провідні 1s. Тому операції масштабування рядків використовуються рідко. Єдине, що потрібно відстежувати, - це свопи рядків, і навіть тоді все, що ми дбаємо про це кількість свопів рядків. Непарна кількість рядків свопів означає, що вихідний детермінант має протилежний знак матриці трикутної форми; парна кількість свопів рядків означає, що вони мають однаковий детермінант.

Давайте практикуємо це ще раз.

Приклад\(\PageIndex{6}\)

Матриця\(B\) була сформована з\(A\) використання наступних елементарних рядкових операцій, хоча і не обов'язково в такому порядку. Знайти\(\text{det}(A)\).

\[B=\left[\begin{array}{ccc}{1}&{2}&{3}\\{0}&{4}&{5}\\{0}&{0}&{6}\end{array}\right] \quad\begin{array}{c}{2R_{1}\to R_{1}} \\ {\frac{1}{3}R_{3}\to R_{3}} \\ {R_{1}\leftrightarrow R_{2}} \\ {6R_{1}+R_{2}\to R_{2}}\end{array} \nonumber \]

Рішення

Це легко обчислити\(\text{det}(B)=24\). In looking at our list of elementary row operations, we see that only the first three have an effect on the determinant. Therefore

\[24=\text{det}(B)=2\cdot\frac{1}{3}\cdot (-1)\cdot\text{det}(A) \nonumber \]

і, отже,

\[\text{det}(A)=-36. \nonumber \]

У попередньому прикладі у нас, можливо, виникла спокуса «перебудувати»\(A\) за допомогою елементарних операцій рядків, а потім обчислити детермінант. Це можна зробити, але загалом це погана ідея; це займає занадто багато роботи, і занадто легко помилитися.

Давайте подумаємо, що деякі більше схожі на математика. Як визначник працює з іншими відомими нам матричними операціями? Зокрема, як визначник взаємодіє з додаванням матриць, скалярним множенням, множенням матриць, транспонуванням та слідом? Ми знову зробимо приклад, щоб отримати уявлення про те, що відбувається, а потім дати теорему, щоб заявити, що правда.

Приклад\(\PageIndex{7}\)

Нехай

\[A=\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]\quad\text{and}\quad B=\left[\begin{array}{cc}{2}&{1}\\{3}&{5}\end{array}\right]. \nonumber \]

Знайдіть детермінанти матриць\(A\),\(B\),\(A + B\),\(3A\),\(AB\)\(A^{T}\)\(A^{−1}\), і порівняйте детермінант цих матриць з їх слідом.

Рішення

Ми можемо швидко обчислити, що\(\text{det}(A) = -2\) і те\(\text{det}(B) = 7\).

\[\begin{align}\begin{aligned}\text{det}(A-B)&=\text{det}\left(\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]-\left[\begin{array}{cc}{2}&{1}\\{3}&{5}\end{array}\right]\right) \\ &=\left|\begin{array}{cc}{-1}&{1}\\{0}&{-1}\end{array}\right| \\ &=1\end{aligned}\end{align} \nonumber \]

Важко знайти зв'язок між\(\text{det}(A-b)\),\(\text{det}(A)\) і\(\text{det}(B)\).

\[\begin{align}\begin{aligned}\text{det}(3A)&=\left|\begin{array}{cc}{3}&{6}\\{9}&{12}\end{array}\right| \\ &=-18\end{aligned}\end{align} \nonumber \]

Ми можемо зрозуміти це; множення одного рядка\(A\) на\(3\) збільшує детермінант на коефіцієнт\(3\); роблячи це знову (і, отже, множення обох рядків на\(3\)) збільшує детермінант знову на коефіцієнт\(3\). \(\text{det}(3A)=3\cdot 3\cdot\text{det}(A)\)Тому або\(3^{2}\cdot A\).

\[\begin{align}\begin{aligned}\text{det}(AB)&=\text{det}\left(\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]\left[\begin{array}{cc}{2}&{1}\\{3}&{5}\end{array}\right]\right) \\ &=\left|\begin{array}{cc}{8}&{11}\\{18}&{23}\end{array}\right| \\ &=-14\end{aligned}\end{align} \nonumber \]

Це здається зрозумілим;\(\text{det}(AB)=\text{det}(A)\text{det}(B)\).

\[\begin{align}\begin{aligned}\text{det}(A^{T})&=\left|\begin{array}{cc}{1}&{3}\\{2}&{4}\end{array}\right| \\ &=-2\end{aligned}\end{align} \nonumber \]

Очевидно\(\text{det}(A^{T})=\text{det}(A)\); чи завжди це буде так? Якщо задуматися, то можна побачити, що розширення кофактора вздовж першого ряду\(A\) дасть нам такий же результат, як розширення кофактора уздовж першого стовпця\(A\). \(^{4}\)

\[\begin{align}\begin{aligned}\text{det}(A^{-1})&=\left|\begin{array}{cc}{-2}&{1}\\{3/2}&{-1/2}\end{array}\right| \\ &=1-3/2 \\ &=-1/2\end{aligned}\end{align} \nonumber \]

Здається, ніби

\[\text{det}(A^{-1})=\frac{1}{\text{det}(A)}. \nonumber \]

Ми закінчуємо тим, що, здається, немає ніякого зв'язку між слідом матриці та її детермінантою. Ми залишаємо читачеві обчислити слід для деяких з перерахованих вище матриць і підтвердити це твердження.

Тепер ми викладемо теорему, яка підтвердить наші припущення з попереднього прикладу.

Теорема\(\PageIndex{3}\)

Властивості детермінанти

\(A\)\(B\)Дозволяти і бути\(n\times n\) матриці і нехай\(k\) бути скалер. Вірно наступне:

1. \(\text{det}(kA)=k^{n}\cdot\text{det}(A)\)
2. \(\text{det}(A^{T})=\text{det}(A)\)
3. \(\text{det}(AB)=\text{det}(A)\text{det}(B)\)
4. Якщо\(A\) оборотний, то
   \[\text{det}(A^{-1})=\frac{1}{\text{det}(A)}.\nonumber \]
5. Матриця\(A\) обертається тоді і тільки тоді, коли\(\text{det}(A)\neq 0\).

Це останнє твердження вищезгаданої теореми є значущим: що станеться, якщо\(\text{det}(A) = 0\)? Здається\(\text{det}(A^{-1})="1/0"\), що не визначено. Тут насправді немає проблеми; виявляється, що якщо\(\text{det}(A)=0\), то не\(A\) є зворотним (отже, частина 5 Теореми\(\PageIndex{3}\)). Це дозволяє нам додати до нашої теореми про оборотну матрицю.

Теорема\(\PageIndex{4}\)

Теорема про оборотну матрицю

\(A\)Дозволяти бути\(n\times n\) матрицею. Наступні твердження рівнозначні.

1. \(A\)є оборотним.
2. \(\text{det}(A)\neq 0\).

Це нове доповнення до теореми про інвертабельну матрицю є дуже корисним; ми повернемося до нього в розділі 4, коли ми обговорюємо власні значення.

Закінчуємо цей розділ ярликом для обчислення детермінант\(3\times 3\) матриць. Розглянемо матрицю\(A\):

\[\left[\begin{array}{ccc}{1}&{2}&{3}\\{4}&{5}&{6}\\{7}&{8}&{9}\end{array}\right]. \nonumber \]

Ми можемо обчислити його детермінант за допомогою кофакторного розширення, як ми це робили в прикладі 3.3.4. Після того, як хтось стає досвідченим у цьому методі, обчислення\(3\times3\) визначника a не все так важко. Однак спосіб, який багато хто вважає простішим, починається з перезапису матриці без дужок і повторення першого і другого стовпців в кінці, як показано нижче. \[\begin{array}{ccccc} 1&2&3&1&2 \\ 4 & 5 & 6&4&5\\7&8&9&7&8\end{array} \nonumber \]

У цьому\(3\times 5\) масиві чисел є 3 повні діагоналі «від верхнього лівого до нижнього правого» та 3 повних діагоналі «верхнього правого нижнього лівого», як показано нижче зі стрілками.

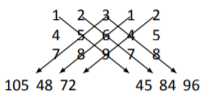
Числа, які з'являються на кінцях кожної зі стрілок, обчислюються шляхом множення знайдених по стрілках цифр. Наприклад,\(105\) походить від множення\(3\cdot5\cdot7=105\). Визначник знаходять шляхом складання чисел праворуч, і віднімання суми чисел зліва. Тобто,\[\text{det}(A) = (45+84+96) - (105+48+72) = 0. \nonumber \]

Щоб нагадати собі цей ярлик, ми зробимо його ключовою ідеєю.

Ключова ідея\(\PageIndex{2}\): \(3\times 3\) Determinant Shortcut

\(A\)Дозволяти бути\(3\times 3\) матрицею. Створіть\(3\times 5\) масив, повторюючи перші\(2\) стовпці і розгляньте добутки діагоналей\(3\) «правої руки» і діагоналей\(3\) «лівої руки», як показано раніше. Тоді

\[\begin{align}\begin{aligned}\text{det}(A)&=\text{"(the sum of the right hand numbers)} \\ & -\text{(the sum of the left hand numbers)".}\end{aligned}\end{align} \nonumber \]

Ми ще раз попрактикуємося в контексті прикладу.

Приклад\(\PageIndex{8}\)

Знайти визначник\(A\) використання раніше описаного ярлика, де

\[A=\left[\begin{array}{ccc}{1}&{3}&{9}\\{-2}&{3}&{4}\\{-5}&{7}&{2}\end{array}\right]. \nonumber \]

Рішення

Переписування першого\(2\) columns, drawing the proper diagonals, and multiplying, we get:

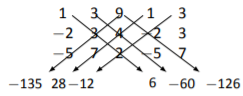
Підсумовуючи числа праворуч і віднімаючи суму чисел зліва, отримуємо\[\text{det}(A) = (6-60-126) - ( -135+28-12) = -61. \nonumber \]

In the next section we’ll see how the determinant can be used to solve systems of linear equations.

Footnotes

[1] We do not choose this because it is the better choice; both options are good. We simply had to make a choice.

[2] which is why mathematicians rarely smile: they are remembering their problems

[3] or echelon form

[4] This can be a bit tricky to think out in your head. Try it with a 3\(\times 3\) matrix \(A\) and see how it works. All the \(2\times 2\) submatrices that are created in \(A^{T}\) are the transpose of those found in \(A\); this doesn’t matter since it is easy to see that the determinant isn’t affected by the transpose in a \(2\times 2\) matrix.